Arrays and Area Models to The Standard Algorithm

Did you know that the words “array” and “area model” appear in the Grade 1-8 Math Curriculum a combined 22 times?

Not only do arrays and area models help to support the development of proportional reasoning when we formally introduce multiplication in primary, but they also help us understand how to develop strategies that lead to building number flexibility and the automaticity of math facts.

Arrays and area models should be used as a tool and representation for many big ideas in mathematics including, but not limited to:

• Multiplication
• Distributive Property with Whole Numbers
• Finding Area with Whole Number Dimensions
• Perfect Squares & Square Roots
• Multiplying a Binomial by Monomial
• Multiplying a Binomial by Binomial (aka FOIL)
• Factoring (Common, Simple/Complex Trinomials)
• Completing the Square

For many, the term “array” is not a familiar one. Luckily, the definition is fairly straightforward:

In mathematics, an array is a group of objects ordered in rows and columns.

Seems pretty simple, but they are extremely powerful in building a deep conceptual understanding as students learn multiplication and begin applying that knowledge to more abstract ideas requiring fluency with procedures.

Where Multiplication Begins In The Ontario Curriculum

In grade 3, students are asked to:

• relate multiplication of one-digit numbers and division by one-digit divisors to real life situations, using a variety of tools and strategies (e.g., place objects in equal groups, use arrays, write repeated addition or subtraction sentences);
• multiply to 7 x 7 and divide to 49 ÷ 7, using a variety of mental strategies (e.g., doubles, doubles plus another set, skip counting);
• identify, through investigation, the properties of zero and one in multiplication (i.e., any number multiplied by zero equals zero; any number multiplied by 1 equals the original number) (Sample problem: Use tiles to create arrays that represent 3 x 3, 3 x 2, 3 x 1, and 3 x 0. Explain what you think will happen when you multiply any number by 1, and when you multiply any number by 0.);

Consider 3 x 2, or “3 groups of 2”:

This may seem like a simple and maybe even unnecessary representation, but having a visual that multiplying two numbers will always yield a rectangular array is an important concept that not only shows the interconnectedness of the Number Sense and Numeration strand to Measurement, but also implicitly provides students with insight into why more abstract mathematics works later on in grade 9 and 10.

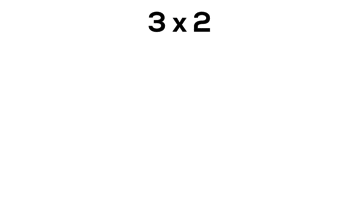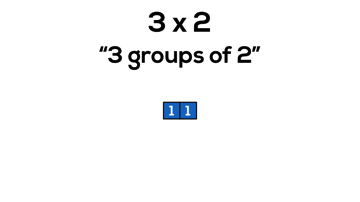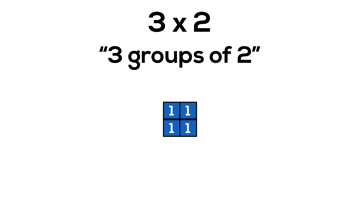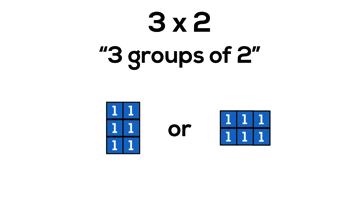
In grade 3, it is reasonable to believe that students are still working on counting and quantity including unitizing in order to skip count more fluently. By working with arrays, we can allow students to continue developing their ability to unitize and work with composing and decomposing numbers.

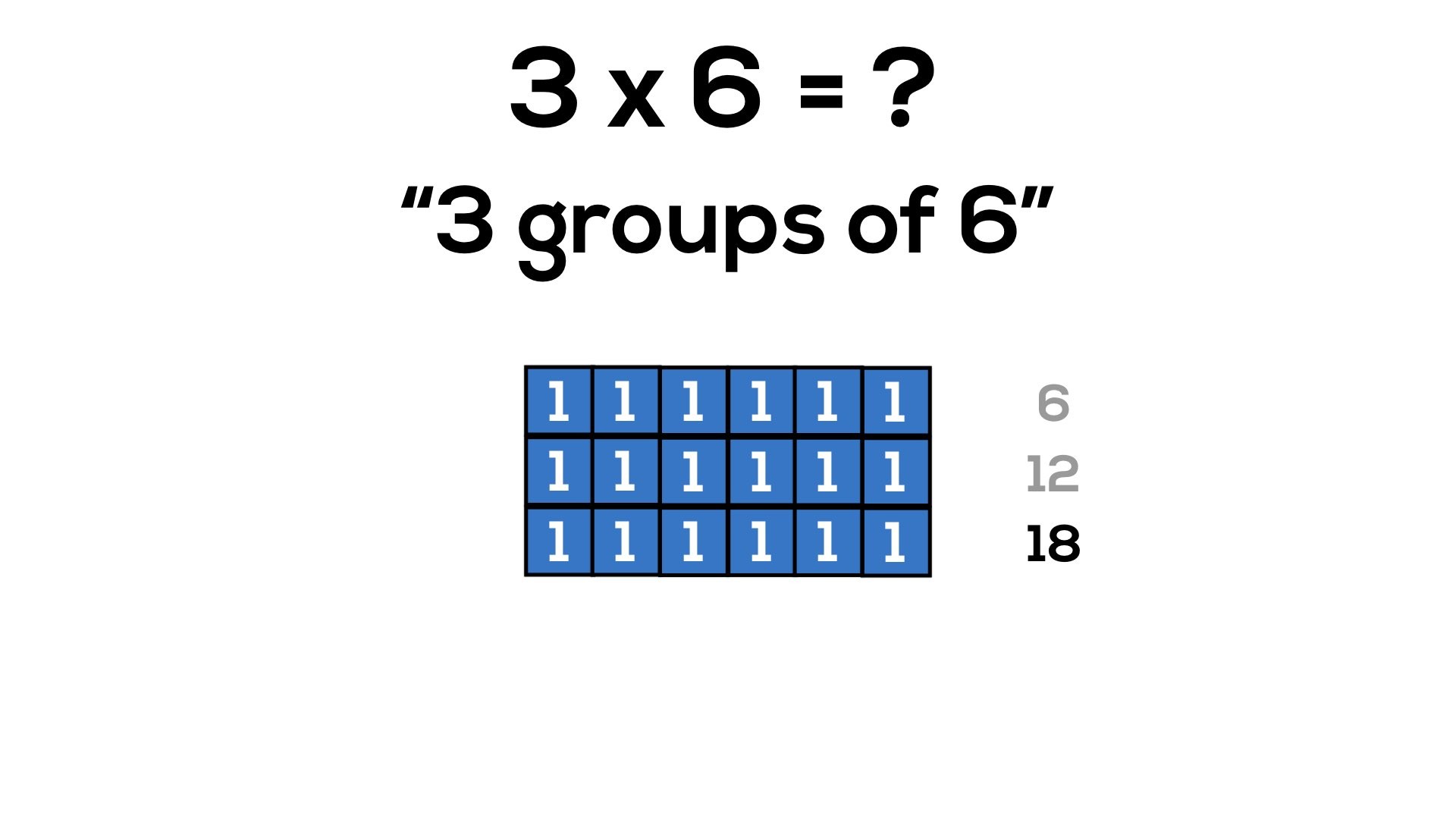
Arrays and Perfect Squares

Not only is it beneficial for students to understand that multiplying two quantities will yield an array covering a rectangular area, but it is also useful for students to discover without explicitly stating that when we make an array where the number of groups and number of items in each group are equal, the array is now a special rectangle; a square!

While we don’t specifically discuss perfect squares until intermediate when students represent perfect squares and square roots using a variety of tools in grade 7 and estimate/verify the positive square roots of whole numbers in grade 8, I think it would be much easier for students to identify a perfect square and estimate the square root of a number if they have four years of concrete and visual work with perfect squares.

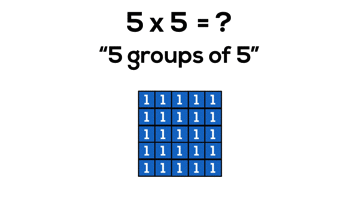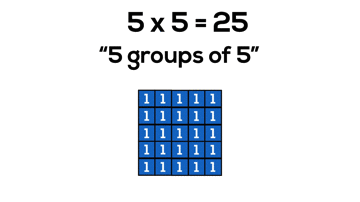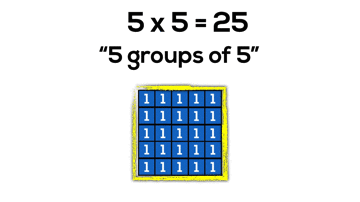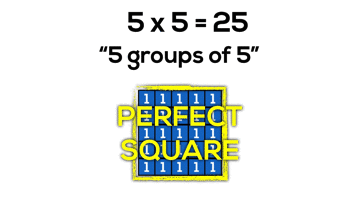
How Multiplication With Arrays Lead to Area

As we have witnessed in the previous examples, with every array a student builds, we are implicitly providing them with a window into the measurement strand with opportunities to think about perimeter and area. Not only can we easily make connections between an array and the area of a rectangle, but we can also better serve specific expectations involving estimation such as this grade 3 Measurement expectation:

• estimate, measure (i.e., using centimetre grid paper, arrays), and record area.

With the use of arrays in the Number Sense and Numeration strand, I can better serve my Measurement strand with problems that force students to estimate using visuals and then improve their predictions using concrete manipulatives.

Something worth noting is the wording of the specific expectation in the grade 3 curriculum related to multiplication and division which states students are to multiply to 7 x 7 and divide to 49 ÷ 7, using a variety of mental strategies without any reference to memorization or automaticity. While I agree that knowing multiplication tables for intermediate and senior level math courses is a huge asset, I think working with multiplication early and often with concrete manipulatives is a great way to get there over other more traditional and/or rote strategies.

Multiplying Larger Numbers – Creating a Need To Chunk

When students enter grade 4, we extend our multiplication and division through the use of a variety of mental strategies to multiplying to 9 x 9 and dividing to 81 ÷ 9. As the factors and divisors get larger, we begin creating a need for some new strategies that will help us as we approach two-digit multiplication. In the grade 4 Patterning and Algebra strand, students are expected to:

• identify, through investigation (e.g., by using sets of objects in arrays, by drawing area models), and use the distributive property of multiplication over addition to facilitate computation with whole numbers (e.g.,“I know that 9 x 52 equals 9 x 50 + 9 x 2. This is easier to calculate in my head because I get 450 + 18 = 468.”).

Sounds kind of complicated. Ultimately, what the distributive property is trying to offer students is a way to “chunk” their factors into friendlier numbers to make multiplication easier.

Let’s have a look at a basic example:

If a student does not know how many objects there are in six groups of seven, they can use distributive property to “chunk” this multiplication problem into two or more smaller multiplication problems and add the products. In the example above, the student may have a comfort with multiples of 5. In the example below, the student might like working with 5 groups of 5 because the product, 25, is a friendly number to add up afterwards.

Although not explicitly stated in the grade 4 curriculum, I think it is worth noting that the introduction of the distributive property is the first situation where a bracket could be used symbolically in a mathematical expression:

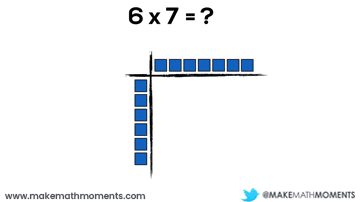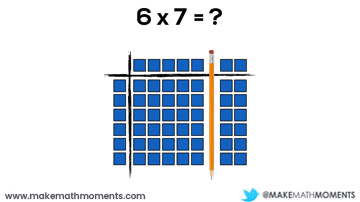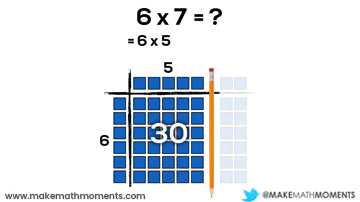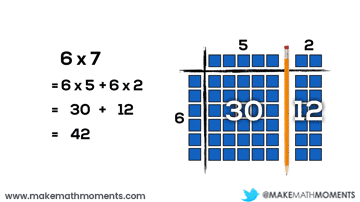
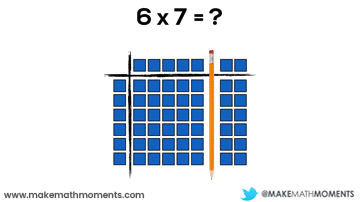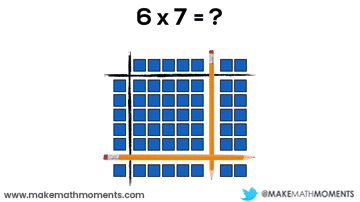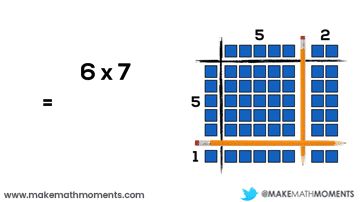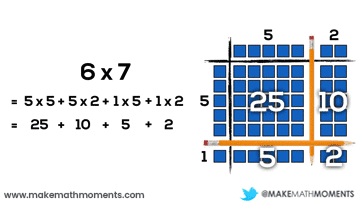
6 x 7
= 6(5 + 2)

or

6 x 7
= 5(5 + 2) + 1(5 + 2)

While a bracket could be used symbolically, I don’t think it would be developmentally appropriate or useful. However, when brackets do show up on the scene later on, how awesome would it be to connect them to our prior knowledge of arrays and distributive property?

Base Ten Blocks – Making Two-Digit Multiplication Easier

In grade 5, we continue to promote the use of mental strategies for addition, subtraction, and multiplication:

• solve problems involving the addition, subtraction, and multiplication of whole numbers, using a variety of mental strategies (e.g., use the commutative property: 5 x 18 x 2 = 5 x 2 x 18, which gives 10 x 18 = 180);

However, we also move towards finding more efficient ways to multiply factors greater than 9:

• multiply two-digit whole numbers by two-digit whole numbers, using estimation, student-generated algorithms, and standard algorithms;

Unfortunately, I think it is more common for educators to miss the first expectation about mental strategies as well as a huge portion of the second expectation, and rush straight for the standard algorithm.

By continuing to use our knowledge of the distributive property with two-digit by two-digit multiplication, we can begin making things super friendly by splitting our arrays into chunks of 10. However, it can take a whole lot of square tiles and a whole lot of time:

That’s where base ten blocks come in!

What a genius idea to respect the theory of concreteness fading and allow students to begin this new layer of abstraction with the aide of concrete manipulatives to build a deep conceptual understanding.

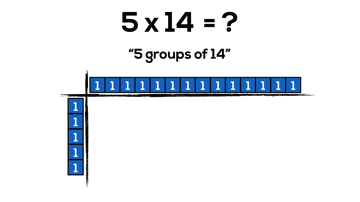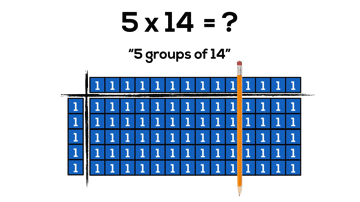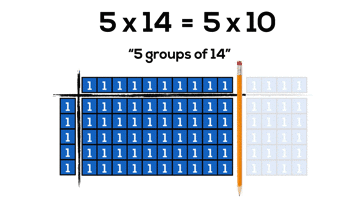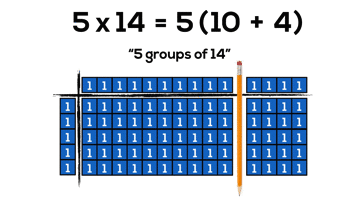
Now, we can do the same problem with much less concrete “pieces”, but still gain all the benefits of manipulatives. Also, how cool is it that base ten blocks are what I call “forced distribution” into chunks of friendly 10’s.

As we introduce base ten blocks, we also begin to transition more explicitly from an array to an area model. Since we are no longer using single tiles to represent each single object or unit of an array, the “ten rods” and “hundred flats” are covering areas of 10 units-squared and 100 units-squared, respectively.

The fun doesn’t stop here. Multiplying two-digit by two-digit numbers is extremely helpful using an area model with base ten blocks:

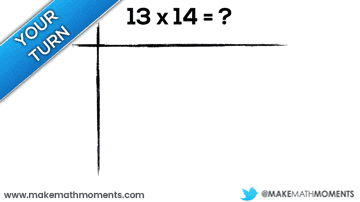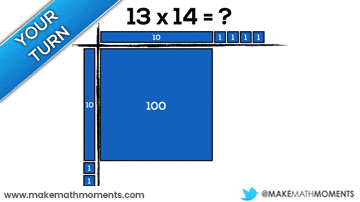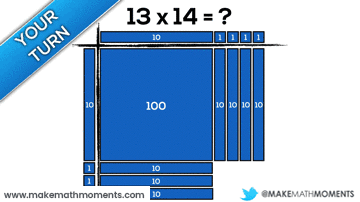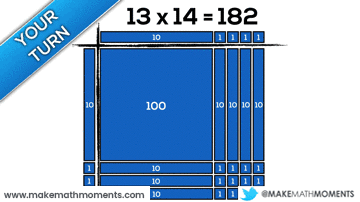
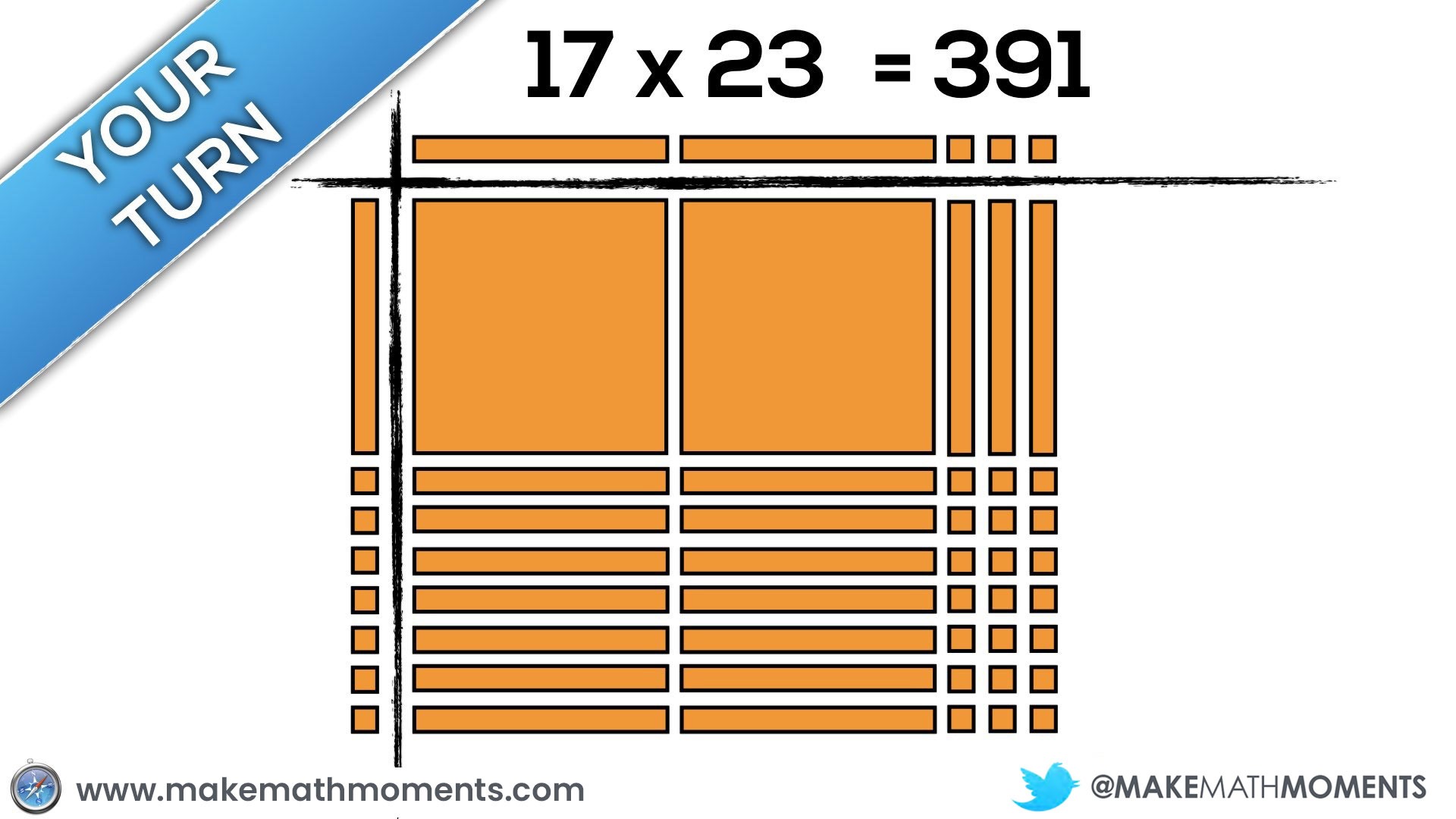
Connecting Arrays & Area Models to the Standard Algorithm

Speaking from experience as a math teacher in my own classroom in Ontario and having an opportunity to travel to observe in classrooms both near and far, I see a common trait where we rush to the algorithm. This race to the procedure might be motivated by teacher beliefs, the anxiety we feel due to limited time and a thick curriculum, or simply a lack of awareness to other approaches and strategies. In any case, I think using arrays and area models can serve as a great precursor to promoting students to begin creating their own algorithms and eventually, connect to the standard algorithm.

Let’s make some connections between the standard algorithm and using arrays and area models.

Consider 22 x 26 using the standard algorithm for multiplication:

While there are many educators who do a great job of breaking the standard algorithm down into its working parts including doing their best to explain the impact place value has on each step to build a conceptual understanding, I think students who can use arrays and area models to multiply have an advantage to building a deeper conceptual understanding.

If using arrays, area models and base ten blocks for multiplication is a new idea for you, then it might be worth making some connections between these representations and the standard algorithm.

Have a look at the area model representation and the standard algorithm method for 22 x 26.

Can you make any connections between the two representations/methods?

What did you come up with?

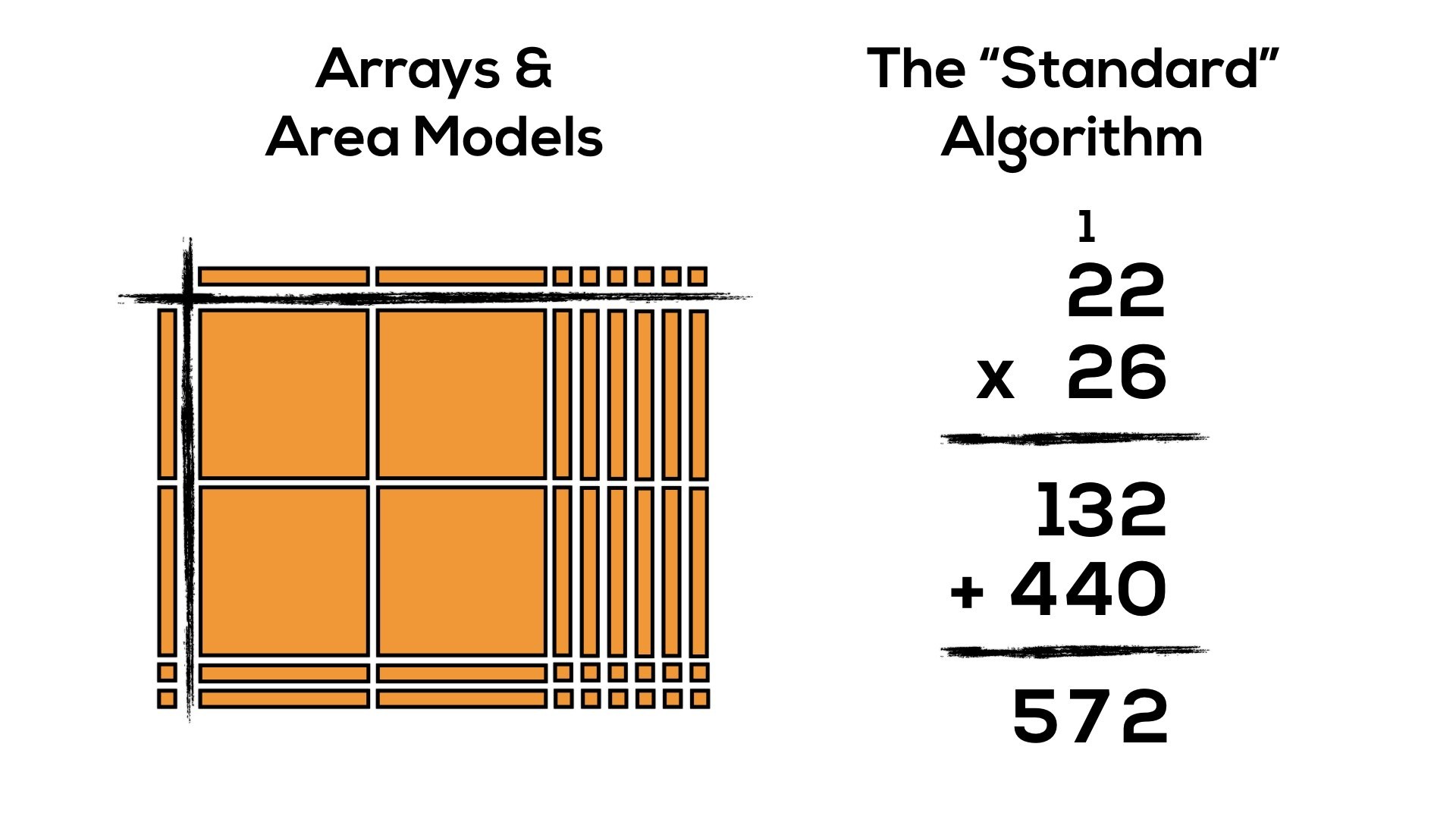
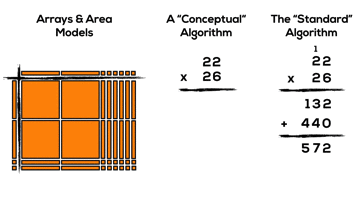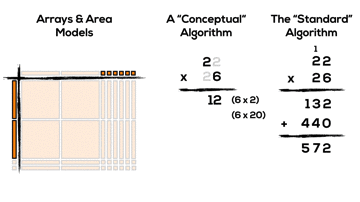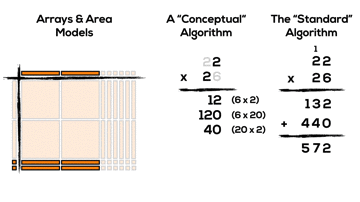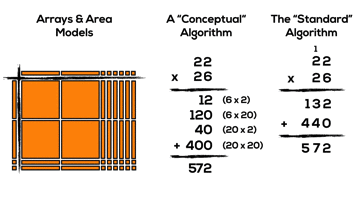
It might not be super obvious, but if we consider the two products created using the algorithm (132 and 440), we can see these products by looking vertically down the area model:

Some might assume that because we end up with two products that the standard algorithm uses distribution to chunk the multiplication of 22 x 26 into two sets of factors. However, if we dig deeper, we will notice that both products are the result of two smaller chunks.

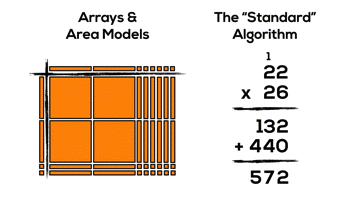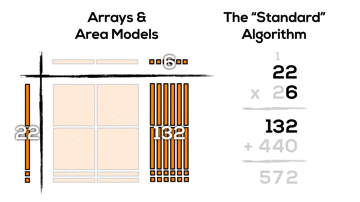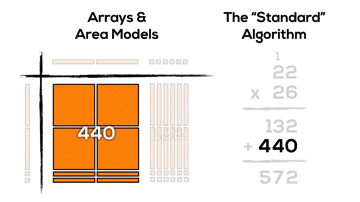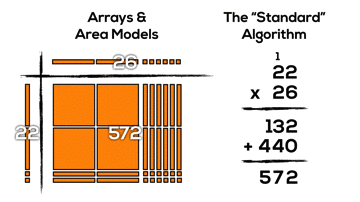
When multiplying two-digit by two-digit factors with the standard algorithm, our base ten place value system allows for chunking into smaller “chunks”:

• x units of 1 times x units of 1
• x units of 1 times x units of 10
• x units of 10 times x units of 1
• x units of 10 times x units of 10

In this case, the standard algorithm breaks up 22 x 26 using the distributive property into the following smaller factors:

• 6 units of 1 times 2 units of 1; (6 x 2)
• 6 units of 1 times 2 units of 10; (6 x 20)
• 2 units of 10 times 2 units of 1; (20 x 2)
• 2 units of 10 times 2 units of 10; (20 x 20)

A “Conceptual” Algorithm Before the “Standard” Algorithm

If we consider all of the deep thinking required to understand how the standard algorithm works conceptually, it might make sense to make the connections more explicit. Let’s come back to the grade 5 expectation multiply two-digit whole numbers by two-digit whole numbers, using estimation, student-generated algorithms, and standard algorithms. Note that student-generated algorithms sits in there and often times, we don’t provide enough opportunities for students to truly create their own strategies and procedures.

Rather than using arrays and area models and then suddenly flying into the standard algorithm, what if we tried to guide students to develop their own “conceptual” algorithm by having them organize the smaller products they are creating when using base ten blocks?

Consider this “conceptual” algorithm that might assist students in making the leap to the standard algorithm when developmentally appropriate:

The connections don’t stop here, either. By explicitly addressing the conceptual understandings behind why the standard algorithm works, students can then apply that same thinking to create their own friendly chunks outside of those limited to 10s created when using base ten blocks.

The Standard Algorithm is the Same As Multiplying Two Binomials

You may recall the acronym “FOIL” which is commonly used for students to remember how to multiply two binomials. While I am guilty for teaching this memorization tool in my math class until only a few years ago, I now understand that using tricks like “FOIL” to teach important math concepts is not helpful (and maybe even harmful).

What if instead of simply teaching students “FOIL” or “double-distribution”, which is a skill limited to the very specific case of multiplying two polynomials with two terms, we actually helped students to visualize what multiplying binomials really looks like?

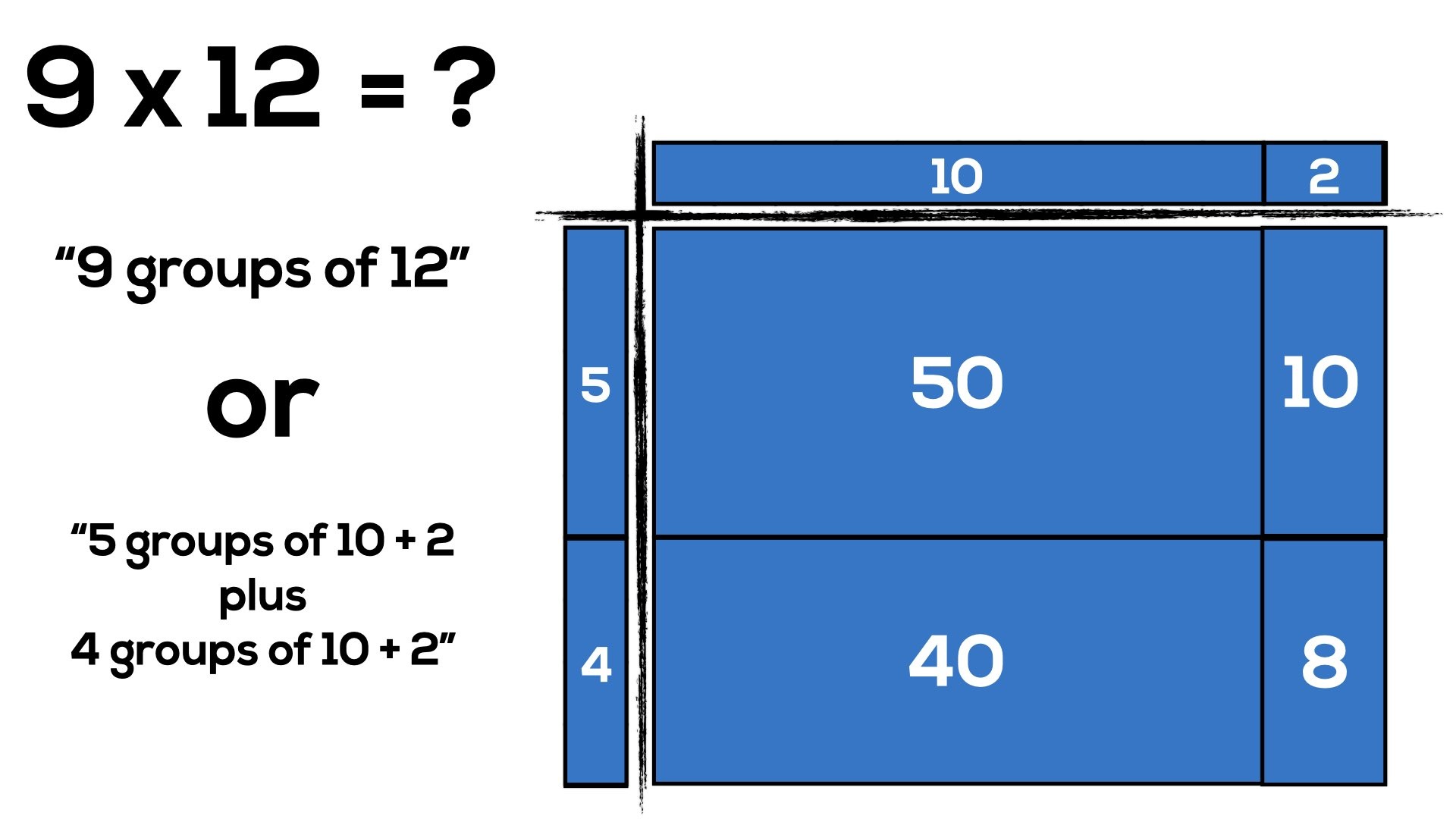
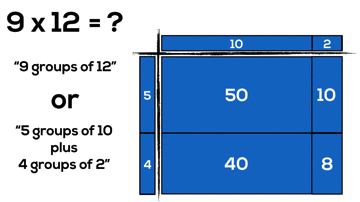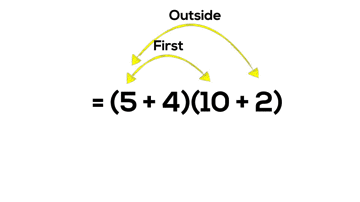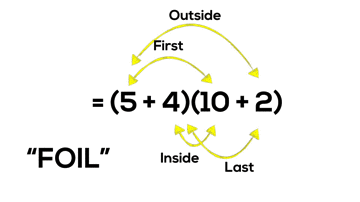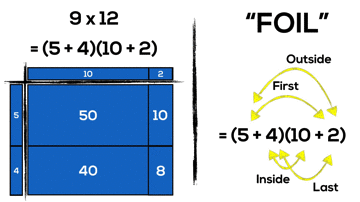
What we see in the previous example is:

9 x 12
= (5 + 4)(10 + 2)
= 5 x 10 + 5 x 2 + 4 x 10 + 4 x 2
= 50 + 10 + 40 + 8
= 108

It might not be obvious to those who have never worked to make a connection, but what the standard algorithm we teach in grade 5 is actually the same procedure we teach students when multiplying binomials in grade 10.

As we head into grade 9 and 10, the thinking becomes more abstract due to the use of variables.

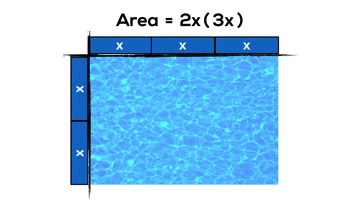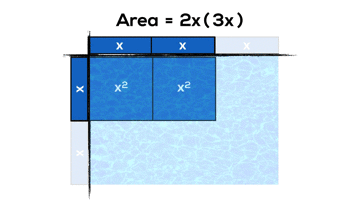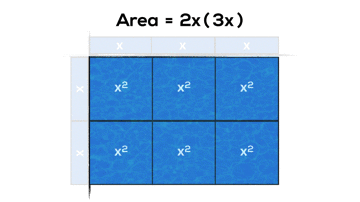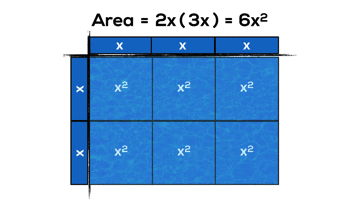
Some Expectations from Grade 9 Academic:

• multiply a polynomial by a monomial involving the same variable [e.g., 2x(x + 4), 2x^2(3x^2 – 2x + 1)], using a variety of tools (e.g., algebra tiles, diagrams, computer algebra systems, paper and pencil);
• expand and simplify polynomial expressions involving one variable [e.g., 2x(4x + 1) – 3x(x + 2)], using a variety of tools (e.g., algebra tiles, computer algebra systems, paper and pencil);

And here’s a couple examples of what these might look like if we use arrays and area models from grade 3 onwards:

An Expectation from Grade 10 Academic:

• expand and simplify second-degree polynomial expressions [e.g., (2x + 5)^2,
  (2x – y)(x + 3y)], using a variety of tools (e.g., algebra tiles, diagrams, computer algebra systems, paper and pencil) and strategies (e.g., patterning);

Here’s an example of what this might look like:

If we are helping students understand what math looks like whenever and wherever possible as I have tried to do in this post for the progression of multiplication, then it would seem logical that some of these quite challenging expectations would be much less complex if we use arrays and area models prior to rushing to the algorithm.

How are you learning in order to better understand what math looks like concretely and visually?

Be sure to check out our problem based multiplication lessons to teach through task so all students can access rich mathematical experiences!