The Make Math Moments 3-Part Framework Guidebook
Spark Curiosity, Fuel Sense-Making, and Ignite Teacher Moves!
How do you create a culture of engagement and participation in your math class to ensure students are leaning in to learn?
Then, once students are leaning in, how are we going to tackle new mathematical ideas in a way that builds the necessary conceptual understanding and develops procedural fluency over time?
Finally, how can we craft our lessons in such a way that every student can access the mathematical content and don’t throw their arms up in frustration?
We believe that all of the above are important parts of an effective mathematics lesson, but successfully delivering lessons that deliver on all of them is not always an easy task.
That’s why we came up with the Make Math Moments 3-Part Framework to deliver math lessons that students will not only love, but will learn from.
So what is the Make Math Moments 3-Part Framework and how can you use it to design your lessons? Well, it is going to require that we rethink our understanding of how students learn and how we teach mathematics.
It might help to first reflect on how you remember learning mathematics in school.
How we remember math class…
For almost a decade, we taught our math lessons exactly the way we were taught using a gradual release of responsibility model using an “I do, we do, you do” approach. These lessons would often be structured like this:
- Take up homework
- Teacher led note giving definitions, formulas, algorithms, steps, and procedures
- Teacher led examples
- Practice time both in-class and/or at home
While there is research showing that students can perform well on assessments by following the gradual release of responsibility model, more research is being done to analyze whether students are truly learning or simply mimicking what the teacher is doing through memorization.
Peter Liljedahl – our guest from episode 21 of the podcast – is one of many researchers who is exploring this idea of mimicking whether this approach is as effective a teaching strategy as we might think.
In research conducted by Liljedahl with a class of 29 students, it was found that teaching students through direct instruction and worked examples prior to students attempting similar problems led to over half of students simply mimicking the steps and procedures teachers used in the lesson and examples while another 20% or so of the class engaging in behaviours characterised as faking (i.e.: making it look like they were working on the problem) or stalling (i.e.: using strategies to intentionally avoid doing the work).
Approximately 20% of the students in that particular class were found to actually be engaged in the behaviour characterised as reasoning.
The right side of this visual by Laura Wheeler does a fantastic job showing the results of this particular case study:
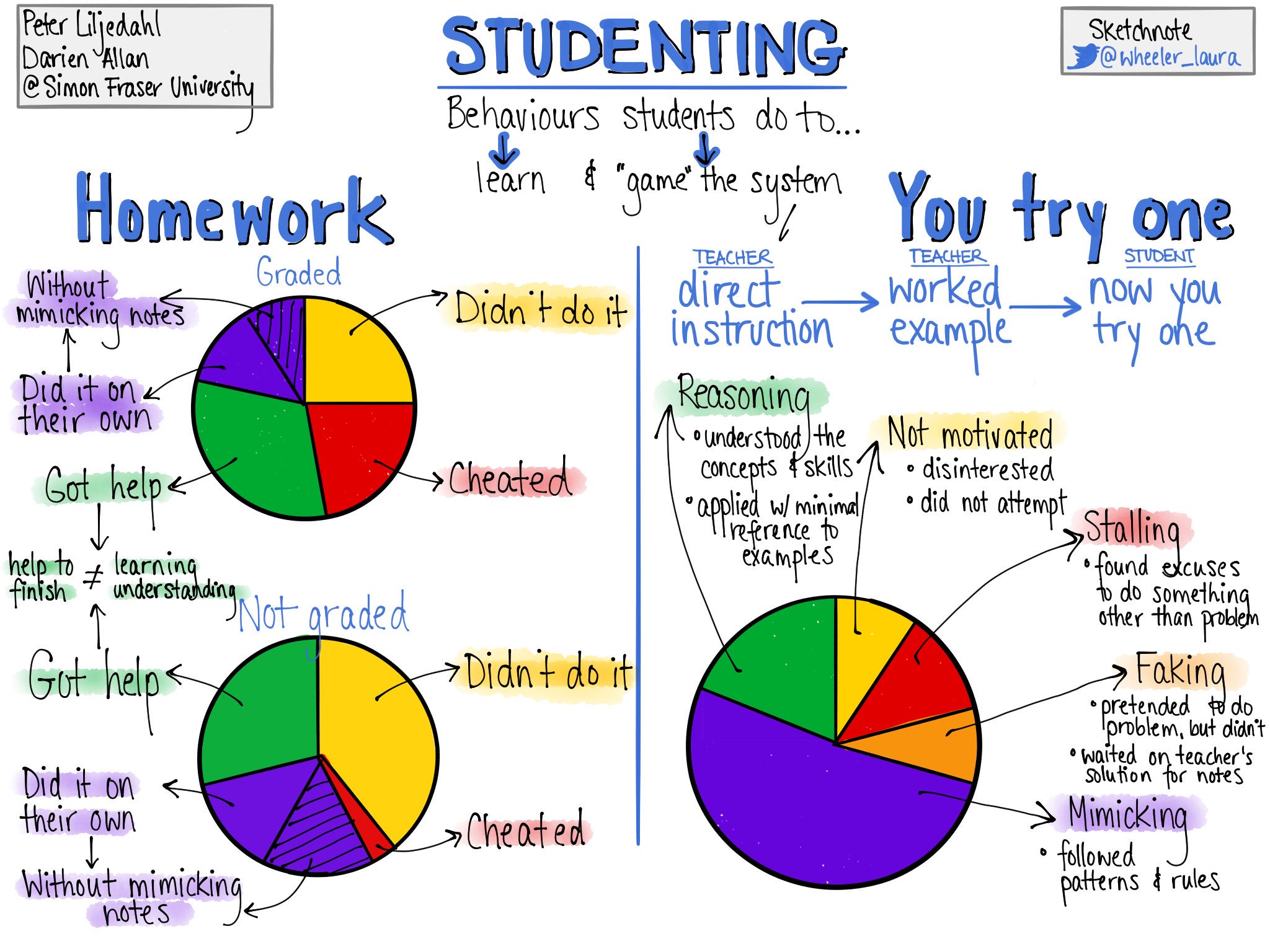



- student interest and engagement;
- student-led sense-making; and,
- productive struggle.
After years of leading presentations, workshops, and keynotes, we knew we had to refine what was working for us into a model that could be easily understood and replicated in any classroom from kindergarten through grade 12.
So, we flipped the script on our traditional math class teaching model and created the Make Math Moments 3-Part Framework to assist all teachers in promoting resilient problem solvers through productive struggle in their classrooms each and every day.
The Make Math Moments Framework can be broken down into these three (3) big components that are tightly connected and even intertwined:
- Sparking curiosity
- Fuelling sense-making
- Igniting teacher moves


Part 1: Sparking Curiosity

We think that engagement is one of the most overused, yet least understood concepts in education.
What is engagement, anyway?
How can we measure whether students are engaged in our math lesson?
Is it enough to say students are engaged if they are staring at us intently without any noticeable distractions?
For many years, that’s exactly what we thought. But now, we’re not convinced.
We don’t just want students “paying attention” or behaviourally engaged. We want students to become actively involved in the lesson, noticing and wondering, sharing their thoughts, and offering predictions and estimates.
We want students intellectually and cognitively engaged in our math class.
It’s been a real challenge, but after years of trying to figure out ways of better engaging our classes, we slowly started putting key pieces together to make that happen more consistently in our classrooms.
And it all started with Dan Meyer’s Three Acts of a Mathematical Story:

Image from Dan Meyer’s blog post: The Three Acts Of A Mathematical Story
We tinkered with our own 3 act math tasks for a number of years, saw the positive reaction we got from our students, and examples from other teachers.
We saw a ton of variety in how these 3 act math tasks were being implemented and continued to learn, making some errors and improvements along the way and learning what did and didn’t work as well.
These are things we want to help you avoid, whether it’s a particular tool that we think works best or a routine that can help your lessons fly instead of flop.
And along the way, for each technique, we’ll offer examples and show how we implemented each technique in a lesson.
But before we do that, let’s talk a bit about one of the keys we realized about how we were implementing 3 act math tasks and how it made all the difference in terms of sparking curiosity and engagement in class.
The power of storytelling
We really struggled for a long time to build the understanding and skill necessary to facilitate a problem based lesson without a hitch.
We missed the importance of using elements of storytelling within our three-act math tasks and why Dan explains them in the form of a kind of “mathematical story”.
However, learning the importance of this through experience and reflection, as well as how to implement these problem based lessons more effectively, made all the difference.
You might think, “Kyle/Jon, what does storytelling have to do with teaching math?”
Well, it turns out, a lot.
A good story presents a bit of information in the beginning – clues, glimmers of something – which gets you to start noticing, wondering, and asking questions.
You don’t have all the necessary information yet and because of this, now you’re dying to know the answer.
On his blog, author and screenwriter Steven Pressfield (writer of The Legend of Bagger Vance among others) talks about the three act structure and how it can be applied to virtually any story (even things we don’t typically think of as stories).
He uses the example of Herman Melville’s classic novel Moby Dick:


A good math lesson that sparks curiosity is structured in a similar way.
In the beginning during Act 1, you want to give your students sufficient motivation to set out or “pursue” the problem. So, you withhold information and create anticipation with something like a video, an interesting image, or even a context storyline through spoken word.
It is during this time when you encourage student voice to come through by sharing their noticings and wonderings. The discourse and community building that takes place during this phase of a lesson is so important and necessary to build a non-threatening classroom environment.
Every voice matters. Every student matters.
Then, during the beginning of Act 2, we land on a wonder that we are going to explore further.
Students are given an opportunity to make predictions and/or estimates based on what they know so far and share them out to their partners and/or groups before sharing with the class as a whole.
Students are now ready to begin a productive struggle through problem solving.
We then slowly reveal more information that has been strategically planned to promote students utilizing prior knowledge with new concepts, models, and strategies just out of reach as they attempt to build off of their initial estimates into more precise calculations.
It is during this time that teachers are monitoring, selecting, and sequencing student work while posing purposeful questions in order to promote student reasoning without robbing them of their own thinking. This is where the fuelling of sense-making lives in a math classroom where students are pushed to productively struggle through the problem solving process.
As students work collaboratively in small groups and checking in with other groups to seek clarification, a different perspective, or a nudge to push thinking forward, we get closer to the consolidation of the lesson where we (the teacher) elicit student thinking and begin making connections amongst the strategies, tools, and representations students used to solve the problem.
At the end of the consolidation, the hope is that all students are convinced and agree upon what the class has landed on as a “reasonable” solution.
If that wasn’t fun enough, in Act 3, it’s time for the resolution.
How did their original predictions and/or estimates hold up?
They’ll get the chance to “see it” happen and celebrate when their solution comes extremely close and even exactly matches that of the video.
This is how we want every math lesson to look and feel as we explore new concepts and sharpen our mathematical skills.
Post continues after this section…
DOWNLOAD THE 3-PART FRAMEWORK GUIDEBOOK

Why not bring the 3-Part Framework Guidebook with you?
Download the PDF so you can share with your professional learning network via print or email!
But that’s not how we did it in the beginning
What we’ve just described represents years of experimentation and many failures in order to understand more specifically what elements are necessary in each lesson to consistently spark curiosity in order to fuel sense making.
When we first started tinkering with the idea of curiosity and wonderment, we would save these “real world” math tasks for after we had already pre-taught the steps, procedures, and algorithms during a traditional lesson. We were killing the curiosity by providing too much information upfront.
For example, if we were teaching solving proportions, we would:
Pre-teach all of the steps/procedures and rush to an algorithm and/or trick pushing memorization before understanding. In this case, likely promoting cross multiplication or similar.
Ask students to predict what question we were fishing for by showing an image or a video like the one below:

Students would be hesitant to participate because they wouldn’t want to guess wrong.
Then, we’d share the question we were really after.
From the above video, questions might be:
- How many scoops does it take to make 3 glasses?
- How many glasses could you make with 55 scoops?
Ask students to solve the problem.
What do you think happened next?
Around half of the class would attempt solving the problem by mimicking the steps, algorithms and procedures we had shared in the examples from earlier in the lesson.
What was the other half of the class doing during this time?
You probably guessed it.
They’d be faking or stalling knowing that in just a few short minutes, we would come rescue them and “take it up” on the board.
For years we were left wondering how we could do this better. We knew that math class was way more interesting by incorporating these 3 act tasks into our lessons, but any curiosity we could muster up to interest students was always quick to fade.
Through much experimentation, reflection, and reading, we’ve done a lot of learning about what captures the attention of an audience and how we can apply this learning to make memorable experiences in math class.
From these efforts, we’ve landed on 4 big elements that go into sparking curiosity that will get your students leaning in with excitement to fuel their sense making with mathematics.
Spark Curiosity With The Curiosity Path
What was missing from our early attempts at sparking curiosity through the use of 3 act math tasks?
Well, curiosity!
By maintaining a firm hold on our traditional “I do, We do, You do” approach to pre-teach all of the rules, steps and procedures that could essentially solve the task, we were sucking out all of the curiosity.
If you want to generate curiosity rich math lessons, then we firmly believe that the best way to do it is through embedding 4 key elements we call The Curiosity Path.
The Curiosity Path
- Withhold information
- Build anticipation
- Notice & Wonder
- Estimate
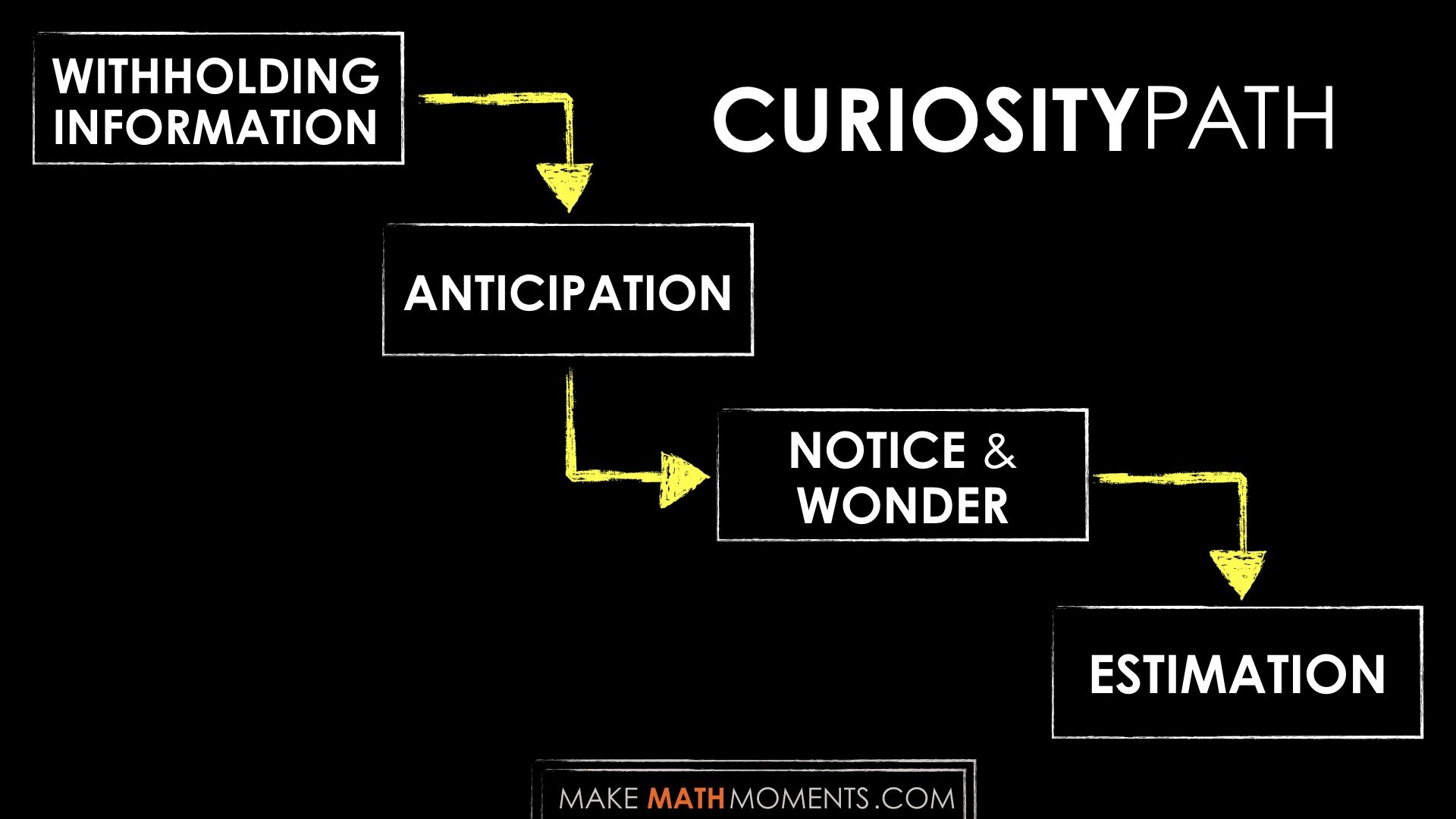

Below, we’re going to cover each part of the path and give examples so you can see them in action. Taken together, they’ll give you a framework for implementing The Curiosity Path in your own classroom.
1. Withhold Information
This first part of The Curiosity Path is all about lowering the floor to ensure all students can enter the task by avoiding the rush to steps and procedures at the beginning of the problem based lesson.
The idea is to make the entry level of the task so low that the entire class can jump in, but still interesting and thought provoking so that all students want to start participating right away.
By Withholding Information, you’re also generating moments of curiosity for every student in the room.
By offering students too much information upfront – like we typically do in a traditional lesson – any curiosity has been completely sucked out of the lesson and there’s nothing left to ponder.
But by withholding information, you can start creating that sense of wonder and curiosity so students begin asking, “what’s going on here?”
If you’re like us, then it is possible that you’ve mistakenly believed that what makes a lesson curious is by showing a video; especially a video with us (the teacher) in it!
However, those of us who have tried to incorporate a 3 act math task into a lesson have quickly realized that a video alone does not do the trick. It took us hundreds of lesson experiments to finally notice a pattern that the most curious lessons – whether created by Dan Meyer, Robert Kaplinsky, Graham Fletcher, or one of our own – are the tasks that withheld the most information.
For example, when we came across this problem in a textbook and wanted to make it more relatable:

At the time, our go-to strategies were changing the name in a problem to a student in the class, or even changing it to our name. Or, we might change the context from something “uncool” like a flowerbed or pig pen and forcing something “cool” like a cell phone:

However, those typical strategies don’t help get students to lean in and engage.
Instead of using some of these tactics, what if we stripped it down by withholding as much information as possible.
Here’s where we ended up with a problem based lesson we call Perimeter Jumble:

Rather than piling on all of the details upfront, the lack of information provides the viewer with a feeling of mystery.
You can’t help but wonder what is going on here.
Instead of overemphasizing the idea of using a “real world” or “relatable” topic to make your lesson more meaningful, remember what a great story does: it gives a little bit of information, just enough to create some compelling questions, while withholding the answers until the end.
Once you’ve withheld information and given your students something to think on, you’ve already started the second part of The Curiosity Path where we Build Anticipation.
2. Build Anticipation
The reason withholding information is such an important part of The Curiosity Path is because withholding that perfect amount of information builds anticipation in our audience.
When introducing a new concept to investigate, we could ask students to engage in a word problem, but there isn’t much that can be communicated or suggested beyond the words themselves. This can pose a problem when trying to Spark Curiosity because most word problems are just a handful of sentences and lack the detail to build up any sort of storyline or interesting context worth thinking about.
So while using videos in math class for the sake of it is no guarantee to Sparking Curiosity, you can bet that students will have a much more clear understanding of the context than if you try to boil the scenario down to 2 or 3 sentences.
If a picture is worth 1,000 words, what must a video be worth?
One researcher says at least 1.8 million words.
It might seem counterintuitive that we are encouraging thousands (or even millions) of words to be shared regarding the context of the problem we will be exploring when the first stage of the Curiosity Path is Withholding Information.
This is the beauty of approaching a problem based lesson in this way. It allows us a way to share a wealth of information about the context we will be exploring, while withholding key details that will help to build excitement, anticipation, and wonder.
For example, check out the many words that this first video from the Candle Burning 3 act task paints for students while leaving out many key details:

Doesn’t this video get you to immediately begin wondering?
Without even asking, many students are already moving on to the next phase of The Curiosity Path.
3. Notice and Wonder
So far, we’ve introduced an exercise that consciously withholds information and introduces that task in a way that gets students to start anticipating what is happening.
Despite the fact that this process helps to get at the natural curiosity we are all born with, since math class is traditionally taught without much curiosity or wonderment, we typically have to be more explicit by inviting students to allow their suppressed curious tendences to resurface.
This is why before we show a video or image in a problem based lesson we invite students to engage in a Notice and Wonder protocol by creating a T-chart with Notice and Wonder as the headings.

For example, prior to showing the first video from the R2D2 Post-It Notes task, ask students everything and anything they notice and wonder:

Your students might jot down things like:
- How long did it take to finish putting up the post-its?
- What picture are you making?
- He’s wearing shorts.
- Those are old curtains.
- How many post-its does it take to fill up the board?
- … and many more.
This might feel awkward for students initially. Remember, it is likely that they are not used to learning mathematics in this way and thus you might even feel some pushback.
In order to ensure students feel comfortable sharing what they’ve noticed or wondered, we tend to give students 60 to 90 seconds to Think-Pair-Share (or a similar protocol) because sharing with a neighbour is much less threatening and it gives them an opportunity to feel validated.
This process allows students get a chance to “test” their ideas with 1 or 2 people instead of on the whole class. This is an extremely important investment of time to ensure that students will be ready and willing to share their ideas with the whole group.
Let students share whatever they observed and be sure not to funnel student thinking by over-emphasizing your excitement when a notice or wonder related to mathematics is shared. This helps get everyone involved, actively trying to figure out what’s going on, and feel like they’ve contributed something to the lesson.
Empowering Student Voice
By asking your students what they notice and wonder, you’re empowering them to help shape the path of the lesson and to share their voice.
Make an effort to answer as many of the student wonders that you can upfront and save some of the others that will require us to do some more digging.
Even though every problem based lesson has a specific learning goal we are trying to elicit, encouraging students to Notice and Wonder makes them feel like they have some influence and power as opposed to just being directed to follow along and mimic as is often expected in a traditional lesson structure.
From there, you can pick the student’s wonder that’s closest to the one that you’ve planned to address, guiding the lesson in the direction you want it to go while also empowering that student whose wonder was selected.
And, sometimes, a specific question doesn’t come up.
No fear!
Anticipate ahead of time what some of the noticings and wonderings are that students might come up with and which you could use to still get to your learning goal.
After the lesson, circle back and address some of the other wonderings as well, further solidifying the belief that it is always worthwhile to share their thinking in math class.
Not a stand alone protocol
It can be easy to misinterpret each element in The Curiosity Path as a “standalone” protocol, but that simply is not the case.
Early on in our transformation from the traditional gradual release of responsibility model to a problem based lesson format, many of our lessons flopped and it was because we were missing parts of The Curiosity Path.
It took us a long time to learn that the success of a Notice and Wonder protocol hinges on how effectively the task creates the feeling of Anticipation through the Withholding of Information.

If we have not intentionally crafted the task to Withhold Information in order to generate Anticipation, there will be nothing there to encourage students to Notice and Wonder.
4. Estimate
After all of this hard work Withholding Information to Build Anticipation for a student voice filled Notice and Wonder experience, we are now ready to hook students in even further through one of the most important, yet underemphasized numeracy skills: Estimation.
Not only is Estimation an incredibly important mathematical skill that students need much more experience with, but it is also a great way to continue hooking students into the task.
By asking students to first think of an estimate and then share it with their neighbours, we are essentially influencing students to invest more of their time, focus, and interest in the problem all while having them utilize their spatial reasoning skills prior to jumping to steps, procedures, and algorithms.
Some teacher prompts you might keep in your bag of tricks include asking what seems unreasonable in this situation or ask them to frame out a “range of reasonableness” by sharing estimates that would be too low or too high.
For example, in the Doritos Roulette 3 Act Math Task, the stage is set for the Notice and Wonder protocol by creating Anticipation through the Withholding of Information:

After sharing out what students noticed and wondered, we land on the question:
How many hot chips are in the bag?
It is at this point where we can get kids sharing out those estimates based on their prior knowledge and experience of standard chip bags and what they can judge from the video.
As students begin sharing out their estimates – first with their neighbours and then with the whole class – what you’ll see is quite amazing.
Typically, the first few estimates are given without much emotion. But watch what happens as more and more estimates come forward. Suddenly, even the student who appears to be most disinterested in the discussion comes to life when they realize that many of the estimates being shared are completely absurd compared to the estimate they had in mind. Now they’re eager to get their voice into the mix and ensure that when the actual number of chips is revealed that everyone knows that their estimate was most precise.
Now that estimates have been made by all students in the class and many have been shared and documented for the whole class to reflect on, we can move into the real reason why we want to Spark Curiosity in the first place…
… to Fuel Sense-Making.
Post continues after this section…
DOWNLOAD THE 3-PART FRAMEWORK GUIDEBOOK

Why not bring the 3-Part Framework Guidebook with you?
Download the PDF so you can share with your professional learning network via print or email!
Part 2: Fuelling Sense-Making

As teachers, we often become so hyper-focused on creating engagement that we forget about the math.
With student engagement being such a challenge, especially as students head into the middle and high school grades, it’s easy to become so honed in on gaining the attention of our students that we lose sight of why we’re trying to engage them in the first place: to help them understand the mathematics.
While it is extremely important to find a way to engage our students and get them leaning in during our lessons, the result is empty and meaningless if we fail to help students make sense of the mathematics we are uncovering.


Let’s dive deeper into the importance of Fuelling Sense-Making.
Why it’s important to Fuel Sense-Making in students
As soon as we began to feel like we had made real progress towards Sparking Curiosity with our students and began uncovering the elements of The Curiosity Path, we started to notice a new problem of practice emerging.
Our students were more engaged than ever, but they still weren’t making sense of the mathematics.
We had been working overtime to find ways to consistently Spark Curiosity in our students, but when it came time to teach new concepts and skills, we found ourselves resorting to what we knew best: teaching steps, procedures and algorithms.
We would spend a significant amount of time planning and delivering tasks to get them curious, but then we would rob students of all thinking by showing them how to solve problems with examples before giving them the chance to persevere through any real problem solving.
What we have learned throughout this journey is that while Sparking Curiosity is important and even essential for leading an effective mathematics lesson, all efforts are wasted if used in isolation without the intent to Fuel Sense-Making.
By providing students with opportunities to Fuel Sense-Making, these engaged students can now leverage that curiosity and newfound interest to build the much needed conceptual understanding required to make connections and foster a productive disposition towards mathematics.
While there are many ways to Fuel Sense-Making in mathematics, we have four “go-to” tools that you can leverage during every math lesson to help students make connections and build conceptual understanding of new concepts while developing procedural fluency over time.
Fuel Sense-Making Tool #1: Concrete Manipulatives
Before transforming our math classrooms from a gradual release of responsibility model to incorporating the Make Math Moments 3-Part Framework, we would often use direct instruction to introduce a new concept by first modelling the steps, rules, procedures, and algorithms before spending the remaining time trying to explain why they all worked.
The problem with this approach is that we started from what was unknown to the students and tried to help them work their way back to what they did know rather than lowering the floor so they could utilize their prior knowledge and build connections to the new concept.
In order to begin math lessons where students are able to access prior knowledge, we must avoid rushing to abstraction by using meaningful contexts and starting concrete.
Take the Coffee Quantity task inside the Make Math Moments Academy. In this late elementary / middle school problem based lesson, students watch a Keurig coffee maker brewing mugs of coffee repeatedly until the “add water” light goes on.
After Sparking Curiosity with The Curiosity Path, the question we land on is:
How many mugs of coffee can be made with the remaining water in the reservoir?
Students are then given the following information:

- There were 8 cups of water in the reservoir prior to brewing;
- There were 5 mugs of coffee brewed after the add water light went on; and,
- There was 1 cup of water remaining in the reservoir.
This task is a great task for Fuelling Sense-Making with fractional thinking, however it can be extremely difficult if students attempt rushing to procedures and abstraction.
Oh, did I mention that we don’t use calculators to assist us with this (or really, any) tasks that we intend to use to Fuel Sense-Making for building conceptual understanding.
So what might starting concrete with this particular task look like?
Well, using math manipulatives such as connecting cubes can be helpful for organizing thinking.
While the reservoir had 8 cups of water to begin with, since there was 1 cup of water remaining when the “add water” light went on, we know that 7 cups of water was shared fairly amongst 5 mugs.
Here’s what this might look like:

Not only is starting concrete helpful for students to build on their prior knowledge, but it is also essential for Fuelling Sense-Making around what is happening and why things work mathematically.
While it might seem obvious that we are simply dividing 7 cups of water amongst 5 mugs, what might not be so obvious initially is that there are two types of division.
It’s O.K. if you’re thinking:
“I was today years old when I learned about the two types of division!”
We’re with you on that!
We had been teaching for over 10 years prior to realizing that division can be looked at two ways and the context drives which type is taking place.
By starting concrete with this task, students can physically distribute the 7 cups of water to the 5 mugs to reveal the rate of cups of water per mug (or the inverse rate; mugs per cup of water):
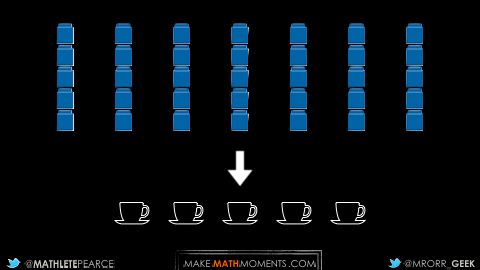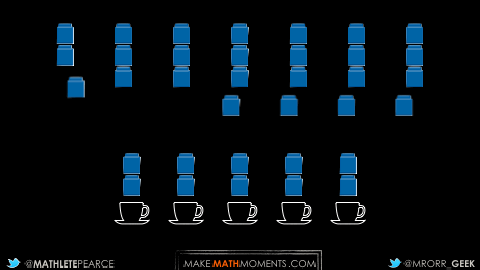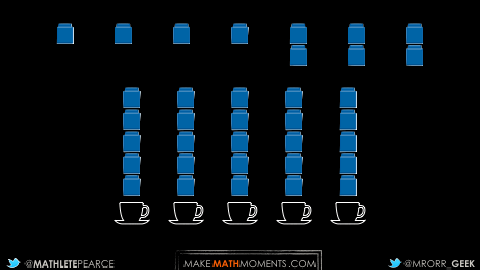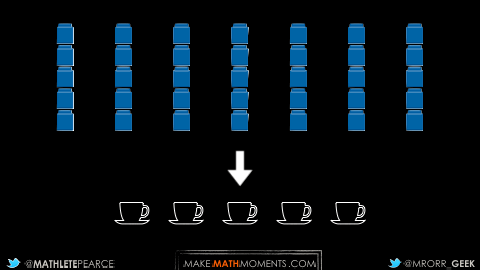
Since we partitioned each cup of water into fifths, you can see that each cube represents 1 fifth of a cup of water.
Since each mug received 7 cubes, we can say that each mug of coffee uses 7 fifths cups of water or 1 and 2 fifth cups of water per mug.
What starting concrete can also do for us is allow us to make connections and see new perspectives through the use of representations.
For example, by recalling our 7 cups of water partitioned into 5 parts, we know that each blue cube represents 1 fifth of a cup of water.
However, we can also determine how many mugs of coffee each blue cube represents by considering the inverse rate:

We can see that the rate or constant of proportionality can be considered in two ways:
7 fifth cups of water per mug of coffee
Or, inversely:
5 sevenths mugs of coffee per cup of water
What is easy to miss here is how important authentically engaging in the problem solving process and physically manipulating the connecting cubes is for Fuelling Sense-Making. When you (or students) are simply being told through a series of images like we are here in this article, we (the authors of this post) own the thinking here instead of you (or your students).
Be sure to allow for the time necessary for students to authentically engage in tasks so they are given the time and space to make sense of the mathematics. Through doing so, new strategies and mathematical models will begin to emerge.
This is where we come in to nudge their thinking forward.
This idea of starting concrete has many different names such as:
- Concreteness Fading;
- Concrete, Representational, Abstract (CRA);
- Concrete, Pictorial, Abstract (CPA); and,
- Experiential, Language, Pictorial, Symbolic (ELPS).
While the big idea remains the same, unfortunately many of the resources that highlight these ideas for starting concrete can promote (sometimes unintentionally) the rush to proceduralizing these concepts rather than building the necessary understanding first. So read the CRA, CPA, and ELPS links above with this in mind.
Two ways to use concrete manipulatives for thinking
Concrete manipulatives can be used in two ways during an effective mathematics lesson; as a tool for thinking and as a tool for representing thinking.
When first introducing a new mathematical concept, it can be helpful for students to use concrete manipulatives as a tool for thinking to help them solve problems and arrive at a solution. This is especially true for students who are not yet able to visualize a mathematical idea in their mind and must physically manipulate manipulatives representing quantities to develop an understanding and trust of the mathematical behaviours and patterns they are observing.
When educators hear the word “manipulatives” in math class, many get the image of a struggling student who is dependent on these concrete tools to solve a problem using inefficient strategies. However, this is a narrow view of both how manipulatives can be used as a tool for thinking in the math classroom as well as pigeonholing strategies used with manipulatives as being inefficient.
Manipulatives can and should be used as a tool for thinking as well as a tool to represent thinking so that students can build all 5 mathematical proficiencies. However, if the focus in the math classroom is to memorize steps and procedures over understanding, then it is difficult to shift beliefs away from manipulatives being tools only for those who struggle.
So, how can we change this misconception?
By valuing students demonstrating understanding over mindless memorization.
One of the best ways for students to clearly demonstrate their conceptual understanding of how mathematics works is by using concrete manipulatives as a tool to represent thinking.


A student who has a deep conceptual understanding of mathematics may not yet have developed the adaptive reasoning skills necessary to explain their thinking to another classmate or the teacher. When a student represents mathematical thinking using symbols and algorithms, a great question to ask students is to convince you of why what they’ve written actually works. It is when students are asked to convince their mathematical community of their thinking that concrete manipulatives can be called upon for use as a tool for representing thinking. Many students will balk at the idea initially, however with persistence, students will realize that the process of reasoning and proving is the doing of mathematics rather than mindless memorization.
By focusing on the building of conceptual understanding in math class, students will be able to move from concrete to abstract thinking over time, while also becoming procedurally fluent with various algorithms and procedures that they learn to remember and trust.
Fuel Sense-Making Tool #2: Multiple Representations
The second go-to strategy to Fueling Sense-Making in math class involves helping students to make connections across multiple representations. As we learned in the previous strategy, using concrete manipulatives is not only a helpful tool for thinking, but also to represent thinking.
When we think about mathematics, it is representations that allow us to access and build understanding of each concept. Whether you learned in a classroom that focused primarily on abstract representations using symbolic notation like numbers, letters, and symbols, or in a classroom that used a variety of concrete, verbal, visual, and abstract representations, every mathematical concept must accessed through representation.
The challenge we face as mathematics educators is being flexible enough in our own thinking to see and connect multiple representations of mathematical concepts while helping students develop their own understanding through their eyes.
Because students are engaging in mathematics through a problem based learning model, this means we cannot simply show students multiple representations, but rather elicit student thinking to emerge new mathematical models and make connections across representations during the consolidation of the lesson.
Back when we taught our lessons through telling, we would plan each of the strategies that we would show students in the lesson and then essentially tell students which strategy to use.
For example, when teaching linear relations, we would start with tables, then move to graphs, and finally equations.
We now realize that by delivering problem based lessons and teaching through task, we can better meet students where they are in their learning journey by leveraging their strategies and representations of the mathematics and building off of that.
It is common when we try to make a shift from the “Rush to the Algorithm” to teaching through conceptual understanding in order to build procedural fluency to apply our old habits to strategies and mathematical models. Now that we realize the importance of multiple representations, we rush to showing students strategies and showing all of the mathematical models that can be used as tools for thinking and to represent thinking.
While this might be more helpful than rushing to symbolic algorithms alone, it promotes the proceduralization of these representations rather than the conceptual understanding that we are seeking.
Instead, we want to elicit student thinking and assist in the development and emergence of strategies and mathematical models.
Here’s the result of leading a math talk involving a string of related problems inspired by Minilessons by Cathy Fosnot.
The string was:
12 candies ÷ 4 candies per bag
24 candies ÷ 4 candies per bag
24 candies ÷ 8 candies per bag
[Want a set of those Wipebook Flipcarts? Get 40% off here.]
Through a math talk routine, I annotated student thinking and did my best to help models emerge based on the strategies students were sharing. This process allows students to see their thinking through multiple representations and begin the journey from seeing their thinking represented in another mathematical model to being able to use that model as a tool for thinking and to represent their thinking.
On the other hand, if we pre-teach students a strategy – often times, what we (the teacher) perceive as the most efficient strategy – and ask students to use that same strategy and mathematical model to solve similar problems, we risk killing the curiosity we worked so hard to create earlier in the lesson and likely promoting the disengagement of any student who is unable to see their own thinking in this single method being shared.
It is the imposing of a strategy and mathematical model by the teacher that perpetuates our perception that students are unable or unwilling to think.
This is our doing and thus, we must undo this.
Promoting students to apply and share their own strategies in our math classrooms is a great way to slowly bring student thinking into the math classroom.
Fuel Sense-Making Tool #3: Visuals
So, we’ve convinced you that bringing multiple representations into your classroom through student thinking is necessary for building conceptual understanding through reasoning and proving.
Amazing!
Now we need to broaden our understanding of how we represent mathematics beyond the concrete (tool #1) and abstract (what most of us are comfortable with).
There is this place right in the middle that is a perfect bridge between modelling mathematics concretely with real world objects or manipulatives and abstractly with symbols and notation where we begin drawing representations of what we know and see concretely.
This stage leverages drawings or pictorial representations that provide a visual for the learner to both see on the page and help begin making a mental image in their mind’s eye.
For example, when learning about early subtraction, we might give students a problem like:
There are 12 cookies.
Your friends eat some and there are now 8 left.
How many cookies were eaten?
I think we can all agree that if this was the beginning of this idea, we might want to spruce this up by Sparking Curiosity through The Curiosity Path like we do in the Gummy Worms task, however let’s focus on how we can use visuals right in the middle of concrete and abstract representations to Fuel Sense-Making.
First, students should have the opportunity to start concrete by either using actual cookies or possibly connecting cubes, counters, or other manipulatives to represent this scenario and their thinking.
We as the facilitator of this learning experience can then begin eliciting student thinking in concrete form and representing their thinking visually.
This might mean drawing something like a part-part whole model to nudge students towards organization:

If students were using real cookies or plastic cookies as a tool for thinking, then we might try modelling their thinking using connecting cubes to begin to emerge what appears to be a concrete number line as we nudge forward in the abstraction journey:

We would draw some of these concrete representations on a chalk/whiteboard or chart paper to help students begin to see that drawings can be helpful to represent real, concrete situations.
As students become more comfortable with this thinking, we can begin to emerge the concrete number line further and eventually, head to a more abstract, but still very visual number line:

As students make connections amongst these different representations over time, we can then begin to emerge symbolic models involving numbers and symbols.
Essentially, this subtraction problem involves a missing subtrahend that can be modelled algebraically as:
12 – ___ = 8
Or, when appropriate:
12 – x = 8
Students are not only developing their understanding of subtraction here, but they are also building algebraic reasoning.
It is completely natural if you are feeling a bit worried or even overwhelmed by the thought of learning about multiple representations for all of the curriculum content you must teach. Most of us did not have the benefit of learning through conceptual understanding and thus we have a lot of learning to do ourselves in order to effectively deliver mathematics lessons that truly Fuel Sense-Making rather than rush to algorithms and memorization.
Luckily, we try to share as much as possible in a visual fashion so that we can all get better at conceptualizing the mathematics we have to teach and develop our repertoire of mathematical models and representations. One place you might start your visualizing mathematics journey is at our website, MathIsVisual.com where we share a ton of mathematics concepts visually.
Fuel Sense-Making Tool #4: Student-Generated Solutions
Student-generated solutions, or student-generated algorithms, is our fourth tool for Fueling Sense-Making – and it’s a big one.
We touched on this earlier, but it is worth mentioning again that once we’ve sparked that curiosity with our students, we must resist the temptation to rob them of their thinking by just showing them how to solve the problem. Instead, pose purposeful questions to craft opportunities for productive struggle.


Giving students the necessary time and space to investigate and reason through problems using their own tools and strategies to arrive at a solution is useful for many reasons, however there are three extremely important benefits that we missed out on when we taught using the I do, We do, You do model.
The first benefit involves maximizing the curiosity we worked so hard to create earlier in the lesson. If we pre-teach students the most efficient tool and strategy to use to solve a problem upfront, not only do we immediately exclude some learners who are not ready for that approach, but we completely kill any curiosity that we had developed to that point.
The second benefit is the development of grit and resilience to persevere through challenging problems. By promoting students accessing the tools and strategies they have build a comfort with, we provide them with an opportunity to productively struggle through problems and build confidence as well as a productive disposition towards mathematics.
Finally, by observing the tools and strategies students are using and asking students to share their thinking, we gain a wealth of assessment information each and every day that we can use to guide our instruction. From which solution strategies we can use during the consolidation to make connections amongst multiple representations, to which concepts we need to spiral back to in order to dive deeper, student-generated solutions are a hidden gem that has been absent for too long in the traditional math classroom.
This concept is often foreign and very scary if you’re coming from a traditional teaching approach like we did.
I think the idea can best be summarized by Cathy Fosnot from Episode #24 of our podcast when she says that we “don’t want to fix the mathematician” but rather help the mathematician see their strategy through to the end, while nudging them to nudge their strategies forward to a higher level of sophistication.
While we’re not proud to say it, we were trying to “fix” the mathematicians in our classroom for years. If a student was using a strategy other than the “efficient” strategy that we wanted to teach that day, we would attempt to “course-correct” them to use our strategy thinking that we were helping.
The problem is, that student wasn’t approaching the problem with the same thinking as we were. It is so easy for us to forget that we have so much more experience and likely can think of the mathematical concept we are sharing much more abstractly than the learners who sit before us. This “curse of knowledge” causes us to believe that everyone in the room sees things the way we do. However, it is unlikely that students are ready to see the mathematics as clearly as we do.
Instead of trying to redirect that student away from their own thinking to get them to use a more effective strategy (and losing and/or disengaging them), consider how we might leverage their thinking and nudge them to up the sophistication of their strategy while deepening their understanding at the same time.
It is the process of eliciting student thinking and solution strategies to make connections across multiple representations that will not only keep your students engaged and invested in your math class, but it is the fuel necessary to make sense of the mathematics.
So now that we’ve unpacked how to Spark Curiosity using The Curiosity Path and 4 Go-To Tools to Fuel Sense-Making in every lesson, you’re probably wondering:
How do we make Sparking Curiosity and Fuelling Sense-Making a routine in our math class?
This is where the 3rd and most important part of the framework comes in.
DOWNLOAD THE 3-PART FRAMEWORK GUIDEBOOK

Why not bring the 3-Part Framework Guidebook with you?
Download the PDF so you can share with your professional learning network via print or email!
Part 3: Igniting Teacher Moves

The final part of the Make Math Moments 3-Part Framework is called Igniting Teacher Moves because it focuses in on the extremely important work that all educators must do to plan our math lessons with intentionality. It is this planning stage of the framework where we do all of the heavy lifting to ensure our lessons are meeting all students where they are along their math learning journey.
Because this may not be the most exciting part of the framework on the surface, it is this part of the framework that we must be considering first in order to plan effective mathematics lessons with any sort of consistency.
As Tom Shimmer stated in his book, Grading From The Inside Out:
“Plan With Precision So You Can Proceed With Great Flexibility”
~ Tom Schimmer


It is with this quote in mind that we developed the Igniting Teacher Moves portion of the 3-Part Framework to help us plan lessons that will become Math Moments in our students memories that actually matter.
The 3 Moves That Ignite Teacher Action
When we started to think deeply about what is involved in planning an effective math lesson, we began to realize that while the bulk of the planning process typically happens before delivering a lesson, we must also prepare ourselves for some of the during moves that we should be using while the lesson is taking place, and finally considering the after moves we must use when a lesson ends and we begin planning for the next.
So while we’ve categorized the important decisions that must be made to Ignite Teacher Action as before, during, and after moves, you’ll quickly realize that within each we will find a series of “sub-moves” for us to consider.
Let’s dive in.
Igniting Your Before Moves
When math educators think about planning an effective math lesson, the vision we have in our head is all of the hard work that is spent before a math lesson takes place to ensure it runs without a hitch.
For example, there is a lot of thinking that must be done to ensure that all four (4) elements of The Curiosity Path are in place so we can gain the attention of our students and get them to lean in.
We also must spend a significant amount of time before our lesson to ensure that we are leveraging tools that will Fuel Sense-Making in our students.
While there is a significant amount of time that must be spent planning to Spark Curiosity and Fuel Sense-Making, there is still some very important work still to be done.
In order for our efforts Sparking Curiosity and Fuelling Sense-Making to yield Memorable Math Moments for our students, we must be very intentional about the math concept(s) we are planning to elicit in a lesson and ensure that all students can access the content through our problem based lessons.
In order to unpack how we can Ignite Our Before Moves, we’ll break them down into three (3) parts.
Before Move #1: Know Where Your Students Are Coming From
When planning our lessons with intentionality and precision, we must consider where students are coming from.
This is a fairly broad move because you’re probably realizing that we can think about this in many different ways. Are we referring to their family history/homelife? Their ethnic background? Hobbies and interests? What peer groups they associate with? Or are we talking about what mathematical experiences and understandings they bring with them?
Although it might feel overwhelming, knowing where your students are coming from involves all of these ideas and more.
We need to know our students in order to have any remote chance at meeting them where they are in their learning journey.
As we learn more and more about each student in our classroom, we can then plan our lessons with those particular students in mind rather than teaching to the middle.
While we can’t downplay the importance of understanding who our students are as people, we also must consider where they are coming from mathematically.
Having spent all of our time teaching in high school math classes, it was just recently when we began to realize the importance of knowing where our students were coming from in their mathematical journey.
For example, spending a significant amount of time teaching grade 9 – the first year of high school here in Ontario – we made massive assumptions about what students should and would know coming into our classrooms.
We of course knew the curriculum we had to teach for our course, but we had little to no understanding of what students had been exposed to and to what depth over their previous Kindergarten through grade 8 mathematical experience.
We made assumptions that students were operating with fractions, collecting like-terms, or using the algebraic representation of Pythagorean’s Theorem for years prior to joining us in high school. After years of scratching our heads wondering why students weren’t “getting it” when we would show steps, procedures, and algorithms without developing understanding, we realized that we should probably have a look back to see what they were learning and when.
As we went back through the elementary math curriculum, we started to realize that many concepts came up much later than we assumed. Worse yet, when we began thinking about how we might help close gaps in student understanding, we quickly realized that we ourselves didn’t have the necessary conceptual understanding to help students make connections.
It was at this time when we started to realize that the student struggles we were encountering as math educators was much bigger than students not knowing their math facts like we had been saying for years.
So, slowly but surely, we began thinking through our curriculum and following concepts back to their beginnings.
Concepts like multiplying binomials in grade 10 took us on a journey all the way back to grade 5 where students begin multiplying two-digit by two-digit numbers using arrays with base 10 blocks, area models, and finally, algorithms.
How is it possible that we – two high school math teachers with degrees in mathematics – didn’t realize that multiplying binomials is conceptually the same as multiplying two digit by two digit numbers?
An unexpected benefit of reaching back to better understand where our students were coming from was the realization that all of the work in mathematics education we are doing from Kindergarten through Grade 12 is in service of helping every student along their journey and we are all doing the work together.
While it is impossible to do all of this work over a weekend, keeping this before move in mind as you move forward will help you to continually refine your own conceptual understanding of mathematics and help you to reach more students.
Before Move #2: Know Where Your Students Are Going
We know that first before move was a big one and rightfully so.
However, we’re here to let you know that it’s not enough to know where students are coming from. We also need to know where they are going.
Of course, we don’t need Grade 1 teachers to understand what students are going to be doing in Grade 10, however we do need teachers thinking about the next couple of years in a students mathematical journey.
Why is this important?
Without having an understanding of where students are heading, how will I know the depth to which I should be diving into a concept through investigations and problem solving? Often times, our current curriculum or standards documents will give us detail around what topics to uncover, however some topics may be foundational for the next grade level while others may not reappear again.
It is the time we spend during this before move that will help us determine with a higher level of precision how essential a concept is for future success and how much time we should dedicate to it.
Knowing where our students are going is also extremely important for us to gain an understanding of which mathematical strategies and models we will intentionally plan to emerge throughout our lessons from student thinking.
Again, knowing where students are going is not something we can learn overnight. However, constantly reflecting on where students are heading in the next lesson, next unit of study, and next grade level will continue to build your mathematical content knowledge and pedagogical practice that will continuously serve you and your students each and every day.
Before Move #3: Anticipating
The third before move is the anticipating we must do for our next problem based lesson.
By knowing where our students are coming from both as individuals and mathematicians, we can craft our next lesson around a task that will provide a low enough floor for all students to access while providing a high enough ceiling to ensure all students stay engaged in a productive struggle.
This particular before move as well as the four during moves are built off of Margaret (Peg) Smith and Mary Stein’s work around the Five Practices For Orchestrating Productive Mathematical Discussions.
We begin this work by planning our learning intention for the lesson by selecting which mathematical concept(s) we intend to elicit. From here, we search and refine or create a math task that will help us to emerge the mathematical strategies and models we have set out to bring forth during the lesson.
Once the task is selected, we can begin anticipating what strategies and models students might use to solve the task by attempting the task ourselves. We find it helpful to try approaching the task from the perspective of different students in your class from a range of understandings.
The process of approaching the task with various strategies and perspectives can be extremely difficult to do alone. Find colleagues at your school or online that you can buddy up with to do the mathematics together. You’ll be surprised at the different strategies and models you will encounter when doing this process with others.
With the variety of anticipated strategies and models you have come up with, begin writing down some purposeful questions that you can pose to students that will help focus their thinking rather than making statements that rob students of thinking.
By anticipating possible solution strategies and models you might encounter when delivering this problem based lesson and planning purposeful questions for each, you’ll be in a much better position to respond to student thinking in the moment rather than improvising “on the fly”.


Igniting Your During Moves
One of the biggest and unexpected shifts that we had to make moving away from teaching with a traditional gradual release of responsibility model to a Make Math Moments 3-Part Framework lesson was what to do while students are productively struggling through a math task.
We were so familiar with the routine of ending our math “lecture-style” lesson by assigning a bunch of questions for students to work on and then – like clockwork – watching a sea of hands rising to the sky in demand of our help. We would then proceed to make our way, frazzled, to as many student desks as we possibly could to “rescue” them from their unproductive struggle.
This is not what we want to be doing during a Make Math Moments Problem Based Math Lesson.
Instead, we want to be implementing four (4) during moves that we’ll be using in the moment throughout the problem based lesson to promote productive struggle and resiliency.
During Move #1: Monitoring
Once students get going on a Make Math Moments Task, we are walking the room monitoring what students are doing.
When students are just getting started on the task, it might be helpful to almost pretend you aren’t observing or listening to what students are doing to avoid them asking you proximity questions like “am I on the right track” or “I’m not sure how to get started”.
Another reason we tend to avoid appearing as though we are observing too closely when students are just getting started is to lower the stakes for students to openly brainstorm their ideas. Too often students are hesitant to share their initial thoughts and ideas openly when the teacher is lurking close by.
However, as you see groups beginning to gain traction, do get closer to listen in and pose purposeful questions to help you get a better understanding of a strategy that might be emerging as well as to help students refine, clarify, and better articulate their thinking with the group.
It is while we engage in this during move of monitoring that we begin executing the next move.
During Move #2: Selecting
As we continue to monitor students engaging in the problem solving process, we begin to see some of the solution strategies and models that we had anticipated as well as some others that we may not have considered.
While we continue to pose purposeful questions to help each group see their strategy through, we are also paying special attention to which groups are using what tools, strategies and mathematical models for us to consider selecting during the consolidation of the task.
Although we had committed a significant amount of time to anticipating what we might see before delivering this lesson, we are now forced to make some decisions in the moment regarding which student work samples we will select to include in the body of work for consolidation. Regardless of how much time and effort we spend anticipating, we will still be required to think on our feet and be responsive based on the student work being generated in the moment. So even though we may have what we believe to be a bulletproof plan for how we’ll consolidate the task, it will not be helpful if the connections we want to make are based on the teacher’s thinking rather than the thinking of students in the room.
During Move #3: Sequencing
As we are selecting student work, we are also thinking about the order in which we should highlight that work during consolidation. Again, we should have an idea of how we want to select and sequence student work based on the before move of anticipating that we had planned prior to delivering this lesson, but that of that preparation is done to give us the flexibility to pivot in the moment based on the student thinking that we’re seeing and hearing around the room.
There are many ways that you can consider sequencing student work for consolidation. Here are a few for consideration:
- Most accessible (i.e.: often more concrete) to least accessible solution strategy (i.e.: often most abstract/symbolic);
- Most common/frequent to least common tools, strategies, and mathematical models; or,
- Choose another approach to select and sequence student work.
Although our most used strategy for sequencing student work tends to be from most accessible solution strategy to least accessible, the approach you use for each lesson should depend on the learning goal you are hoping to elicit and based on what you’re seeing in your classroom.
During Move #4: Connecting
The last of the Igniting Teacher “During” Moves is also the last of the Five Practices and is really the reason we need to monitor, select, and sequence in the first place: for connecting solution strategies and mathematical models for building a deep conceptual understanding.
It is at this point when we as the facilitator of the mathematics learning in our classroom take all of the information we’ve gleaned from the before and during moves to put the pieces together in such a way that will help students take the sense they’ve made of the mathematics thus far and make connections to solidify their understanding.
We view this portion of the lesson as a miniature version of knowing where students are coming from and helping students to see that regardless of which solution strategies and models they may have used to solve this math problem, there are other strategies they could have used and they can see their thinking in other student strategies and models.
By challenging students to solve problems using the tools, strategies and models they have in their tool belt, pushing their thinking forward via purposeful questioning, and asking them to look for their thinking in the thinking of others, we are setting the grounds for students to see mathematics from multiple perspectives, reason through problems, and build mathematical flexibility.
It is also important to note that the during moves of monitoring, selecting, and sequencing is all in service of making connections to the new learning objective for the lesson. That means that we are not sharing every piece of student work nor should we pass the mic off to students to do a complete “show and tell” of their entire approach and strategy. We as the facilitators must think of the specific reason why we selected that piece of student work and we can either ask those students to share specific parts from their work or, even better, ask other students in the room to attempt explaining what they think that group might be trying to communicate. Regardless of how you choose to deliver this portion of the lesson, be aware that while time is a valuable resource, what might be even more limited is the attention of our students. The longer the consolidation goes on, the less likely it is that students will have made the connections you were hoping for.


Next Move: Proceed or Pivot?
All teachers – regardless of subject area – are big on long range planning.
We’ve been told since our pre-service schooling that we should follow a pacing guide or make your own long range plan that will map out exactly what you’re going to teach, the order you’re going to teach it in, and when exactly you’ll be teaching it.
While we’re certainly not suggesting that you don’t make a long range plan, what we are saying is that we must give ourselves the permission to proceed or pivot from that plan based on the learners in our room.
For years, we would make a long range plan and we would stick to it. We were experts at “covering curriculum”, but with just one problem… only some students were understanding what we were covering.
We were planning our entire math course before we had even met our students. We had no idea where they were coming from nor what assets they were bringing with them. This approach to planning kept only that 1 student “in the middle” in mind, despite the fact that we knew that we would be teaching a diverse group of 30 students.
This “teaching to the middle” approach forced us to try dragging students who were not ready to access the mathematical content along by promoting the memorization of steps, rules, and procedures without understanding while also holding up students who were well beyond the math content we had planned our lesson for. Not only did this cause us much stress and anxiety for the better part of our career, but students outside of the middle weren’t benefitting.
With the Make Math Moments 3-Part Framework, we are now reflective after each math class – just as we want our students to be – in order to decide whether we should proceed as planned or whether we need to pivot our plan.
By using your long-range plan as a guide, but not the rule, you will give yourself the freedom to meet students where they are and help nudge them further along their mathematical journey.


Ready To Take A Deep Dive?
Wow!
You made it through the massive journey unpacking our Make Math Moments 3-Part Framework.
Bravo!
Clearly, you’re eager to transform your lessons from the “I do, We do, You do” approach to a problem based approach that students will not only love, but also learn from.
While many of the tools necessary to begin your math lesson transformation are all included in this Guidebook, it takes a lot of time, effort, and experience to build consistency Making Math Moments That Matter for your students each day.
If you’re interested in diving deeper, be sure to register for our 12-week, self-paced, online workshop that will guide you from start to finish and expedite the process.
REFERENCES:
“Asking Questions and Promoting Discourse.” National Council of Teachers of Mathematics, www.nctm.org/Conferences-and-Professional-Development/Tips-for-Teachers/Asking-Questions-and-Promoting-Discourse/.
Bruce, C. (2014a). “Spatializing” the mathematics curriculum: New perspectives, new frameworks. Proceedings of the 38th Conference of the International Group for the Psychology of Mathematics Education. Vancouver, BC: PME.
Clements, D., & Sarama, J. (2009). Learning and teaching early math: The learning trajectories approach. New York, NY: Routledge.
Dreher, Anika & Kuntze, Sebastian & Lerman, Stephen. (2015). Why Use Multiple Representations in the Mathematics Classroom? Views of English and German Preservice Teachers. Int J of Sci and Math Educ. 1-20. 10.1007/s10763-015-9633-6.
Durksen, Tracy & Way, Jennifer & Bobis, Janette & Anderson, Judy & Skilling, Karen & Martin, Andrew. (2017). Motivation and engagement in mathematics: a qualitative framework for teacher-student interactions. Mathematics Education Research Journal. 29. 10.1007/s13394-017-0199-1.
Evertson, Carolyn M., et al. “Relationships between Classroom Behaviors and Student Outcomes in Junior High Mathematics and English Classes.” American Educational Research Journal, vol. 17, no. 1, 1980, pp. 43–60. JSTOR, www.jstor.org/stable/1162507. Accessed 28 Jan. 2020.
Fosnot, Catherine Twomey, and Willem Uittenbogaard. Minilessons for Extending Multiplication and Division: A Yearlong Resource. Pearson Education, 2008.
Hetika, Hetika & Farida, Ida & Priatnasari, Yeni. (2018). Think Pair Share (TPS) as Method to Improve Student’s Learning Motivation and Learning Achievement. Dinamika Pendidikan. 12. 125-135. 10.15294/dp.v12i2.13561.
Killian, Shaun. “8 Ways to Use the I Do WE Do YOU Do Model to Boost Student Results.” Evidence, 22 Nov. 2019, www.evidencebasedteaching.org.au/the-i-do-we-do-you-do-model-explained/.
King, A. (1994). Guiding Knowledge Construction in the Classroom: Effects of Teaching Children How to Question and How to Explain. American Educational Research Journal, 31(2), 338–368. https://doi.org/10.3102/00028312031002338
Lawrence Weinstein and Adams, John. Guesstimation. (Princeton University Press. 2008).
Leutzinger, L. P., Rathmell, E.C., & Urbatsch, T.D. “Developing estimation skills in the primary grades.” In Estimation and Mental Computation: (1986 Yearbook, edited by H. L. Schoen and M. J. Zweng, 1986, 82-92. Reston, VA) National Council of Teachers of Mathematics.
Liljedahl, Peter. “Building a Thinking Classroom in Math.” Edutopia, George Lucas Educational Foundation, 17 Oct. 2017, www.edutopia.org/article/building-thinking-classroom-math.
Liljedahl, Peter and Darien Allan. “STUDENTING: THE CASE OF “NOW YOU TRY ONE”.” 2013, http://www.peterliljedahl.com/wp-content/uploads/PME-2013-Studenting-2.pdf
McQuivey, James. (2008). How Video Will Take Over The World: What The Rise Of OmniVideo Means For Consumer Product Strategy Professionals.
https://www.forrester.com/report/How+Video+Will+Take+Over+The+World/-/E-RES44199
Meyer, Dan. “The Three Acts Of A Mathematical Story.” Dy/Dan, 6 Aug. 2016, blog.mrmeyer.com/2011/the-three-acts-of-a-mathematical-story/.
Mulvahill, Elizabeth. “10 Fun Alternatives to Think-Pair-Share.” WeAreTeachers, 29 Aug. 2019, www.weareteachers.com/think-pair-share-alternatives/.
National Research Council. 2001. Adding It Up: Helping Children Learn Mathematics. Washington, DC: The National Academies Press. https://doi.org/10.17226/9822.
Newcombe, N. S. (2010). Picture this: Increasing math and science learning by improving spatial thinking. American Educator, 34, 29–35.
Orr, Jon & Pearce, Kyle. “Episode #21: The Thinking Classroom: An Interview with Peter Liljedahl.” Make Math Moments, 22 Apr. 2019, makemathmoments.com/episode21.
Orr, Jon & Pearce, Kyle. “Episode #24: Landscapes of Learning : An Interview With Cathy Fosnot.” Make Math Moments, 13 May. 2019, makemathmoments.com/episode24.
Orr, Jon & Pearce, Kyle. “Episode #24: The 5 Practices: An Interview with Peg Smith.” Make Math Moments, 15 Jul. 2019, makemathmoments.com/episode33.
Orr, Jon. “Building Resilient & Determined Math Students.” Mr. Orr Is A Geek, 25 Feb. 2018, mrorr-isageek.com/building-resilient-determined-math-students.
Orr, Jon. “Perimeter Jumble” Mr. Orr Is A Geek, 20 Dec. 2016, tapintoteenminds.com/3act-math/candles-burning.
Orr, Jon. “Spiralling Grade 9 Applied Math” Mr. Orr Is A Geek, 04 Feb. 2015, mrorr-isageek.com/spiralling-grade-9-applied-math/.
Pearce, Kyle. “Candle Burning” Tap Into Teen Minds, 14 Oct. 2013, tapintoteenminds.com/3act-math/candles-burning.
Pearce, Kyle. “Does Memorizing Multiplications Hurt More Than Help?” Tap Into Teen Minds, 20 May. 2016, tapintoteenminds.com/memorizing-multiplication-tables-hurt-help.
Pearce, Kyle. “Doritos Roulette: Hot Or Not?” Tap Into Teen Minds, 31 Mar. 2015, tapintoteenminds.com/3act-math/doritos-roulette-hot-or-not.
Pearce, Kyle. “Gummy Worms” Tap Into Teen Minds, 01 Jan. 2018, tapintoteenminds.com/3act-math/gummy-worms.
Pearce, Kyle. “The Complete Guide To Spiralling Your Math Curriculum” Tap Into Teen Minds, 20 May. 2016, tapintoteenminds.com/spiralling-guide.
Pearce, Kyle. “Using Tasks To Teach Lessons” Tap Into Teen Minds, 26 Dec. 2017, tapintoteenminds.com/tasks-teach-lessons.
Pearce, Kyle. “Why I Ask Students To Notice and Wonder” Tap Into Teen Minds, 13 Nov. 2017, tapintoteenminds.com/notice-wonder.
Pressfield, Steven. “Three Act Structure.” Steven Pressfield, 15 Apr. 2011, stevenpressfield.com/2011/04/three-act-structure/.
Putri, Hafiziani & Misnarti, Misnarti & Saptini, Ria. (2018). INFLUENCE OF CONCRETE-PICTORIAL-ABSTRACT (CPA) APPROACH TOWARDS THE ENHANCEMENT OF MATHEMATICAL CONNECTION ABILITY OF ELEMENTARY SCHOOL STUDENTS. 10. 61. 10.17509/eh.v10i2.10915.
Reys, Robert E., Marilyn N. Suydam, Mary M. Lindquist, and Nancy L. Smith. Helping children learn mathematics (Fifth edition). (Needham Heights, MA: Allyn & Bacon 1998).
Sampsel, Ariana, “Finding the Effects of Think-Pair-Share on Student Confidence and Participation” (2013). Honors Projects. 28. https://scholarworks.bgsu.edu/honorsprojects/28
Schimmer, T. (2016). Grading from the inside out: Bringing accuracy to student assessment through a standards-based mindset. Bloomington, IN: Solution Tree Press.
Skilling, Karen. (2014). Teacher Practices: How they Promote or Hinder Student Engagement in Mathematics.
Smith, Margaret S, and Mary K. Stein. 5 Practices for Orchestrating Productive Mathematics Discussions. Reston, VA: National Council of Teachers of Mathematics, 2011. Print.
Taylor-Cox, J. 2001. “How many marbles in the jar? Estimation in the early grades.” Teaching Children Mathematics, 8, 208-214.
Wheeler, Laura. “Delving into @Pgliljedahl’s #ThinkingClassroom.” Twitter, 25 Feb. 2017, twitter.com/wheeler_laura/status/835590169109606402.

WHY NOT TAKE THE GUIDEBOOK WITH YOU?

DOWNLOAD THE 3-PART FRAMEWORK GUIDEBOOK

Why not bring the 3-Part Framework Guidebook with you?
Download the PDF so you can share with your professional learning network via print or email!
Why not join our year-round membership platform packed with courses, problem based tasks, past Virtual Summit Session Replays, and a vibrant community forum to jump-start your journey to Make Math Moments during each and every lesson.
Try it FREE for 30 days!
11 Comments
Trackbacks/Pingbacks
- Episode #69: How Can I Get More From My Students? A Math Mentoring Moment - Make Math Moments - […] https://makemathmoments.com/framework […]
- How To Make Math Moments From A Distance | Teaching Remotely - […] the Spring of 2020, we hosted a series of webinars to help share how we can apply the Make…
- Lecture Learning vs. Active Learning | Is the debate dead? - […] You can learn about the 3-Part Framework by reading our Complete Guide here. […]
- How To Use Google Slides For Math Portfolios - […] The Make Math Moments 3-Part Framework Guidebook […]
- Page not found - Make Math Moments - […] The Make Math Moments 3-Part Framework Guidebook […]
- How to Build Number Sense and Fluency In Your Math Class - […] The Make Math Moments 3-Part Framework Guidebook […]
- Episode #154: Making Changes While Staying Aligned - A Math Mentoring Moment Episode - […] The Make Math Moments 3-Part Framework Guidebook […]
- How to Emerge Mathematical Behaviours Through Questioning - […] The Make Math Moments 3-Part Framework Guidebook […]
- Episode 157: How To Flip Your Math Class The Right Way! - […] The Make Math Moments 3-Part Framework Guidebook […]
- Episode #158: Don’t Ditch Your Lesson Model; Reverse It! - A Math Mentoring Moment Episode - […] The Make Math Moments 3-Part Framework Guidebook […]
- Episode #159: Why Your Math Lesson Keeps Coming Up Short - […] The Make Math Moments 3-Part Framework Guidebook […]
- How To Make Better Choices In Math Class - […] The Make Math Moments 3-Part Framework Guidebook […]
- How To Avoid The Rush to the Algorithm With THIS Common Concept - […] The Make Math Moments 3-Part Framework Guidebook […]
- 4 Ways To Find Awesome Math Resources | Our Go To Math Lesson - […] The Make Math Moments 3-Part Framework Guidebook […]
- Teach Algebra: Substitution & Solving Equations | Classroom Sneak Peek - […] The Make Math Moments 3-Part Framework Guidebook […]
- How To Solve Proportions Without Cross Multiplication | Ratios, Rates and Proportionality - […] The Make Math Moments 3-Part Framework Guidebook […]
- Free Random Grouping Cards For Visible Random Groupings - […] The Make Math Moments 3-Part Framework Guidebook […]
- Episode 172: Avoid These Misconceptions to Teach Problem-Based Lessons With Confidence - […] The Make Math Moments 3-Part Framework Guidebook […]
- Balancing Practice with Problem-Based Lessons - […] The Make Math Moments 3-Part Framework Guidebook […]
- Teach The Standards To Build Fluency and Flexibility With Number and Operations - […] The Make Math Moments 3-Part Framework Guidebook […]
- How To Teach Algebra: The Distributive Property Progression - […] The Make Math Moments 3-Part Framework Guidebook […]
- Episode 174: Warm-Up Worries - What Should A Warm-Up Look Like? - […] The Make Math Moments 3-Part Framework Guidebook […]
- How To Create Animations For Your Math Lessons - […] The Make Math Moments 3-Part Framework Guidebook […]
- How To Teach The Distributive Property of Multiplication Using Context, Strategies and Models - […] The Make Math Moments 3-Part Framework Guidebook […]
- How To Teach Ratios By Starting With Partitive Division | Scaling In Tandem - […] The Make Math Moments 3-Part Framework Guidebook […]
- Building Multiplication Fluency Through Ratios, Rates and Proportionality - […] The Make Math Moments 3-Part Framework Guidebook […]
- How To Teach Percent To Build Fluency! - […] The Make Math Moments 3-Part Framework Guidebook […]
- Episode 179 - What’s On YOUR Worksheet and How Are You Using It? - […] The Make Math Moments 3-Part Framework Guidebook […]
- How To Teach Algebra: 3 Models For Solving 2-Step Equations - […] The Make Math Moments 3-Part Framework Guidebook […]
- Episode 163: Why Our Existing Resources Need To Change & How To Do It Easily - […] The Make Math Moments 3-Part Framework Guidebook […]
- How Do I Promote Mathematical Models with My Students? - […] The Make Math Moments 3-Part Framework Guidebook […]
- Episode #147:What To Do When You’re Doubting Your Teaching Approach - A Math Mentoring Moment - […] The Make Math Moments 3-Part Framework Guidebook […]
- Two Types of Relative Thinking You Need To Know - […] The Make Math Moments 3-Part Framework Guidebook […]
- Episode 222: Where Math Programs Flourish and Where They Need Support - […] […]
- Episode #224: Kids are Different Now and (What to Do About It) - […] […]
- Episode #225: How Building a Thinking Classroom Can Make Math Moments - […] […]
- Episode #126: My Students Aren’t Engaging and Struggling! What Do I Do? - A Math Mentoring Moment - […] […]
- Episode 182 - How To Reach More Students After Two Tough Years - […] […]
- Episode 192 - How to Use Trickery & Influence In Math Class For Good - […] […]
- Episode #226: What Can I Do When My Students Are Grade Levels Behind? - […] […]
- Episode #227: 3 Act Math Tasks Aren’t Working - […] […]
- Episode 223: Strengthening Your Math Team - A Math Mentoring Moment - […] […]
- Episode 228: How Can I Help My Colleagues Slow Down? - A Math Mentoring Moment - […] […]
- Episode 229: You Have Time For This - Trust Us! - […] […]
- Episode 230: Teaching Math Is Hard. Here's Why... [Part 1] - […] […]
- Episode 231: What Can I Do When My District Feels Stuck? - A Math Mentoring Moment - […] […]
- Episode 233: How to Breadcrumb Your Students Towards Mathematical Proficiency - A Math Mentoring Moment - […] […]
- Episode 234: Making Change Across an Organization When Change Is Hard - A Math Mentoring Moment - […] […]
- Episode 243: [REPLAY] Morphing Your Assessment Practices - A Math Mentoring Moment - […] […]
- Episode #248: How Do I Avoid Burnout and Still Achieve Success - […] […]
- Episode #262: What Are Your Rocks? Discover What Matters Most! - […] […]
- Episode #263: When Calling Parents Isn’t Your Calling - An Interview With Crystal Frommert - […] […]
- Episode #264: Evolving as an Educator: Journey to Demonstrating Mathematical Thinking - A Math Mentoring Moment - […] […]
- Teaching and Learning Math Is Difficult. Here's Why... | Mathematical Thinking - […] […]
- Episode #265: Storytelling and Conceptual Mastery in Mathematics Education with Shayla Heavner - […] […]
- Episode #266: The Pathway To Higher Achievement: A Conversation with Mike Lipnos - […] […]
- Episode #267: Are You Cleaning Up Messes That Haven't Happened Yet? - A Math Mentoring Moment - […] […]
- Episode #268: Can We Build A Thinking Classroom & Still Maintain Rigor - A Math Mentoring Moment - […] […]
- Episode #269: Creating Safe and Equitable Math Classrooms - A Math Mentoring Moment - […] […]
- Episode #270: How To Consolidate & Close Your Building Thinking Classroom Lesson [Part 1] - […] […]
- Why the 9 Times Table Hand Trick Works and How to Teach It Effectively - […] […]
- We Don't Need The Pythagorean Theorem - […] […]
- How To Avoid Death By Webinar - […] […]
- The Easiest Way to Learn New Math Class Strategies & Resources for FREE! - […] […]
- How To Overcome This Common Math Professional Development Paradox | District Math Planning - […] […]
- Why Math Professional Development One-Offs Won't Cut It | Setting District Math Goals - […] […]
- Stop Force Feeding Math Professional Development - Do This Instead | Breadcrumb PD Strategy - […] […]
- Not Enough Time - […] […]
- Your Priorities In Your Math PD Program May Need Shifting - […] […]
- 4 Stages of Mastery - What Teachers Need To Know | MMM Lesson - […] […]
- Episode 216: How To Sow, Cultivate and Foster Your Math Professional Learning Plan - […] […]
- How This Math Leader Stopped Firefighting and Started Leading: A Simple Change For Math Improvement - […] […]
- How To Help Math Teachers Adopt New Teaching Strategies | Math Professional Development - […] […]
- The True Purpose of Assessment in Math Class - […] […]
Submit a Comment
STAY IN THE LOOP:
JOIN THE COMMUNITY
KYLE PEARCE & JON ORR



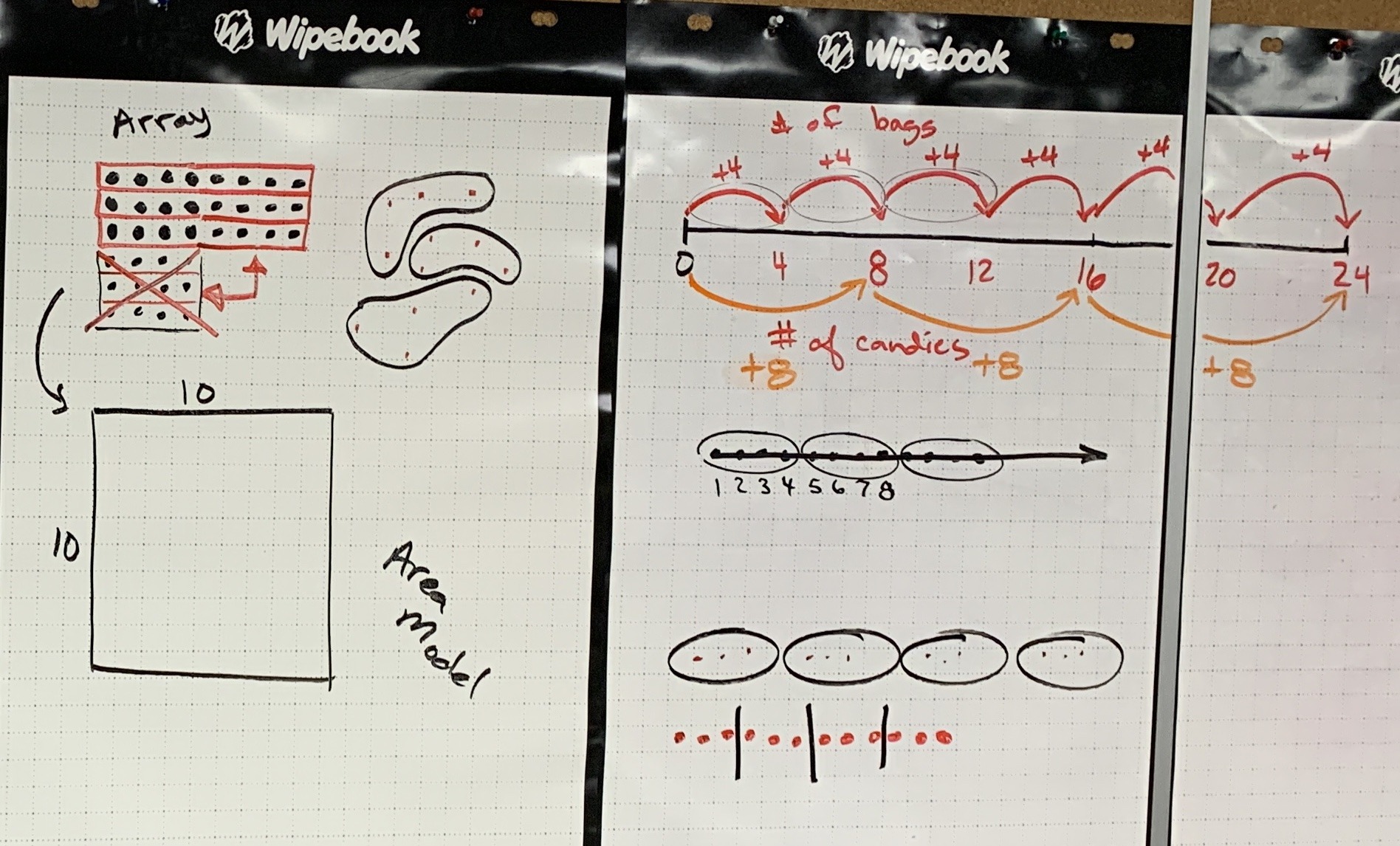

I love this post! Your point that students disengage when they can’t see their thinking in noir models is huge! And I also love that you shared the importance of nudging them to new models but not requiring them to use a certain strategy. When we require whole worksheets of strategies parents rebel against the “common core” or “dumb way of teaching math” or “just teach the way I learned” because we are t using the strategies correctly.
So happy you enjoyed the post. We appreciate the feedback!
You’re so right when it comes to the misconceptions both parents AND teachers have regarding Common Core and what the goal/intention is of many content standards.
Thanks for stopping by!
This is where I am heading with my teaching. I am gratefully learning a great deal on how to “spark” curiousity and then the follow up steps to guarantee learning happens for all. I am curious to find out what app you are using to make your gifs?
So glad to hear it, Mary Alice!
As for the app I use for gifs… typically, it is PicGIF, although Apple Keynote now allows you to export slides as GIFs. Only problem with Keynote gifs is that the files tend to be larger and thus not so helpful for a blog.
Good luck!
With respect… Teaching from an inquiry stance with a constructivist perspective is at the heart of everything you have said….is not new… it’s decades old theory… your ideas and renaming and catch phrases or pretty icons really don’t add anything new to the picture…it’s too bad though it took you this long to figure it out… and I feel embarrassed for those that find any of this new or innovative.
Jason, as an educator with over 25 years of experience, I agree many of these thoughts are not new. But I appreciate the way the article is laid out with supporting details, articles, and examples. It refreshes my thinking about how to help my students to achieve. I would encourage an open mind when reading the article because maybe you can find something to take away. Isn’t that what we want from our students?
I agree that most of this is based on old ideas. What it does do is invigorate the old ideas with some fresh “paint” to make those ideas come to life. The constructive focus needs a revamping from time to time to engage teachers who weren’t engaged before. Jon and Kyle have done a good job in doing that.
We appreciate the comments, Friends.
Our thinking aligns with that of Julie and Ihor as we are not by any means claiming to have created a all of the pieces, however we have spent the better part of the last decade trying to figure out the best way we can put them together on a consistent basis in our own classrooms.
Now, we’re at a point where we feel extremely excited to share these ideas with others.
We feel that there is a need for the Make Math Moments 3-Part Framework because the vast majority of classrooms around the world are still relying on a model built around standing in front of the class and delivering lectures followed by an over-emphasis on memorizing procedures without conceptual understanding. This fact alone should make one realize that we still have a ton of work to do implementing what research has been telling us for decades.
Nice working there and thanks for sharing with us.
“How is it possible that we – two high school math teachers with degrees in mathematics – didn’t realize that multiplying binomials is conceptually the same as multiplying two digit by two digit numbers?”
I have had many students through the years who struggled with the “FOIL” method of multiplying binomials, until I showed them that they could stack the binomials and multiply them just like “regular” numbers, and that the “FOIL” method did the same steps, but looked different. I have also had colleagues tell me that “you can’t multiply binomials like that, you have to use “FOIL”.”
I have been very frustrated as a math teacher, and in recent years as working with blind students in their regular ed math classes. I have often voiced frustration that math is being taught as a series of facts, formulas, and cute sayings to memorize, but there is no building of understanding. Some of the classrooms I’ve been in, I’m not sure the teacher has any understanding of math, either – and one can not teach what one does not understand!
(Listened to a teacher ask students the rule for dividing fractions. When one student hesitantly suggested “multiply by the reciprocal?”, the teacher said, “That’s one way to say it, but the RULE is copy, dot, flip.”)
I am looking to move back into mathematics, and hoping I can work in a school where I am allowed to put your guidance into practice.
Thank you for saying what I have been saying, SCREAMING, for years – to deaf ears.
Thank you for sharing The Make Math Moments 3-Part Framework Guidebook it’s so interesting. It is definitely going to help me transform my teaching of mathematics and help me further ignite the sparks and interest of my students. We all want our students to have the best out come of learning mathematics.
Thanks again for sharing your resource.