Teaching With Problem Based Lessons Through Online Remote Learning

As the entire world has been engaging in emergency remote learning during the COVID-19 crisis, it is likely that you’ve managed to piece together the technology to provide students with new learning through videos available on YouTube or maybe you’ve even created your own. You’ve also worked hard to plan and prepare methods for your students to access practice problems through online tools and digital handouts. 

These are all important and necessary steps to getting your math classroom organized for emergency remote learning, but many educators have felt that there was one important piece missing…

…Moments.

When we lost our ability to facilitate lessons with our students in a face to face environment, we also lost many of our “go to” and almost automatic strategies to Make Math Moments for our students. 

It might even feel impossible to create math moments that your students will remember for days, weeks, months, or even years.

However, we’re here to tell you that It is possible and we want to help you get there. 

Throughout the Spring of 2020, we hosted a series of webinars to help share how we can apply the Make Math Moments 3-Part Framework during emergency remote learning where students were forced to learn synchronously, asynchronously, or maybe even a blend of both. While many of us thought this would be a very short term situation, it sounds like many math classes will be conducted in at least an online blended learning fashion in the Fall. 

While we all know that nothing will ever be as effective as engaging in problem based math learning in a face-to-face environment, this experience is a great opportunity for us to sharpen up our tech skills and think of ways that we might use them to enhance our lessons once we’re back in our classrooms learning “in the flesh”.

Our Make Math Moments From A Distance Webinars received such a positive response that we took the replays and built out a course inside of the Make Math Moments Academy for Math Moment Makers to enjoy at their own pace (and free for 30 days).

In this post, we intend to summarize some of the key learning objectives we shared for those who participated in our Make Math Moments From A Distance webinars including:

• How to deliver problem based lessons in a meaningful way;
• How to reach all students regardless of their mathematical readiness through the use of emerging mathematical strategies and models; and, 
• How to deliver engaging lessons over the internet synchronously or asynchronously.

While we tend to use examples that best suit Grades 3 through 10, the big ideas can be utilized to help up your Make Math Moments game as we lead problem based lessons that Spark Curiosity, Fuel Sense Making, and Ignite Your Teacher Moves from a distance.

Now, if you’ve never come across the Make Math Moments 3-Part Framework, we suggest that you click here before moving on to get a thorough understanding of the 3 elements that we believe have a huge impact on making math lessons that are memorable and create resilient problem solvers. Throughout this post, we will summarize how you can still utilize the elements of the framework to Make Math Moments From A Distance.

1. Spark Curiosity

Each Make Math Moments problem based lesson or unit must begin with a Spark; something to pique curiosity and wonderment. While there are many different ways to Spark Curiosity, we have analyzed many of the different ways commonly used be it 3 act math tasks, contextual problems, rich tasks, or even just math puzzles, most tend to follow what we call The Curiosity Path.

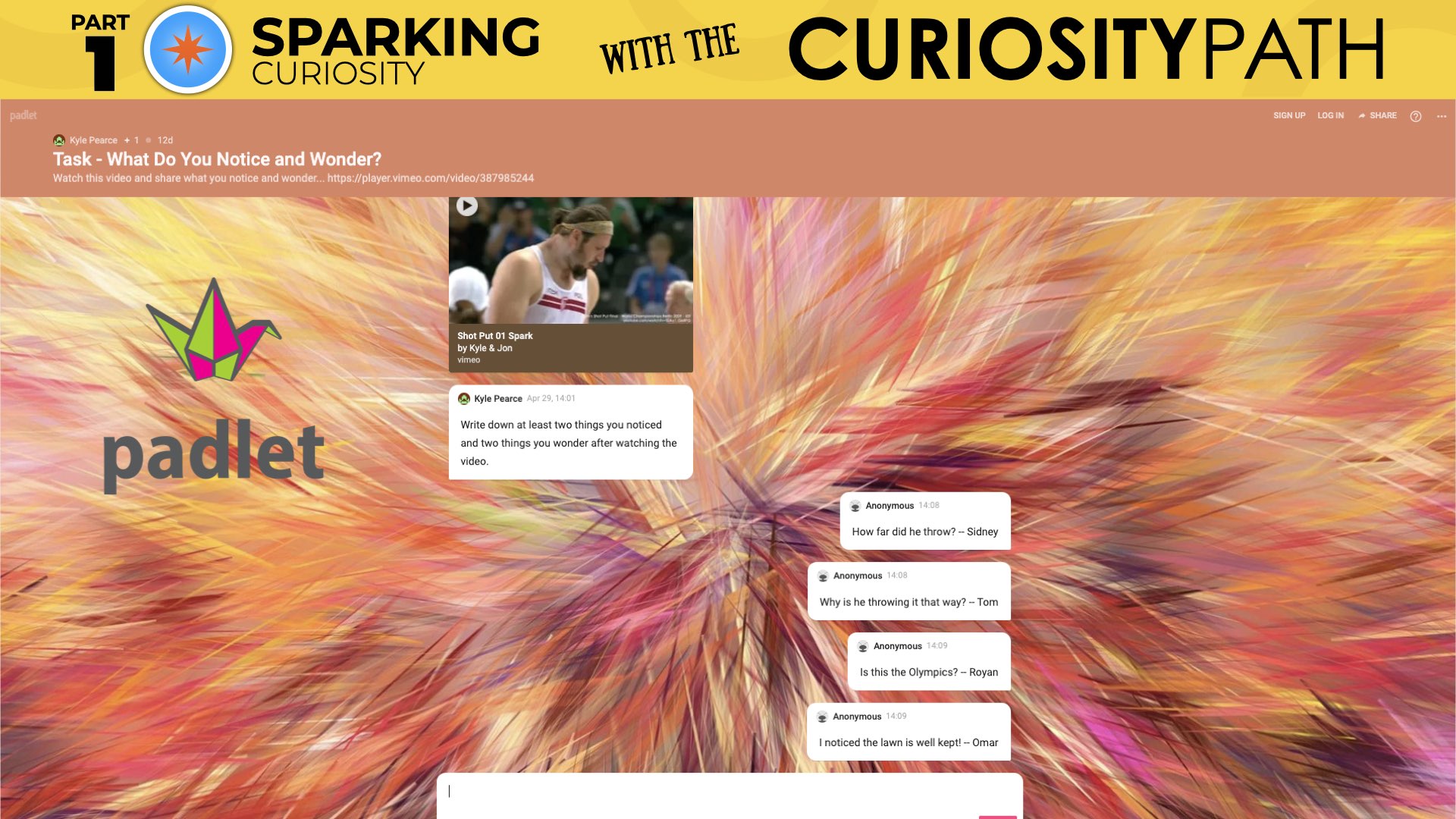
In one of our Make Math Moments From A Distance webinars, we used Day 1 of our Shot Put problem based unit to help us model the process synchronously by first by asking participants to watch this video and write down anything and everything they noticed and wondered in the chatbox.

Here’s some examples of the noticing and wondering that was shared in the chatbox:

• I notice a stadium.
• I wonder how much the shot put weighs?
• A shot put was thrown.
• That was far.
• How many people are in the audience?
• I wonder how far he threw it?
• And many others…
• Take time to acknowledge the noticing and wondering your students have engaged in and try to answer any that you can address right away.

We then land on the following prompt:

How far did he throw the shot put?

Just as we would ask students to turn to their peers in a face-to-face learning environment and make an estimate, we asked the educators in the webinar to make an estimate and share it synchronously in the chat.  

What we found in our live webinar as well as what you might also find with your own students is that the estimates shared often have many different units of measure since we did not specify one. 

What a fantastic learning opportunity!

By leaving the estimate initially open – by not specifying the unit of measure – we can listen and learn about our students. Not only can we get a sense of how familiar they are with the shot put event, but we can also learn about what standard measurement units they are familiar with and an understanding of their own sense of magnitude when working with that unit of measure.

To allow us to better compare the estimates across the larger group, we shared the following image offering up a non-standard unit of measurement to keep the floor very low:

After students share out their estimates live in the chatbox, we could then utilize a digital manipulatives tool like the Number Lines tool from Brainingcamp.com to help us honour student voice and give us a sense of the range of estimates as well as the central tendency of the estimates.

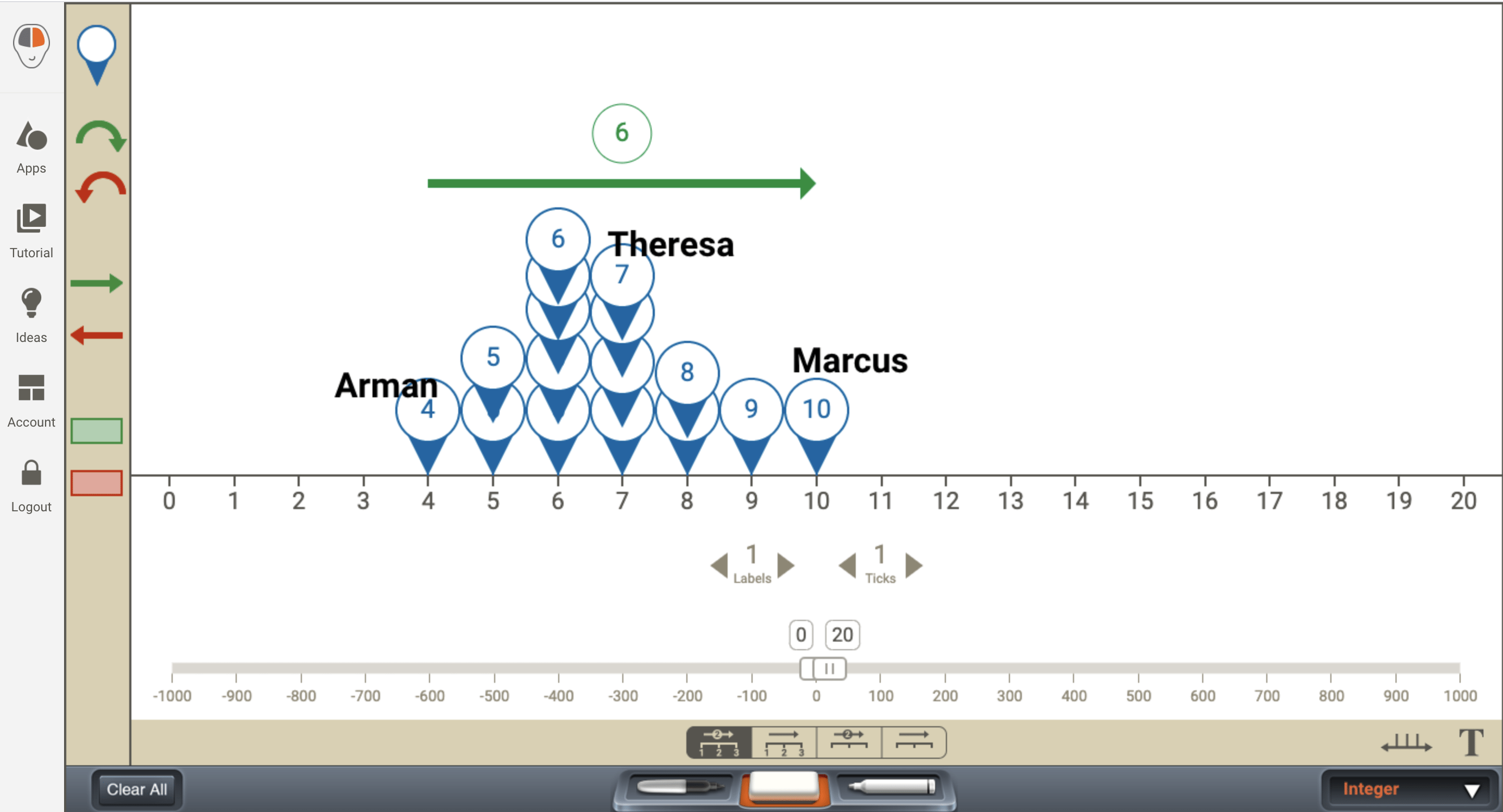
At this point, we should pause and reflect on what has taken place. 

The lesson to this point has been focusing specifically around Sparking Curiosity through the Curiosity Path. 

Pause for a moment and try to jot down what intentional moves we’ve made to this point to shape the path for curiosity.

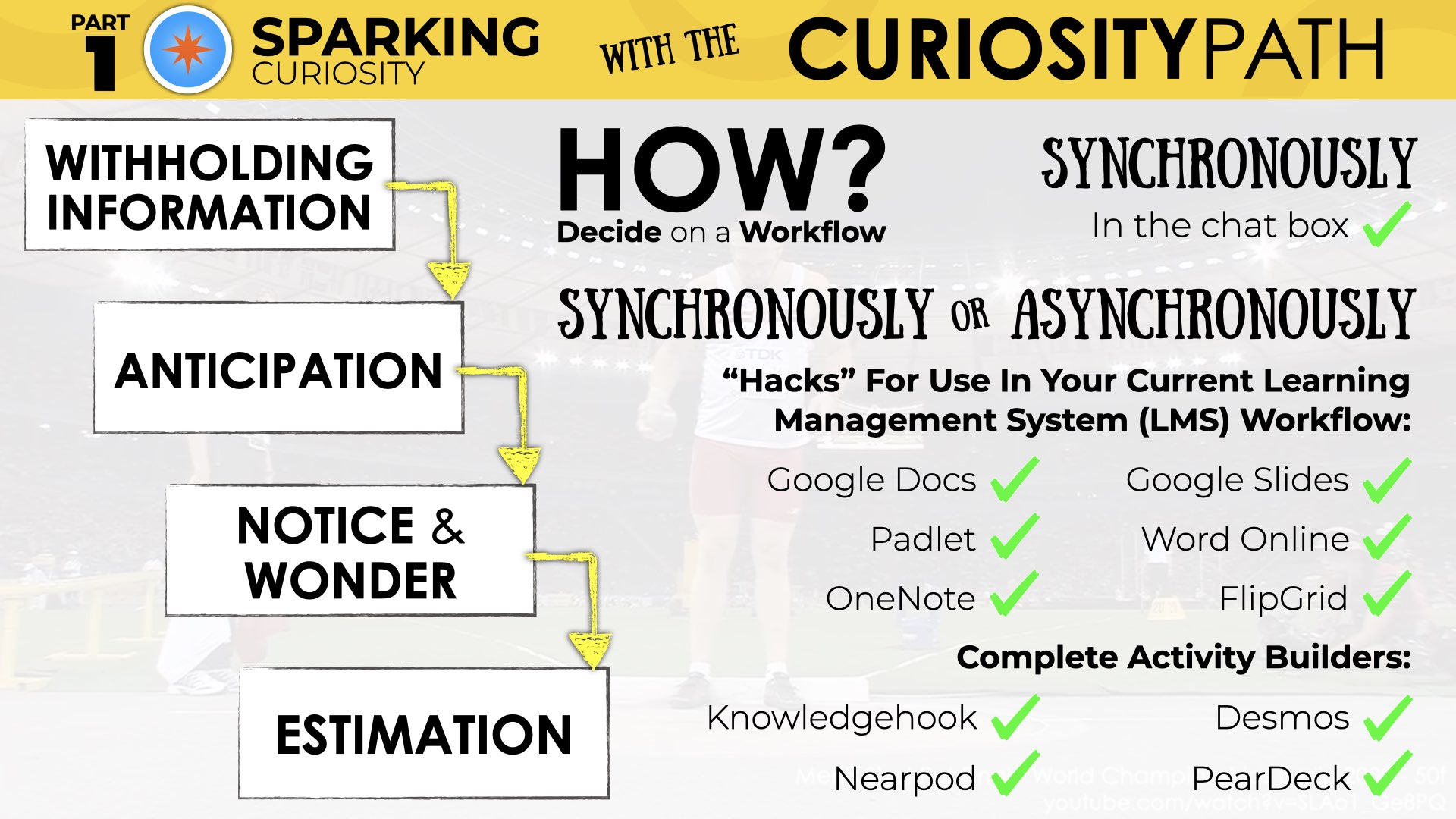
Sparking Curiosity Through The Curiosity Path

The idea behind the Curiosity Path may seem simple, but it is also very easy to overlook.

The intentional moves we make to shape the Curiosity Path to make a memorable math lesson include:

1. Withholding Information
2. Build Anticipation
3. Notice and Wonder
4. Estimate

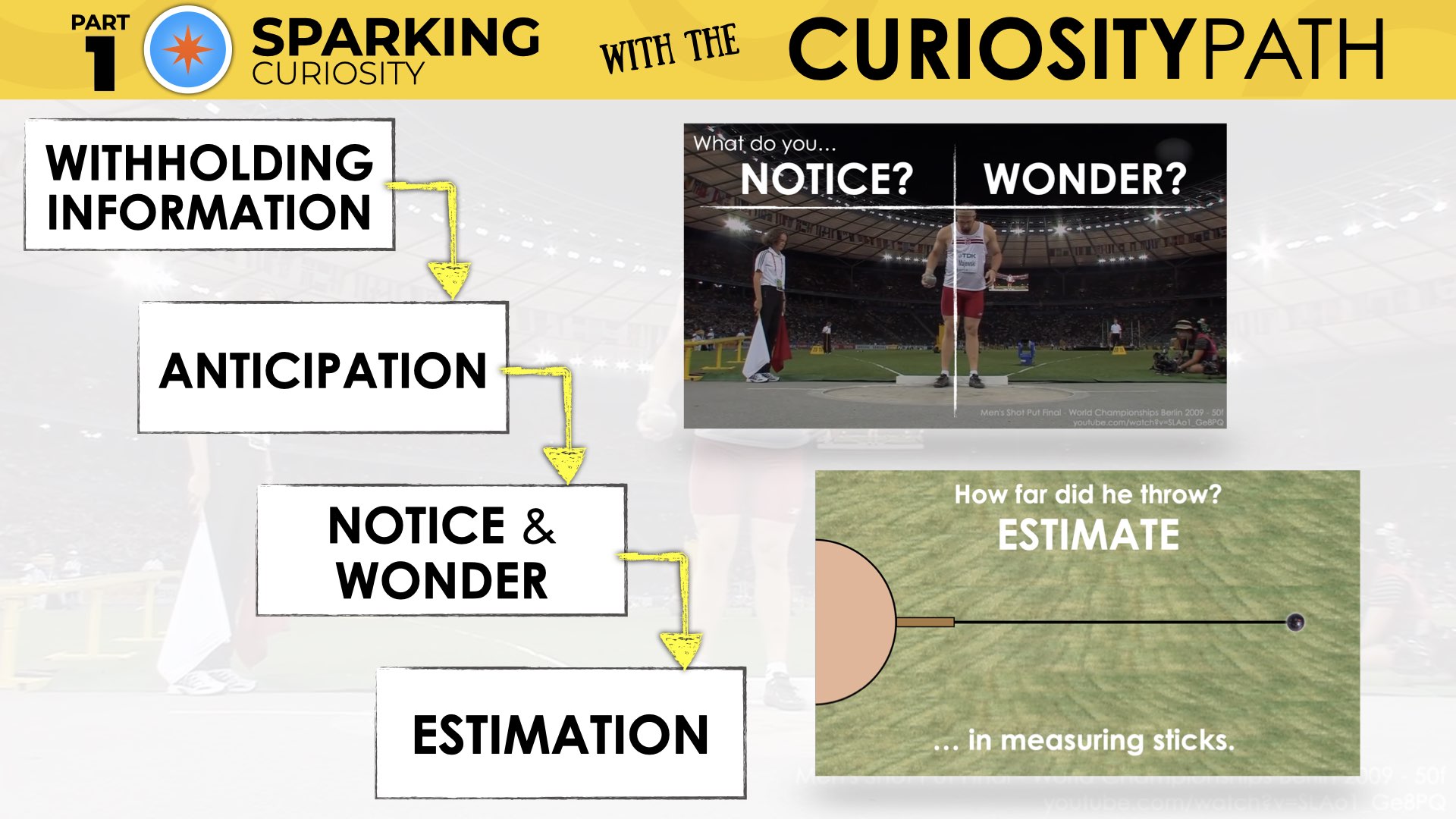
To this point in the Day 1 lesson of the Shot Put problem based unit, we’ve withheld a significant amount of information with the goal of building anticipation.  

How did we do it? 

In this case, we simply shared a video of an athlete throwing a shot put and asked students to jot down what they notice and wonder. 

A Word Of Caution:

While it might seem like the first three moves in the Curiosity Path are individual elements, they are so tightly connected that they must be planned and implemented in tandem. If we fail to withhold enough information to create enough anticipation, we risk a higher chance that our notice and wonder protocol will come out flat. 

At this point, many are often left wondering how they can most easily get started implementing the Curiosity Path in their blended or fully online distance learning lessons whether they are led synchronously or asynchronously. It might seem difficult or overwhelming at first, but we have some easy ways to get yourself started.

Sparking Curiosity From A Distance With The Curiosity Path

If you’re reading this blog post right now, my guess is that you’re a pretty eager educator. Unfortunately, that also means that you’re probably the type of person who likes to do things themselves and gain the satisfaction of customizing things more specifically for your own group of learners and your own teaching style. 

This certainly isn’t a bad thing when it comes to being the best math educator you can be, but it can make it harder when trying to transform your practice from say a more traditional “I do, we do, You do” model of instruction to a problem based approach like we promote to Make Math Moments.

So rather than trying to create problems that Spark Curiosity from scratch, we’d recommend starting with readymade tasks such as our Make Math Moments Problem Based Lessons & Units or use our Curiosity Search Engine to help you find other tasks that have been shared by many great math educators on the web. Best of all, our tasks have been designed specifically with the Curiosity Path in mind, while most of the tasks you’ll find via our search engine have the path pretty well shaped for you requiring just some minor considerations and/or tweaking to suit.

Of course, we’d never want to hold you back from creating your own. If you plan on doing this, consider tasks you would typically use from say your textbook, current lesson plans, or teacher resource guide and use the Curiosity Path to help you transform them into curious tasks rather than starting from nothing.

What About Sparking Curiosity Asynchronously?

To this point, we have been sharing what leading a Make Math Moments problem based lesson could look like in a synchronous learning environment. For the educators who have had the pleasure of teaching during emergency remote learning, you’ll know that regardless of whether you’re willing and able (i.e.: district will allow) the delivery of synchronous online lessons, in many cases class attendance is not nearly as high as it was when teaching face-to-face.

While a synchronous experience will be more rich and interactive, we can still provide an opportunity to shape our asynchronous lessons using the Curiosity Path.

Decide On A Workflow

It is important to decide on a workflow that will be most effective for you and your learners. 

A great place to start is by trying to leverage the tools that your school district currently supports. If your school district is a G Suite for Education district, then honing in on tools like Google Classroom, Google Docs, Google Meet, and JamBoard seem like great places to start your planning. If your school district is an Office 365 district, then exploring tools such as OneNote, Word Online, Teams, and Flipgrid seem like places to take a deep dive. Of course you’ll probably find that one platform alone won’t satisfy all of your needs, but you mind as well begin working with the tools that your district approves and can offer you support in.

For example, if your district is a Google district or you’re an avid Google Apps user like us, you could create a simple shared Google Doc to honour student voice via the Notice and Wonder protocol:

Or, maybe you’ve used Padlet in the past and really enjoy how visually appealing as well as how quick and easy it is to set up a new Padlet wall, then you could definitely go that route.

Maybe you’re thinking that you’ll get a better response if students are able to easily record and send you short video clips sharing their thinking. In that case, maybe FlipGrid is the way you might choose to go?

The key to remember is that the tech tool you choose isn’t the most important part; following the Curiosity Path is. So whatever you choose to best re-create the flow of a synchronous lesson for your asynchronous learning experience is completely up to you and your comfort level. Try to select as few tech tools as you can to get you the end result you’re after.

Spark Curiosity With These Tech Tool “Hacks”

Regardless of what Learning Management System (LMS) you and your district is using or whether you’re leading your learning synchronously, asynchronously, or both, here are some great tools that you can use to “hack” your workflow.

• Google Docs
• Google Slides
• Padlet
• Word Online
• OneNote
• FlipGrid 
• And many more…

Let’s also not forget that if you’re “live” with your students, then the chatbox is often a great spot for recording details from the Spark portion of your lesson like what students notice and wonder as well as their estimates.

Spark Curiosity With Complete Activity Builders

For some educators, “hacking” your way through your synchronous and asynchronous math lessons is not sitting well in your stomach. 

No fear. 

In our Make Math Moments From A Distance follow-up webinars, we took some deep dives into complete activity builders such as Knowledgehook and Desmos to show how you could build your entire lesson within platforms such as these to eliminate all of the moving parts that using some of the “hack” tech tools above might require of you. 

If you’re interested in taking that deep dive, check out Modules 3 and 4 of the Make Math Moments From A Distance Academy course. We may still have a free month trial available which should be more than enough time for you to gobble up all of that learning. You can learn more about taking that course for free here.

Here’s a list of some great math activity builders that we’ve used in the past and continue to use currently:

• Knowledgehook
• Desmos Activity Builder
• NearPod
• PearDeck
• And many others…

Now that may seem like a lot of effort focused on Sparking Curiosity during our math lessons – and you’d be 100% correct.

Regardless of whether we are teaching face-to-face, in a blended, or fully online learning environment, we need to ensure that we are getting our students to lean in during our math lessons; not just because they “have to”, but because they are truly interested in answering the wonders that have been brought to the forefront. 

This idea isn’t new, but we’d argue that now more than ever do we need to spend a significant amount of time building our mathematics community of learners and engaging students to continue learning with us. You won’t find any educator stating that distractions weren’t a problem when we were teaching face-to-face. Well, the influence of those distractions increased drastically as soon as we had to shift learning to an online environment where students are engaging from home. 

If we are unsuccessful at sparking curiosity with our students early and often, we risk more students disengaging with each passing day.

2. Fuel Sense Making

Now that we’ve taken time to Spark Curiosity using the Curiosity Path and we’ve honoured student voice, it is time to give students their first challenge while still keeping the floor relatively low to ensure all can access this task.

How are we going to do it?

Well, we’re going to start giving students a bit of information that we had withheld initially.

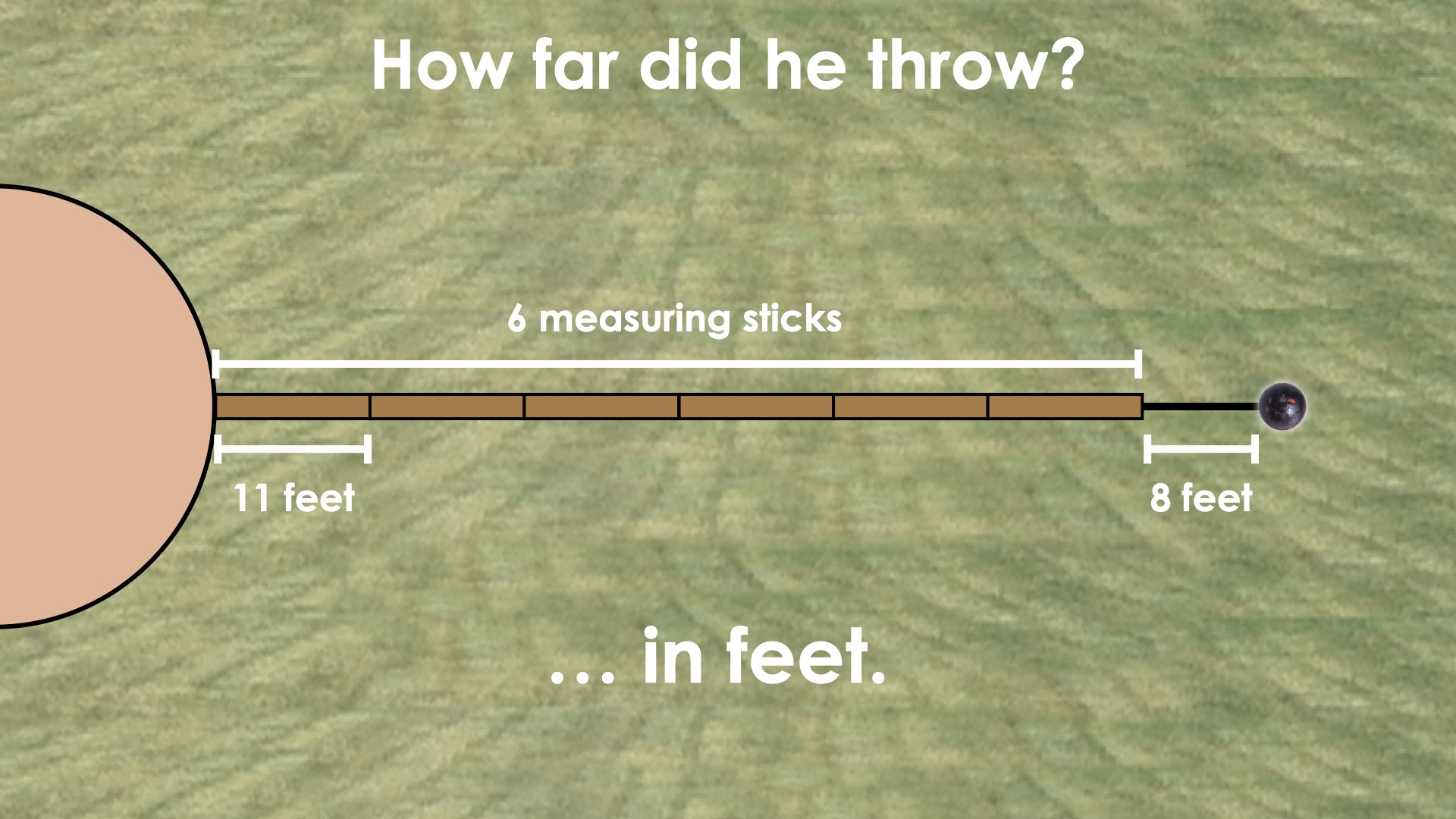
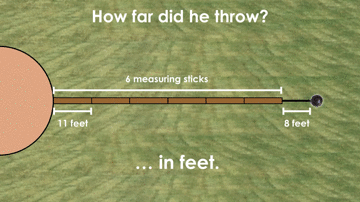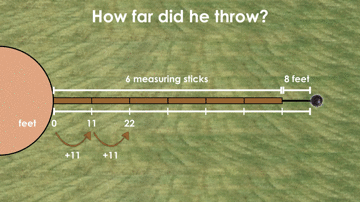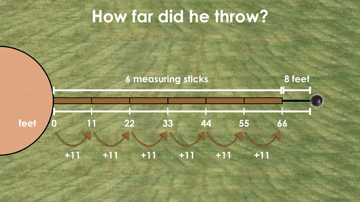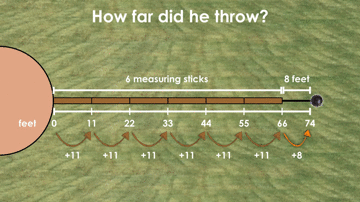
We’ll show students that the official measuring the distance of the throw used 6 of these brown measuring sticks plus she had to pace out an additional 8 feet to reach the landing point of the shot put.

Sharing with students that the graphic is to scale, you could consider asking students to update their estimates in “brown measuring sticks”. 

This might prompt students to use fractional thinking with estimates like 6 and 3 fourths or 6 and 4 fifths of a measuring stick. Some students might resort to using the decimal system, while others might share a more general “just short of 7 sticks”.

We could also prompt students to try and update their estimate using feet as their unit of measure. 

If a brown stick is longer than 8 feet, what might you estimate the length of each brown measuring stick to be? Can you use this to help you estimate the length of the throw in feet? 

So many options here for purposeful questioning in order to Fuel Sense Making.

After honouring student voice, we can then reveal to students that the actual length of each brown measuring stick is 11 feet and off to work they’ll be.

How intuitive it will feel to so many students when they access the task through the approach that matches their individual entry point. 

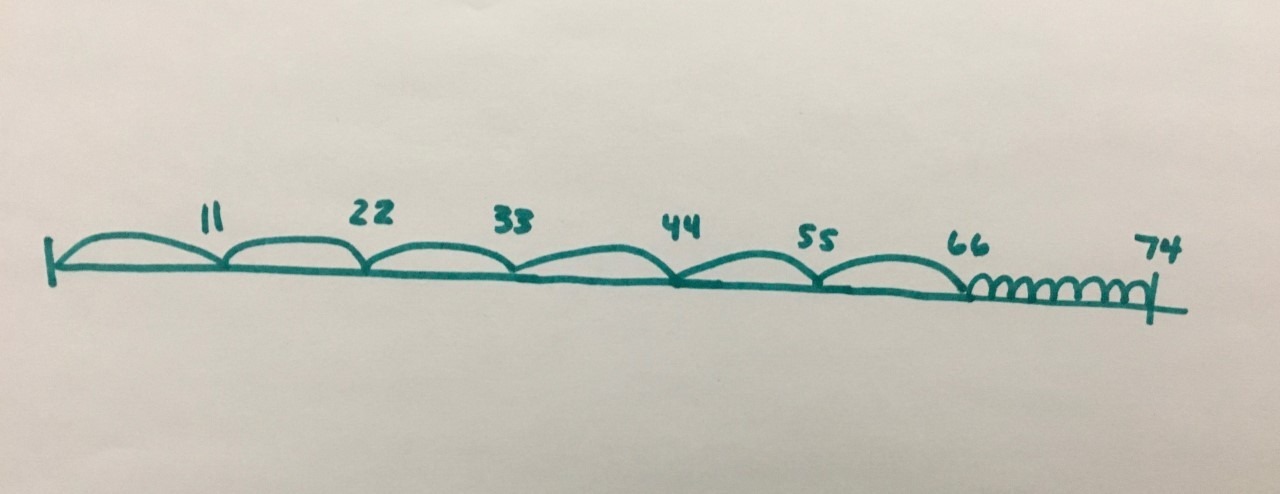
For example, some students might skip count by 11 feet on a number line to model the situation similar to the image above, and then adding on the additional 8 feet:

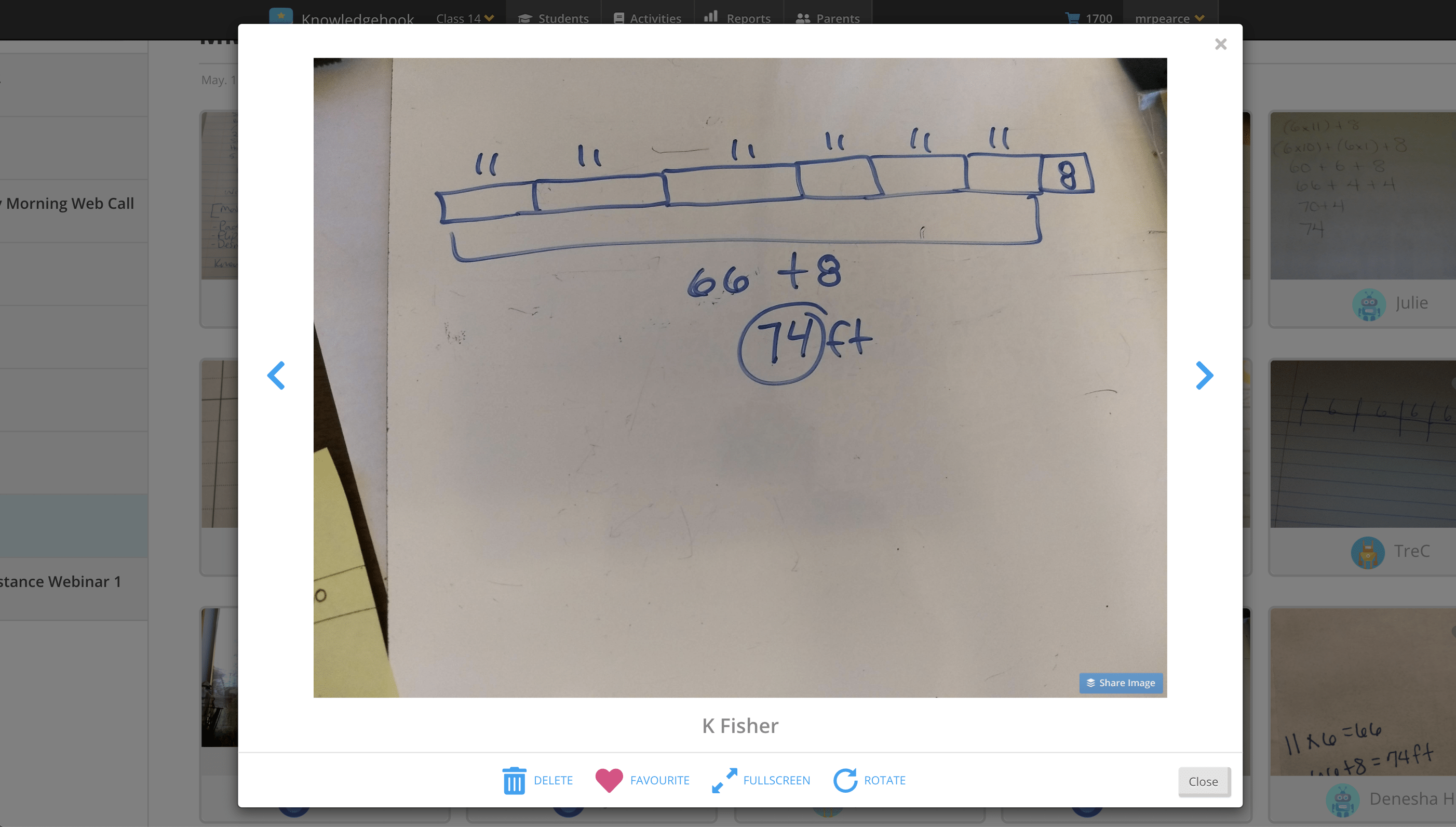
Other students might apply a partial products strategy as they flex their distributive property of multiplication over addition muscles like this student did here by multiplying 6 groups of 10 feet first, then adding an additional 6 groups of 1 foot for a total distance of 66 feet for the measured sticks and then adding the additional 8 feet for a total of 74 feet:

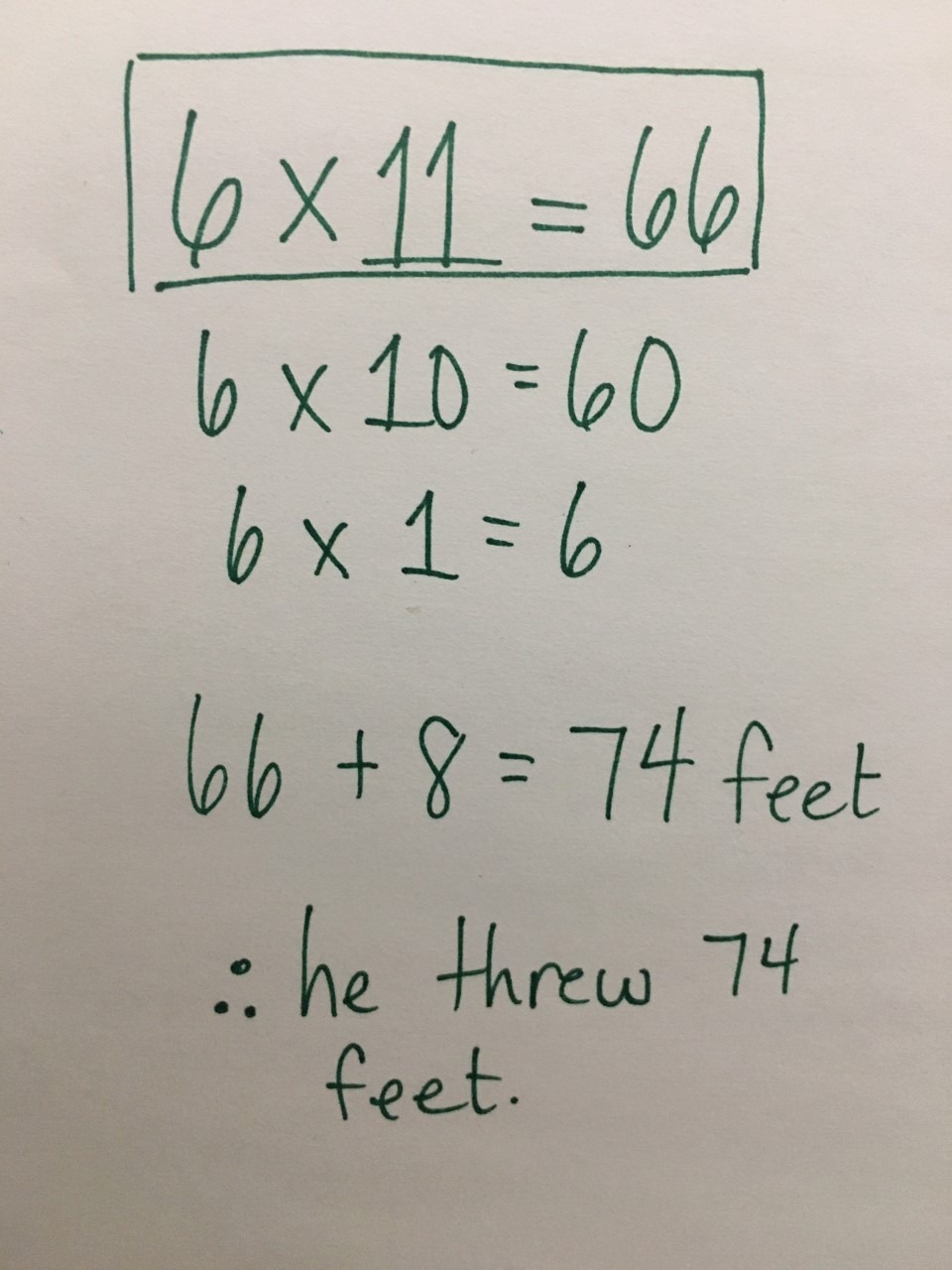
Or, maybe this student immediately sees the 6 iterations of 11 feet and the additional 8 feet as an expression of 6 groups of 11 feet plus an additional 8 feet all in one step:

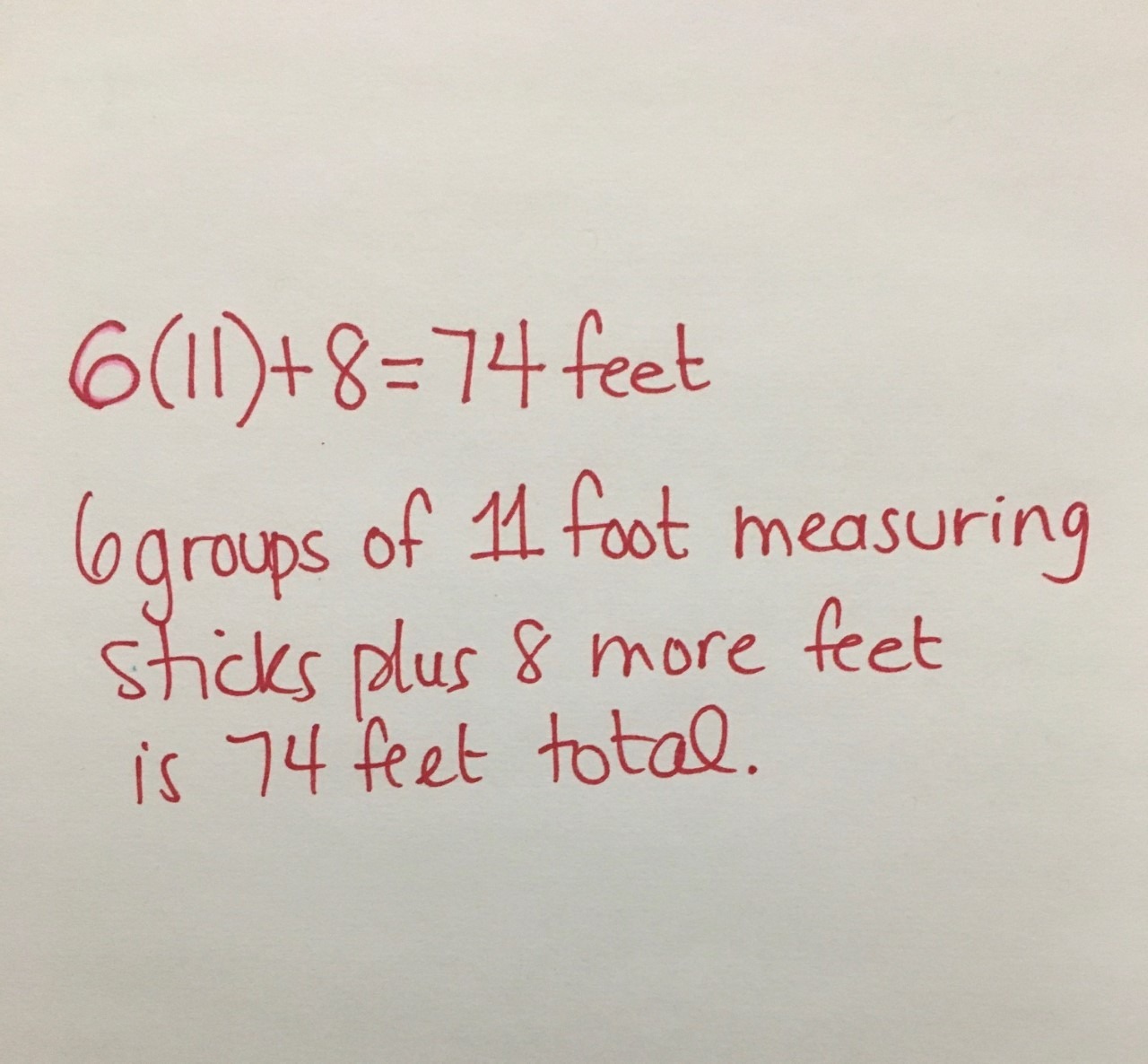
Of course there are many other possible student approaches that may arise, but by giving students the opportunity to productively struggle by attacking the problem with a strategy and mathematical model that they feel comfortable with, we are now setting ourselves up for an opportunity to create an effective and intentional consolidation of the learning.

How To Craft Math Moments That Fuel Sense Making

If you’re like us, your own experience learning mathematics in school might have sound a lot like “I do, We do, You do” and it can be hard to shake that approach from our minds when planning and delivering math lessons.

With a Make Math Moments problem based math lesson, we are flipping that model more to a “You do” first, then as the facilitator, we are helping students make connections by starting with student thinking.

Unfortunately, it can be really easy to do too much telling in our lessons when we should be asking more questions and staying curious with our students.

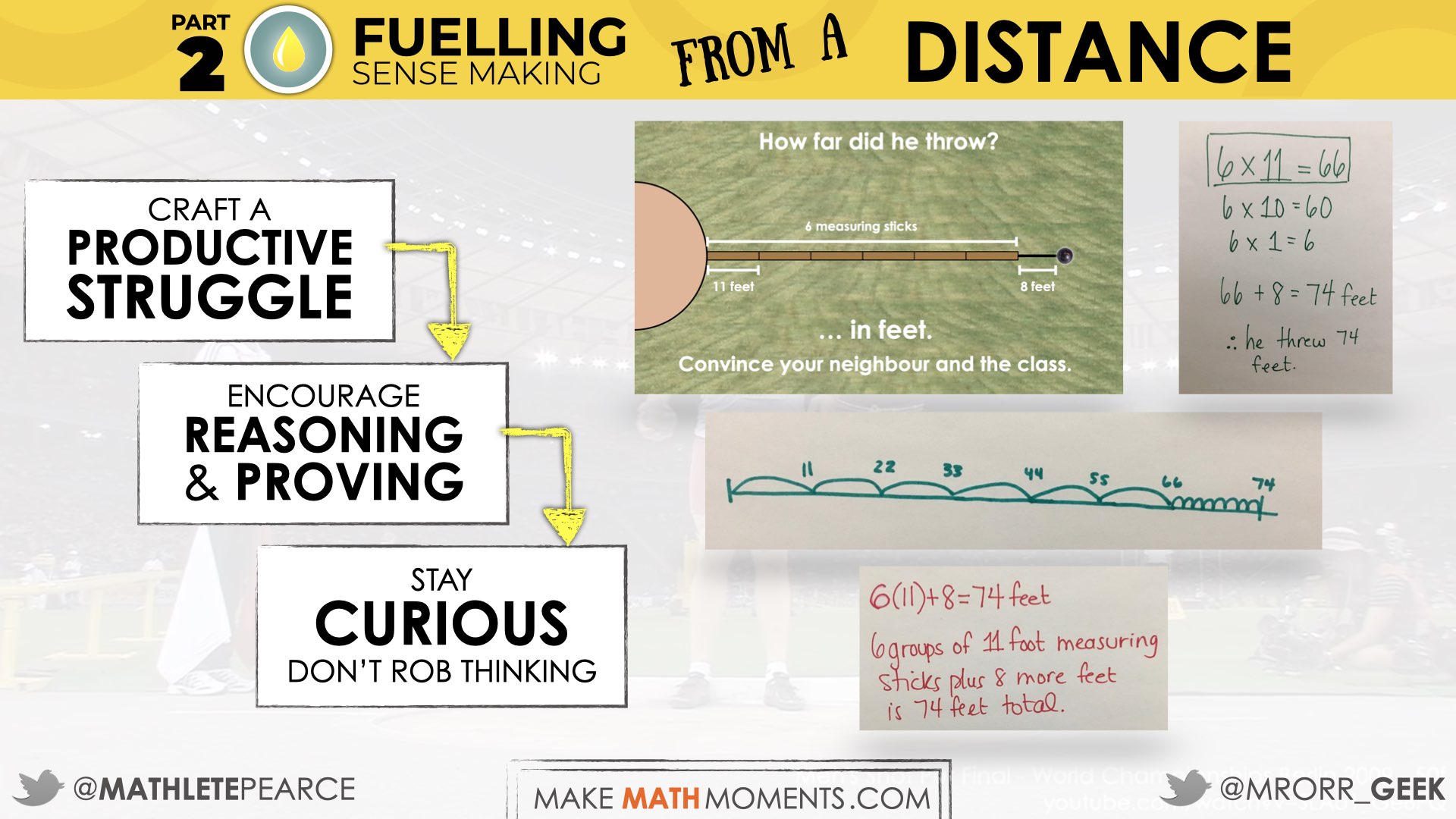
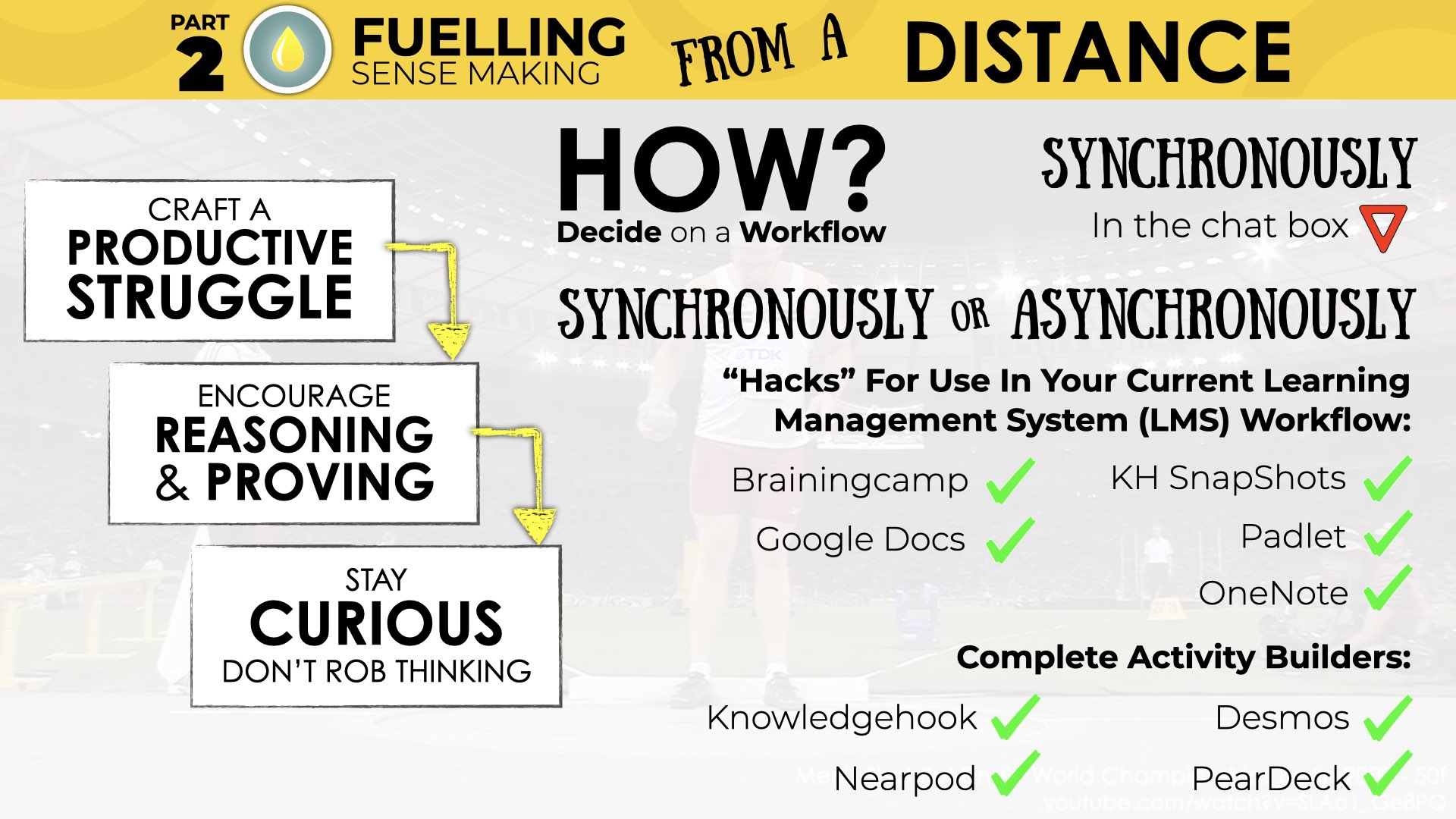
As we plan and deliver our math lessons, we want to be sure that we:

1. Craft a Productive Struggle
2. Encourage Reasoning and Proving
3. Stay Curious to Avoid Robbing Students of their Thinking

While it is easy to write down the list above, it is much more difficult to try and put these very important elements into practice especially if leading problem based lessons is not what you’re used to. 

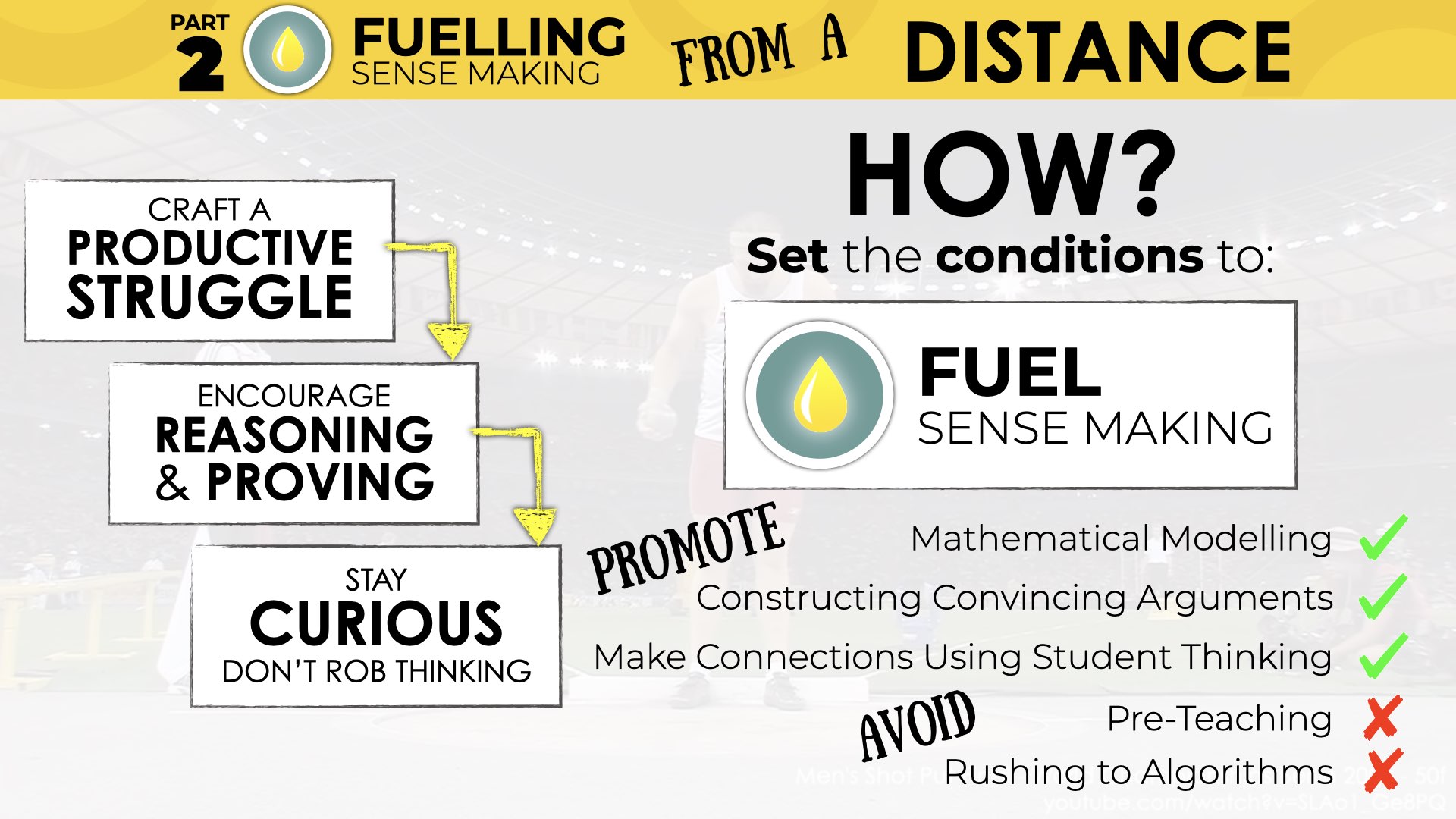
So let’s discuss some of the conditions that we can create in our math classroom to make these ideas more implementable.

Setting Conditions to Fuel Sense Making

Crafting a productive struggle begins with giving students a problem worth solving. Often times, these are contextual problems and following the Curiosity Path as a start and then ensuring that the information and quantities you will eventually share with your students provide for a rich mathematical experience. In order to preserve the curiosity you have worked so hard to spark and to ensure a true productive struggle is crafted for students, we must also resist the urge to pre-teach students; again, a very difficult thing to do if you’ve been teaching for many years with a “procedures first” mindset. 

Encouraging reasoning and proving in your Make Math Moments Problem Based Math Lesson can only be achieved if students are encouraged to come at the problem using their own approaches. This means students will be accessing the task utilizing strategies and models that have emerged in their past mathematical experiences – some likely picked up from your class, while others may be those that they have built the trust to use and depend on over many months or even years. Unfortunately, if students have had little or no experience engaging in problem based lessons where mathematical strategies and mathematical models are promoted and developed over time, be ready for having to meet students where they are and slowly build up their fluency and flexibility with both strategies and models. While this might feel daunting, know that it is so worth it and you will see students excitement for mathematics quickly come alive.

Something else you’ll notice with problem based math lessons is that the end goal isn’t just an accurate or precise answer. Our goal is prompting and pushing students to construct convincing arguments that help to share their approach and perspective of the problem. Here we are less concerned about whether the answer they came up with is right or wrong, but rather to push them to communicate their approach and slowly build a group of fellow mathematicians in the classroom to support their thinking. If they’re right, they will eventually be able to convince their peers. If they’re wrong, then a (friendly) math fight will ensue until one side eventually is convinced by the other. From these mathematical conversations, students are able to make connections between their work and the work of others in the classroom. 

But, beware: all of this is not possible if we pre-teach students what “we” perceive to be the most effective and/or efficient strategies and if we leave concrete and visual mathematical models behind in a rush to the algorithm.

This is how we Make Math Moments That Matter for all of our students and Fuel their Sense Making during each problem based lesson.

Tech Tools to Fuel Sense Making Both Synchronously and Asynchronously

While the chat feature in many different video conferencing software platforms are helpful to engage with students in a synchronous fashion for typing text back and fourth, some of them may not be ideal for trying to fuel sense making. 

This might mean leveraging some of the tools mentioned previously in this article, or possibly another that best suits crafting that productive struggle and pushing students to reason and prove.

One tool that is helpful both for students to leverage digital math manipulatives that are robust and easy to use is Brainingcamp.

With Brainingcamp, you have a great lineup of tools that make mathematical modelling in a digital environment as convenient as possible. We should also note that In some cases, digital math manipulatives can sometimes do what is possible with concrete manipulatives or pictorial math models. 

While Brainingcamp is a paid premium tool, they often have trials for teachers to try them out.

When it comes to having students just productively struggling away on paper or, if available, non-permanent surfaces like chalkboards or whiteboards, sometimes snapping a photo and having an easy place to share it might be the way to go. 

Again, we could resort to some of the tools we shared previously, or you might consider leveraging the power of Knowledgehook’s FREE SnapShots tool.

With Knowledgehook SnapShots, you can quickly open up a SnapShots “Session” where a screen is shared prompting students with instructions of how to upload their solution strategy.

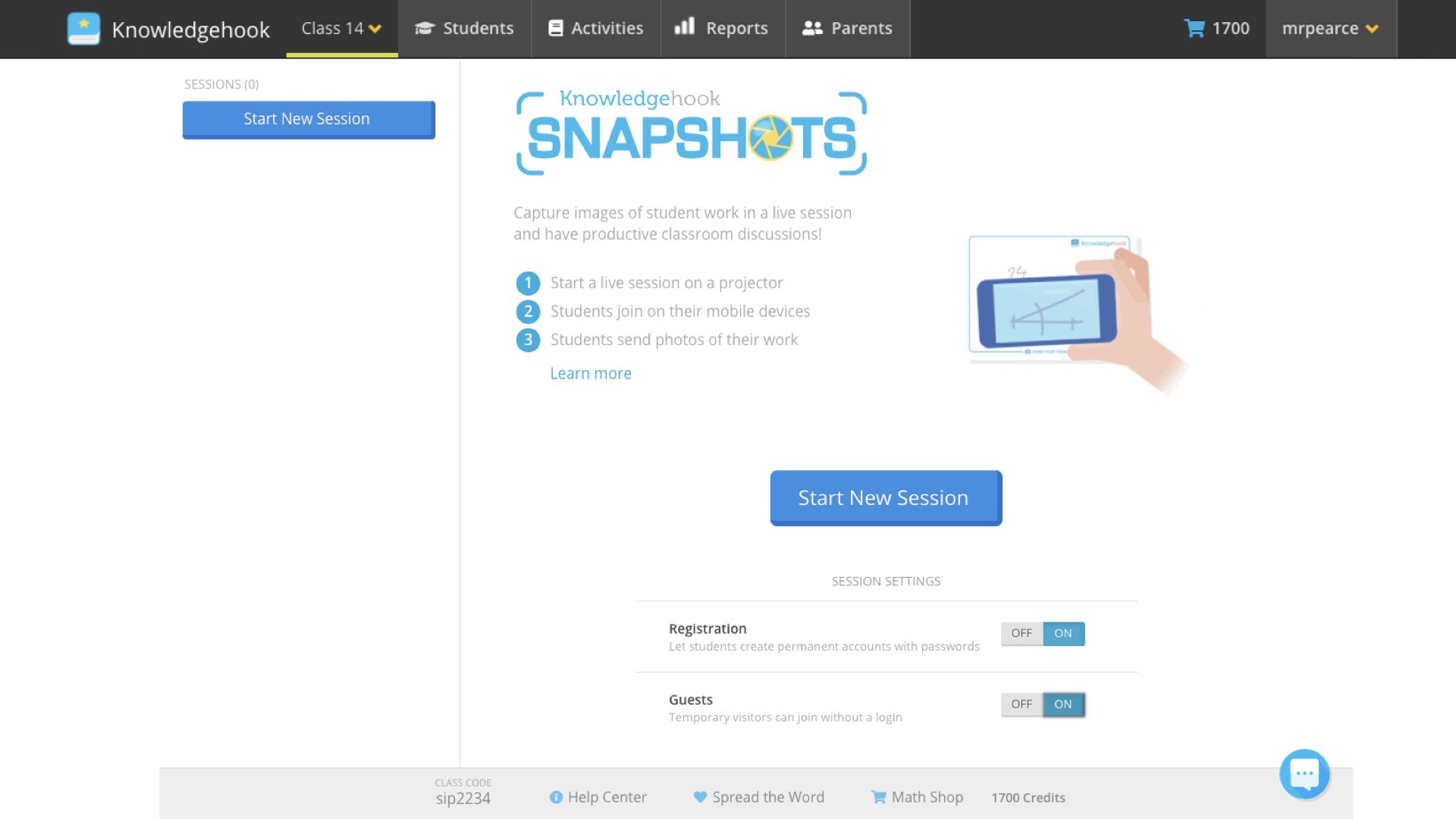
For example, when I started a session for one of our Make Math Moments From A Distance webinars, students were prompted to visit joinkh.com and enter my unique class code sip2234.

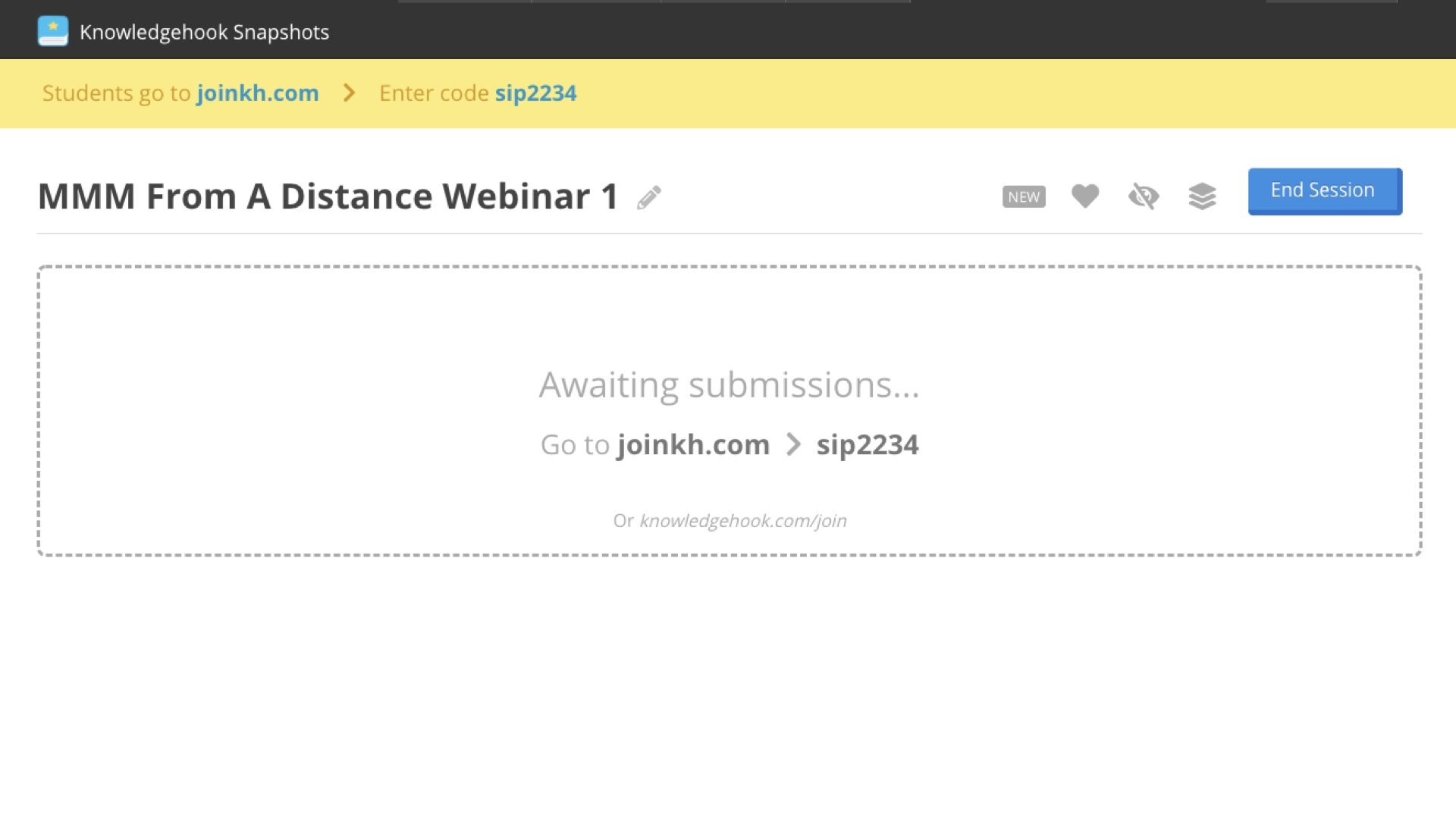
Students will then be asked to use their Knowledgehook account to login (if they have one), register for an account, or if toggled by the teacher, simply logging in as a “Guest”.

At this point, students will have only one button on their screen that will allow them to turn on the camera on their device or to access the photos on their computer/phone/tablet. Submit the photo and within seconds, the teacher will see the solution that can now be leveraged for making connections during consolidation.

Clicking on any image will enlarge it for you to display to the class when the time comes for consolidation and making connections.

This tool is something that we here at Make Math Moments had been asking the Knowledgehook DevTeam to create for quite some time. It is great to see it out and a bonus that it is free for teachers to use and access.

All you have to do to access the free tool is sign up for a free Knowledgehook teacher account.

Here is a list of just a few of the tech tools you might consider using to help you Fuel Sense Making in your students from a distance both synchronously and asynchronously:

• Brainingcamp
• Knowledgehook SnapShots
• Google Docs
• Padlet
• OneNote
• And many more…

All of the complete math activity builders we recommended for Sparking Curiosity are also extremely helpful for Fuelling Sense Making at a distance:

• Knowledgehook
• Desmos Activity Builder
• NearPod
• PearDeck

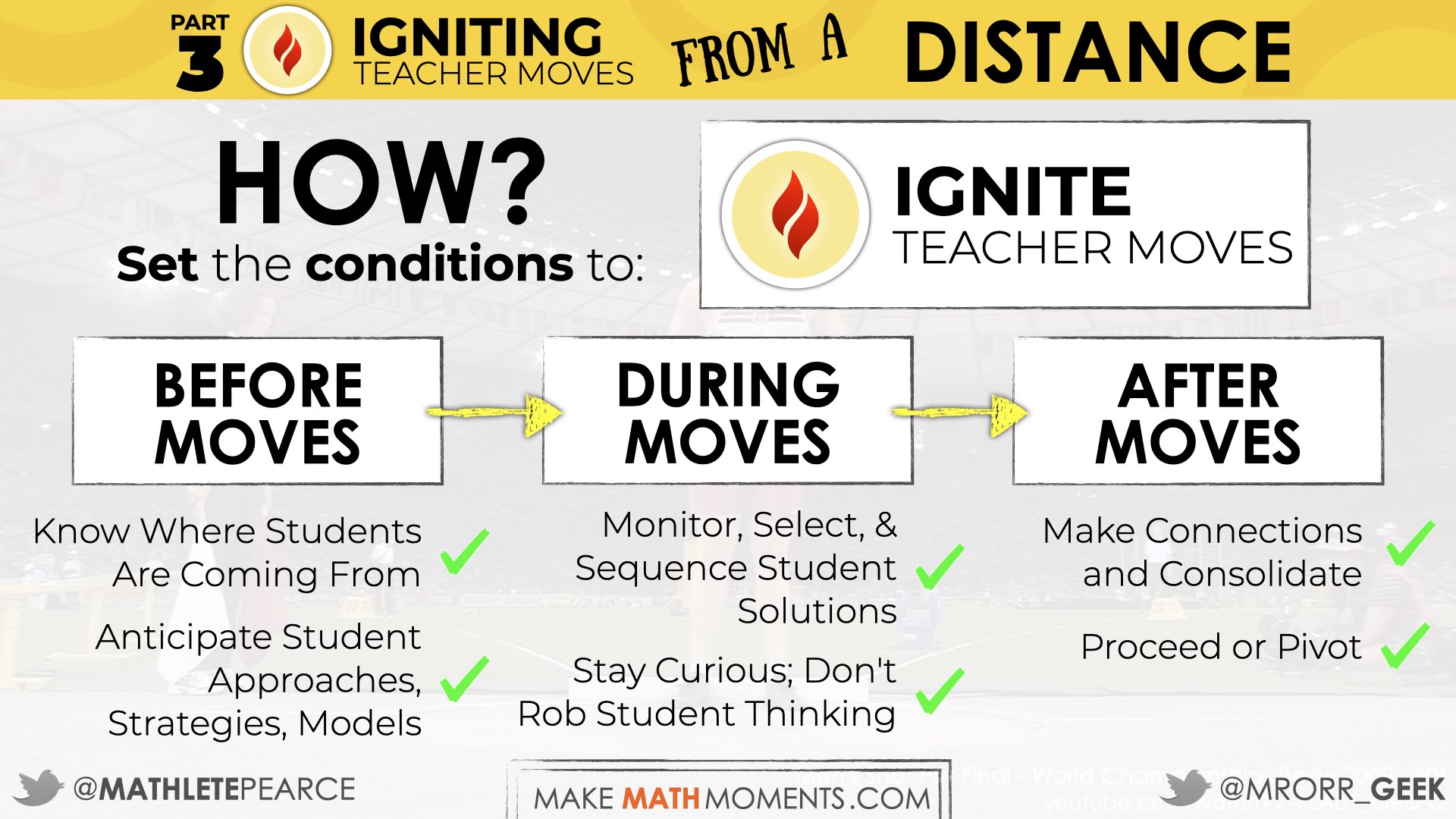
3. Ignite Teacher Moves

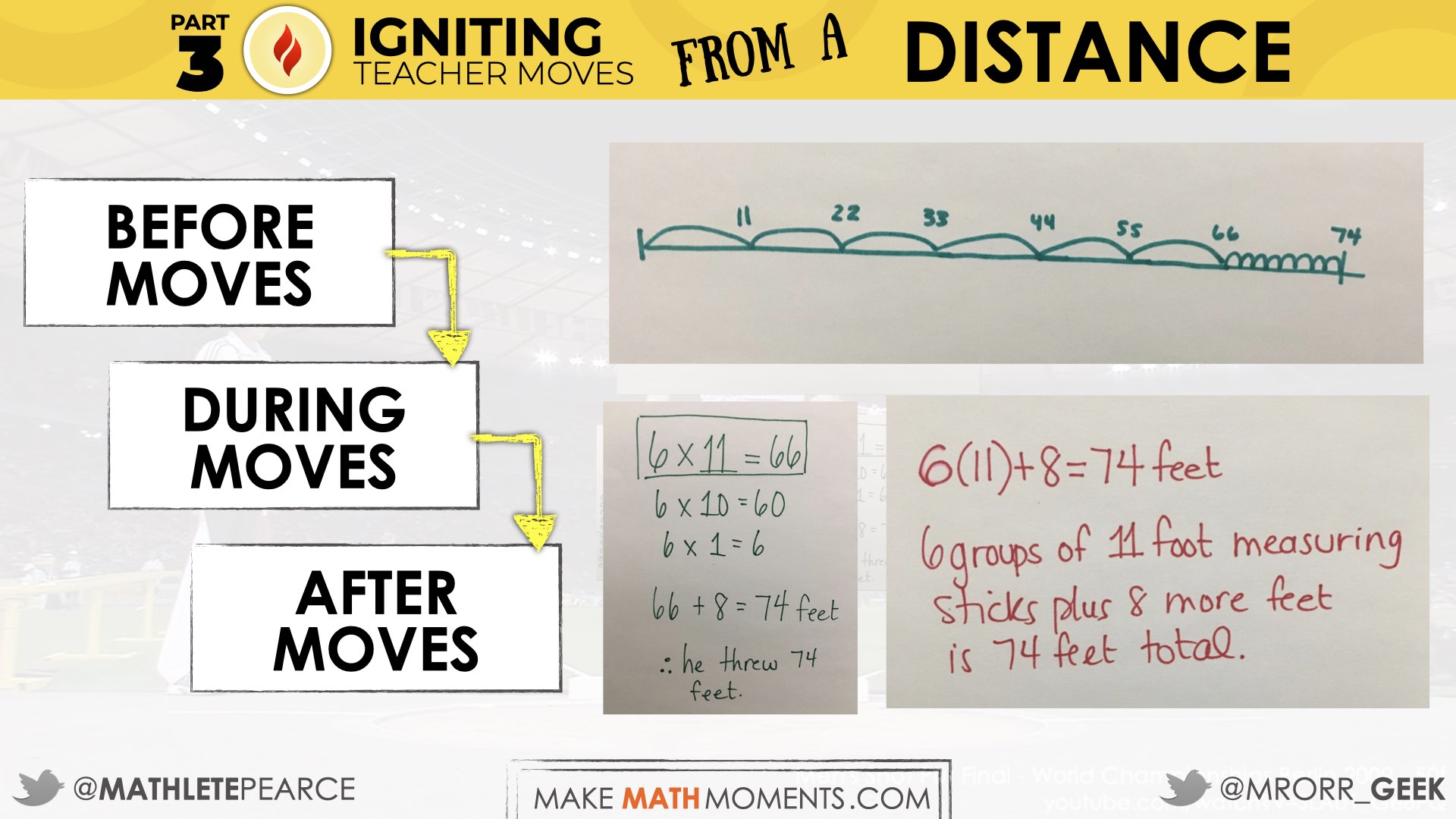
The third part of the Make Math Moments 3-Part Framework doesn’t actually happen last. It is happening before, during, and after each and every problem based lesson we teach. It’s definitely the least exciting part of the framework, but we’d argue that it is the most important.

Igniting Our “Before” Moves

For a good chunk of our teaching careers, we thought that the “before moves” for planning a math lesson was simply planning out the “note” we would write on the board and the set of  examples we’d share with students to essentially mimic by writing them down in their notebooks.

After our shift to a problem based approach to teaching mathematics, we now realize that the majority of the before moves of a lesson involve not only the planning of a task that will Spark Curiosity and Fuel Sense Making, but also anticipating what approaches students might take to solve the problem. This work requires great attention to detail and hard work, but the payoff is so rewarding and worthwhile. 

How did we have this epiphany of the importance of the teacher moves before, during, and after a lesson? The great work of Margaret (Peg) Smith and Mary Kay Stein and their work shared in the book 5 Practices for Orchestrating Productive Mathematical Discussions has had a huge impact on how we now view the planning and delivery of an effective problem based lesson.

Our “before moves” now consist of:

• identifying the learning objectives and big ideas we hope to bring to the forefront through the problem based lesson or unit of study;
• selecting, transforming, or creating a task that will allow us to craft a productive struggle for students; and,
• anticipating what solution approaches students might take to solve the task.

In Day 1 of the Shot Put unit, you’ll notice in the Teacher Guide section that we have set the learning objectives and big ideas with intentionality and as much clarity as possible. In one sentence, the purpose of the unit is to: 

• encourage students to explore solving equations using the idea of equivalence and substitution.

We also try to break that down into smaller moving parts or Big Ideas:

In this task, students will have an opportunity to reason through an investigation sparked by an athlete throwing shot put. The tasks involve the evaluation of an equation through substitution and the solving of 2-step linear equations. Students will have the opportunity to apply models to reason; in particular, making use of the double number line.

 

They will also explore big ideas including the following:

• Problems that require multiple calculations can be represented in a single equation
• Each side of an equation can be thought of as a single unit, where both sides are equivalent
• Changing the quantity on one side of an equation forces an equivalent change in the other.

Now that we – as the facilitator of the problem based lesson – are clear on the intentionality of the lesson for the day and for the remainder of the unit, we can then begin focusing on the student approaches we might see when students are productively struggling. When we think about these approaches, we are thinking through the various strategies and mathematical models that may emerge while paying special attention to the wide range of mathematical readiness that the students bring with them into our classroom each day.

Igniting Our “During” Moves

After we anticipate the various strategies and models that may emerge as students tackle this task, we also consider how we might monitor, select and sequence these approaches as they arise during the lesson. While we are thinking ahead before the lesson to help us prepare, these are ultimately during moves that happen “in the moment” while students are productively struggling.

We suggest monitoring student thinking by circulating around the room and listening to the mathematical discourse taking place between students in their visibly random groups. If we took enough time to work through the task and solve the problem in as many ways as we could during the anticipation stage, it’s likely that you’ll see many of the student solution approaches or similarities to what you may have come up with. As Peg Smith shared with us on Episode 33 of the podcast, spending a considerable amount of time anticipating student solution approaches ahead of time will reduce the amount of “thinking on the fly” that you would have to do had you not spent a considerable amount of time working through the problem. 

As students are productively struggling and we are monitoring by circulating around the room, we can then begin selecting and sequencing some of the student solution strategies and models that would be helpful for us as we plan to consolidate the lesson. 

Some common strategies for selecting and sequencing student solution approaches include:

• most accessible to least accessible solution strategies and representations;
• most common/frequent to least common/frequent strategies and representations; or,
• choose another approach to selecting and sequencing student work.

In this particular lesson, the tools and representations you might see students using to convince their peers and/or the teacher include:

• Bar models.
• Number lines.
• Symbolic representation (i.e.: 6 x 11 + 8 = 11 + 11 + 11 + 11 + 11 + 11 + 8 = 66 + 8 = 74 feet).
• And possibly others.

Some additional “during moves” we want to consider is planning and practicing the purposeful questions we can prepare for students to encourage them to share their strategies and their reasoning for how they are determining the total number of feet to measure the distance. While crafting specific purposeful questions ahead of time for posing as students productively struggle, some more generic questions that are helpful during any lesson include asking students to convince you (the teacher) and their peers that their answer is correct by sharing their mathematical models. If their approach is too abstract or incomplete, then they will have trouble convincing our math community and thus they’ll need to add to their body of work by adding more detail to their current representation or introduce one or more additional models to build their case.

Igniting Our “After” Moves

After we’ve monitored, selected, and sequenced the student approaches we plan to use as a jumping off point for making connections with our students, we now begin thinking about our after moves of the lesson. While some might think that “after moves” would be taking place after the class ends and students have filed out of the room, what we’re referring to are the moves that take place after the productive struggle of the lesson. These after moves are how we go about discussing the student solution approaches that we had selected and sequenced for use during the consolidation phase of the lesson.

As we begin the consolidation, we will discuss the strategies shared and elicit student thinking to build off of their current prior knowledge and understanding rather than “fixing” or “funnelling” student thinking to a strategy and/or model that does not connect to their strategy and/or approach.

With this first provocation we used to Spark Curiosity and Fuel Sense Making, students were given an opportunity to use algebraic thinking where they knew:

6 iterations of the brown measuring stick plus 8 additional feet is equivalent to the length of the shot put throw.

Symbolically, this can be written as:

6b + 8 = l

where b represents the length of each measuring stick (or rate) and l represents the total length of the shot put throw.

Using student generated solution approaches and strategies to facilitate a discussion intended to connect student approaches which may involve separate calculations into a single equation. 

For example, in Student Approach #2, the student first multiplied 6 sticks x 11 feet per stick using partial products to reveal a total of 66 feet. Then, the student added the additional 8 feet in a separate step and/or equation:

6 x 11 = 6 x 10 + 6 x 1 = 60 + 6 = 66

66 + 8 = 74

Help students see how this approach can be represented in a single equation.

6 x 11 + 8 = 74

or

6(11) + 8 = 74

This is an important step in nudging students towards constructing an understanding of equations involving unknown values.

For example, in this particular problem, we were working with this equation:

6x + 8 = l 

where x represents the length of each measuring stick and l represents the length of the shot put throw. 

Since we are then given x = 11 feet, students can substitute 11 feet for x:

6(11 feet) + 8 feet = l

66 feet + 8 feet = l

74 feet = l

You might find the following animation and visual helpful as you prepare for this consolidation or even potentially use during the consolidation:

After connections are made during consolidation using student generated solution approaches, we can then “reveal” what really happened if at all possible.

From here, we then use what we know about our learners based on what we observed during the productive struggle and throughout the consolidation of the lesson. The big question we are trying to answer is whether it appears that students are ready for us to proceed as planned by moving on to the next part of our lesson and/or unit or should we be pivoting our plan to address any gaps or misconceptions that still exist. 

If a significant portion of the group could use more experience with this idea of substitution, then we might consider having them work on a consolidation prompt giving another throw and sharing a different length measuring stick for them to use. For example, asking students to determine how far another shot put was thrown that required iterating an orange measuring stick 5 times plus an additional 2 feet paced out by the official.

Proceeding As Planned With An Extension

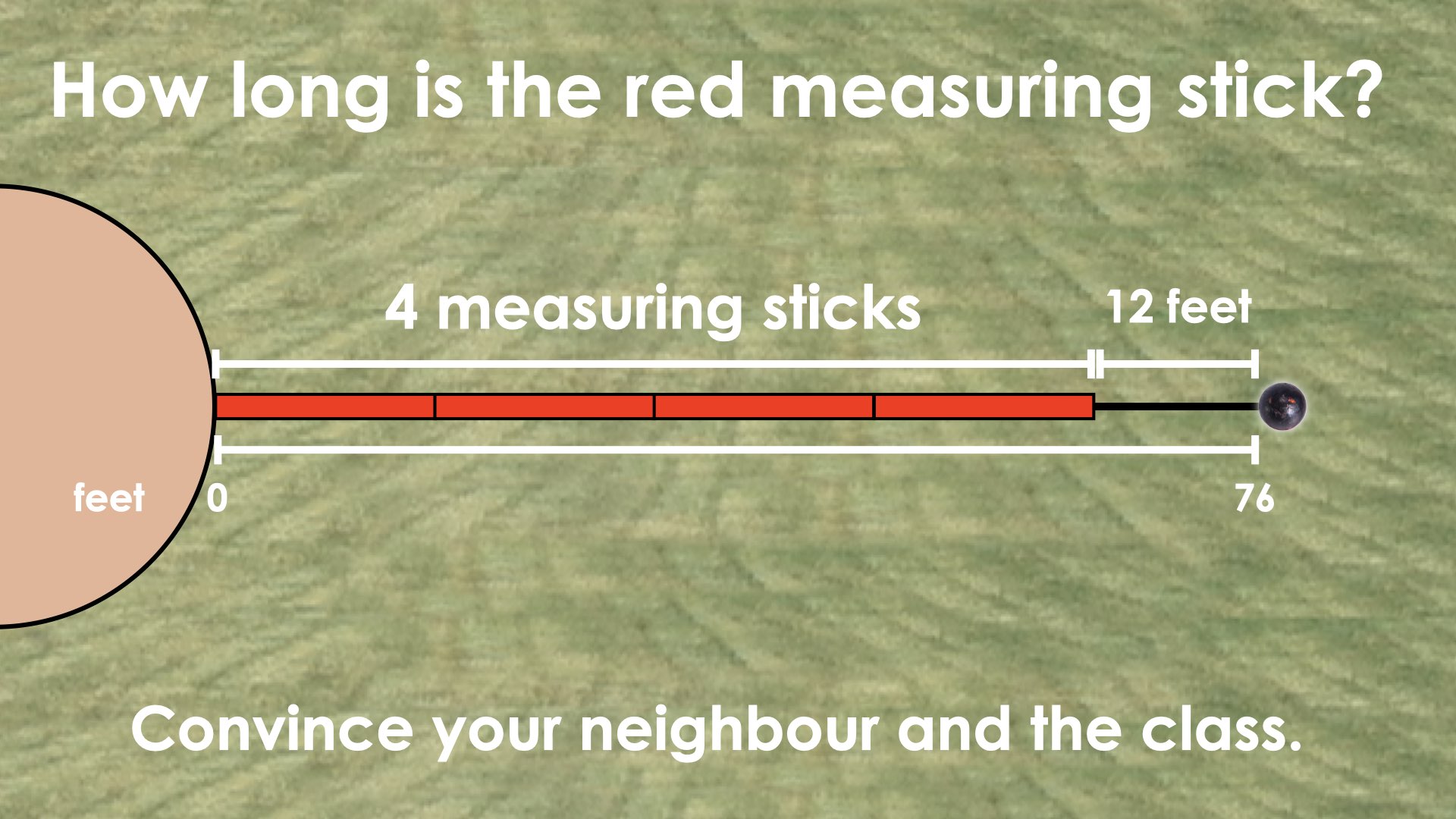
If only a handful of students require some additional attention in this area, we can document their names and be sure to follow-up with them by creating time for small group instruction while proceeding as planned by setting up the remainder of the group to by working on an extension problem to extend this idea to solving two-step linear equations like the following:

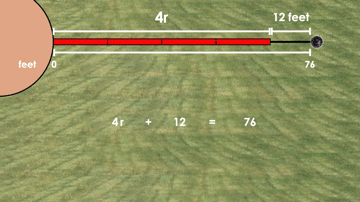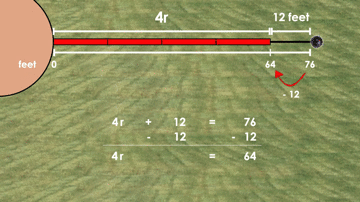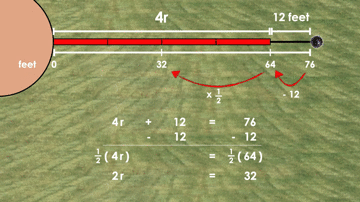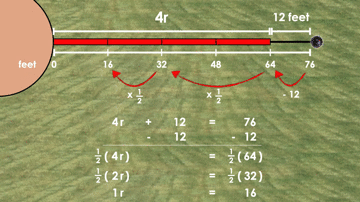
On the second throw, the shot put landed at the 76 foot marker. The officials used 4 measuring sticks and had to pace out 12 extra feet to measure the total distance. 

How long were the measuring sticks?

You’ll notice that with this extension, we are riding the “curiosity coattails” of the original shot put prompt and essentially getting a fastpass to enter into another round of Fuelling Sense Making and Igniting Our Teacher Moves. 

While we won’t get into it too deeply here, my favourite part of Day 1 of the Shot Put Problem Based Unit is the different student solution strategies that emerge from this prompt. One of the big ideas we hope to highlight through this particular prompt is the idea of “undoing” by subtracting the additional 12 feet and then scaling down both the number of sticks and the total distance. 

For example, some students leverage a halving strategy to help them arrive at the rate of feet per stick and this can be connected to the symbolic representation using and solving an algebraic equation using the same strategy:

Very cool and lots of amazing learning to be had here.

Setting Conditions To Ignite Teacher Moves From A Distance

So we’ve taken some time to discuss some of the key elements of the teacher moves we want to ignite before, during and after a lesson, so let’s take a moment to unpack how we can set those conditions to ensure this is possible from a distance both synchronously and/or asynchronously.

Some of the key before moves we want to ensure that we are implementing include anticipating student approaches, strategies, and mathematical models. However, this is really challenging work if we don’t know and understand where each student in our classroom is coming from both as an individual and where they are along the mathematical trajectory.

While the during moves of monitoring, selecting, and sequencing borrowed from the 5 Practices for Orchestrating Productive Mathematical Discussions will take a lot of practice to become both familiar and comfortable with implementing during each problem based lesson, one of the conditions we must set as students are productively struggling is staying curious to avoid robbing students of their own thinking. One of the ways that we try to do this is by reflecting on a quote by Michael Bungay Stanier in his book, The Coaching Habit where he asks the reader:

Can you stay curious a little bit longer, and can you rush to action and advice giving just a little bit more slowly? 

~ Michael Bungay Stanier, The Coaching Habit

At the core of the Make Math Moments 3-Part Framework is the idea of curiosity – not only for getting students to lean in during lessons, but also to ensure that we do not force our thinking on students.

Finally, setting the conditions to ensure that we effectively implement the after moves requires pre-planning what our intentionality for our lesson is and what big ideas we hope to emerge. Which student solution approaches might we see and how can we leverage their strategies and mathematical models to highlight the intended learning explicitly so all students are able to leave this mathematical experience with something new to take away. As we plan the before, during, and after moves of each problem based lesson, what does proceeding as planned look like? What might a pivot to our plan look like? 

Having a comfort with all three phases of Igniting Teacher Moves is important to ensure that we lead a problem based lesson that flies instead of flops.

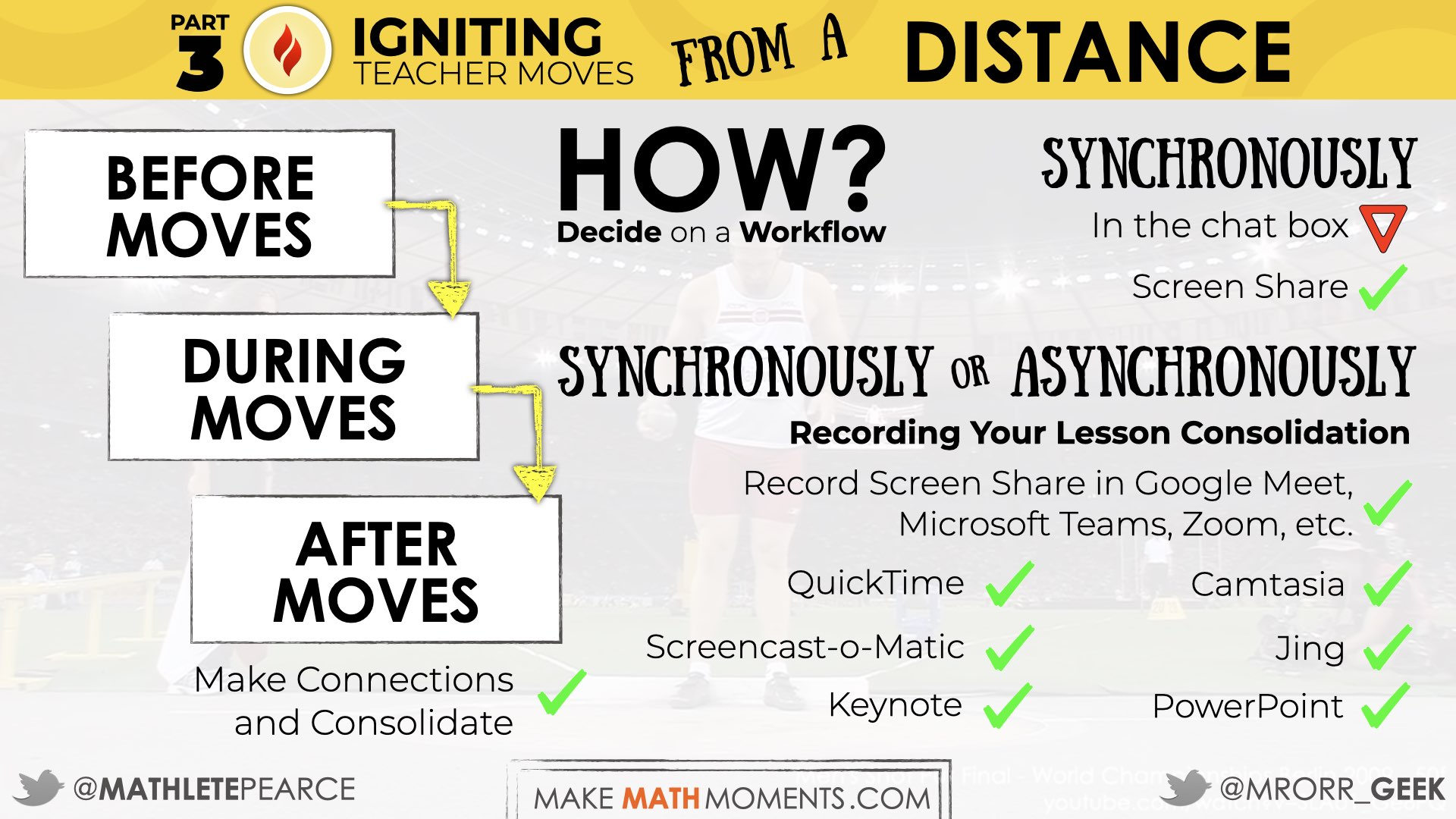
Tech Tools to Ignite Teacher Moves Synchronously and Asynchronously

If learning and implementing how to Ignite Teacher Moves isn’t already complex enough in a face-to-face learning environment, trying to hone in on the before, during, and after moves of a Make Math Moments problem based lesson while teaching remotely in an online environment adds another layer of complexity. 

It seems more and more districts are pushing educators to teach synchronous lessons with their students, so in that case, leveraging some of the tools shared earlier like Knowledgehook SnapShots, Flipgrid, Padlet, or even using Desmos Activity Builder can be helpful to Ignite Your Teacher Moves. Another feature that might not seem obvious, but is extremely useful is the screen share feature that most web conferencing tools like Zoom, Google Meet, Microsoft Teams and many others have built in to their platform.

Despite how helpful many of the tools we’ve shared throughout this post can be to improve the effectiveness of delivering a Make Math Moments problem based lesson in an online remote learning environment, trying to monitor, select, and sequence during your synchronous lesson can be challenging with a large group of students. In particular, trying to glean the same formative assessment data you could collect via observations and conversations in a face-to-face environment is difficult with all of your students lumped into one big digital group. Thankfully, some of the most commonly used web conferencing tools have built-in features or “hacks” that can be used to create smaller, more manageable groups. 

For example, Zoom has the ability to split up your meeting into up to 50 different “breakout rooms”, while it appears that there is a “hack” to do the same in Microsoft Teams (here’s a video) and in Google Meet.

If you’re doing some (or all) of your teaching asynchronously, then consider planning and recording the consolidation of your lesson after students have submitted their thinking via the tools of your choice shared previously and leverage the screen share feature in your web conferencing software to easily capture a short video to help explicitly make connections to your learning objectives and the big ideas from your lesson.

Recording your lesson consolidation using a web conferencing tool is not your only option. Here is a pretty well-rounded list of tools that can help you record your consolidation for sharing with students asynchronously.

Tech Tools To Record Your Consolidation

• Record With Web Conferencing Software (Google Meet, Microsoft Teams, Zoom, etc.)
• QuickTime (MacOS only)
• Camtasia
• Screencast-o-Matic
• Jing
• Loom
• Keynote
• PowerPoint 
• …and many more

You may be wondering why I ended the list with Apple Keynote and Microsoft PowerPoint, two slideshow presentation tools. Well, despite how common these two tools are for building out lessons, many people do not realize that they both have a screen record feature built right into the software. This means any of your slide decks that you’ve built out in the past can easily be used to record your lesson with a voiceover. That is how we here at Make Math Moments record our lesson consolidations (using Apple Keynote) and we find the experience to be quite smooth.

How Did We Do?

Wow, that was a lot to take in and we’re so proud of you for making it to this point. 

As we mentioned earlier in this article, there is no combination of tech tools out there that can ever replace the effectiveness and connectedness of learning mathematics in a face-to-face environment. However, we certainly do hope that the information shared in this post has provided you with some help trying to both implement a problem based math lesson using the Make Math Moments 3-Part Framework and setting the conditions where you can effectively deliver those lessons in an online remote learning environment consistently and with confidence. 

In particular, we intended to summarize some of the key learning objectives we shared for those who participated in our Make Math Moments From A Distance webinars recently including:

• How to deliver problem based lessons in a meaningful way;
• How to reach all students regardless of their mathematical readiness through the use of emerging mathematical strategies and models; and, 
• How to deliver engaging lessons over the internet synchronously or asynchronously.

So now it is your turn. 

Did we deliver on those key learning objectives? 

Let us know in the comments!

Are you looking to dive even deeper by taking our full Make Math Moments From A Distance course?

You can by joining the Make Math Moments Academy. 

Best of all, your first 30 days are on us and you can cancel your membership anytime.

Join the Academy now.

DID YOU GRAB THE CHEAT SHEETS?

HAVE YOU DOWNLOADED THE 3-PART GUIDEBOOK?

LEAVE A COMMENT: