Have you been curious about spiralling your math curriculum? Heard colleagues talking about it, but not quite sure what it is, what the benefits are and how you can get started in your own classroom? Then this post is for you!

For the last 5 years or so, I have been experimenting with different ways to spiral my math courses and a recent discussion on Twitter sparked by Jon Orr had me search back to a draft blog post I had been working on, but had left incomplete.

Here’s what Jon had asked the Twitterverse:

With over 20 people throwing out great things to consider, I thought it would be worthwhile to share some strategies to help you get started spiralling in your math classroom.

Before we begin, we should probably clarify what a spiralled math curriculum actually is.

What Is Spiralling the Math Curriculum?

When we spiral curriculum in math class, we are organizing topics that might traditionally be taught in blocks, chapters, or units of study over a short period of time and we are introducing topics in smaller chunks and spreading them out over a longer period of time. While you can do this in many different ways, it is common to come back to the topic multiple times over the duration of the grade or course and going deeper each time. Spiralling is commonly referred to as “interleaving”, “distributing”, “spacing” or “mixing” the topics from the math curriculum, while teaching a concept in one unit or chapter like you see in many textbooks is commonly referred to as “blocked” or “massed” approaches.

Generally when I think of spiralling math curriculum, I picture spiralling through all of the big ideas through tasks early on in the course at a surface level. At the end of this first spiral, we go back through these same ideas to build on our surface knowledge and dig deeper. We continue to spiral through these concepts introducing more complex and rigorous tasks as we help students build their conceptual understanding and develop procedural fluency. I like to see this thinking as very similar to that of John Hattie when he speaks about surface learning and deep learning. By spiralling the curriculum and using well planned, thoughtful guided inquiries and investigations, you can help students develop much needed surface learning and deep learning.

When you read about this spiralling, the big question many may have is “why can’t I do this by organizing my curriculum in units like I always have?” Well, the research suggests that loading up all of the learning for a concept over a continuous block of time just doesn’t have the same effect as mixing it up and spreading it out.

Why Interleaving Is Better Than Blocking

When we interleave math concepts throughout the duration of a course rather than approaching that concept in a continuous block over a shorter period of time, research from over the past 100 years suggests that students learn concepts more deeply and they retain that information for a longer period of time versus blocking.

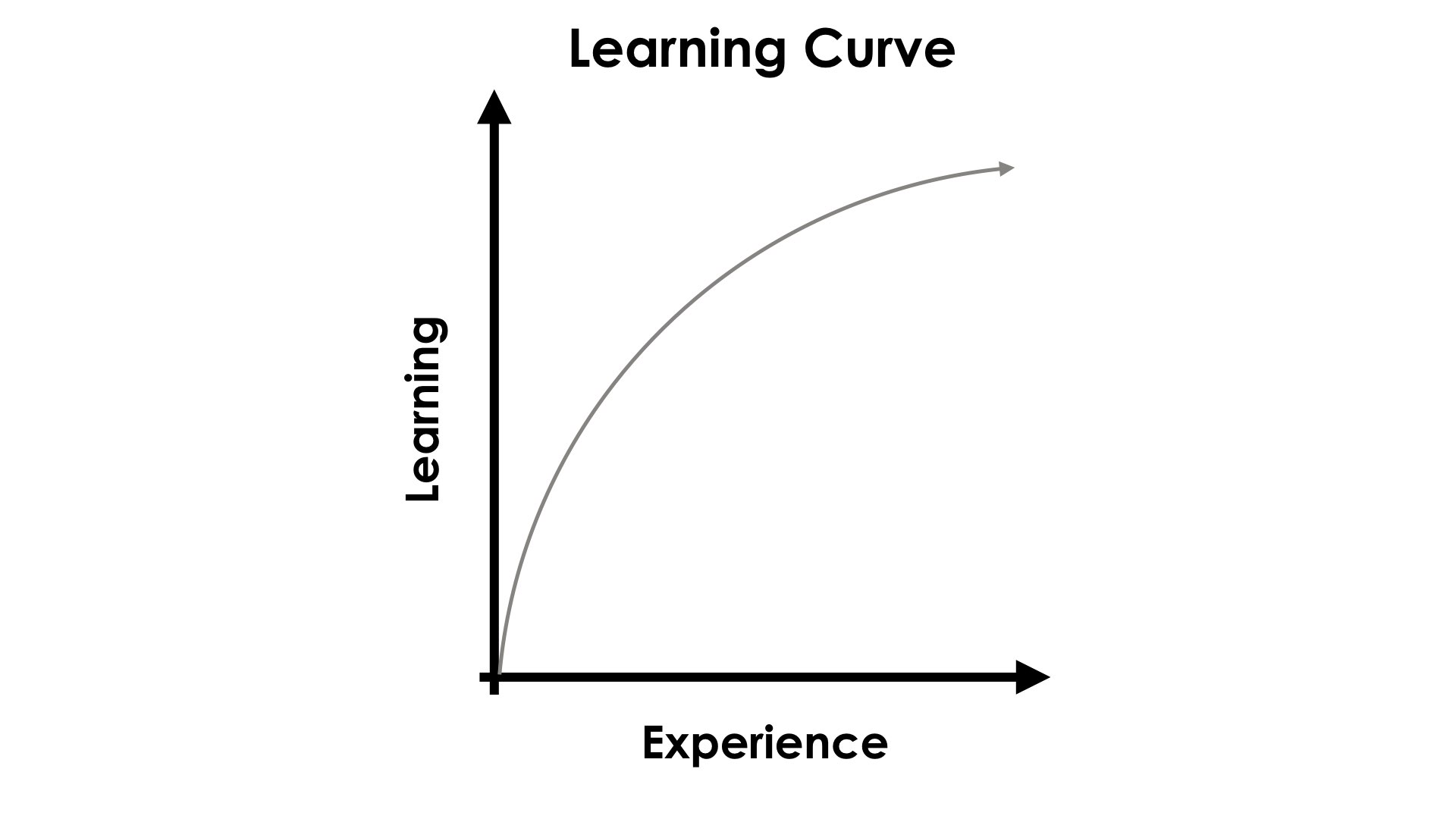
Hermann Ebbinghaus & The Learning Curve

Experiments by Herman Ebbinghaus which were conducted on himself were the first to investigate properties of human memory. In his experiments, Ebbinghaus would create a lists of about 20 three letter words. These nonsensical words were created starting with a constant, followed by a vowel, and ending with a constant.

To test the process of committing new learning to memory, he would read and say each item on the list, before moving onto the next. When he was finished the entire list, he would return to the beginning of the list and repeat the process. As you would expect, as the repetitions increased, so did his ability to recall the items in the list. This work by Ebbinghaus was responsible for the creation of the world’s first learning curve.

The Forgetting Curve

While these experiments were exciting, what Ebbinghaus is most well known for is the forgetting curve. Using the same types of 3 letter, nonsensical lists of syllables, he then began focusing his experiments on how long he could retain these items in his memory over time. His research showed that once he had “learned” a list, his retention would decrease with each passing day that he did not attempt retrieving the items from his memory. However, when he retrieved a list from his memory after short intervals of time that gradually increased, the forgetting curve would become less steep.

In the graph below, we can see an example retrieving information from memory after 1, 3 and 6 days after initial learning:

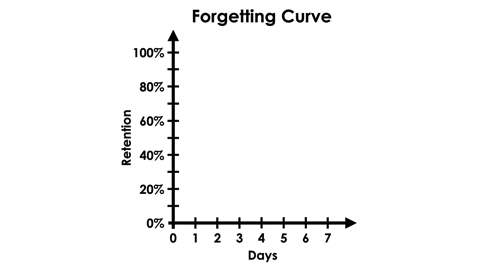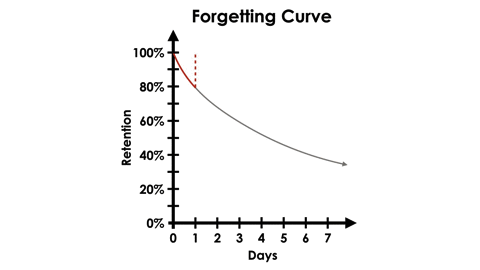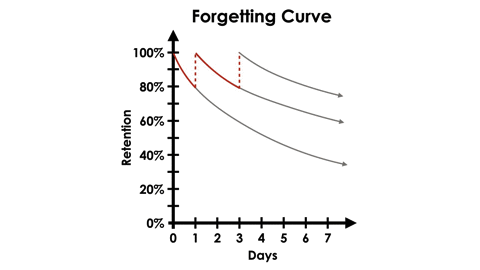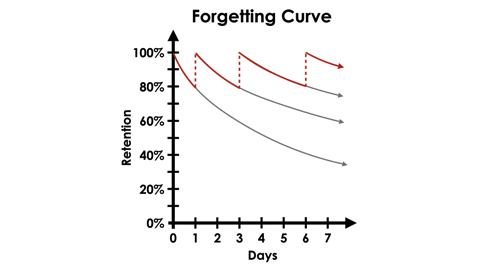
Ebbinghaus believed that the speed of forgetting depends on a number of factors such as the difficulty of the learned material (in other words, how meaningful it is to the individual), its representation (such as what connections to prior learning is made with the new learning) and and physiological factors such as stress, sleep or even how open to learning the individual is.

Other Research Supporting Spacing Over Massing

In The Educational Psychology Review, Son and Simon state:

“On the whole, both in the laboratory and the classroom, both in adults and in children, and in the cognitive and motor learning domains, spacing leads to better performance than massing.”

Son, L. K., & Simon, D. A. Distributed learning: Data, metacognition, and educational implications. Educational Psychology Review (2012): 1-21.

Surprisingly, much of what we believe to be true about learning is actually false as explained in Benedict Carey’s book How We Learn: The Surprising Truth About When, Where, and Why it Happens:

Let go of what you feel you should be doing, all that repetitive, over-scheduled, driven, focused ritual. Let go, and watch how the presumed enemies of learning – ignorance, distraction, interruption, restlessness, even quitting – can work in your favor.

Carey, Benedict. 2014. How we learn: the surprising truth about when, where, and why it happens (222)

Seems pretty counterintuitive, but interesting none the less.

Wonder and Curiosity Drives Learning

While I won’t be suggesting that we promote distractions, interruptions, restlessness and quitting in our math classes, some of the key ideas from the book have interesting implications for math class and school in general. First and foremost, Carey concludes that learning happens best when it is driven by wonder and curiosity rather than by fear or envy. When you consider the traditional approach to teaching math class is usually blocking or massing concepts in a short period of time followed by a one shot test, it would seem that the learning is more likely to be driven by fear (i.e.: failing) or envy (i.e.: wanting the highest grade) rather than by wonder and curiosity as Carey suggests.

In order to promote learning driven by wonder and curiosity, Carey argues that we should help students become curious thinkers – not as a means to do individual tasks like completing a section in a textbook, but for cultivating a love of learning in general. As a teacher who used to teach in units or blocks, I find it much easier to spark curiosity in my students when I spiral math curriculum using 3 act math tasks to teach concepts because solution strategies are much less predictable, students are not expected to use a specific formula or algorithm explicitly taught moments before during a teacher directed lesson and each of these contextual tasks creates an intellectual need for the learning.

I know that if I can get students curious about a problem and get them to put some skin in the game by sharing what they notice and wonder as well as making predictions before all of the required information is shared, students are much more likely to learn and retain this new knowledge.

Effect of Spiralling on Retention

Although the decades of research has clearly indicated that interleaving math concepts and spacing practice is much more effective than teaching in blocks and massing practice, we are still seeing the majority of textbooks and math classes organized in units or blocks.

Why?

One possible reason is because of the illusion of understanding often experienced when we teach or learn using blocked instruction and massed practice. Because students are focusing their attention on few concepts and practicing them repeatedly over a short period of time, the facts, steps and procedures are fresh in their minds and they appear to “know it”. Unfortunately, this perceived fluency is short lived and often results in a lack of retention over time. Many of us and our students have experienced this sort of memory loss when we “draw a blank” on a written assessment and I’m sure every teacher has had their students claim they don’t remember how to solve a problem related to a concept they learned the previous year.

When we distribute or interleave concepts and space practice over time, this forces our brains to work harder to retrieve the information and ultimately builds our retrieval strength. By waiting to come back to a concept just before it feels like it is fully forgotten, we are giving our brains exercise to retrieve those memories and build a stronger neural pathway to that information. Thus, Carey not only recommends interleaving and spacing practice, but also using tests as an effective studying technique to promote retention rather than just as a measurement tool. The logic here is that each test where a student works on problems independently and without the aide of peers or resources is an opportunity for them to practice retrieving that information that is stored deep in their brain.

Imagine that: using a test to study rather than studying for the test.

I like it!

Some Jurisdictions Explicitly Promote a Spiralled Curriculum

Interestingly enough, my colleague Jana LePage-Kljajic brought to my attention the fact that the Ontario Mathematics Curriculum explicitly states that teachers should be teaching in some sort of spiralled format:

“When developing their mathematics program and units of study from this document, teachers are expected to weave together related expectations from different strands, as well as the relevant process expectations, in order to create an overall program that integrates and balances concept development, skill acquisition, the use of processes, and applications.”

The Ontario Curriculum Grades 1 – 8 Mathematics 2005, page 7

Recently, the Ontario Ministry of Education released a completely spiralled Grade 1 to Grade 8 Math Resource on the EduGains website called TIPS4Math. Definitely a great place to start if you are teaching elementary mathematics in Ontario.

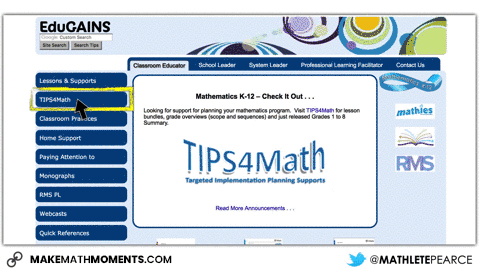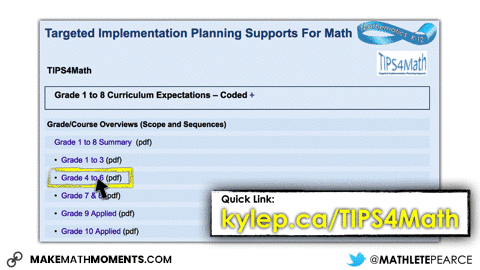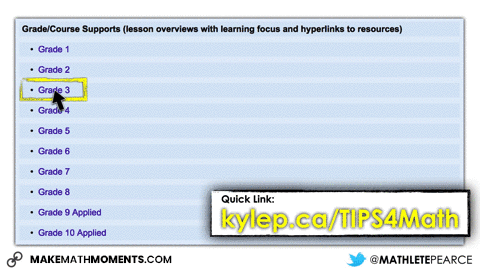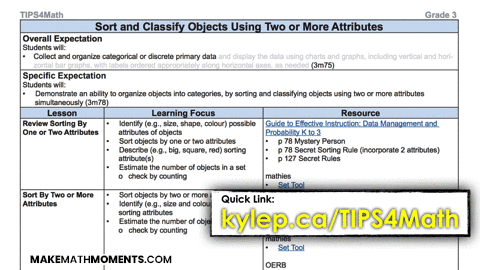
Although I couldn’t find it stated as explicitly, the Common Core State Standards (CCSS) for Mathematics does mention a spiral-like approach:

… not only stressing conceptual understanding of key ideas, but also by continually returning to organizing principles such as place value and the laws of arithmetic to structure those ideas.

Common Core State Standards (CCSS) for Mathematics

Although I’m less familiar with the University of Chicago’s Everyday Math program, it is also a spiralled curriculum and they share their logic behind the organization here.

Part 2: 6 Steps to Spiralling Your Math Class Now

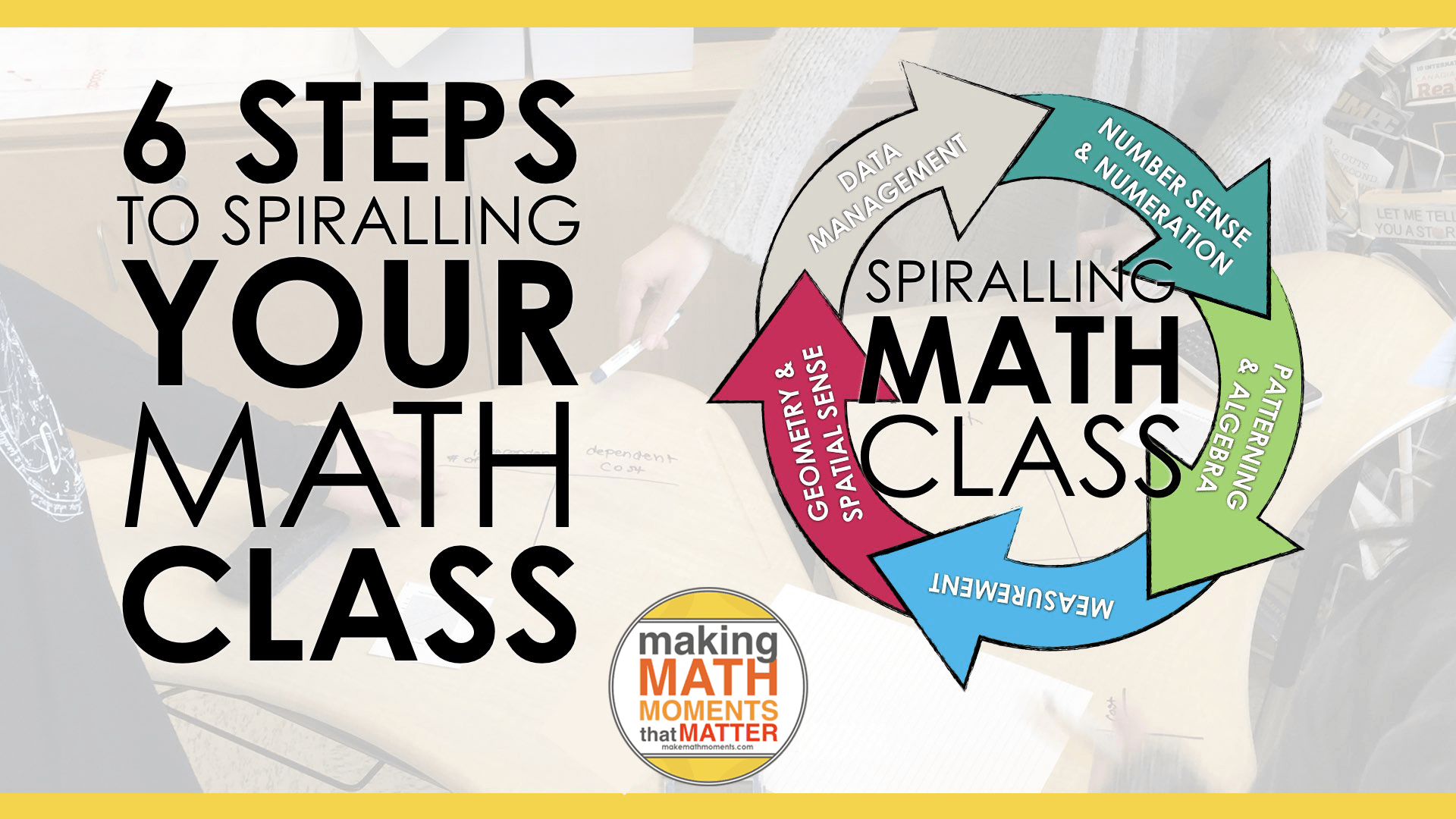
Since you’ve made it this far in the post, that likely means that you’re interested in exploring this approach further and getting started. Awesome!

While many teachers have very different perspectives when it comes to getting started – from dipping your toes to diving in head first – I’d like to propose some steps that will help guide you along the way.

Spiralling Step #1 – Know What You Need To Teach

In other words, know your curriculum. If you are brand new to teaching a grade or course, trying to spiral for the first time will be challenging. That said, I’m not suggesting you don’t attempt spiralling, but rather be aware that you will have to do some serious digging into the expectations or standards you will be teaching in order to plan and deliver your spiralled curriculum with confidence.

In reality, the work you need to do upfront to learn the curriculum should be done by every teacher regardless of how you intend to structure your long range plan. Unfortunately, teaching math in blocked units as they are in most textbooks can unintentionally make it possible for us to learn new curriculum one unit at a time. When faced with teaching a new grade or new courses, sometimes we can feel so overwhelmed that we tend to plan our year in small blocks or chunks which is not ideal for student learning.

Spiralling Step #2 – Assess By Learning Goal or Standards Based Grading

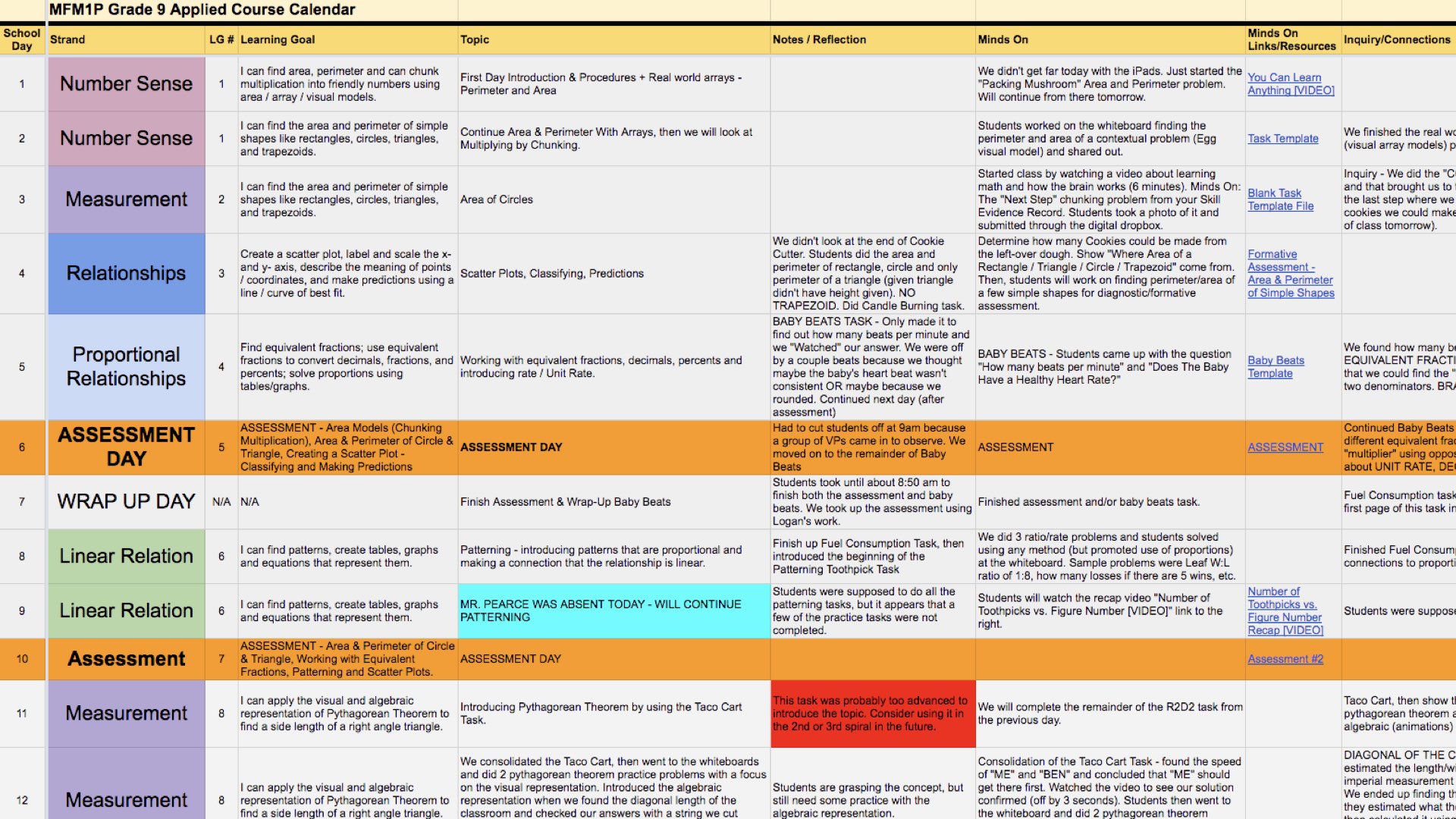
When I attempted spiralling my MFM1P Grade 9 Applied math course for the first time, it was after I had been assessing students by learning goal and success criteria or as some in the united states might call it: standards based grading (SBG). I personally believe that by assessing in this manner, it forced me to really know and understand the curriculum I was teaching. Not only does this step serve as a way to ensure that you can check step #1 off the list, but this has other benefits for your classroom beyond the spiralling of concepts. Assessing by learning goal is a great way to help identify where students are strong and where they need more support so you can offer specific and timely feedback.

By monitoring how students are doing based on the learning goals you have created for your course, this can also help you determine how frequently to come back to concepts based on student understanding. In contrast, assessing a mark on a unit test alone is much less helpful when it comes to trying to determine what concepts we need to spiral back to and can often lead us to attempting to re-teach the entire unit – wasting valuable class time – rather than focusing on the specific topics where students are struggling.

LEARN MORE

Spiralling Step #3 – Create Topics, Strands or Big Ideas

I don’t care what you call them. Some might like calling them “topics” or “big ideas”, while others might have their own creative name for them. Regardless of what you want to call them, you definitely want to look at your curriculum, the learning goals you’ve created and start organizing them. The Ontario Curriculum conveniently organizes our expectations into strands, so that is where I began my first time through spiralling grade 9 applied. I also decided to keep the name “strands” although I had subdivided them into smaller groups.

Now that might sound confusing, especially if you’re not from Ontario like I am, so let’s have a close look.

Here’s a glimpse of the Grade 9 Applied Spiralled Course Google Sheet I was using to organize my course, which I will share in the resources under this video. Luckily for me, Jon Orr was also interested in trying to spiral his grade 9 applied course at the same time which made the process so much easier.

While we were collaborating and helping each other think through how we might teach our courses, we would often go in a different order based on our own student learning needs, but we would often times be using many of the same tasks and lessons.

ACCESS THE GOOGLE SHEET

On the other hand, maybe you prefer planning with physical paper like my colleague Jana LePage-Kljajic who prints out the curriculum and cuts them up into individual expectations. Then, after grouping them, she glues them to colour paper to help her see the big picture.

Regardless of how you want to do it, I’d recommend coming up with a plan to organize your topics in a way you think would be easiest for your own personal organizational style.

Spiralling Step #4 – Plan Your Cycles, Spirals or Chunks

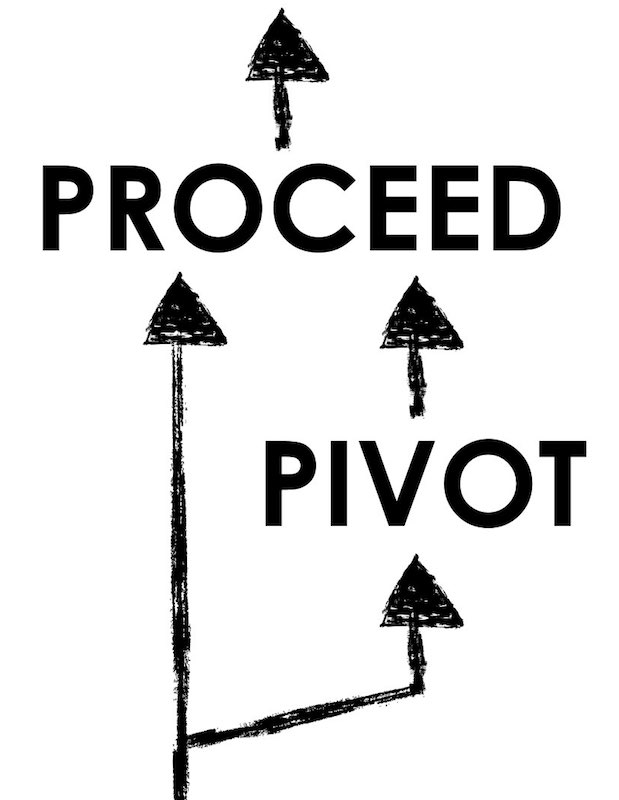
Spiralling Step #5 – Be Comfortable With Changing Your Plan

Spiralling Step #6 – Interleave Your Assessments

We are all assessing students through conversations and observations on a daily basis. However, if you’re spiralling your course, it might seem hard to determine when you will assess students with a written test or quiz and what questions you should be asking.

Since we are spiralling the content of the course, it would make sense that the assessments are spiralled or interleaved as well. For me, I would give students an assessment on “Mastery Day” which was every Tuesday and the assessment was called a “check-in”. For the first half of class, students would work on 4 to 6 questions; approximately half from ideas we worked with the previous week and the other half would be from anything covered previously in the course. The intention here was to give me and the student a true understanding of where their understanding was related to those learning goals at the current time. There was no review day and there was no list of concepts they were to cram the night before. Just questions to give students the opportunity to strengthen their retrieval strength and highlight areas that they should be focusing on over the next week.

After submitting their check-in, the second half of the class would be used to work towards mastering a concept based on the feedback given on previous check-ins. Here’s a post explaining how I shared that feedback, but save that reading for later as it will send you down a whole new rabbit hole for exploring separately.

I would try my best to have feedback for students done by the next day not only for the feedback to be timely for them, but also to help me determine whether I should continue the next week of my spiral as planned or whether I need to come back to an idea like Pythagorean Theorem because so many students crashed hard on it. There are also some positives that come from this like realizing that my students really understand linear relations and maybe I can cut a day out of this spiral to commit to something else.

Now, although I have interleaving your assessments as the 6th step, I’ll mention that you might also consider doing this step after step 3, if you feel that you aren’t ready to spiral your lessons, but could see yourself interleaving the content on each assessment. This is also a step that may be easier to put into practice during a school year, whereas spiralling the content in your lessons could be thought of as more challenging if you’ve already begun teaching in blocks or units.

Whew! That’s a lot to consider if you want to dive straight into spiralling your math curriculum.

If that seems overwhelming, then maybe you might want to consider just easing into the idea of spiralling, interleaving, spacing and mixing portions of your math class.

Well, you’re in luck! In the next couple of days, I’ll be sharing 9 Spiralling Starter Strategies to Begin NOW!

Part 3: 9 Steps to Spiralling Your Math Class NOW!

Spiralling is a pretty complex way to organize your course, but with positive implications for student learning. If you’re feeling a bit scared, stressed, or anxious, that’s O.K.! I am certain that with all of the ideas I’ll be sharing with you in this video, you will be able to find a method that will help you get started based on your current comfort level.

Although I shared 6 steps to start spiralling in your math class earlier, the reality is that you might not be feeling ready to take the plunge by spiralling the lesson content in your course. Rather than avoiding spiralling altogether, why not leverage the research around spiralling, interleaving, spaced practice and mixing by starting with one of the following easy to begin strategies.

After reading the many ideas shared by the Math Twitter Blogosphere in response to a tweet by Jon Orr, I’ve managed to summarize much of what was shared into these 9 Spiralling Starter Strategies. All of these strategies are really useful ideas that can be used as very non-threatening first steps to spiralling, so let’s dive in!

Spiralling Starter Strategy #1: Find a Buddy

There is nothing more scary than taking on a new idea alone. The best part is, you don’t have to! Reach out to colleagues in your school who might be open to trying something new and work out a plan together.

Maybe you don’t agree on everything, but at least you’ll have a sounding board to share and borrow ideas from.

Mary Bourassa recognizes how big of a jump spiralling is and suggests seeking mentorship from someone who has tried spiralling in some capacity:

Can’t find someone in your building or close by to collaborate with? Mr. Hogg urges you to use online resources that are free and accessible anytime such as reading teacher blogs and connecting with other math educators on Twitter.

Jessica McConnell takes seeking out math teachers online a step further recommending that you not only connect with math teachers who teach the same grade level, but also connect with teachers who teach younger students and with those who teach older students. Then, you can make better decisions of where and when to introduce topics as well as how long to anticipate spending on those concepts.

Spiralling Starter Strategy #2: Spiralling Warm-Up Activities and/or Practice Problems

Whether you call them bell work, bell ringers, warm-ups, or mind busters, many math teachers use some form of warm-up task to begin their lesson.

Early in my career I would make the warm-up problem related directly to the previous lesson, which seemed to work nicely. But why not stretch back and warm up to a problem involving a topic we haven’t seen in a while to build that retrieval strength?

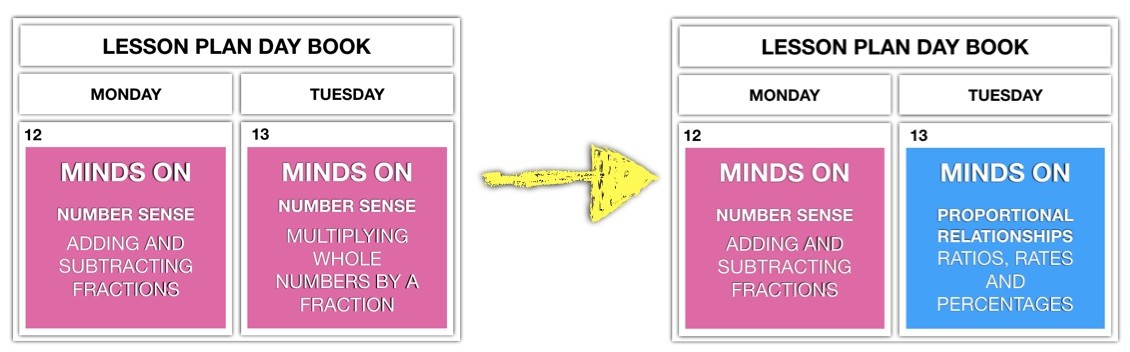
Once you’re comfortable interleaving your warm-up problems, you might consider interleaving the independent practice problems you plan to assign. Instead of assigning problems that are all related to the content we focused on today, why not assign some from today and some from the past?

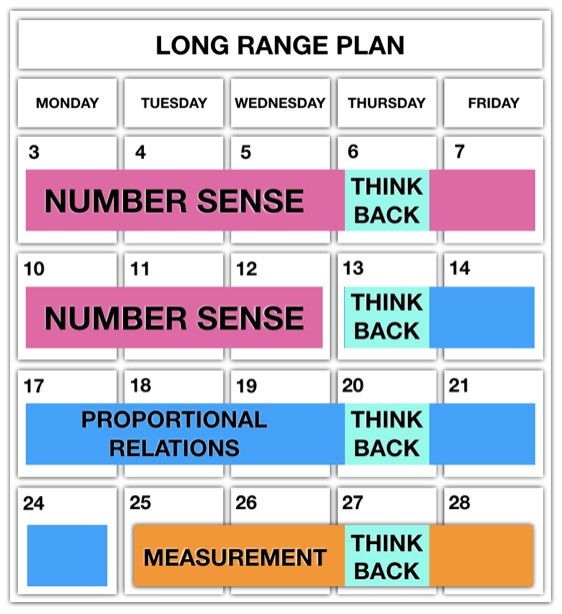
Spiralling Starter Strategy #3: Think Back Thursdays

Consider taking one day of the week to engage in your interleaving investigations. While it can be daunting to think that you are going to spiral all of your well organized and thoughtfully planned units of study, it’s definitely reasonable to think that you’ll commit one day a week to mixing things up. While I’m pretty proud to have come up with “Think Back Thursdays” as an option, the reality is that you can pick any day of the week and call it whatever you’d like!

A variation of this idea was brought to my attention by Norma Gordon when she recommended Monday Make Overs or Friday Fix-Ups where you spiral back to concepts students are struggling on for a re-attempt at learning.

Spiralling Starter Strategy #4: Interleave Your Assessments

When I was teaching in units or blocks, I would typically give assessments throughout the unit and at the end of the unit. Consider giving assessments at the same point you would during your current unit of study, but give an assortment of problems related to the current unit and some from previous units. While I think this is a great way to slowly introduce the concepts of spiralling in your math class, I think using this strategy would be most beneficial if introduced by a teacher who is progressive in the area of assessment.

What I mean by this is that the assessments we are giving our students are actually being used as a way to push the learning further rather than simply labelling a student with a letter. While this strategy is easy to implement on paper, I feel that it would be more of a punishment for students if the teacher using the strategy does not believe in giving students multiple opportunities to learn and demonstrate that learning.

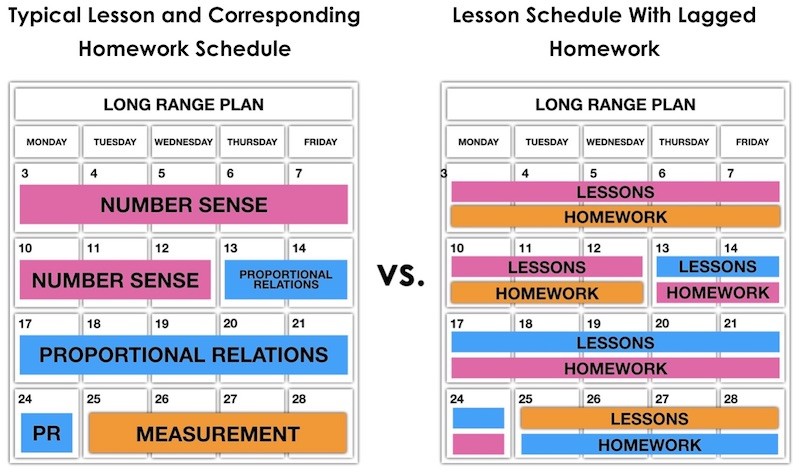
Spiralling Starter Strategy #5: Lag Your Homework

If you are teaching a math course where homework is developmentally appropriate – say Grade 7 or so and up – Henri Picciotto suggests that you “lag” homework. Lagging homework involves having your students practicing concepts from the past – say topics from last week – instead of working on a brand new concept introduced that day. The logic here is that students are given some time to digest the new ideas and are not left all alone at home with an unfamiliar concept to work on.

Spiralling Starter Strategy #6: Look For Multiple Connections in Your Tasks

It is highly likely that you are already using some really rich tasks throughout your course. Both Ve Anusic and Heather Theijsmeijer suggest we can easily start by spending more time on intentionally noticing how the tasks you are already using connect to other topics.

By looking at tasks through the lens of different big ideas or strands in your course, you will have an easier time making multiple topic connections while still feeling as though you’re organizing your curriculum in blocks.

Spiralling Starter Strategy #7: Chop Your Units Into Spirals

If you’ve taught your course in the past using blocks or units, why not take that long range plan and simply chop up the units into smaller chunks. For example, you could take your first 3 days of each unit and make them one spiral, then the next 3 days from each unit for your second spiral, and so on.

The benefit here is that you will still feel like you are organized in units, but your units are just being spread out over longer periods of time.

Spiralling Starter Strategy #8: Spiral a Single Concept

Another great starter strategy was brought to my attention by Sherry Doherty and Deborah Hartmann. They suggest starting with a big idea – like fractions – or a single unit – like say measurement – and sprinkling those lessons, activities and investigations throughout your regular units as a manageable first step.

Ms. Butson also suggests starting with one important concept, but rather than spreading your lessons related to that idea throughout the course, why not focus specifically on how that specific concept connects to other areas of your curriculum and intentionally pulling that concept out as often as possible. Once you get a feel for how to do that with one concept, you move on to try doing the same with another concept. Eventually, you’ll be full blown spiralling and making multiple topic connections daily!

Spiralling Starter Strategy #9: Interleaving Activities and Investigations

Finally, the last of the spiralling starter strategies was mentioned by Dave Lanovaz. He suggests that you get started by keeping your units or blocks in tact, but spiralling activities that you might do throughout a unit with a mix from other units across the course. So while your long range plan will feel like you are maintaining the same order and structure you’ve used in the past, the activities being introduced are mixed from different parts of the course.

Seems pretty doable to me!

So, there you have it; 9 Spiralling Starter Strategies that you can use to get your feet wet with spiralling. If you’ve made it this far, that means that you must be seriously considering implementing spiralling in some capacity.

While you can attempt all 9 of these strategies, I’m going to suggest that you pick one and fully commit to implementing it. Be sure to download and print the spiralling cheat sheets included with each section in this series and come back to it for reflection and planning your next step to integrating spiralling and interleaving in your math class.

Make yourself small, attainable goals and you will find yourself confidently spiralling your classroom in the way that suits YOU and your students best.

Spiralling Starter Strategy #9: Interleaving Activities and Investigations

Finally, the last of the spiralling starter strategies was mentioned by Dave Lanovaz. He suggests that you get started by keeping your units or blocks in tact, but spiralling activities that you might do throughout a unit with a mix from other units across the course. So while your long range plan will feel like you are maintaining the same order and structure you’ve used in the past, the activities being introduced are mixed from different parts of the course.

Seems pretty doable to me!

Which Spiralling Starter Strategy Are You Going to Try?

So, there you have it: 9 Spiralling Starter Strategies that you can use to get your feet wet with spiralling. If you’ve made it this far, that means that you must be seriously considering implementing spiralling in some capacity. Awesome!

While you can attempt all 9 of these strategies, I’m going to suggest that you pick one and fully commit to implementing it. Be sure to download and print the spiralling cheat sheets included with each section in this series and come back to it for reflection and planning your next step to integrating spiralling and interleaving in your math class.

Make yourself small, attainable goals and you will find yourself confidently spiralling your classroom in the way that suits YOU and your students best.

I’m extremely exited that you’ve dedicated so much time to learn about spiralling with me. I hope you’ve found this resource useful for your own professional learning and I look forward to continue learning with you in an upcoming blog post, video or course real soon!

Spiralling Resources

Here is an ongoing list of blog posts, books and other resources that are useful if you are interested in Spiralling Mathematics or any other course for that matter. Have something to add? Help the whole community out in the comments!

People From The Math Twitter Blogosphere (#MTBoS) Who Spiral & Their Blog Posts

• Jon Orr [Twitter | Blog: Teaching With Spiralled 3 Act Tasks]
• Alex Overwijk [Twitter | Blog: Spiralling Post]
• Henri Pincciotto [Twitter | Blog: Lagged Homework | Blog: Separating Related Topics]
• Mary Bourassa [Twitter | Blog: Spiralling Post]
• Dave Lanovaz [Twitter]
• Mr. Hogg [Twitter | Blog: Spiralling Post]
• Jimmy Pai [Twitter | Blog: Spiralling Posts]
• Jessica McConnell [Twitter]
• Norma Gordon [Twitter]
• Ve Anusic [Twitter]
• Heather Theijsmeijer [Twitter]
• Dawn Butson [Twitter]

Great Books, Articles and Documents Supporting Spiralling and Interleaving

• How We Learn [AMAZON]
• Make It Stick [AMAZON]
• Interleaved Mathematics Practice – Giving Students a Chance to Learn What They Need to Know [ARTICLE]
• The Key to Interleaving: Jumble It Up! [ARTICLE]
• The Interleaving Effect: Mixing It Up Boosts Learning [ARTICLE]

Research Supporting Spiralling and Interleaving

• Interleaved Practice Improves Mathematics Learning (Rohrer, Dedrick, and Stershic) [PDF]
• The benefit of interleaved mathematics practice is not limited to superficially similar kinds of problems (Rohrer, Dedrick, Burgess) [PDF]
• Interleaved Practice Enhances Skill Learning and the Functional Connectivity of Fronto-Parietal Networks (Lin, C. H. J., Chiang, M. C., Knowlton, B. J., Iacoboni, M., Udompholkul, P., & Wu, A. D. 2013) [PDF]
• Why interleaving enhances inductive learning: The roles of discrimination and retrieval (Birnbaum, Kornell, Bjork, Bjork) [PDF]

Spiralling Frequently Asked Questions (FAQ)

Here are some Frequently Asked Questions (FAQ) regarding spiralling, interleaving and mixing math content I’ve received through the release of this 3-part video series.

If you know of a friend or colleague who would benefit from this video series, please share on your favourite social media platform.

I’m sure there are many other creative ways to start your journey to spiralling your math lessons that aren’t listed here. Please share your ideas in the comments!

What are you waiting for? Let’s get spiralling!