A Progression of Counting and Quantity
Success in mathematics begins with the development of a sense of number through counting and quantity. It may seem that children learn to count in much the same way that they learn their alphabet – by simply repeating numbers by rote. While teaching our children to count from 1 to 10, 20 or even 100 is helpful, this skill alone is not the same as learning how to count. For children to build number flexibility in primary and middle school grades, developing a strong foundation in counting and quantity is very important. When a student begins to struggle along their mathematics learning journey, the culprit can often be linked to gaps in learning from previous grades. Having worked with many students in remedial math classrooms, I often found that struggles can be linked to a lack of conceptual understanding in counting and quantity. This Principles of Counting and Quantity Cheat Sheet is designed to help parents and teachers better understand how to help their children with counting and quantity during the early years.

Want to Take This Learning To Go?
Download the 15-page printable Counting and Quantity Cheat Sheet and finish up the learning with or without internet access from your favourite device!

1. Stable Order
The first principle of counting involves the student using a list of words to count in a repeatable order. This ordered or “stable” list of counting words must be at least as long as the number of items to be counted.
Strategies that Support Student Learning
- Putting pictures of items in order from smallest to largest, based on quantity, and counting them forwards and backwards.
- Organizing objects in order, without numbers at first, then adding the symbols later.
If you observe:
- A child miscounting orally by rote or with objects…
Consider:
- Intentionally miscounting and ask the child to tell you what number you missed.
2. One-to-One Correspondence
Understanding that each object in a group can be counted once and only once. It is useful in the early stages for children to actually tag or touch each item being counted and to move it out of the way as it is counted.
Strategies that Support Student Learning
- Encouraging students to “tag” or move items out of the way while counting.
- Matching items with pictures. For example, using search and find books.
- Encouraging students to create a tally chart to count and track the quantity of food, toys, sounds (i.e.: taps on a drum), letters in a word or words in a sentence.
If you observe:
- A child playing in the kitchenette area preparing food for stuffed animals…
Consider:
- Asking how many items of food they are preparing or how many people they are cooking for.
Want to Take This Learning To Go?
Download the 15-page printable Counting and Quantity Cheat Sheet and finish up the learning with or without internet access from your favourite device!

3. Cardinality
Understanding that the last number used to count a group of objects represents how many are in the group. A child who recounts when asked how many candies are in the set that they just counted, may not have an understanding of the cardinality principle.
Strategies that Support Student Learning
- Encouraging students to show you a group of items to match a specific number.
- Ask students to count a group of items in a set. Then, explicitly ask them to show you how many objects in that group represent that amount.
If you observe:
- A child building a tower out of lego…
Consider:
- Asking if they can use the same amount of lego to create a path.
4. Conservation
Understanding that the count for a set group of objects stays the same no matter whether they are spread out or close together. If a student counts a group of items that are close together and then needs to recount after you spread them out, they may not have developed an understanding of the principle of conservation.
Counting and Quantity Tip: Avoid Rushing to Symbols
Want to Take This Learning To Go?
Download the 15-page printable Counting and Quantity Cheat Sheet and finish up the learning with or without internet access from your favourite device!

5. Order Irrelevance
The order in which items are counted is irrelevant. Students have an understanding of order irrelevance when they are able to count a group of items starting from different places. For example, counting from the left-most item to the right-most and visa versa.
Strategies that Support Student Learning
- Counting sets of items from left-to-right, right-to-left, top-to-bottom and bottom-to-top.
- Counting sets of unique items (different colour, shape, etc.) in a variety of orders.
If you observe:
- A child counting a set of toy cars…
Consider:
- Asking if they can predict how many cars there would be if they started counting from a different spot.
6. Abstraction
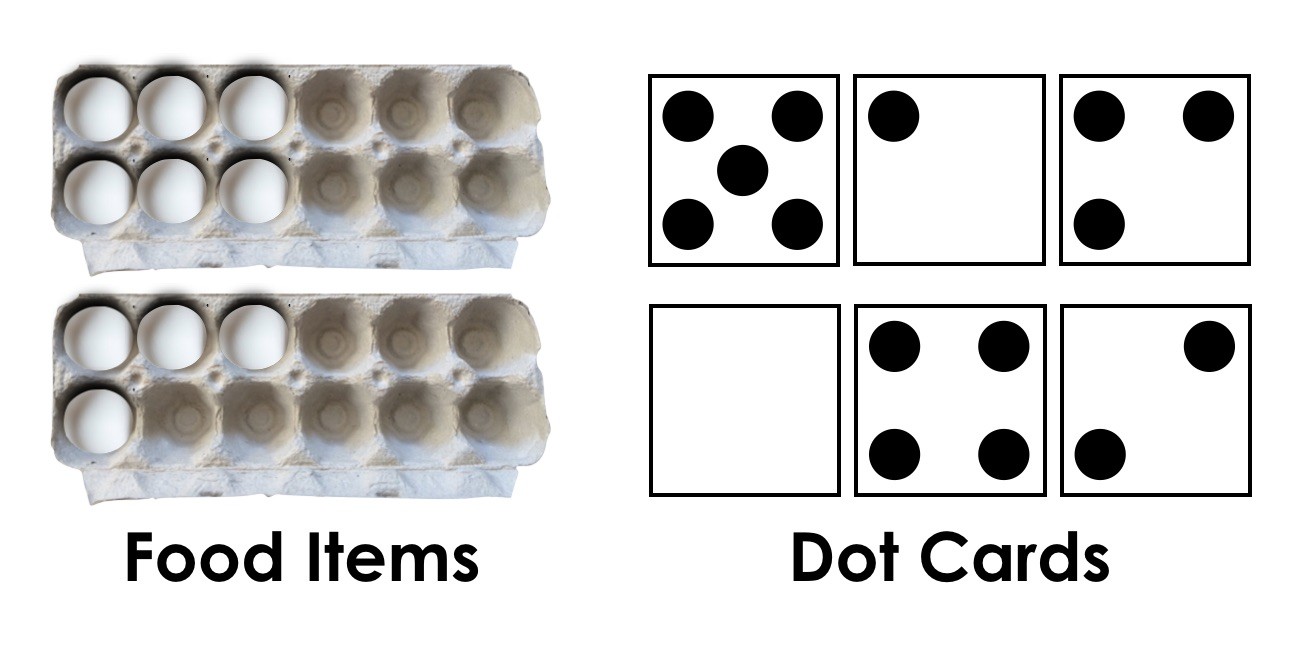
Abstraction requires an understanding that we can count any collection of objects, whether tangible or not. For example, the quantity of five large items is the same count as a quantity of five small items or a mixed group of five small and large things. Another example may include a student being able to count linking cubes that represent some other set of objects like cars, dogs, or bikes.
Strategies that Support Student Learning
- Counting non-tangible quantities such as sounds, actions, words, questions or steps.
- Matching groups of different items with the same quantity.
If you observe:
- A child playing with toys of different sizes…
Consider:
- Taking a group of 2 larger items and a group of 3 smaller items and asking which has more.
Want to Take This Learning To Go?
Download the 15-page printable Counting and Quantity Cheat Sheet and finish up the learning with or without internet access from your favourite device!

7. Subitizing
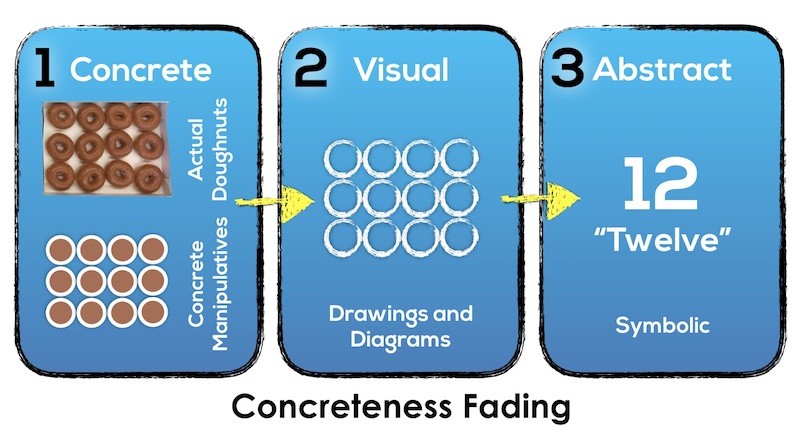
In general, subitizing is the ability to “see” or visualize a small amount of objects and know how many there are without counting. While this idea may seem simple on the surface, subitizing is actually quite complex. If we dig deeper, we can see that there are two types of subitizing that could be going on in our mind when we are learning to count called perceptual subitizing and conceptual subitizing.
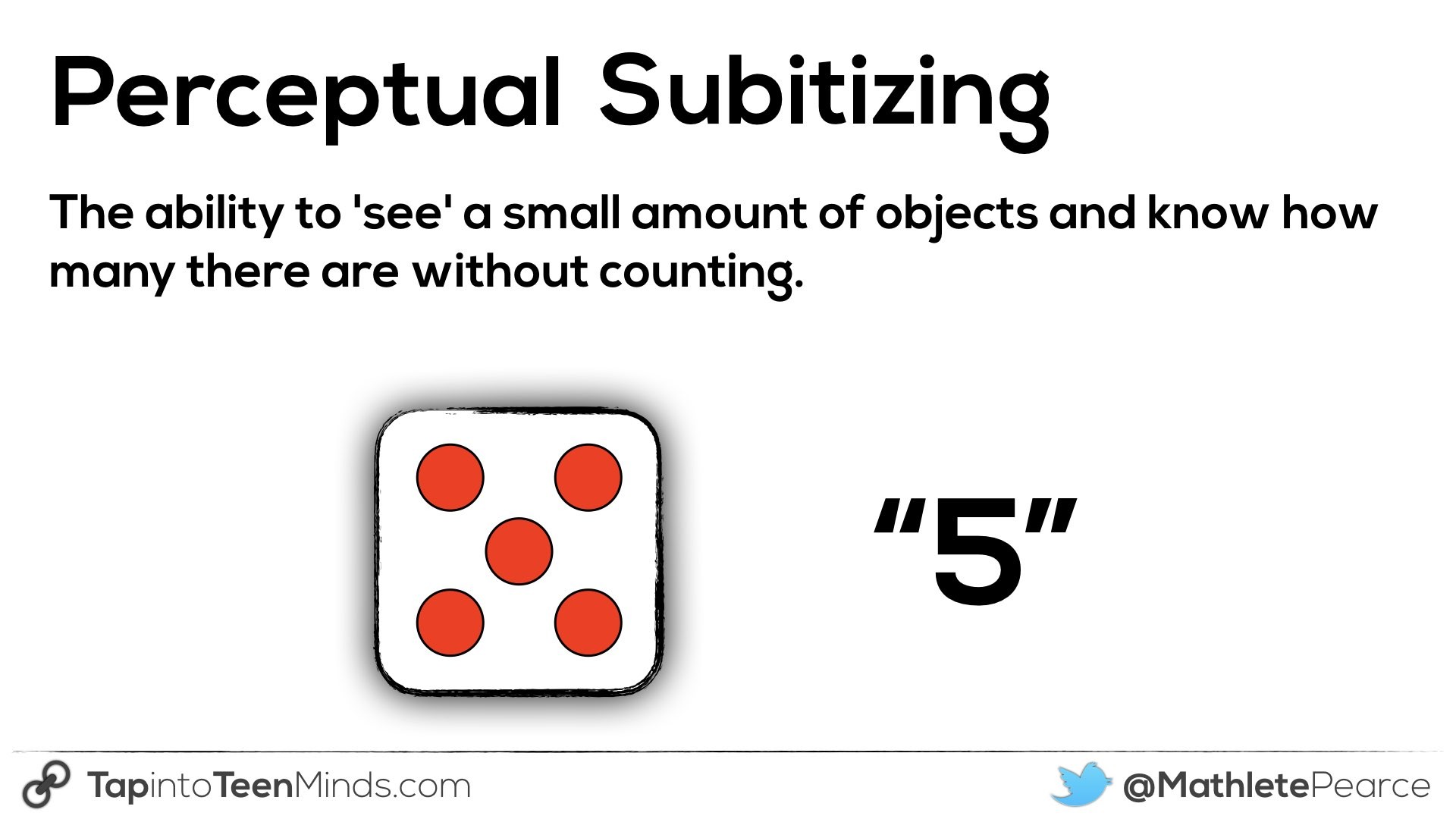
Perceptual Subitizing
Perceptual subitizing takes place when you are able to look at a group of objects and know how many objects there are without having to do any thinking. Often times, when we look at groups of 5 objects or less, we are subitizing perceptually.
Examples of perceptual subitizing could include:
- Knowing there are 3 candies on a table without counting the candies.
- Knowing you rolled 5 with a single die without counting the dots.
- Knowing there are 2 cars in your driveway without counting the cars.
Conceptual Subitizing
Strategies that Support Student Learning
- Ask children to count how many objects are in a set that is out of reach or difficult to physically tag using one-to-one correspondence (i.e.: cars in the driveway, chairs at the table, etc.).
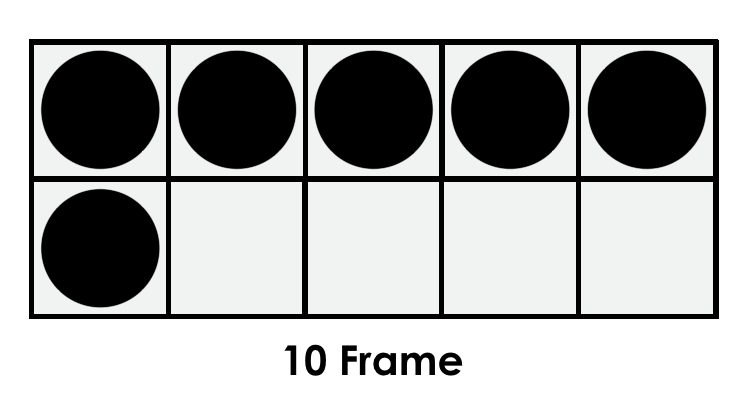
- Create dot cards using pieces of paper with small quantities of dots on each, arranged in different configurations and play matching games, war and other fun card games with them.
If you observe:
- A child playing with a small quantity of items…
Consider:
- Asking them how many items they are playing with.
Want More Subitizing Activities?

8. Hierarchical Inclusion
Understanding that all numbers preceding a number can be or are systematically included in the value of another selected number. For example, knowing that within a group of 5 items, there is also a group of 4 items within that group; 3 items within that group; 2 items… and so on.
Strategies that Support Student Learning
- Ask children to name the number that is “one larger” or “one smaller” than a number.
- Ask for a number that is “inside” the number 7.
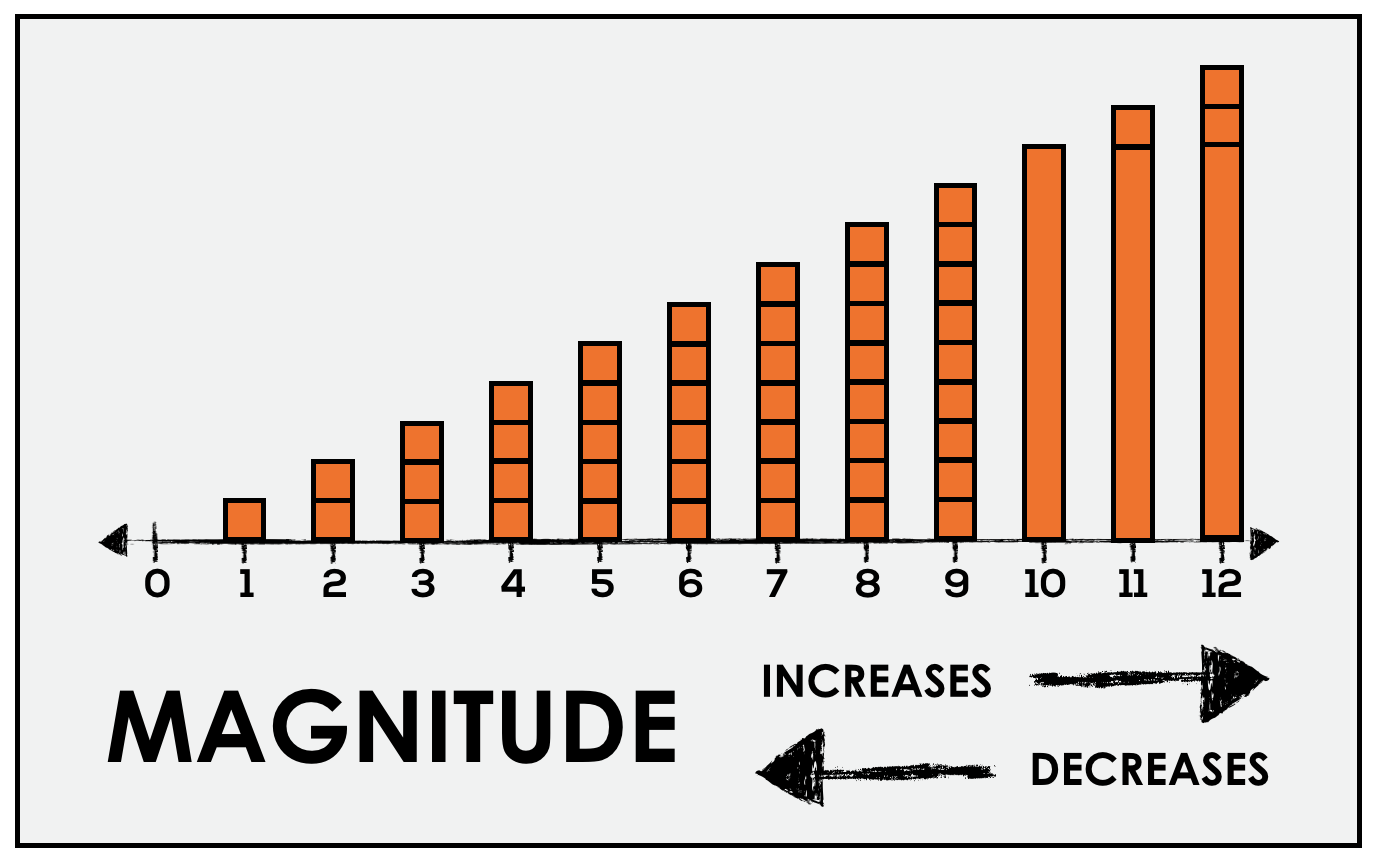
9. Movement is Magnitude
Understanding that as you move up the counting sequence (or forwards), the quantity increases by one and as you move down (or backwards), the quantity decreases by one or whatever quantity you are going up/down by.
Want to Take This Learning To Go?
Download the 15-page printable Counting and Quantity Cheat Sheet and finish up the learning with or without internet access from your favourite device!

10. Unitizing
Unitizing refers to the understanding that you can count a large group of items by decomposing the group into smaller, equal groups of items and then count those. For example, if there is a large group of candies on a table, one might choose to create groups (or “units”) of 2 (often doing this by perceptually subitizing these groups) and skip counting up by 2’s. Some may choose to create “units” of 3 and skip count up by 3’s.
Understanding Place Value Through Unitizing
Unitizing is also important for students to understand that objects are grouped into tens in our base-ten number system. For example, once a count exceeds 9, this is indicated by a 1 in the tens place of a number.
References and Resources
Online Resource
- Counting & Quantity Visuals
- Count With Your Eyes: Subitizing Guide
- How the 5 Counting Principles lay the foundation for flexible thinking in later grades
- Mathematics in the Early Grades: Counting & Cardinality
- The Principal Counting Principles
Books to Learn More About Counting, Quantity and Early Mathematics
Research
- Bermejo, V., Morales, S. and Garcia de Osuna, J. (2004) Supporting children’s development of cardinality understanding, Learning and Instruction, 14: 381–98. [PDF]
- DCSF (Department for Children, Schools and Families) (2009), Children thinking mathematically: PSRN essential knowledge for Early Years practitioners. Nottingham: DCSF. [PDF]
- Gelman, R. & Gallistel, C. (1978) The Child’s Understanding of Number. Cambridge, MA. Harvard University Press. [PDF]
- Clements, D. & Sarama, J. (2010) Learning Trajectories in Early Mathematics – Sequences of Acquisition and Teaching. Buffalo, NY. [PDF]
DOWNLOAD THE FREE COUNTING CHEAT SHEET!
















Trackbacks/Pingbacks