We’ve all heard it before; kids don’t know their math facts! While this may be true for some students, what is more important than simply memorizing multiplication facts is building a conceptual understanding of what multiplication means, how to visualize multiplication and eventually, helping students to generate their own algorithms for multiplication BEFORE they encounter any standard algorithms.

In this post, I want to dive into the math wars and try to clear up some confusion that may exist.

Importance of Math Facts

When addressing the math wars, I think it is really important for us to clear up some of the confusion that may exist around the importance of “math facts” or “multiplication tables” and whether students should be memorizing them.

In Canada, the media often paints a picture as though there is one group fighting for students to memorize math facts like multiplication tables – often referred to as “the back to basics” group and the other group – often referred to as the “discovery math group” is promoted as a group that doesn’t believe that math facts have any importance. Sadly, the picture portrayed in the media is incomplete at best.

And unfortunately, after the debate finally quiets down in the media for a while, it is brought right back to the forefront when standardized test scores or international math rankings such as PISA scores are released.

While it might seem easy to blame the Common Core for the math wars in the United States, these two extreme stances have been around for quite some time in mathematics education.

Regardless of whether your beliefs align more closely with a “back to basics” or “discovery and inquiry” viewpoint, the fact is that we all want students to know their math facts. The real conflict exists in different interpretations of what that means and how we can help students get there.

So, let’s spend a few minutes to better understand the similarities and differences of the two stances that are often portrayed in the media in order to find some sort of balance between both.

Memorization vs. Automaticity

One of the big differences I see between those who tend to side with the “back to basics” group and those who align more closely with the “inquiry and discovery” group is that of memorization versus automaticity.

When many think of the word memorization, they think about rote learning; committing information to memory through repetition, speed and without the need for meaning.

While humans memorize a lot of information by rote, this memorization technique is used optimally for memorizing information that is difficult to connect to other information we already know such as memorizing the address or phone number of a family member, Learning new information that can easily connect to our prior knowledge through rote can be truly limiting that new learning for recall purposes only, rather than for understanding.

By promoting the learning of math facts and mathematics in general through purposeful mathematical experiences, students are not only able to recall their new learning, but they can also do so with understanding. This approach to learning math facts is often referred to as automaticity.

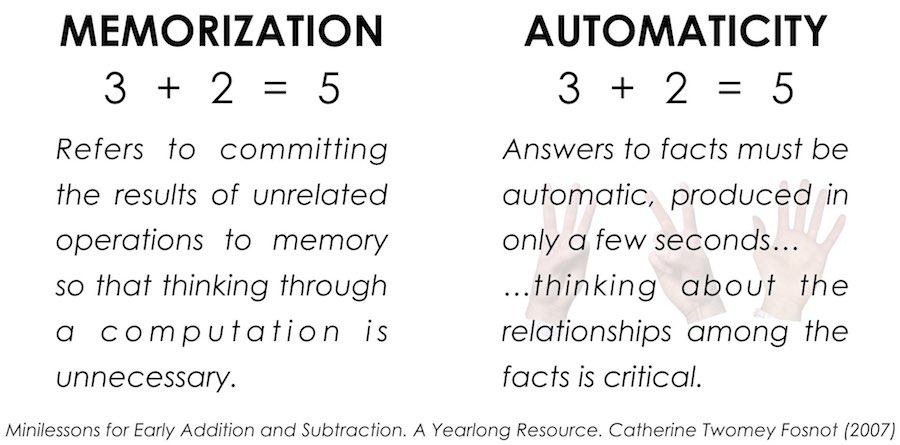
While different people may have slightly different definitions, I really like how Cathy Fosnot describes both memorization and automaticity in her Minilessons series. Fosnot states that memorization “…refers to committing the results of unrelated operations to memory so that thinking through a computation is unnecessary” while automaticity suggests that “answers to facts must be automatic, produced in only a few seconds … thinking about the relationships among the facts is critical”.

Although it might seem as though the differences are quite subtle, they can really impact how an educator might go about helping students learn their math facts. Ultimately, I believe that if we want our students to build automaticity, we will be providing opportunities to build a conceptual understanding by engaging with interesting mathematics in order to learn math facts, not the other way around.

Let’s commit to exploring interesting math in order to build math fact fluency and automaticity rather than memorizing before exposing students to the beauty of mathematics.