The Foundation and Development of Multiplicative Thinking

Proportional Reasoning is a big idea that is connected in some way to all mathematical strands and stretches across many grades in the Ontario mathematics curriculum. While many focus on the importance of proportional reasoning for students in junior and intermediate grades, I believe that we can see the early development of proportional reasoning in kindergarten and primary grades when students begin unitizing, grouping, and fair sharing. In this post, I’d like to briefly explore some of the progression of proportional reasoning across the Ontario mathematics curriculum.

Paying Attention to Proportional Reasoning

The Ontario Ministry of Education has done a great job releasing documents in the Paying Attention to Mathematics series and the Paying Attention to Proportional Reasoning document is no exception.

This document does a great job of providing a great overview of proportional reasoning from a research based perspective without getting too heavy. I will share a few take-aways below and build on some of the ideas from the document with my own spin.

Relative vs. Absolute Thinking

When students begin approaching problems multiplicatively instead of additively, such as thinking that 10 is two groups of five or five groups of two rather than one more than nine, students are said to be reasoning proportionally. This multiplicative thinking allows for students to begin comparing two quantities in relative terms rather than absolute terms.

The essence of proportional reasoning is the consideration of number in relative terms, rather than absolute terms.

Paying Attention to Proportional Reasoning Document
Ontario Ministry of Education

Which Investment Is Better?

Scenario #1: You invest $100 and it grows to $400.

Scenario #2: You invest $1,000 and it grows to $1,500.

Your opinion will change based on whether you make your comparison of the quantities in each scenario in relative or absolute terms.

If you view this comparison in absolute terms, you might believe that Scenario #2 is the best investment since you have earned more money.

However, if you view this comparison in relative terms, you might believe that Scenario #1 is the best investment since you have earned more money relative to the initial investment amount.

Proportional Reasoning Is Complex and Interconnected

As are most big ideas in mathematics, proportional reasoning is an idea that connects to many key ideas including:

• Partitioning
• Understanding rational numbers
• Multiplicative reasoning
• Scaling up and down
• Relative thinking
• Understanding quantities and change
• Spatial reasoning
• Measuring, linear models, area, volume
• Unitizing
• Comparing quantities and change

Although the ideas of multiplicative thinking begin developing in grade 1 and 2 when students are encouraged to group quantities into units and then formally as multiplication in grade 3, let’s take a look at a couple expectations in the Number Sense and Numeration strand in Grade 4 of the Ontario Grade 1 to 8 Mathematics Curriculum and some sample problems for each:

Expectation:

• multiply to 9 x 9 and divide 81 ÷ 9, using a variety of mental strategies (e.g., doubles, doubles plus another set, skip counting);

Question:

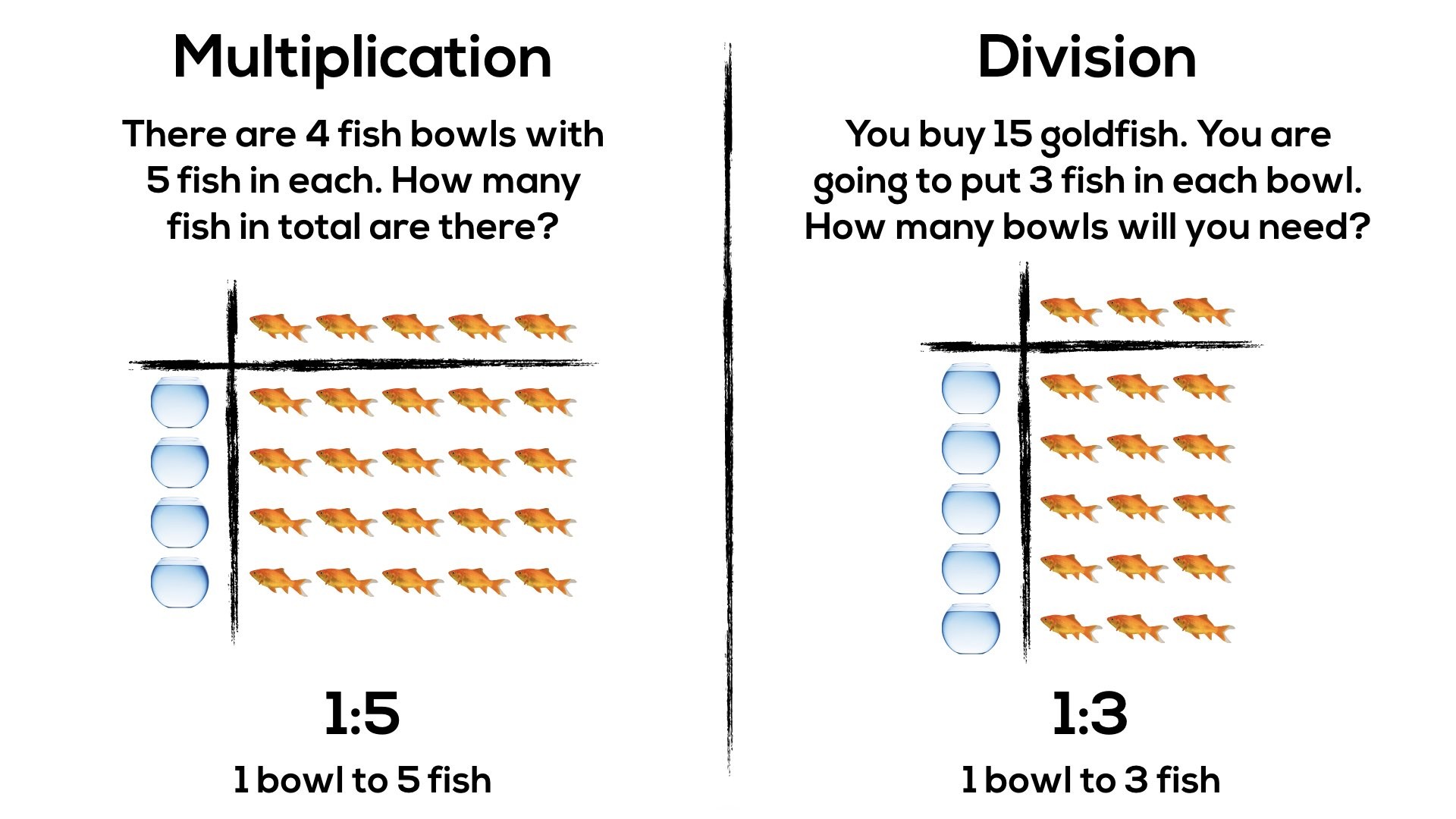
There are 4 fish bowls with 5 fish in each. How many fish in total are there?

Each bowl can be considered as both 1 bowl (unit) or 5 fish, simultaneously.

Expectation:

• divide two-digit whole numbers by one-digit whole numbers, using a variety of tools (e.g., concrete materials, drawings) and student-generated algorithms;

Question:

You buy 15 goldfish. You are going to put 3 fish in each bowl. How many bowls will you need?

Each bowl can be considered as both 1 bowl (unit) or 3 fish, simultaneously.

The First Reference to Proportional Reasoning

Near the end of the Grade 4 Number Sense and Numeration strand, we run into the first reference to proportional reasoning in the Ontario elementary math curriculum. Under this overall expectation, we see the following:

• describe relationships that involve simple whole-number multiplication (e.g.,“If you have 2 marbles and I have 6 marbles, I can say that I have three times the number of marbles you have.”);
• determine and explain, through investigation, the relationship between fractions (i.e., halves, fifths, tenths) and decimals to tenths, using a variety of tools (e.g., concrete materials, drawings, calculators) and strategies (e.g., decompose 2/5 into 4/10 by dividing each fifth into two equal parts to show that 2/5 can be represented as 0.4);
• demonstrate an understanding of simple multiplicative relationships involving unit rates, through investigation using concrete materials and drawings (e.g., scale drawings in which 1 cm represents 2 m) (Sample problem: If 1 book costs $4, how do you determine the cost of 2 books? … 3 books? … 4 books?).

Notice the multiplicative thinking and comparison of quantity in relative terms. We also encounter the formalization of unitizing through whole number unit rates. It is at this stage where we see the ground work being laid for ratios and rates. While I don’t believe it would be developmentally appropriate to make the leap to ratios or rates at this junction, I do think it is important for the teacher to be aware that the tasks students are asked to solve here are ultimately very simple ratio and rate problems in disguise.

For example, each of our previous unitizing problems for multiplication and division involving fish and fish bowls can be represented as a rate of 5 fish to 1 bowl and 3 fish to 1 bowl, respectively.

In Grade 6, we formally introduce the comparison of two quantities with the same unit as a ratio:

• represent ratios found in real-life contexts, using concrete materials, drawings, and standard fractional notation (Sample problem: In a classroom of 28 students, 12 are female. What is the ratio of male students to female students?);

It is fairly common to see a rush to the algorithm via an equation of equivalent fractions in order to meet this expectation while minimizing or avoiding the use of concrete materials, drawings and other representations.

Let’s take a look at a sample problem with some possible concrete and/or visual representations in order to promote the idea of concreteness fading as we build our conceptual understanding:

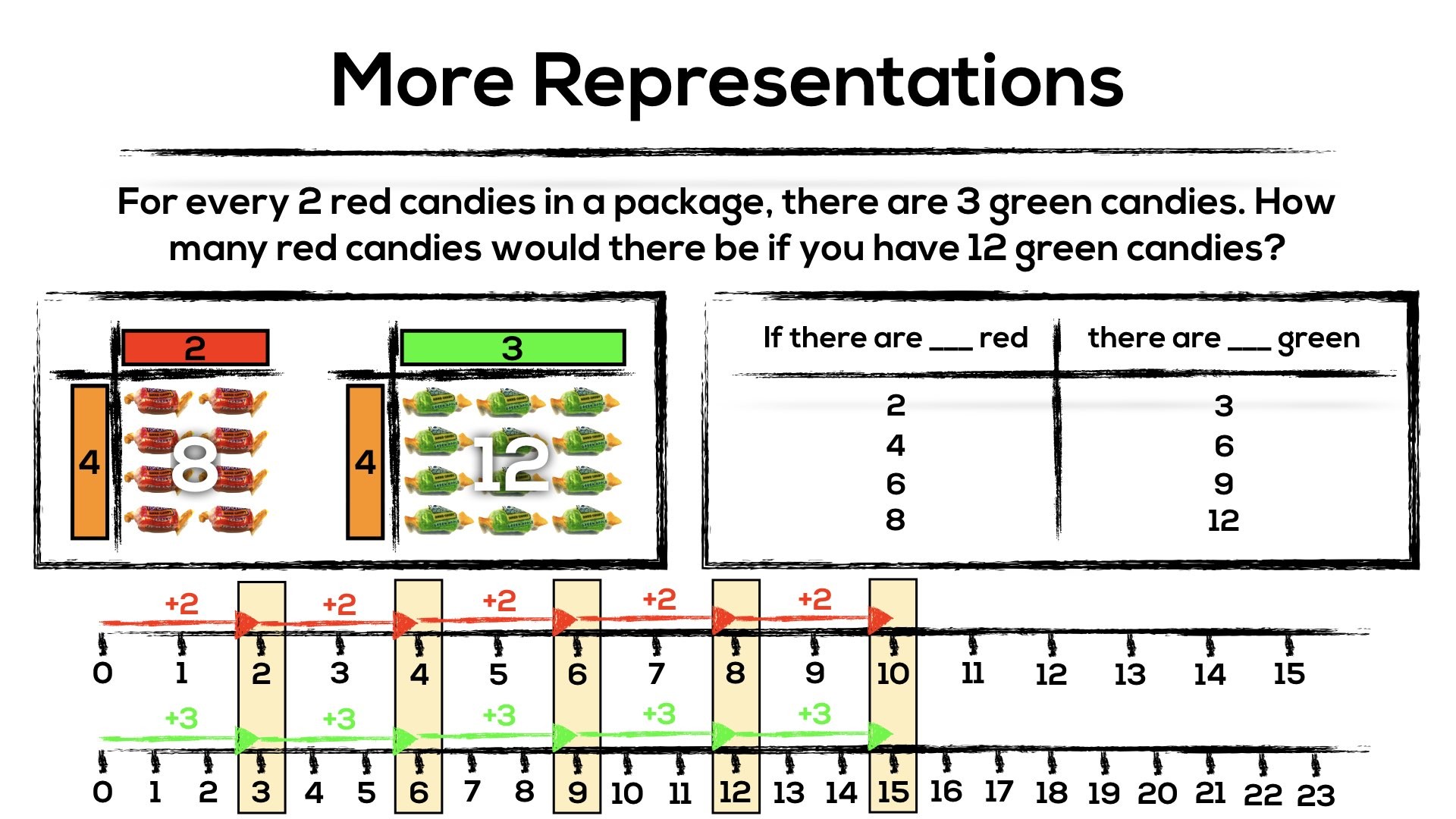
For every 2 red candies in a package, there are 3 green candies. How many red candies would there be if you have 12 green candies?

While it might be tempting to jump straight to representing this problem in standard fractional notation (i.e.: 2/3 = x/12), let’s consider some concrete and visual approaches to promote a deep conceptual understanding prior to jumping to the symbolic.

Double Array Model

The “double array model” is a representation that I feel strongly about as it builds on the idea that proportional reasoning is multiplicative and a relative comparison of two quantities. I am uncertain if I came across this representation somewhere along my learning journey or if it came about organically. In either case, I have yet to find this representation online or in common Ontario resources such as The Guide to Effective Instruction in Mathematics.

Here’s what a double-array model might look like in this case:

While I especially like the explicit connection that we can make from multiplication and division as inverse operations to proportional reasoning that a double array can provide, double number lines (or “clotheslines“) and ratio tables are also common representations that can make proportional relationships easier to conceptualize.

Making Proportional Reasoning Contextual, Visual and Concrete

If you’ve read some of my other posts or attended a workshop, you’d probably know that my vision for teaching math involves making tasks contextual, visual and concrete. So, let’s flip back to a 3 act math task I created a while back called Doritos Roulette.

Check out the act 1 video if you aren’t familiar with the task.

After much mathematical discourse amongst students, I always aim to settle on:

How many “hot” chips should we expect in a bag?

Assuming students are developmentally ready to take the leap to a symbolic strategy using a proportion via equivalent fractions, it can be useful to connect our understanding of double arrays, ratio tables and double number lines like you see in this video:

While I do believe that building a conceptual understanding through multiple representations of proportional reasoning is very important, I think it should be explicitly stated that taking this approach will not necessarily speed up the learning process. Realistically, it could take longer due to the depth of knowledge we are striving for. I’m a firm believer that anything worthwhile takes time and effort. Our mathematical understandings are no exception.

Interested In Learning More?

Why not dive into our full self-paced and online 9 module course that unpacks the “Roadmap To Proportional Reasoning” called The Concept Holding Your Students Back.

You can learn more about the course here.