For some, collecting like terms and simplifying expressions isn’t too hard a task. For others, it can be quite difficult if they are depending on memorizing the rules without any real context to go along with it.

Students may be asking questions similar to these when determining what is a like term and how to simplify the expression:

• Do I add the numbers in front of the variable AND the exponents?
• Are all terms with the same variables like terms even if the exponents are different?
• Do the coefficients need to be the same for terms to be like terms?
• and so on…

I think we’ve all used the “apples” and “oranges” analogy or something similar to make simplifying an expression with first degree terms as easy as can be:

3x + 4y + 2x + y = 5x + 5y

Although this might make things rather simple for most students, start throwing in exponents or more than one variable and then things can get interesting. This is another area where using algebra tiles can be very useful to help students visualize the algebra they are learning in order to develop a deep understanding and promote making connections as they move forward.

Some Basic Examples

Simplify:

  3x + 4 – 2y + 2x – 2
= 5x – 2y + 2

Similar to the apples and oranges example used previously, many some students may not have a problem with this. However, to get them comfortable with using algebra tiles and visualizing what expressions actually look like, it would be a good idea to introduce the algebra tiles early and often.

With algebra tiles, you can very quickly see which terms are like terms by looking at the shape and size of the tiles in each group:

Simply rearranging the tiles, or collecting like terms as we call it in algebra, can allow students to quickly understand what we are dealing with visually:

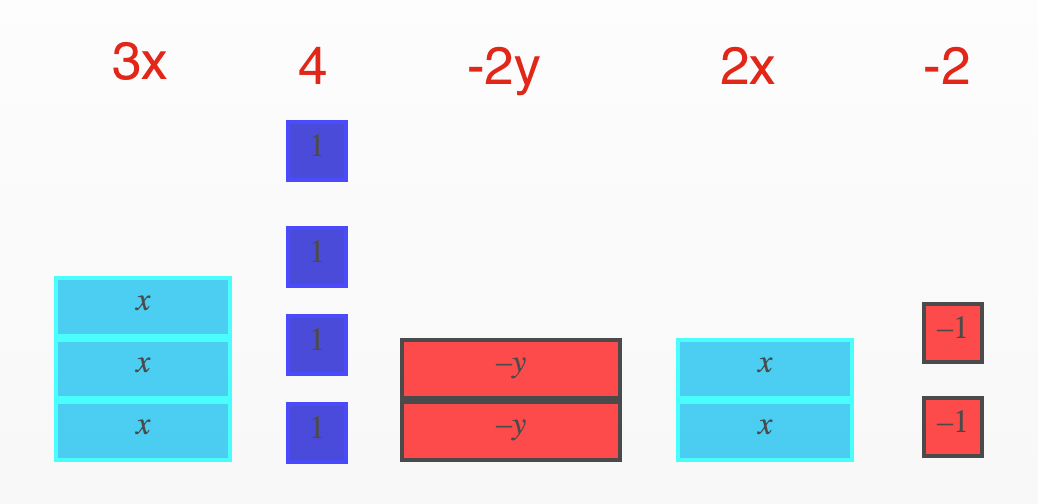
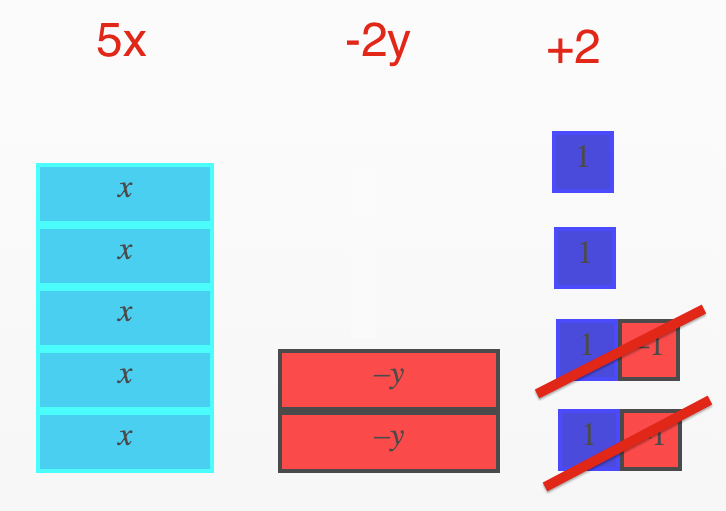
Toss in Multiple Variables and Exponents – Still a Breeze!

The previous example may not have been a question that required the use of manipulatives like algebra tiles, but it is a great place to start as the tool is only useful if the operator knows how to use it. Introducing algebra tiles on the day things get tough could make things worse as they are now trying to understand two new concepts instead of one.

Here’s an expression that has two variables and exponents:

Simplify:

$latex 2x^2 – 3x + y^2 – x^2 + 2 + 2y^2 + x $
$latex = x^2 + 3y^2 – 2x + 2 $

It can be a bit more difficult trying to identify the like terms, even if you have experience in doing so. However, with a visual, this becomes much easier and can provide opportunities to co-construct some patterns or rules for collecting like terms algebraically.

It is important to note that while we don’t want students to become dependent on the use of algebra tiles, we also don’t want them to have no other option if the algebra isn’t working for them. If students can visualize the algebra and what it looks like, they can quickly sketch or picture the expression in their minds.

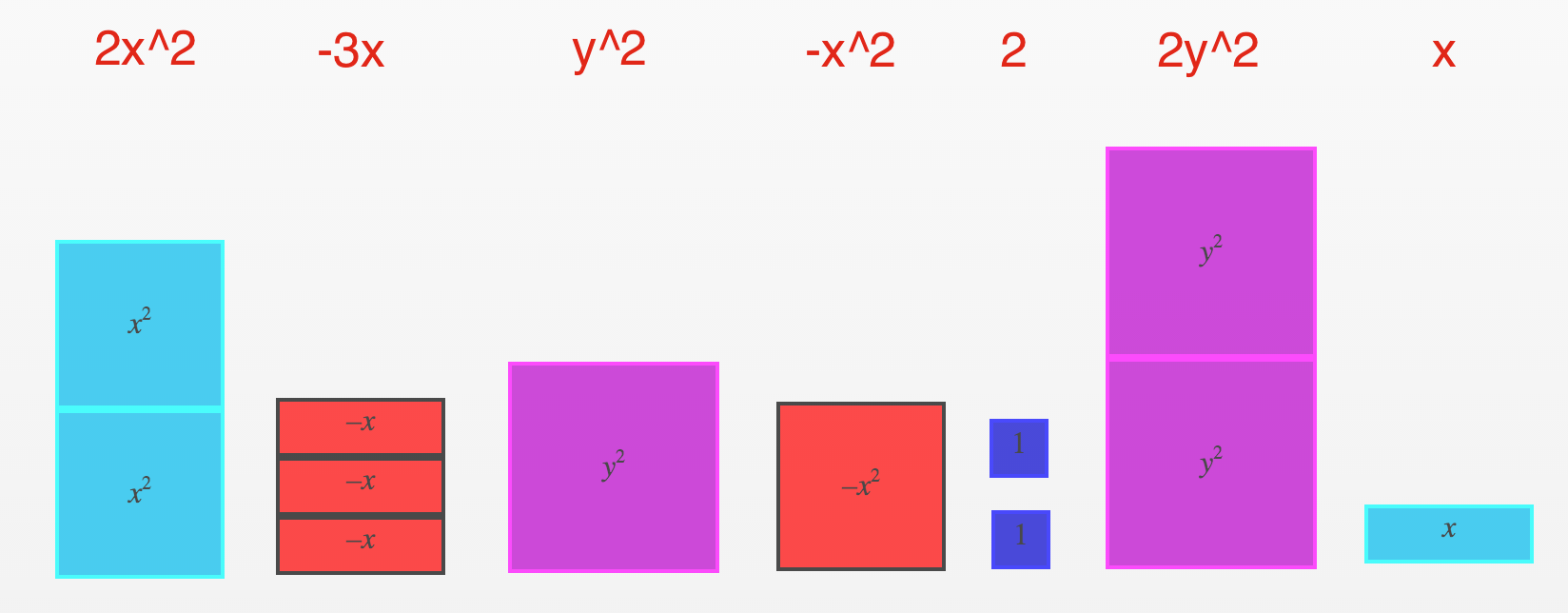
Collecting the like terms in this situation gives us the same solution as algebraically collecting the like terms:

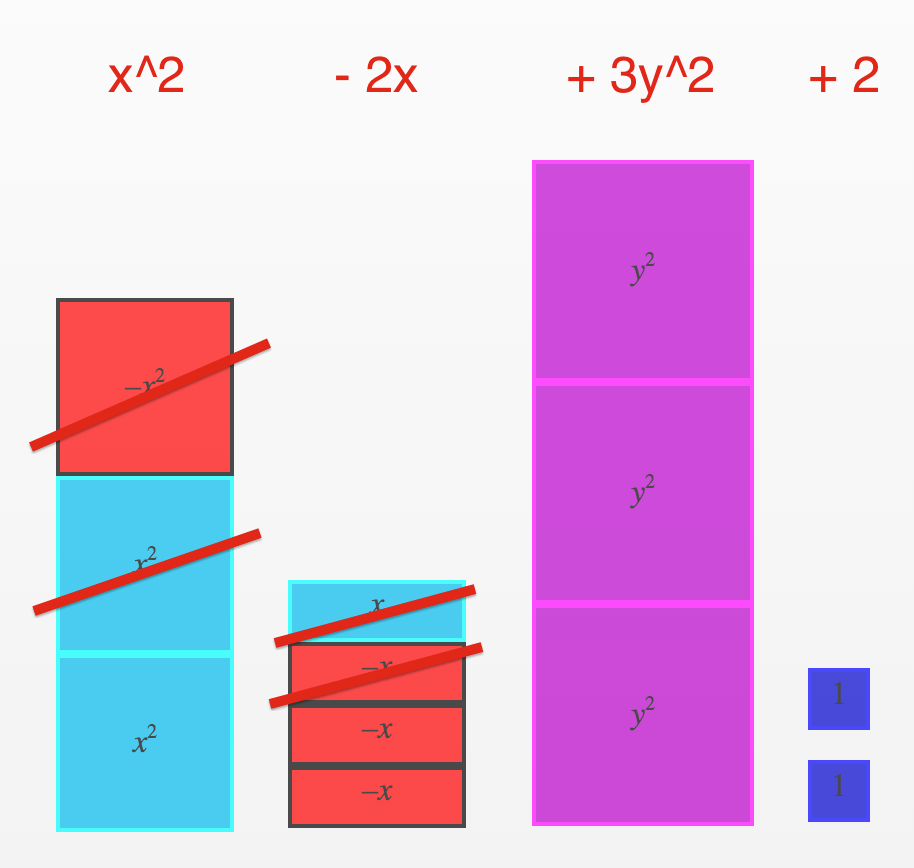
Understanding Why Algebra Tiles Look The Way They Do…

Many believe that the shape of each algebra tile was selected randomly, however this is not the case.

Each tile is based on perimeter and area.

For example, a unit tile has a value of 1 because both the length and width of the tile is 1:

Area = length x width = 1 unit long x 1 unit wide = 1 unit

The x tile and x-squared tile follows the same logic:

Area = length x width = ‘x units‘ long x 1 unit wide = ‘x units‘

Area = length x width = ‘x units‘ long x ‘x units‘ wide = ‘x-squared units‘ squared

Similar logic can be applied to the ‘y tiles‘ and ‘y-squared tiles.’

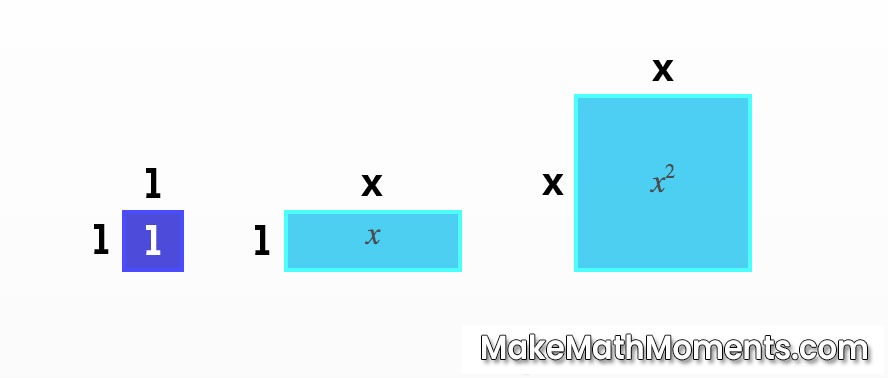
This also means that we can have an ‘xy tiles‘ where the width is an unknown value, x, and the length is a different unknown value, y. Finally, you could also extend this same logic to volume by considering 3-dimensional objects; namely, rectangular prisms.

I intend to continue posting about algebra tiles and their use in the classroom. As I do, I will also introduce some interesting algebra tiles such as ‘xy-tiles’ and ‘xyz-tiles’ to help you extend this concept to more deep applications.

How are you using algebra tiles? Please share with us below!