Episode #122: Building Flexibility: An Interview With Michelle Rinehart
LISTEN NOW…
This is Michelle Rinehart from HowWeTeachMath.com. Michelle is an innovative educational leader who pushes us to take action to empower female students to take risks, encourages us to add math talks to our daily routines, and how you can shift your practice in manageable ways.
You’ll Learn
- How to empower female math students to become risk takers.
- Why math talks are necessary for high school students, not just elementary students.
- How to shift your practice in manageable ways.

FULL TRANSCRIPT
Michelle Rinehart: Start with your why as a really important thing, I think as like a first step. Once you're clear on your why, what do you want to come of this? And then that will help drive your follow through on it. But then what you're really looking for are specific examples of what would this look like at my grade level? I think that's so incredibly important, especially for secondary teachers is to see not just Number Talks which are problems specifically about computation and with numbers, but in Math Talks, we move-
Jon Orr: This is Michelle Rinehart from howweteachmath.com. Michelle is an innovative educational leader who pushes us to take action, to empower female student to take risks, encourages us to add Math Talks to our daily routines and how you can shift your practice in manageable ways.
Kyle Pearce: Stick around to hang out with us and our good Canadian transplant, Michelle Rinehart, you surely won't regret it. Let's cue up that music.
Welcome to the Making Math Moments That Matter Podcast. I'm Kyle Pearce.
Jon Orr: And I'm Jon Orr, we are from Make Math Moments. We are two math teachers who together...
Kyle Pearce: With you, the community of educators worldwide, who want to build and deliver math lessons, that spark curiosity...
Jon Orr: Fuel sense-making...
Kyle Pearce: And ignite your teacher moves. Jon, are you ready to dive in with our wonderful Canadian friend who is now living in the South of the United States in Texas, our friend, Michelle. You ready to go here?
Jon Orr: I am. I am. But before we dive into our talk with Michelle, we want you to do a couple of things for us. One is whatever you're doing, we want you to stop. We want you to snap a pic of what you're doing. Share that with us on Facebook, share that with us on Twitter or Instagram, let us know what you're doing while you're listening to this episode. And the second thing Kyle is, we want you to leave us a review on Apple Podcasts.
Kyle Pearce: Yes. We read all of the reviews on Apple Podcasts. And right now we want to share one of those with you. This one is from West Coast, Rebecca on Apple Podcasts. She says, "The support I need to be the teacher I want to be. Have you ever received advice and it just felt right? In your heart, you already knew it, but you just needed a friend to bring it to the forefront. That's what this podcast is for teaching math. Kyle and Jon have helped me to explore my values as a math educator. They've given me concrete steps to teach in an authentic way that inspires learning and joy in my students."
Jon Orr: Wow. Isn't that fantastic? Nothing energizes us more than hearing comments and reviews Just like that one from West Coast, Rebecca.
Kyle Pearce: Yes. So you've taken 10 seconds to hit pause. And actually you don't even need to hit pause. You just take that phone out of your pocket, scroll down in your podcast app and give that review. A rating and review really helps us to reach an even wider audience. So do us that quick favor. It would mean the world to us.
Jon Orr: All right. Enough from us. Let's get on to this fantastic conversation with Michelle. Hey there, Michelle. Welcome to the Making Math Moments That Matter Podcast. Kyle and I are so excited to have you on the show today. How are you doing down in Texas?
Michelle Rinehart: Hey, Jon, thanks so much for having me. I am so delighted to be here as well. We are doing well. It is hot, but that's Texas. So, yeah, summary.
Kyle Pearce: That's awesome. Well, you know what? We're going to have you dive in and tell us a little more about yourself. We know you and I don't know, you said Texas and Texas is great and all, but I'm wondering if you could dig down a little bit and tell us a little bit about were you born in Texas? So this is kind of leading question here.
Michelle Rinehart: But you know the answer, Kyle.
Kyle Pearce: I don't know. Yeah, I don't know. Me and John being where we're from, us little Canucks here. I'm wondering, tell us a little more about where you're from, how you got into education. What's your role? What are you doing now and how did you come into that role or that place you're in now in education?
Michelle Rinehart: Yeah. Great Leading question. Proud dual citizen here. So I've been in Texas for 13 years, but born and raised in Ontario, Canada. Did my K-12 schooling just outside of London, Ontario. I did my undergrad and teacher's college in Ontario at Queens University before moving to Texas after that. So yes, definitely have Canadian roots. Talking to y'all just makes me feel so at home. It makes me feel like I'm talking to family and friends from back home. It's wonderful. So to give you a little bit of a feel for where I'm at now, so my history in the US, I've been a high school, math, and science teacher. I've been a regional education specialist across an area of West Texas serving 40 different schools. But currently, I'm a full-time doctoral student at Harvard University at the graduate school of education where I'm working on training to become a system level leader, and really thinking about what does it look like to lead our schools into the future and not just to lead them, but really to transform them, to be what we want them to be.
Then how did I get here? That's a long story, but I'll just pull out a couple pieces that I think are really interesting and particular to the work I'm doing now. When I was graduating high school, just outside of London, and I was thinking about what comes next for me, I was a first generation university student or going to be a first-generation. Second to my family after my older sister. I loved math and physics, but I had no idea like who actually used math and physics in the real world. What can you do with that if you love that?
Jon Orr: Yeah. For sure. You just be a teacher. I just heard it's really good.
Michelle Rinehart: I really didn't know. So I went to my guidance counselor. I said, "I love math and physics. I want to do that my whole life. What could I do? What kind of jobs to use that?" And she told me, "Teaching. You would be a great teacher." So I said, "Okay." So I applied to Queens, got into their math and physics program into their concurrent education program. And it wasn't until my second year of that program that I came to realize that the advice that I received as an OAC student or a grade 13 student, or I have to like translate into American, but like at the senior if you will.
Kyle Pearce: Yeah. They're like, "Grade 13? What the heck."
Michelle Rinehart: Yeah. That's a whole other conversation. But as a senior in high school was actually gender biased where I came to realize that there were two young men who I graduated with, who also loved math and physics, and they ended up in engineering programs. And here I was, top student at my school, valedictorian, had a love for these two subjects. And what I've been coached into is education.
So for a long time in education, I kind of had this like... It wasn't a love hate with the profession, but it was like a love tension where I like loved everything I was doing in the class, like loved how I was serving kids, loved the relationships, loved how I was empowering students. But I had this tension where I kind of felt like, "Am I in the right thing? Did I get coached into the right thing? Or could there have been something else for me?"
So I had that tension for a long, long time throughout my teaching career. I remember thinking like, I could have been an engineer, I could have been a rocket scientist, or I don't know what. This is so interesting how this came full circle. It wasn't till just a year and a half ago. So about 12 years into teaching that it was the night before my interview at the Harvard graduate school of education, and I was going through all my notes and just like over-preparing, right?
I came across this quotation from Dr. Deborah Jewell-Sherman, who had ended up being one of my professors at Harvard. She was encouraging people to really realize how difficult education is and how difficult educational leadership is like really transforming these systems. She had a sentence where she was encouraging people if they were kind of thrown off by those challenges to pursue a different field like rocket science, because it was easier? It just so struck me and like, "Y'all know you're in it, right? You know how difficult this field is, both from the perspective of day to day work, trying to stay afloat, trying to have an impact while also trying to change the system that we're working in, and trying to make things more impactful and equitable?"
So now I'm very much in like a love, love relationship, both with the profession, but also my place in it, because I know that we need our best and our brightest in education. And we do. We have that. So it has just given me a whole new perspective in terms of education as a profession and what we can do.
Jon Orr: I just wanted to touch back on a couple of things that you brought up. First off, I wanted to give you a shout out as a Queen's Golden Gael.
Michelle Rinehart: Yes.
Jon Orr: I also went to Queens. So I did my teaching program at Queens. I went to like Waterloo, but I was at Queens for the year at McArthur College where we probably were in or had some similar teachers. So yeah, that's one shout-out there for sure. But I did want to just ask you about this, this idea of you being coached in a teaching. I'm wondering, like, do you feel like you were coached into teaching because you were a woman or is it something else? You had mentioned that these other guys they had the same love for you all of a sudden became engineers. Do you think you were pushed that way because you felt like that person was not saying you could be an engineer? What was your feeling about that?
Michelle Rinehart: Yeah, great question. So I think there are definitely two things at play. I think undoubtedly gender bias, whether it was conscious or unconscious, I think that both still exists very much within our system was definitely at play there. I think another thing that was at play, which might have been kind of unbeknownst to my guidance counselor, I actually still don't have a term for this. So if someone listening has a term, let me know on social media, because I'd love to be able to describe this better. But I think there was also this very real gap based on where I was coming from.
So for example, my father was a farmer and my mother started in an entry-level position at the hospital. And by the time I was graduating was beginning to kind of work into lower-level management or whatnot. And most of the people we knew were farmers. I didn't know a ton of different careers. I didn't even know what an engineer was until my second year of university.
So I had this very real like knowledge gap about what was even possible. And I'm not sure that my guidance counselor knew that per se. So she might've kind of believed if you will that I knew all the possibilities and felt like education was a great fit. Now, on the other side of it, I feel like education is a great fit. I am in the right place. I am doing what I was called to do. Another thing that is so interesting to me now about ending up in education, I'm incredibly passionate about gender equity work in general, but specifically for women within leadership positions.
And through this whole process, I've ended up in the field education that has the largest gender equity gap between its workforce and between us leadership. That's not an accident. I feel like I'm here on purpose to empower women to lead at all levels within education and to lead as themselves. So that's a little bit more about why I think this was all part of a plan.
Kyle Pearce: It's so interesting like when you think about bias and you think about all of the unconscious biases that we all have, regardless of how intentional we are, or how reflective we are on it. So I'm thinking about the role of guidance counselors, for example, and I have many stories where I think a guidance counselor thinks they're trying to help as many students as possible, but oftentimes sort of shut certain doors based on a very surface level understanding of the student that they're working with.
So I'm happy it worked out for you being that you love where you are and what you're doing. But on the other hand, you just wonder about how many students out there are looking to adults to help them make choices and decisions. I don't know if we could ever be really qualified to give advice, but rather stay, I guess, more curious and allow students to kind of be coached into their own decisions on where they go. So that really resonated with me. I've got to know though, Michelle, we know you, I think everyone listening from outside Canada is always like, "Oh, do you know Tom from Canada?" Right? Everyone knows each other.
Michelle Rinehart: Yes.
Kyle Pearce: But of course we know Michelle from Canada. So my wonder though is like take us back because I'm picturing where you are now. And there's probably a lot of people listening, going like, "Wow, Michelle is doing some pretty incredible thinking around education, around mathematics, around your role and the role of the gender bias that's at play in education, but in so many different sectors as well." Take us back to your time as an educator. Let's talk about early Michelle, because I think it's really important for people to kind of understand that. I don't know. For me anyway, I was a very different teacher at the beginning of my career. And we talk about that a lot on this podcast. So take us back to early Michelle. What was early Michelle like in the classroom as a math educator? What was it look like, sound like? Take us a little bit down that journey of maybe transformation or made you arrive at where you are today.
Michelle Rinehart: Yeah. I love this question because someone I follow online was sharing recently like, "We need to stop comparing our chapter ones to somebody else's chapter seven." Right? So thinking about like, "What did my chapter one look like?" And it was not pretty. Or now I say that, and I think that that's a true mark of growth is if we look back, I think at every kind of chapter we get to later in our life, we should look back with like a bit of regret about what we did before because we didn't know what we didn't know.
So when I first started out, what was such a blessing to me was that in the Canadian system, you come out with two teachables. So I came out both as a math and as a science teacher. Which is a little different than kind of how teachers are trained, particularly in my part of Texas. But that was a blessing to me because I was teaching math and I was teaching science. I was teaching science in this very engaging hands-on problem. Conjecture. What do you think is going to happen? And then experiment with it, see what it happens and then formalize it later. Right?
Very much this idea of like a three-act task is inherent to science. It's kind of this five E, engage, explore, and then explain methodology. So that's how I was teaching science. And then I was teaching math in this very traditional way. I had been taught of here are three examples. The first one's really easy. The second one is medium. And the third one is like, "Ooh, watch out for one of these in homework." And then I'll give you all some time in class to work on the 25 problems we're going to do for homework or whatnot, and watch out for the last three on homework, because they're the word problems, right? Very traditional kind of style if you will.
At the end of my second year of teaching, when I was switching districts, one of my students gave me what I thought at the time was like the highest compliment. She said, "We're so sorry to lose you." I've been teaching calculus. She'd been one of my calculus students and she said, "You're such a good teacher. You could explain calculus to a three-year-old."
I remember being so proud of that comment at the time. Now, that I'm a mother, I realized I can explain nothing to a three-year-old. There's no convincing these children around here. But also I realized that that was rooted in what I thought math teaching was, which was very clear explanations. If you can just clearly explain something well enough, that's how you teach it. And in my third year of teaching, I ran into this cognitive dissonance where I realized that how I was teaching science, about exploring something and acknowledging the kids already knew something about this and could figure some things out before I would formalize or lay it on top of it, that was fundamentally different than how I was teaching mathematics.
They actually represented different pedagogies that represented this idea of kids can make sense kind of my science teaching versus kids have to be told my math teaching. So then I began to wonder, what would it look like? What would it look like to do that in math? And I had no ideas, right? I was like, "I don't know. I just know this one way to teach math." What would that begin to look like? So through a series of, I guess, professional learning journey, et cetera, but really fueled by this cognitive dissonance of realizing that I was thinking about these same students. I was teaching in a small rural district. So I was teaching the same kids, math and science, but I was treating them fundamentally differently in my pedagogy. What would it look like to kind of shift my math teaching to look more like my science teaching to honor that I kids could make sense of mathematics.
Jon Orr: That's a great realization. And I think I'm just going to push you a little bit here into saying like, "What did you do next?" Listeners of the show, obviously, they're listening to this show, so they're invested in mathematical change and mathematical good ideas, and we're going to get into all of that. But I'm wondering before we get into, in all the resources that you are providing to teachers, what was one thing that you did to make that change happen for your students?
Michelle Rinehart: Yeah, great question. So I still remember the moment it kind of happened. It was a fall of my third year and I'd gone to, I don't know, workshop somewhere. It was the first time that I had seen math practice that looked different than traditional textbook, page whatever, inaudible. It was someone who was thinking about review structures that looked different than that. So she had designed some scavenger hunts and some different activities, and some collaborative activities that got students talking about their math while they were doing it.
It was literally an aha for me, that math didn't have to be rigorous or fun that it could actually be both. Whereas up to that point, I thought it either had to be rigorous or fund/fluffy. So it really got me thinking across class teaching all high school courses at that point all the way through AP calc about how you could use these structures, whether it's scavenger hunts, mazes, puzzles, different kinds of structures that makes the activity more engaging for students, but also get students talking and collaborating about mathematics.
That's not something I had known how to do previously. So that was such a great next step for me. I love this idea of, yes, I didn't yet have a vision for what I wanted my math classroom to completely look like, but this was a really great next step that I could step into to move towards an engaging student centered math classroom that I wanted. So that was a like first step that really kind of unlocked things for me and got me into the next part. Another thing was thinking about opening structures differently and thinking about types of questions that I could ask students that would pull out, what do they already know about this, that would position students as mathematically competent to be able to pull on what they know and share and make connections.
So that really has paved the way into a lot of the work I've been doing around math talks, which are a routine kind of a spinoff of number talks that have students solve problems and/or come up with different ways of representing or different equivalencies, et cetera, within like a short five to eight minute routine at the beginning of class.
So that was another kind of next step where I wasn't necessarily fundamentally changing everything about how I was teaching. That felt like too big of a next step for me. But I could change how we practiced for 15 to 20 minutes. Then I changed how we warmed up for the first five to eight minutes. All of those kind of like led me along this progression to really rethinking how I was approaching math pedagogy.
Jon Orr: I'm so glad that you have kind of pointed out a couple of things, especially about this way we view comparing ourselves to people. You just finished saying, we didn't jump from one to the other. It was like this small change you could make now that you don't know what your class is going to look like down the road, or maybe you did, but it was like, "I can't get there right away. I have to make a small change incrementally to get there." I think we missed the mark on that. Like you had mentioned before, that great quote about stop comparing your chapter one or chapter sevens.
That reminded me of another one of... Especially, when you're looking online on social media, that people are comparing their worst 80%. You think about your worst class, and you would think like, "This is my class," but you always see people's best 20% online. Right? So you're comparing your worst 80% of their best 20%. You can't help but feel inferior, and you're not there. Or your chapter one versus chapter seven. I think you've done a great job here reminding everyone that it's a journey. And just because we're doing this now, doesn't mean that you can't get there, but it's going to be a slow, incremental process.
Kyle Pearce: Yeah, absolutely. Before you had mentioned a number of great things. We want to talk about some of these routines and math talks in particular. Jon, you just reiterated a few of the things I was thinking as well just this idea of, again, even thinking if you're a parent, anyone who's listening as parents like we're so hard on ourselves as parents because not only do you as a teacher often reflect on your worst class of the day, oftentimes it's like your worst moment, right?
It could be one interaction where it didn't happen the way you had wished. And it's sort of like that can change the trajectory of your mood, your mindset for the entire day. It's almost like nothing else that day was good. And in reality, it's not quite like that. That 80%, 20%, you could probably say 99% to someone's best one, right?
It's really that dramatic. So before we get too deep, we are rocking here. By the way, Michelle, you can tell there's some Canadian vibe here happening, and what's feeling super smooth. But before we get too deep, I want to go back. You had your memory of how math class should be done, right? Our understanding based on our own experiences, based on sort of just our own perspective of this is the way it's done, really, really reminded me. And I know, Jon you'd probably agree because we have very similar experiences in this regard of how math class happened to us as students.
I'm wondering, can you go back and go into that memory bank as a student in math class and describe a memorable math moment? So when you think of math class, not necessarily as a teacher, although some people do decide to go that route, I'm thinking more like as a student, is there a memorable math moment that sort of pops into your mind that you'd be willing to share with the math moment maker community?
Michelle Rinehart: Yeah. I have two that come to mind. One as a student and then another actually as a teacher. So I'll start with my student one first. As I shared, I loved math all throughout school, but what I came to realize, not in the moment, but later is that I was actually loving school math, which is not in my kind of experience, if you will, was not at all what real mathematics was about. So I very much loved this. Okay. Here's this type of problem. Here are all the steps. Now, replicate them perfectly and neatly and win all the prize. That's how I kind of thought about mathematics, and that's what I thought it was.
So in high school, then there was this opportunity to go join a math club at a neighboring university. Actually, it was at Western in London. I was like, "Okay, that would be fun." I thought that would be a really fun thing to do. So I talked to my parents into driving me in. I went to the first session and I hated it, like literally hated it because they would give us questions and they wouldn't tell us how to do them or just like figure it out. I can't even put into words how I felt, but I felt so stupid in those moments. I felt like, "Oh my gosh, I don't actually know how to do math at all."
What I didn't realize I was running into was this juxtaposition, if you will of what I thought math was, this school math versus what math actually is as this creative discipline. So that stuck with me. And even still, I ended up taking a major in mathematics and then in my undergrad realized, "Oh my goodness, math as a discipline is so much more than what I thought it was, and I can do it."
The second moment where I began to realize that math was more than I thought it was, it was my second year of teaching in Texas. I had my Canadian or Ontario teaching license kind of translated, if you will, into Texan to get a Texan license, but I had to take a certification test. So they had that down here that I had to take. So I'm taking this certification test over secondary mathematics, and there was this question on the certification test.
It had a picture of a triangle and it said, "Okay, if you kind of tear off these three angles of the triangle..." I know that y'all had done this activity, and you have seen on websites as well, I'd never done as a teacher or a student up until this point. But I saw for the first time in this test, if you tear off the three corners of this triangle and kind of position them around this vertex or whatnot, what will happen? I remember sitting there like testing, there's like a proctor walking around and I literally had like an exclaim out loud moment where I was like, "Oh my goodness." I was like, "Oh my goodness. They would make a line. They would make a line." And the proctor literally like walks over to me and she's like, "Is everything okay?" I look at her and I remember thinking everything is not okay. I remember looking at her and being like, "Everything is fine and fantastic."
Kyle Pearce: My whole world is changing.
Michelle Rinehart: Yes. And I wanted to like tell her in that moment, "Did you know? Did you know you can tear up the three vertices?" I'm going like, "Lay them out and they make crosstalk."
Jon Orr: They're like, "Yes, we wrote the test."
Michelle Rinehart: No. She was the proctor administering all different subjects. Right? She did not care. She literally thought I was having a problem with the platform or something. I just remember thinking... Again, at that moment I had an undergrad in mathematics, but I was a very accomplished like mathematician, if you will, yet, I didn't know. I didn't know what I didn't know. It was in that moment where I realized that so much of what I had come to know about mathematics was procedural, and really devoid of the real meaning.
There was so much more to mathematics that I could understand and that my students could understand if I began to see mathematics in this like multi-representational kind of approach. So those are two moments that literally have stuck with me. And they might seem negative, but it really to me was this awakening where I began to realize that how I was thinking about mathematics was too limited and was actually like an insult to what mathematics is as a discipline.
Kyle Pearce: No, I saw them as both being positive because of what you just said there as an awakening. Your example about the three angles forming 180 degrees was mind-blowing to me, but I remember reading it in a textbook, like while I was studying for like, how do I teach the angle sum theorem of triangles? That was an awakening for me in the sense where I had that love, hate relationship, all of a sudden with my past high school and elementary career as a student. I'm like, "Why didn't I learn these things? Why is it taking me to study it a little bit in depth?" That was where the vow comes out to be like, "I'm going to make sure my students see this kind of stuff." So let's keep going on this energy you're totally bringing to the podcast on your excitement for mathematics.
You mentioned Math Talks earlier, and I want to kind of dive in on that a little bit in detail here, because I think our listeners deserve to know all about this. When people think about Math Talks or Number Talks, they think... I think, generally as I'm a high school math teacher, when I talk about this to other teachers, especially in say my school or my district, I think people think that's an elementary kind of thing. That's for elementary students. Tell us more about that. What are Math Talks specifically and why are they actually good for high school students?
Michelle Rinehart: So when I first kind of came upon this idea of similar thinking was exposed to Number Talks as a really powerful structure at the elementary school level for a number of reasons. A, acknowledged and built upon the mathematics that students already know, right? Our students are not blank slate. They come in with the ability to make sense and with many mathematical ideas already. So I loved that component of it. I also loved the focus on having students talk. That was another thing that I wanted to do as a teacher when I wanted to kind of shift my instruction. But I was like, what would that even look like? How do I get my students to talk about mathematics? So I loved that component as well.
A third component is, and I kind of alluded to this earlier, it was a short instructional routine. So it was something I could try out. I could even try out over like a number of weeks without giving or sacrificing. I'm using air quotes here. Sacrificing a huge chunk of my class time to something that I wasn't sure if it was going to work. Right? So I could try to kind of shift my practice and in this really manageable way, in this five to seven-minute routine.
So all of those things, got me really excited for like, "What would this look like?" The other thing I loved about Number Talks is that it was all about students using their minds. So mental math, but not necessarily in this way of like, "You have to do everything in your head. You can't write anything down." But more so like using your mind to solve problems. So a colleague and I, her name is Amy Hoelscher. She's a teacher here in West Texas. We were both regional education consultants at the time at one of Texas's education service centers, kind of a service agency that serves multiple school districts here. Kind of like a school board in a way in Ontario.
We were thinking about, what would this look like? What would it look like? What would the problems look like at a secondary level? How could you do this where you could get students talking about and thinking about problems within a relatively short context? What we found is a lot of people had been doing work in this space or on the periphery of this space. So some examples that come to mind are things like coming out of Ontario, which one doesn't belong, right? Wodb.ca, where you could literally be looking at four different mathematical artifacts or representations that works kinder all the way through calculus and beyond, and be thinking about similarities and differences.
Alike and Different is another kind of similar routine. There's a great book out from NCTM called high yield routines that shares seven different structures Alike and Different as one of them that you can use for these kinds of talks. But at the time that book was written as a K through eight resource. So we really got thinking about what would it look like across secondary content? What would it look like beyond numbers? So for example, one of the routines is called today's number where students are given a number. So in the lower grades, it might be a number like 10. It's a really important number there.
The upper grades, it could be something like in geometry, 180. Really important number, right? Or square root of two or PI other numbers that are really important. But it can also be like today's expression where we give students an expression like on top of my head, 10X plus 25. And we ask students to represent that in as many different ways as possible to see what's coming up for kids. Our students thinking about different properties, like commutative property, associate property. Are they writing that expression in different ways?
Are they thinking about, "Oh, each of those parts has groups of five in it and maybe a rewriting it with distributive property"? Are they thinking about it visually and kind of like drawing a model? Are they thinking about, "Oh, that means like 10Xs. So like X, X, X, X, X, X, X. How are they actually thinking about these expressions? And what I would contend is that in my early teaching, my students weren't thinking about those expressions, right? I wasn't teaching them to be generative in mathematics and to think about these quantities in flexible ways, they would just think about that as like, "Oh, I guess that's an answer or the answer."
Kyle Pearce: Or what she's looking for, right?
Michelle Rinehart: Yes.
Kyle Pearce: Like what am I going to have to put on something at some point along the way here?
Michelle Rinehart: Right. Box That thing out, that's the right answer. So this was like a fundamental shift to have students think about quantities, not as what you're suggesting, this final answer, the thing we're looking for, but as like inherent mathematical quantities that we can do things with, that we can reason with and be flexible with. We might wonder like, well, why? Isn't it about getting the right answer, right? So why do all this like flexibility work, if it doesn't get you to the answer.
But what I've come to realize is that having that mathematical flexibility, empower students to be able to do other mathematics much more efficiently and with ownership and agency. So if you can think flexibly about quantities, then could you factor, could you look at equations differently? Could you do all of these things differently? So that's kind of a landscape we're trying to move into with Math Talks was to think about how do we develop those mathematical habits with secondary content?
Kyle Pearce: I love it. And thinking about that flexibility piece, I think as well, it's like shifting kids from this idea of like, "Oh, I don't know how to do that" to "I can figure this out. I'm not sure where to go right now, but I can work through this because I have the tools. I have the strategies that have emerged, the models that have emerged." I'm going to back up. You said in a roundabout way, what we've heard Cathy Fasano say as well, which is "Mental math, isn't math you do in your head, it's math you do with your head." I love that. It just so clearly helps us to realize that, "Wait a second. I was that teacher for so long where in math class, especially in grade 9, if I was working with students who have typically struggled in math, so they're in a stream, right?"
So now we're obviously talking about access and equity. We have a group of students who basically were underserved by the math education that they've had, overall. And now they've all been grouped into this particular class. And in my mind, I had the mindset of like, "I'm just going to show them how to do everything," like you said earlier, and I'm going to just make sure that they know how to use their calculator to help them get all the answers. And that actually worked for a long time with standardized testing, with what I was assessing and evaluating, like what I cared about at the time. That worked.
The problem was, is now when I look at the way I envision math and what I want for students that flexibility, it didn't work for that. Now, I want students doing more with their head. I want them to model, I want them to show, I want them to explain, to reason, prove, conjecture, all of those things. And it was totally missing early on. So I'm thinking back. And you had already mentioned, and you said it so well about this idea of how transformation happens slowly.
It's bit by bit. I'm wondering, so I think we'll focus in, in this math talk thing. I think it's really important for high school teachers to see the value, because I know when I go into a high school class, a lot of the Math Talks I do in high school classes are very similar to the Math Talks I'm doing with grade 5 grade 6 students. So if I'm in a grade 10 class and I'm using the same number strings as I'm using in grade 5 and 6, what does that tell you about how flexible our, I'm going to say, "traditional" approach of teaching math has worked for building their flexibility and their fluency. I'm going to say not so hot.
So my wonder is to the question after that long-winded five-minute conversation I just had with myself. I'm wondering, those are sitting at home and they're wondering, they're going, "Okay, this sounds amazing. We've heard Kyle and Jon talk about Math Talks before. Clearly, now Michelle's another person that's like advocating. How might you suggest someone who's listening, to get their feet wet to explore this idea?" Because like you said, the first thought you have in your head, especially in high school is, "Do I have the time to spend," or some might say, "waste on this if I'm not sure what the end goal or what the end result is going to be like?" Do you have any, like, get started tips that you might recommend they sort of point their attention to?
Michelle Rinehart: I think too, and you really laid this out, this idea of like, "Be clear on your goal." If your goal is to get students talking about mathematics to develop their mathematical flexibility, to be generative in their mathematical thinking, then where is that happening? And for me, I wanted all those things, but I wasn't doing things that would specifically build to that. So getting that clarity on why will really help you not just try something new, but stay with something new for the two to three weeks it takes for you to see success with it.
Because the first time you do anything new, both you and students are kind of like, "We're trying this out. We're not sure like this is a pushback on what we typically do in this class." So that's kind of like start with your why as a really important thing, I think as a first step. Once you're clear on your why, what do you want to come of this? And then that will help drive your follow through on it. But then what you're really looking for are specific examples of what would this look like at my grade level?
I think that's so incredibly important especially for secondary teachers is to see not just Number Talks, which are problems specifically about computation and with numbers, but in Math Talks, we move beyond that to think about what would a short routine look like that has students think about functions or think about, "I don't know comparing rational equations or some of the stuff that we get into in a high school math or in middle school math that goes well beyond just a computational problem." So as a starting place, I compiled a number of these examples of Math Talks across grade levels, on my website.
People can go to howweteach.com/mathtalks, and they will see examples from sixth grade all the way up through the higher level high school math courses of specifically what this looks like. What might be an Alike and Different that looks at, for example, rational functions or solving systems of equations, or other routines that look at geometry concepts, et cetera, just to kind of get a vision for what this could look like. Then grab some of those and try them with your kids in the first five minutes of class or in a five minute transition time in class a couple of days a week.
Again, think about your goal. If my goal is to get students talking about mathematics, thinking flexibly, et cetera, how might I begin to assess whether I'm seeing growth in that over a two week period? I really think that we will, and it really helps us see and believe what our students are capable of in terms of thinking and reasoning and communicating mathematically. But it helps students be empowered with that same thinking as well that there are things that I know that I can do. So those are two kind of first steps that come to mind.
Jon Orr: Yeah. Those are great actionable steps, and I really liked that. I think people need to hear more about goals and specifically addressing the goal you have in mind. I think a lot of teachers get bogged down or overwhelmed in the sense that, Oh, there's Math Talks. Oh, there's three-act math tasks or there's, which one doesn't belong, and there's all these things. I got to get into that." And instead of thinking first about what is the learning goal that I want to elicit with my students, and then maybe trying to find the right structure to help bring that out. I think you've provided some great, actionable tips, things that people can try without making a whole new change in their classroom.
That small wins is always something that is great for teachers to kind of get their feet wet like Kyle has used, and you've provided suggestions for. And again, thank you for providing your website. Everyone can go to howweteach.com/mathtalks to learn more about Math Talks. We're getting short on time, but I'm wondering what is, if you could think about one big learning goal right now that you would want our listeners to take away from this chat, what would you say would be something that one kind of big last message for them to walk away with?
Michelle Rinehart: I think one thing I'm thinking about earlier, you asked me like, what are some things thinking back to my chapter one, right? Another thing that I feel like I did not just in chapter one, but maybe all the way through like chapter five or six is that I was really thinking about empowering young women specifically in math. Right? I wanted young women to see themselves as mathematicians. I'm also specifically thinking about, "How I would empower my students of color to see themselves as mathematicians and to see themselves as capable and really to think about math or STEM fields as a next step."
But what I realized now is that while that was well-intentioned, I was really focused on empowering those students with content knowledge, right? If I teach them, if I help them learn really well, both either through this teaching by telling, which was my initial strategy. And then by teaching, by exploring, which is my secondary strategy. But I was really focused on like, if they can just learn the content, then there'll be set up well.
What I realized now is that there's this whole other kind of field of habits of mathematicians, if you will, that I wasn't explicitly fostering. So I think one of my big takeaways now would be to think about how we can, and I'm focusing in again on young women here, how we can help empower our female students to not be perfect in their math, but to instead be brave in their math, to be risk-takers in their math.
There's this incredible quote from Carol Dweck. I'm paraphrasing here. But if the world was just one big grade school, then women would rule the world. She's kind of calling out the difference between what is viewed as success in school. Right? Be perfect, be neat, follow all the rules, do all the things. And we train our young women to do that really well. And then that fails them when they get into these larger spaces of the real world, where which rewards bravery and risk-taking.
So I think this is particularly true in math as well where we've traditionally thought of math as a set of rules to learn and to follow and to mimic. So then what does it look like to empower our students as brave risk takers? So that's something I'm very much still thinking about and working towards and seeing that as a form of empowerment hand in hand with the content knowledge.
Kyle Pearce: I love that. That's a big takeaway. I feel like there's a lot of awesome, awesome thinking that people will take away from this conversation both around this idea of gender equity and bravery in mathematics versus just compliance. I think that's really, really a big piece. Then also this idea of flexibility and fluency. I think sometimes people and especially outside of education, there's sort of this idea of you use rote memorization to memorize math facts or you do all this other new math stuff and that there's this huge difference between the two when really what I'm hearing from you is like we want somewhere in the middle where students are flexible and fluent.
We want students to be confident when they want to calculate in mathematics, but at the same time we don't want them saying, "Oh, I don't know that one," and then shutting down. I'm getting that message from you as well. So I really want to thank you. On behalf of the Math Moment Maker community, it's been awesome to have you on, Michelle. It's been a long time coming. We were hoping to get you on much, much earlier time and, I don't know, PhD's get in the way and all of those things. So we want to thank you for taking some time out of your day having a chat here with both Jon and I and the rest of the community. We hope that we'll get to catch up with you sometime soon maybe this side of the border, once it opens.
Michelle Rinehart: Yes. That would be wonderful. Thank you all so much for having me on. It was such a pleasure.
Jon Orr: Awesome. Thanks for joining us.
Kyle Pearce: Hey, Jon, it was great to finally welcome Michelle on to the show. I know we had been talking about doing this for quite some time so it was great to get a chance to catch up and to hear about all of the great things that she's trying to do to bring to the math education forefront. Wow, awesome, awesome chat there.
Jon Orr: I always learn so much when we talk with math influencers just like Michelle. In order to ensure you don't miss out on our next episode as we release episodes every Monday morning, be sure to subscribe on Apple Podcasts or your favorite podcast platform.
Kyle Pearce: Also, if you're liking what you're hearing, do us a huge favor and share this podcast with a colleague and help us reach an even wider audience by leaving us a review on Apple Podcasts. Go ahead and tweet us @MakeMathMoments on Twitter or send us a message on Instagram or look us up on Facebook.
Jon Orr: Show notes and links to resources from this episode plus full transcripts can be found at makemathmoments.com/episode122. Again, that's makemathmoments.com/episode122.
Kyle Pearce: Well, my friends, until next time. I'm Kyle Pearce.
Jon Orr: And I'm Jon Orr.
Kyle Pearce: High fives for us.
Jon Orr: And high five for you.
Sign up to receive email updates
Enter your name and email address below and we'll send you periodic updates about the podcast.
DOWNLOAD THE MAKE MATH MOMENTS FROM A DISTANCE CHEAT SHEETS
Download the Cheat Sheets in PDF form so you can effectively run problem based lessons from a distance!
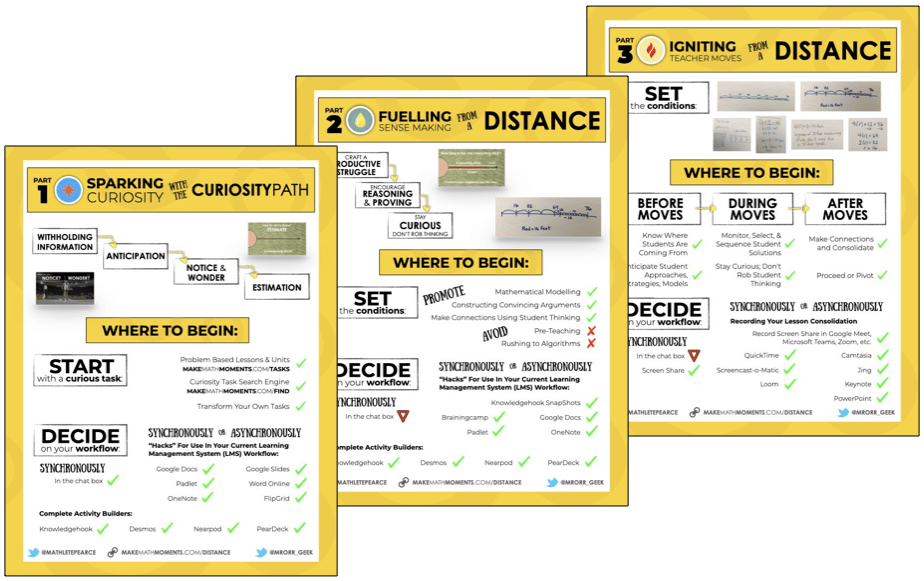
UP YOUR DISTANCE LEARNING GAME IN THE ACADEMY
There is a LOT to know, understand, and do to Make Math Moments From a Distance.
That’s why so many Math Moment Makers like YOU have joined the Academy for a month ON US!
You heard right: 30 days on us and you can cancel anytime. Dive into our distance learning course now…
Thanks For Listening
- Apply for a Math Mentoring Moment
- Leave a note in the comment section below.
- Share this show on Twitter, or Facebook.
To help out the show:
- Leave an honest review on iTunes. Your ratings and reviews really help and we read each one.
- Subscribe on iTunes, Google Play, and Spotify.
ONLINE WORKSHOP REGISTRATION
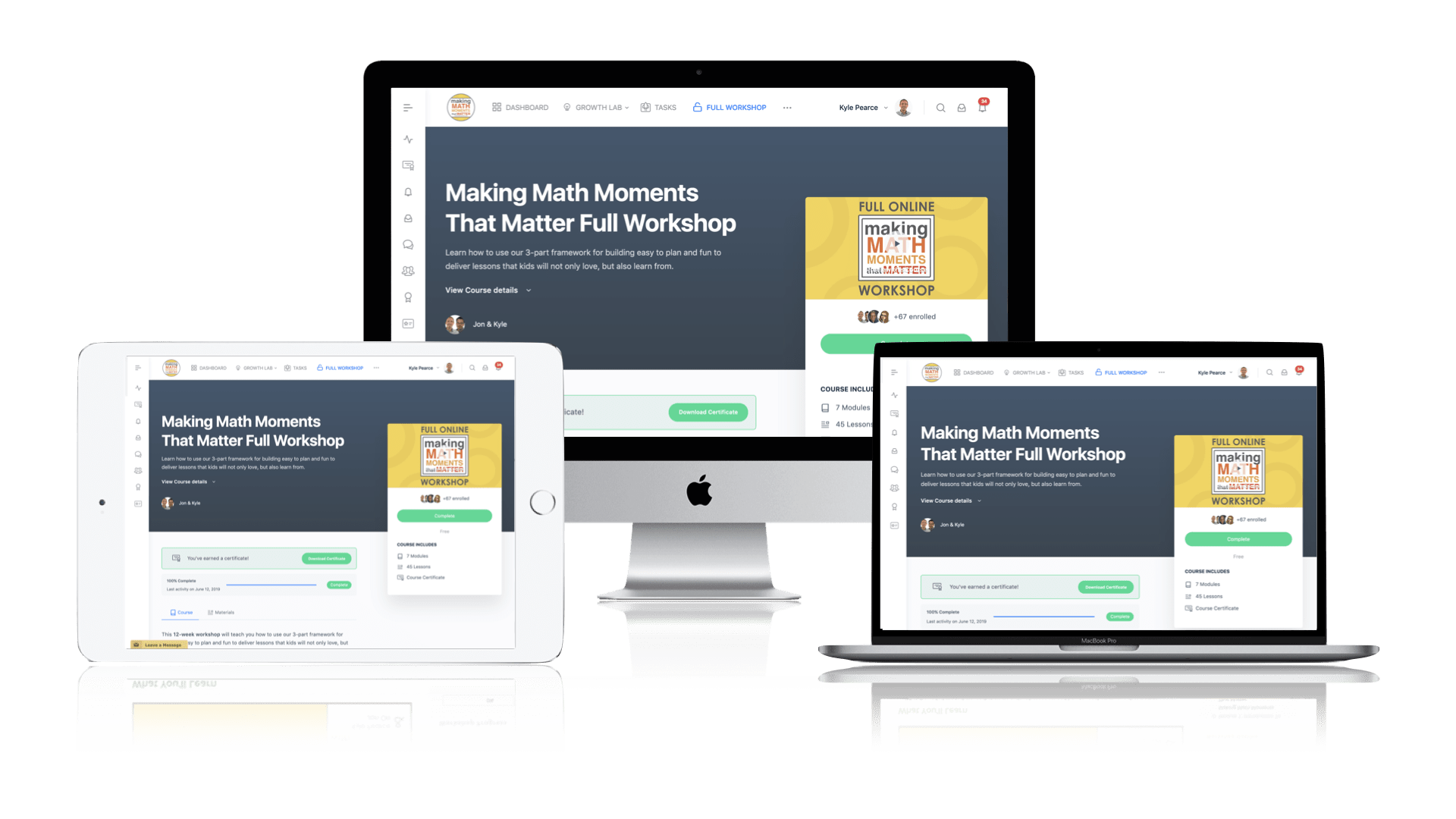
Pedagogically aligned for teachers of K through Grade 12 with content specific examples from Grades 3 through Grade 10.
In our self-paced, 12-week Online Workshop, you'll learn how to craft new and transform your current lessons to Spark Curiosity, Fuel Sense Making, and Ignite Your Teacher Moves to promote resilient problem solvers.


0 Comments