Episode #369: Avoiding The Trap of Algorithms in Math – An Interview with Pam Harris from Math Is Figureoutable
LISTEN NOW HERE…
WATCH NOW…
Are we teaching students fake math — and missing the chance to build real mathematical thinkers?
If you’ve ever felt frustrated that your students are following procedures without true understanding — or wondered why some students seem “mathy” while others struggle — this conversation with math is figureoutable’s Pam Harris will open your eyes. Together with Jon Orr, Pam Harris uncovers the hidden traps in traditional math teaching that reinforce shallow learning, and she shares how rethinking what mathing really means can transform both teachers and students.
By tuning into this episode, you’ll discover:
- Why many algorithms unintentionally trap students into rote learning rather than real reasoning.
- How to high dose essential mathematical patterns so that all students — not just a few — build deep, flexible thinking.
- Practical ways to shift professional development toward meaningful, lasting teacher growth (beyond just pedagogy tips).
Press play now to rethink what true math understanding looks like — and how you can spark it in every classroom – math is figureoutable!
Attention District Math Leaders:
Not sure what matters most when designing math improvement plans? Take this assessment and get a free customized report: https://makemathmoments.com/grow/
Ready to design your math improvement plan with guidance, support and using structure? Learn how to follow our 4 stage process. https://growyourmathprogram.com
Looking to supplement your curriculum with problem based lessons and units? Make Math Moments Problem Based Lessons & Units
Be Our Next Podcast Guest!
Join as an Interview Guest or on a Mentoring Moment Call

Apply to be a Featured Interview Guest
Book a Mentoring Moment Coaching Call
Are You an Official Math Moment Maker?

FULL TRANSCRIPT
Jon Orr:
Hey there, Pam, welcome back to the Making Math Moments That Matter podcast. I was just, you know, I was going down memory lane and I was looking at our past episodes and, you know, we’ve been doing this podcast for a while and some folks who are listening, know, been listening for some time when we first launched, I think back in 2018. You know, this is gonna be like episode 360 something, you we haven’t nailed it down exactly yet, but it’ll be in that range. We had you back in like, I think year two, you know, year two, was like episode 71. Which sounds like a long time ago, and I think it was a long time ago. And then we had you back on episode 255, which is itself like almost two years ago, two years ago. So welcome back. Hey, fill us in, give us a little update. You know, our listeners…
I think if you’ve been listening to the show, know who Pam is, but it’s also possible you know who Pam and then all of a sudden you showed up here. So fill us in, what’s going on in your world lately?
Pam Harris:
Yeah, John, I’m so grateful that you would have me back. Thank you. You guys are doing an amazing job. There’s only a few podcasts that are running as long as yours are, especially as consistent as you guys do. And so I’ll honor the fact that you’ve made it work. Yeah, look, I know what it takes. So yeah, so thanks for having me back. I do think I have a little bit of a new spin on some of the things that…
We’ve been doing some new things here at Math is Figureoutable and I’m super excited to kind of let people know. Yeah, I know that. One of the new things that I’ve been really thinking hard about and working with teachers in our coaching group and leaders in our coaching group is really helping people understand why the disconnect in math education and why it seems that we have maybe some math wars or some disagreements about extreme ways to teach and really thinking hard about helping people kind of understand different distortions that we’ve had about the nature of math and then what it means to teach math. And I’ve been putting that all in my brand new book, Developing Mathematical Reasoning, Avoiding the Trap of Algorithms. I think it’s a bit of a unique book study opportunity because it’s K-12.
Jon Orr:
That’s how it works.
Pam Harris:
I’ll tell you just as a little kind of interesting note, when I turned in the first draft, Corwin, so the publishers said, wow, like there’s a lot of math in this book. And I said, but yeah, you publish math education books. So, you know, of course you’re used to that. And they’re like, no, actually, usually we have books that are more about the how of teaching, which is super important. Like, let’s be clear. We need to talk about the how, the pedagogy, the teacher moves. That’s very important.
But would you consider that, I think in a lot of what we’ve done lately, we’ve kind of left out the what of mathematics. And that might sound like I’m, I don’t know, talking down to people, and I don’t mean to in any way, because in a big way, I’m addressing me, who was a very successful student and then high school math teacher, who then realized that my content was actually quite poor because…
I was doing what I now call fake math and I wasn’t really math-ing at all. And so I’m really thinking hard about ways of helping people kind of understand what I mean when I say that we might have some distortions about the nature of math. And one of the stories that I’m kind of excited about, it seems to resonate with people, I played basketball. So I don’t know you’re watching the podcast, you’ll notice that I actually have a basketball in my background. It was kind of a…
Big part of my life. I played internationally in Switzerland. It was super fun. But as I was learning to play basketball, I could not figure out how to do a layup. So you know, layup is that cool thing where you like dribble dribble student and goes up. Yeah, layup, you you look really cool. If you’re taller than me, then you dunk the ball at the end. But when I was learning to play, just physically somehow I just couldn’t kind of get it right. I needed…
Higher doses of helping me figure out what a layup meant. But as I was learning to do a layup, my coaches put me in games. Like I was allowed to play the real game of basketball. I could dribble, I could shoot, I was pretty good at defense. And so they put me in games and I could play even though I couldn’t do that. That one part didn’t make sense to me.
The system was set up to allow me to use what I did know and what I could do while I played the real game of basketball. I wonder if we’d consider that for some reasons, and I’d love to talk about them, our system has been set up to say to kids, if you don’t kind of naturally see through the algorithm to make all these mathematical connections, we’re not sure why, but we’re gonna put you kind of in this fake game of math, and we’re gonna have you just…
Like practice that algorithm some more and hope that if you just kind of keep doing those steps, then maybe you’ll magically kind of get the stuff that the rest of us sort of naturally picked up. And we’re not sure why, but we’re going to kind of put you in this fake game of math. And that’s a little bit of a tricky thing to say because people are like, what do you mean? Like fake. I’m not calling people fake to be really clear at all. I think the system has been set up…
To say to students, yeah, we’re not sure why you’re not naturally picking up on place value or reasonableness or the sense of magnitude of numbers or how these structures fit together. So we’re just gonna put you over here and just kind of have you keep repeating stuff that’s really not working for you, but we’re not sure why. And maybe if you put some grit into it and really just kind of trying to rote memorize that stuff, it’ll magically happen. Or I guess you don’t have the math gene. I’m suggesting we can beat that.
We can actually help teachers and students math the way mathy people actually math. And I got to be careful there because John, as I look at you, I’m like really aware as I say mathy people, people might like push back on that. Are you saying there’s a math gene and some people are mathy and some people aren’t? You know, I kind of am saying that there’s careful, careful here, hear me out, hear me out. That there were colleagues of mine, students, friends of mine who were…
More naturally inclined to do a layup. Like they did it the first couple times somebody showed it. Maybe nobody even had to teach him how to do a layup. They just kind of picked it up. Maybe that was you. I can picture you.
Jon Orr:
Yeah. Well, I was just going to say like what I would argue there, because I’ve had lots of thoughts around this as well. And we should talk about the creating math epiphanies is an essential component of what we’re trying to do in our math class. But in a way, it’s like when you think of those like mathy people the way you’re trying to describe them right now, like when people pick up things, one of the things that we’ve been chatting a lot about is like this pattern recognition. Like some people have built pattern recognition quicker than others…
Just through repeated reinforcement of pattern recognition in all aspects of their life. And then when they get into math class and we teach it in a pattern recognition way, which means when I see a problem presented this way and I see these key numbers in this format, then I can apply blank algorithm. Those tend to be folks like you and me who were successful in math and we had early pattern recognition success. And then we can apply that pattern recognition to being successful at math because for me…
Pam Harris:
Yeah, at least what we thought math was. Yeah.
Jon Orr:
Like you, was, that was all it was to me. It was, it was basically going like, Hey, I can see this format and I apply this thing in that format and I can just repeat that. And, and when I can, I can see it quickly and then make those connections quickly. Then I’m good at math, but really we were like, what you’re suggesting is like, we’re not really mathing. We’re just pattern recognition. So that’s in a way like tie that back to the math wars, right? Like what is…
What is math? Like, are we doing when we are doing math? Are we supposed to be like just pattern recognition and that’s what math is? And then therefore applying, say, already created, you know, scripts? Or are we actually thinking about this problem in problem solving? Because I think that’s what actually like is this, hey, I’m teaching procedurally in math facts, or I’m letting kids, you know, use the inquiry process to learn through this way.
And that’s where that pendulum swings back and forth, right? Because it’s like our fundamental beliefs are different about what we’re trying to do in our math class.
Pam Harris:
Well, beliefs is tricky because it depends on our background and the perspective that we sort of had. Would you consider maybe me using a bit of what you just said with pattern recognition? What if, I don’t want to tear you apart, I actually want to use what you said. What if the pattern recognition, what if we took advantage and helped kids get better at the more mathy pattern recognition?
Jon Orr:
Of course, go to it. Tear me apart, I love it.
Pam Harris:
What if we high dosed kids with patterns like place value? And I say that and I’m aware of how people hear what I say. What if we high dose them with the same patterns that I think naturally mathy people sort of picked up on? For example, I think when I listen to my young son, he would say to me, you know, mom, I don’t like to take naps in kindergarten. But what I was doing when I was laying there and forced to lay there on that mat and I wasn’t going to sleep…
My teacher had these dot patterns up on the wall and I would play with those dot patterns and I would, I realized that if I put certain ones together, they would create other ones. That kind of pattern recognition is actually super helpful because what he was doing was noticing the makeup of numbers. And when he began to notice that he could make tens out of different partners of numbers, then all of a sudden he had created partners of 10.
Well, that pattern recognition is super helpful, much more helpful than, like you said, what you and I were doing, which was realizing which rule to apply and then kind of having a pattern of a rule. He was actually doing what I would submit. Would you consider that? Think mathematicians in history went about the same world that everyone else went about. And as they went about their world, they ran into certain mathematical patterns and…
They were able to take that low dose that everybody was running into. And for whatever reason, they took that low dose and created mathematical connections in their heads that then when they ran into other patterns, they could add to those neural connections and make stronger and deeper and more dense connections. And then they kept playing with those connections. And because they owned these real math connections, not just patterns to apply which algorithm when, algorithms weren’t created maybe then at that point…
They were able to math, that that’s the way mathematicians actually math. The good news is we now know what those patterns, those important patterns are, and we can now high dose kids with those patterns. We can take kids like you and me, we’ll call us kids, we’re young, right? Look how energetic we are. We can take kids like you and me and we can high dose us with those patterns, and then we can realize…
Kind of like you said, I can inquire, I can look at a problem and I can say to myself, what do I know? What patterns have I recognized in the past that I could bring to bear here? Not what can I wrote, memorize and mimic, but what relationships and numbers and structure have I created that now I can use to reason logically through this problem? And that’s mathing. And then we’re all mathy people. I wanted to make sure I got that in here because I had I kind of said mathy people and naturally mathy people. Got to make sure I define.
Jon Orr:
Yeah, no, I completely agree. Like completely agree. It’s about emphasizing what patterns are we actually trying to help our students understand and how to use those patterns, right? So it’s like, that’s the important component that I think for a long time, you and I, when we first started teaching, skipped over. We focused on the wrong, in a way, the wrong patterns. Yep, no, not on purpose.
Let’s kind of keep unpacking this and how it relates to some of the work that you’re doing to help address this issue, thinking about, because you mentioned how to help teachers. And I think we agree that our best foot forward to help our students understand what we’re trying to do in our math classes and make sure that they understand math at that conceptual level, that deep level, and be able to be flexible, fluent, all of those things that I think we all…
Think about when the people who are listening to this podcast think about when we think about math class. You know, how best are we helping? Like, what are your recommendations right now? Like, we know helping teachers with those math epiphanies, those math understandings is kind of our best foot forward so that it can transfer in the classroom. What do you say recommending now? Like, what does that look like when we’re helping a teacher unpack…
Pam Harris:
Maybe a couple of things. I’m going to emphasize that if you ever do anything with me, you see me in a session, you’re in our coaching group, you’re in one of my online workshops, you’ll notice that very right off the bat before I do kind of any hardly talking at all, I’m going to immerse you in a mathing experience. And so we’re going to do probably a problem string where I’m going to attempt to get teachers to do either what they’ve kind of already naturally done, but never seen anybody do…
Structurally, strategically, purposefully with a purpose with students. Like they’ve always kind of said, well, you know, if you show kids the steps of the algorithm, then they’ll see these things through it. And I’ll say, why do you think that? And they’ll say, well, because I did. And I’ll go, well, I didn’t. Are there other experiences? So if you’re that person, when I do that math experience, you may already own those mental connections. You’ve already been math-ing that way. But maybe for the first time, you’re seeing a way…
To help students do what you kind of naturally did. That’s a big epiphany for teachers. They can say, whoa, this is a chance for me to actually help my students do what I kind of did without that help, but I can help more students do that. So that’s one kind of group. Then there’s the teachers more like you and me as they’re immersed in that mathing experience. John, it’s interesting. I’ve gotten really good lately, or at least I focus on trying to do this lately, where there’s a moment in that mathing experience, there’s a problem in the problem string…
Where I’ll say, what do think about this one? So we’ve done a few problems, I’ve modeled thinking, it visible, we’ve kind of compared some things. And then I’ll say, well, how about this problem? How are you thinking about that? And then I’ll look out at the group and I’ll watch their eyes and I’ll notice that they’re kind of doing, if you can see me physically, they’re kind of doing this like, okay, like it’s almost like they’re on the balls of their feet and they’re looking forward and you can see that they’re kind of energized and they’re looking at what we’ve already got on the board or on the screen and they’re going…
Okay, like how can I use that logically reason? And in that moment I go, stop, pause. Everybody take a picture of your brain. Did you right now feel in your brain that you just reached in rote memory and you’re gonna mimic something you’ve seen before? And they all go, no. And I go, did, what were you just thinking? What were you feeling? What was your brain doing? And they go, well, I was, like, were you looking? Did you, did you just like…
How can I use? Was it almost game-like? Were you trying to be like, ooh, how can I be clever? And like, is there a way that I get that, that, that, that right there? That thing you were just, that mental action? Those are the mental actions of a mathematician. You were math-ing. I’ll thank Dr. Deborah Creighton for bringing us the math-ing word. I think that’s been super helpful in my work to talk about the act of doing math as math-ing, not as rote memorizing and mimicking.
That’s what maybe we’ve kind of been fed was the thing. The system has been set up to pretend that’s what math thing was. But man, we can actually do the mental actions that mathematicians do. I think, John, think teachers have to have, so it’s only the first step, but I think they have to have that experience of going, wait, that’s what you mean by inquiry? I thought this whole time when you were talking about inquiry that I was supposed to just have kids kind of wander off on their own. And I was supposed to say…
Hope you figure out math on your own. Good luck and come back when you got it. And it wasn’t structured. It wasn’t, we didn’t have real helpful ways of helping kids progress and scaffold. We didn’t have even really clear goals because you might, if you’ve kind of heard inquiry or discovery as being like this free for all and your kids are just kind of on their own, you might’ve thought that they were supposed to invent the algorithms. Not so…
Not so at all. Can I just share a brief experience that happened recently? I was at a conference and I was in a session and they said, turn to the person next to you, just meet him really quickly. So I said, random person that she doesn’t know me, I don’t know her. Hi, how you doing? And she said, yeah, this discovery crap is terrible. And I said, oh, tell me more about that. Because again, if you describe discovery kind of the way I just did, then you do think it’s garbage.
And I’m kind of agreeing with you if it’s just leaving kids on their own to struggle unproductively and we don’t really know ways to help scaffold them. Anyway, she said, she goes, yeah, this is terrible. And I said, tell me more about that. And she goes, yeah, I tried it. And I said, what did that look like? And she said, I went to my eighth grade kids and I said, all right, today, today you’re going to discover the Pythagorean theorem, go. And then she paused and she goes, do you think it worked? No.
So as soon as you know it didn’t work, then I was like, come back here. I’m going to teach you the Thagarin theorem. So I chuckled a little bit inside. I was like, well, I agree with you. That’s not going to work. So then what do we mean? And I think that’s not a trivial question. And I don’t think it’s a one-time shot. I know I’ve heard you and Kyle talk about how it’s long-term, sustained professional learning. We’re all on a journey. And in that journey, we need follow-up support. We need to be able to come back and go, OK…
Like I believe you that we can reason through these kinds of problems. How do you reason through those kinds of problems? Like I’ve kind of got these linear function thing down, but I don’t know how to think about exponential functions. Where do I even, I’m not reasoning. Like, that’s when we as adults feel like we have the safety and the security to go, okay, like I’m now reasoning with this kind of math, but help me reason with that kind of math. Like I don’t even know where to start. I’m not, you know, when we recognize…
I’m not reasoning with that kind of math. How can we reach out? Kind of… And I love the fact that you’re creating a community, I’m trying to create a community where we’re helping each other really think about, how are you thinking about that? Hey, mathy… It’s one of the pieces of work that I’ve been doing for last 20 years is interviewing people, interviewing mathy people, interviewing people who were not mathy yet, who are becoming mathy and asking people, how do you think about this?
And then really getting under, if that’s how mathematicians reason about that thing, ooh, how can I scaffold? What kinds of experiences can I high dose kids with? How can I high dose them with the kind of low dose patterns that those mathematicians were able to use? Let’s high dose them with those patterns. Bam, now we’ve got kids math-ing, well, teachers first and then kids math-ing, mathematicians actually math.
Jon Orr:
So what I’m hearing is that we need to do, when we think about professional development, too often we’ve been focusing on the moves, pedagogy, but not the math, not getting our teachers to do more math with each other, with themselves, and feel comfortable with strategies and maybe the models, and getting that brain working in that way so that they can then transfer that experience to their students and start crafting or adjusting or modifying their existing lessons to give those same experiences to their students.
Do you feel like it looks, like does the PD support or the message or even it look different between elementary, like K to eight versus nine to 12? Like, do you feel like there’s a difference there? Is there an emphasis difference? Like, I know you being a high school teacher, me being a high school teacher, you we had lots of success in our own classrooms…
Pam Harris:
Fundamentally, no, but there is definitely a, what’s the word I want to say? Attack sounds too like I’m going to fight, but the way that I approach, say a teacher who went into teaching because they love kids and they want to teach, and it’s not so much that they were really interested in math, but yeah, they’ll teach math, it’s fine, but I love kids and I want to teach. That personality…
It’s not the right way to say it. That mindset is a bit easier to say, hey, let’s do some math. Let’s maybe learn some things about math because they kind of recognize. They don’t claim to be a mathematics expert. It’s not part of their identity that they’re, yeah, I’ll just say that. So they’re a bit more willing to kind of dive in and learn some stuff without maybe some baggage that…
Perhaps a high school teacher or even a middle school teacher or maybe even a younger grade teacher who went into it saying, I am good at math. And I know a lot of high school math teachers and I blame them for this. I was this way. I thought I needed to know all the math. I had to be the god of math in order to not be an imposter as a high school math teacher. So man, you asked me a question. I knew the right formula. I knew the right algorithm. I recognize that question…
And if I didn’t, I could do it. I could derive it. Could figure that out. No problem. I knew the math. I wonder if we can help. Golly, how do I say it? Is it possible that when we say to somebody who went into the mathematics teaching profession, believing that they were good at math, when in reality maybe they were good at fake math, that’s a tricky place to be?
It was a tricky place for me. Imagine my, I’ll just say it clearly, midlife crisis, when as a very successful, I’m putting that in quotes, high school math teacher, I realized that wasn’t math thing at all. It was rote memorizing and mimicking. Like I had to figure out what that meant for me as a high school math teacher. And how do I deal with kind of that, I don’t know, disequilibrium of like, there’s maybe things…
That I don’t know. Now, the brilliant part was for me, I had a lot of wonderful mentors who kind of quickly helped me go, it’s okay that you’re there. We’re all on this journey. Dive in and we’ll learn with you. That’s the kind of message I try to send in PD. Let’s dive in and learn together. But I’m very careful with high school teachers to honor the fact they’ve worked hard. They do know a lot. We’re to take advantage of what they do know…
And I’m not going to attack. I’m not going to tell them right off the bat, you’re terrible for being, now like it was me. Or maybe you’re, you might be listening to the podcast going, it wasn’t me at all. I’ve always been math-ing. Fantastic. I’m a little jealous of you. Yeah. The good news is I can help you help students do what you kind of naturally did. That’s the great news. And maybe you’re already doing a superb job of it. We can probably tweak that. I can maybe help you tweak that a little bit because I’ve had a lot of experience of working with…
A lot of different teachers and lot of different experts in pedagogy and brain science and bringing it all together to kind of help in specific areas of math. Maybe we can all help each other.
Jon Orr:
Right. You know, like those are definitely great points because it’s like, those teachers do have a lot of understanding around math. And I used to argue like yourself is that I had that very procedural understanding and I couldn’t be stumped in terms of say any sort of math problem, but I always learned it the one way and I could teach it the one way. And then I tried to like figure out how do I say it differently? And usually it was louder and slower, you know? And, but I think there’s a lot of power in supporting teachers by…
By trying to help them grapple with what they know about their say, say algorithmic thinking or approach and understanding of say key concepts and then having them see it represented differently in different patterns, in different models, in different strategies. Like if I look at say a different type of factoring that is like, know, sometimes you see these tricks online in YouTube and all of a sudden it’s like, that’s a weird way to factor. But then it’s like, how do you see like what you do for factoring is similar to what…
That is for factoring, like trying to like create these epiphanies of like, how do you see like, like if we’re are going to kind of start going down the area model as a, as a, as a vertical model that we could stretch across grade levels, like how are you seeing your current understanding of, you know, using the distributor property or working with the distributor, the distributor being flexible with it in this version, like how, how can you represent it visually? How can you represent it in different ways? Like there’s a lot of power in helping those…
Pam Harris:
I was gonna say connections in a big way, connections between different types of functions, connections between representations. Often teachers will say, you’re about multiple representations. And I’ll say, I’m about connections between multiple representations and multiple functions and transformations and what’s, and then coming up with generalizations. Hey, if I can mention one other thing, you kind of asked me like if there was a difference and I sort of said fundamentally no, but here’s a thing, know, like…
In my new book, Developing Mathematical Reasoning, Avoiding the Trap of Algorithms, I actually take a systematic approach to K-12 math, which I think is very unique to have a book that says, let’s take a look at a few key algorithms and point out some major ways that they can trap students into using less sophisticated reasoning than those problems could be developing.
And if we trap kids into using less sophisticated reasoning, then the problem could be developing. Now, then when we try to build on that to the next sort of hierarchical, the problems that would use the kind of reasoning we could have been building, but we weren’t because we were trapped in less sophisticated reasoning, now kids can’t actually progress. So in I think a very unique way, I took a look at some major algorithms along the K-12 spectrum and said…
Hey, here are some ways that those algorithms can actually trap kids into looking successful, but actually they’re using less sophisticated reason than it could be. Or it traps kids into thinking, gee, I can’t do that very well. I guess I’m not a math person because I can’t rote memorize and mimic and tell the difference between that algorithm and this one or what the steps are, which one I should apply when.
Gee, guess I’m not a math person. So those are two of the major traps. And a third major trap with all of the algorithms I’ve looked at is the algorithms are amazing historic achievements. In part, because they put a lot of place value and meaning and structure kind of behind the scenes. They’re very opaque. They’re hard to see through. They’re hard to kind of, now some people do, many people listening to the podcast might be like…
I can totally see all the stuff behind the algorithm. Well, good for you. A thing to know is many, if not most of us can’t do that, won’t do that. And so it can trap us into kind of a digit approach or a take apart piece approach. So instead of looking at all the numbers when we’re solving a problem, we look at the digits in the numbers and we just do stuff with digits. Well, Pam, that makes it easier. Sure. But it also takes away the magnitudes…
We don’t ever have kids deal with the sense of size and how they relate to each other. And then we say to kids, guy, your answer’s completely unreasonable. But we took them out of reasoning land to begin with. So I can’t assume that there’s these three major traps with all of the algorithms that are out there. One, it can trap kids into using less sophisticated reasoning than the problems were intended to develop, could be developing. Two, it traps kids into this sort of digit or piecewise…
Sense of the problems so they never actually deal with what’s actually happening in the problems, the magnitudes and the structures. And three, either it works on our identity in mathematics. Either we kind of rote memorize and mimic well and then like you and me get this false sense that we’re good at mathematics or we can’t do that well or it’s not, let me be clear, I think there’s a lot of students out there that aren’t interested in rote memorizing and mimicking.
They look at that and they’re like, when am I ever going to use this? Well, if you hear that, I invite you to consider that what you’ve done with kids is more on the side of parsing things out into digit oriented stuff, getting them to think that math is just rote memorizing and mimicking. And that’s not interesting for many kids. And they just refuse. They’re like, I’m not playing that dumb game. I got better things to spend my mental energy on. And then that is sort of this identity trap. There’s only three of the major traps that I identified. But I think they hit them all, all the algorithms.
Jon Orr:
Yeah. Well, yeah. Yeah, no, and I think that’s a big, takeaway from, you know, your, your new book and being a K to 12 book and really unpacking, you know, that being, Hey, this is an important, important takeaway of under, under, under discovery, you know, understanding the algorithms and the trap that we’re falling into when we think about them. I know, I know folks can go learn more about the work that you’re doing at mathisfigureoutable.com. You have a podcast, it’s on all…
Podcast platforms. Know many of our listeners listen to your podcast as well. Where else, Pam, can people reach out to you to kind of keep digging in and learn more?
Pam Harris:
We also have a Math is Figureoutable teacher group, teacher Facebook, some meta, I’m super active on social media, so if you follow me there, you can see that we put out a ton of free stuff all the time. A companion to the Developing Mathematical Reasoning, Avoiding the Trap of Algorithms, we have a free workshop called Developing Mathematical Reasoning that’s out there. You can check that out on, again, mathisfigureoutable.com. We also have an instructional routines hub…
On mathisfigureoutable.com where you can go check out examples of problem strings and other really cool routines can really help you math with your students. I’ll mention that along with the K-12 book that’s just been released, and can I just say, I’m super excited, we hit the best seller on Amazon in mathematics education. Yeah, I’m thrilled. Thank you everybody for supporting. It’s kind of a unique opportunity for districts to do a book study…
Because A, it’s K-12, there’s math in it to discuss. And in such a way that teachers of young students can be having conversations with teachers of older students in a very unique sort of district-wide or book study-wide way. But coming soon will also be the companion books, K-2, 3-5, 6-8, 9-12, that can help continue that book study idea where…
We sort of identify the traps of algorithms and a lot of really good things to do in the anchor book. But then we really dive in and what are the major strategies and models to develop in those grade bands and how to do it in those grade band books that will be coming out shortly. So just let everybody know that that’s another way, another way to learn more.
Jon Orr:
Awesome, awesome. Hey folks, mathisfigureoutable.com, head over there. The link will be in the show notes, but I’m sure you know how to get there on your web browser. So head there, lots of resources for you to dig into. Pam, this has always been a pleasure, I guess it’s been a pleasure as always, and let’s do this again real soon.
Pam Harris:
Awesome, John. Thanks so much and great work you guys are doing as well. Sure appreciate the movement you’re helping everybody make. Take care.
Jon Orr:
Take care.
Thanks For Listening
- Book a Math Mentoring Moment
- Apply to be a Featured Interview Guest
- Leave a note in the comment section below.
- Share this show on Twitter, or Facebook.
To help out the show:
- Leave an honest review on iTunes. Your ratings and reviews really help and we read each one.
- Subscribe on iTunes, Google Play, and Spotify.
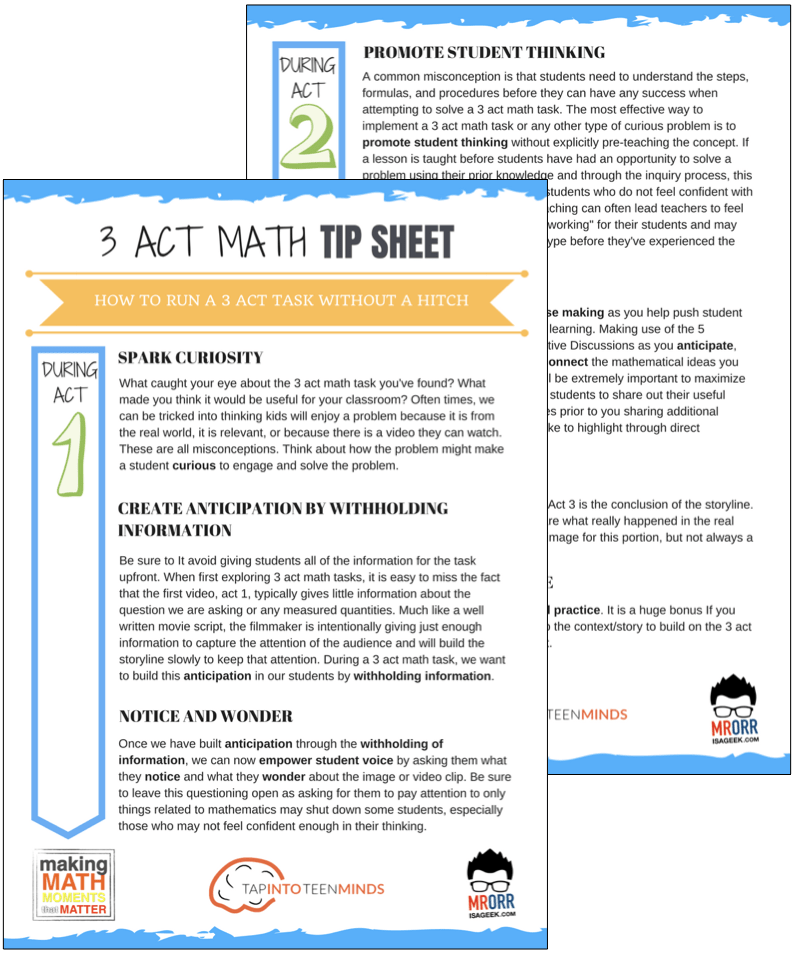
DOWNLOAD THE 3 ACT MATH TASK TIP SHEET SO THEY RUN WITHOUT A HITCH!
Download the 2-page printable 3 Act Math Tip Sheet to ensure that you have the best start to your journey using 3 Act math Tasks to spark curiosity and fuel sense making in your math classroom!
LESSONS TO MAKE MATH MOMENTS
Each lesson consists of:
Each Make Math Moments Problem Based Lesson consists of a Teacher Guide to lead you step-by-step through the planning process to ensure your lesson runs without a hitch!
Each Teacher Guide consists of:
- Intentionality of the lesson;
- A step-by-step walk through of each phase of the lesson;
- Visuals, animations, and videos unpacking big ideas, strategies, and models we intend to emerge during the lesson;
- Sample student approaches to assist in anticipating what your students might do;
- Resources and downloads including Keynote, Powerpoint, Media Files, and Teacher Guide printable PDF; and,
- Much more!
Each Make Math Moments Problem Based Lesson begins with a story, visual, video, or other method to Spark Curiosity through context.
Students will often Notice and Wonder before making an estimate to draw them in and invest in the problem.
After student voice has been heard and acknowledged, we will set students off on a Productive Struggle via a prompt related to the Spark context.
These prompts are given each lesson with the following conditions:
- No calculators are to be used; and,
- Students are to focus on how they can convince their math community that their solution is valid.
Students are left to engage in a productive struggle as the facilitator circulates to observe and engage in conversation as a means of assessing formatively.
The facilitator is instructed through the Teacher Guide on what specific strategies and models could be used to make connections and consolidate the learning from the lesson.
Often times, animations and walk through videos are provided in the Teacher Guide to assist with planning and delivering the consolidation.
A review image, video, or animation is provided as a conclusion to the task from the lesson.
While this might feel like a natural ending to the context students have been exploring, it is just the beginning as we look to leverage this context via extensions and additional lessons to dig deeper.
At the end of each lesson, consolidation prompts and/or extensions are crafted for students to purposefully practice and demonstrate their current understanding.
Facilitators are encouraged to collect these consolidation prompts as a means to engage in the assessment process and inform next moves for instruction.
In multi-day units of study, Math Talks are crafted to help build on the thinking from the previous day and build towards the next step in the developmental progression of the concept(s) we are exploring.
Each Math Talk is constructed as a string of related problems that build with intentionality to emerge specific big ideas, strategies, and mathematical models.
Make Math Moments Problem Based Lessons and Day 1 Teacher Guides are openly available for you to leverage and use with your students without becoming a Make Math Moments Academy Member.
Use our OPEN ACCESS multi-day problem based units!
Make Math Moments Problem Based Lessons and Day 1 Teacher Guides are openly available for you to leverage and use with your students without becoming a Make Math Moments Academy Member.
Partitive Division Resulting in a Fraction
Equivalence and Algebraic Substitution
Represent Categorical Data & Explore Mean
Downloadable resources including blackline masters, handouts, printable Tips Sheets, slide shows, and media files do require a Make Math Moments Academy Membership.
ONLINE WORKSHOP REGISTRATION

Pedagogically aligned for teachers of K through Grade 12 with content specific examples from Grades 3 through Grade 10.
In our self-paced, 12-week Online Workshop, you'll learn how to craft new and transform your current lessons to Spark Curiosity, Fuel Sense Making, and Ignite Your Teacher Moves to promote resilient problem solvers.










0 Comments