Episode 156: Why Use Math Talks and How To Ensure They Are Effective
LISTEN NOW…
WATCH NOW…
Math Talks, Number Talks, Minilessons, Warm-ups… What are these routines? Is there a difference? If so, what are those differences?
In this episode, we’ll unpack what we believe the true elements of a Math Talk are and how you can leverage the power of an effective Math Talk in your classroom to start your next math lesson!
You’ll Learn
- What is a math talk and what Is not a math talk;
- The Teacher Moves necessary to lead a math talk effectively;
- Why you should include math talks into your programming; and,
- What resources exist so I can start tomorrow.
Resources

FULL TRANSCRIPT
Kyle Pearce: Hey, hey, Math Moment makers. Today, we are going to be diving into this little thing called math talks. Some of you might call them number talks or mini lessons or warmups. Today, we're going to talk a little bit more about these routines. We're going to talk about whether there's a difference between a number talk and a math talk, or a warm up, or a mini lesson. And if so, what are those differences? We're going to unpack those here with you today.
Jon Orr: Yeah, in this episode, we're going to unpack those and what we believe to be the true elements of a math talk and how you can leverage the power of an effective math talk in your classroom on your next lesson.
Kyle Pearce: All right, before we dig in my friends, Ali, cue up our music. Welcome to the Making Math Moments That Matter Podcast. I'm Kyle Pearce.
Jon Orr: And I'm Jon Orr, and we are from makemathmoments.com. We are two math teachers who together ...
Kyle Pearce: With you, the community of Math Moment Makers worldwide, who want to build and deliver problem-based math lessons, that spark curiosity.
Jon Orr: Fuel sense making.
Kyle Pearce: And ignite your teacher moves. Yes, my friends, as we mentioned in the intro, we're going to be taking a dive today into this idea of math talks. Many of you who are listening have probably heard of math talks, or number talks, or warm up routines, there's all kinds of different terminology. But today we're going to try to dig in there a little bit more deeply, and we're going to try to comb through some of the nuances because I'll be honest and say, I thought I was doing math talks for many years and the way I'm doing them now is very different than the way I was doing them five years ago or even eight years ago. So, we're really excited to dive in there, Jon.
Jon Orr: This conversation, I'm excited for, because I'm curious to see many listeners who have listened to many episodes, know that we don't teach in the same district. We just met online and we communicated and built a good rapport between us and we share our ideas back and forth and been doing that for years and years. So, I'm actually curious to see what you think a math talk is versus a number talk and warmup routines versus what I'm doing because I know that you're spending a lot of time in the elementary, middle school land and I'm a high school teacher, whereas you're a consultant. So, I'm curious to see what you've been doing. I'm going to compare, I think, with what I've been doing with math talks in my classes. So Kyle, what are you seeing in math talk? And why should we talk about this today?
Kyle Pearce: Actually, I thought when we hopped online, I said, "It'd be great to actually have this discussion," because just to go to my day, reflecting on my day today, had an opportunity to go into one of our elementary schools, one of our K through grade eight schools. I got to go into, I think it was six different classes throughout the day, and basically got to do some Minilessons, which is a resource, we'll talk about that resource shortly, but it really involves sort of a type of math talk. A lot of educators want to get a sense as to what it looks like and sounds like in action.
In my district, we had been leveraging a book called Number Talks by Sherry Parrish. I think that was, at least in our district, and I think in your district probably be pretty similar for the elementary teachers, that resource was sort of the, we'll call it like the math talk bible for quite some time.
Jon Orr: That's what I was thinking.
Kyle Pearce: It was almost like that is what a number talk is. And maybe some of you listening are using that tool as well, and what a great tool to get us thinking about the importance of number sense and really kind of bringing back some of these, dare I say it, basics to the table, but not doing so just through rote, but doing so through this routine.
For me and in my district, we've actually been exposed to some other resources as well, so we'll unpack some of those here today and we just want to comb through some of the nuance. Jon, when you started doing math talks, I think you and I were doing them in a similar way. It wasn't with the Sherry Parrish resource, but for us, I think it was using internet websites, right?
Jon Orr: Yeah. That's when somebody back a few years ago would say math talk, even numbers talk back then was, I was equating it to warmups. I think it was like, let's start class with a minds on activity, a warm up, an activity that gets us thinking about number sense. So for me, this was like, which one doesn't belong. We would put the image of the ... could be numbers, and we'd say, "Well, which one of these doesn't belong with the rest?" And kids would think-pair-share with their reasoning. That was a great resource, I use that. I still use that to this day for warmups.
Then there's Estimation 180. There's also, Would You Rather Math? From John Stevens. These were all these internet blog websites that put a ton of resources to get your students engaged, talking about math and also justifying some reasoning. Every one of those was about a justification. These are great resources, so I was equating math talks back then with these warm up activities, Kyle. That's not what you were referring to right here, right?
Kyle Pearce: Yeah. I'm going to take it a step further and I would say ... and something I want to preface with too is up on my screen here if you're watching on YouTube, you'll see that we've got which one doesn't belong up here. We have Estimation 180. We have, would you rather, there's Math Is Visual. There's all kinds of different resources, which are great. I would argue that they are a form of math talk, they definitely are because it does get students talking.
For me, I think one of the biggest benefits that I noticed by using these websites was actually shifting from this sort of sit and get lecture style that I was using in my math class. It helped me over time, gradually get students doing more of the talk and getting it to be more of a debate, more of a discussion. So, I think these are great tools to do that.
Some of the things that we've discussed as well though, is I found that now I try to build in some of these types of routines into all of our lessons, for example, Estimation 180, we try to build in estimating into every single one of our problem-based lessons. So, I didn't need to use Estimation 180 as much anymore because we were building that into our problem-based lessons.
Something that I noticed teachers in my district were doing for quite some time when they were using the Number Talk resource was there was a really, I would say maybe even an over-emphasis on students doing all of the work in their head, so it was like mental math and that's great work. It's really helpful but what I found is that if students weren't there yet, there was a group of students that weren't maybe at the same place as the rest of the students, we would still have this disparity. Some students would be left behind. I was thinking to myself, "How can we do this better?" And over time, that's when landing in my lap was this resource by Cathy Fosnot called Minilessons. Jon, I don't know, have you had an opportunity to dive into Minilessons at all, or what's your experience there?
Jon Orr: We chatted with Cathy Fosnot on the website. She gave us a good snapshot of what minilessons are and from her description of them, it's not that I've used her resources in particular in my district or at my school. But that idea of a string of problems that are tied together, or this idea of these webs that stretch out. I think that part might be similar, but no, have not used those resources in my school.
Kyle Pearce: And to be honest, Jon, when you and I plan math units and we do our problem-based lessons, we're using a lot of the same elements in our lessons except here again, she calls them minilessons, so she kind of has this intentional minilessons baked in there and it's really helpful to help with number fluency and operations sense. But the part that I really love is the attention that she had paid and it really forced you and I to open our eyes, to this thing that could help a lot of students that might not be able to keep up with the mental math and just being able to do all this in their mind. Cathy Fosnot actually believes that when you're doing mental math, you're actually doing the math with your head, not just in your head.
I really like that and I actually used that line today in every class I went into because this was a new experience for them. What I was trying to give them the permission to do was to leverage strategies, not only in their mind, but also on paper and models. Those two things were things that I wasn't really paying a whole lot of sense to like, if you were using the Number Talk resource, there's definitely strategies baked in there. They have compensation, they have the commutative property built in. They have all kinds of things built in and they have models at the beginning of the book. But with the Minilessons resource, what I found is that every single minilesson is crafted with this string of related problems that you had had mentioned there, Jon, that really emerge. The intentionality is to emerge a big idea, just like in our problem-based lesson, utilizing certain strategies, so we're anticipating certain strategies might come up, some others will also emerge and we're going to do our best to help emerge a certain model.
Jon Orr: When I was thinking that those warmups, which were those website warmups, which we were calling getting kids to talk about math. Most of those are one off problems, one off estimation, one off which one doesn't belong. They weren't a string of problems. So, we were saying, the Minilessons is very focused. It's like let's develop, or there is developed, a set of problems all ready to go for teachers when they want to tackle a certain, or an idea, or a big idea. That's a really important idea for a math talk, right Kyle?
Kyle Pearce: Absolutely, yeah. So when you're going in, there's a lot of intentionality baked in there and you're hoping to emerge something. So, I'll give you an example. I went into a grade five class today who I knew hadn't been using this resource. Also, I had a hunch that maybe this class had not necessarily been using the area model for multiplication. So, there's a string of problems in the Minilessons resource that I can use, and there's actually many of them and they evolved. So, this is something you could do throughout the school year.
What we try to do is we try to give you a low-hanging fruit to start. It might be a fact that most students are going to know. So for example, we started with the context, context is also important, context of a box of chocolates.
So, you'll notice the context I picked, if I want to emerge an area model, if I want to emerge basically an array inside of an area rectangle, I want to use a context that's going to get kids visualizing that in their mind. So, it's kind of like you're leveraging a context to help students get nudged down this path without them even realizing it. Then they can articulate to us what their strategy is for three rows of eight chocolates. So, I had said, "I'm a chocolate freak." It's Halloween coming up as we're recording this and I said, "Although I'm going to be stealing all my kids' candies. I actually a bit of a chocolate snob and I like the chocolate that comes in those boxes, you know, the really expensive kind?"
Jon Orr: Right. So, I think what I'm hearing right here is there's some very intentional aspects of the Math Talks that's happening in the minilessons. Because if you said, "Let me throw down a bag of candies that might not nudge ... " I like that you use that word, it's like it nudges the kids to picture and visualize the model that eventually you want to show anyway.
Kyle Pearce: Yes, exactly. You imagine that it's like, if I want an area model, I want something that feels rectangular. If I wanted, for example, to emerge a number line, if I want that mathematical model, then maybe I want something more linear in nature. Maybe it's like jogging running, you're running a distance. And you're like, "Oh, when I think of running a distance, I don't think of a rectangle. I'm thinking more of like a line."
So when you think of these, now one thing that you don't necessarily get in the Minilesson book itself is the context, what these were crafted within some of Cathy's problem-based lessons. I think she pulled some of them out and added to them. So, the intentionality is that you're already using problem-based lessons and that you're creating context around them.
Jon Orr: Let me ask you this. So, a mini lesson or a math talk here is, starts with a big idea. This is an idea like I want my students to be able to multiply with an area model, or I want my students to be able to use a double number line to say, solve a proportion. These big ideas of our courses in our classrooms, in their content standards. Then the talk unfolds a strategy that nudges a strategy along, which will then evolve into a mathematical idea and there's a string of problems that make all of that happen. Is that fair to say?
If it, is my question, probably what everyone wants to know if this is something they want to hear about from you and us, and maybe from everyone else is, is this a full lesson? Does this take my math block from start to finish? Or is this still a warmup? Is this still something that I'm doing in 10 minutes?
Kyle Pearce: Yeah, absolutely. I'll be honest and say that you could do an entire lesson and probably early in the process as well, they'll go longer. It's kind of like you and I have talked about notice and wonder protocol, it's like the first time you ever do that in your class, it's going to take a lot longer because you want students to really become comfortable with the norms and how it works. But I would argue that you can fit these ideas in in much smaller chunks of time. However, if let's say, it's stretching out and students haven't emerged the big idea or the strategy, some teachers get worried, like, "Is this going to take up too much time?" Again, I feel like this is one of those cases where you and I say, "We don't not have the time." If number sense and fluency is one of the biggest pebbles in our shoe as educators, we always say students come to us without enough number sense.
Whether it's working with fractions, whether it's solving equations, because it relies on operations like multiplication and division, and solving equations and adding and subtracting on both sides. If those are the big challenges, then you have to start to wonder and weigh out your curriculum and wonder why are these other pieces here? A lot of times I think they're there as an excuse to do more number sense. Number sense is like the big, big one.
Again, we don't want to just be drilling and killing here. That's something that I think mini lessons and number talks in this fashion, this math talk idea we're trying to drive home here, I think when you do it through context, when you have that big idea ... And you had mentioned, I wanted to go a little deeper on the big idea too, because there can also be an idea ... If you think about it, the word that is awesome, and Yvette Lehman, one of our awesome Math Moment unit writers, she uses the word behavior a lot. I think she got that from Cathy, she's a big Cathy Fosnot fan as well.
The word is behavior. It's like, you want to emerge a behavior about mathematics that it's almost like you, "Okay, let's look at it this way. Okay, let's look at it that way. Oh my gosh, when I do this, this thing happens. When we do this, this thing happens." So, in today's number talk, when we did our string of problems, I started with three rows of eight candies. Then I went to six rows of eight candies. Then I went to 12 row of six candies. Then we went to, I believe it was six rows of ... I may have messed that up. Then we went to, sorry, three rows of 12 candies, so you see how we're doubling the second factor. Then we doubled one factor and halved the other.
Jon Orr: I got to write all this down.
Kyle Pearce: Yeah, yeah, yeah. I might even need to. So let me write this down here, so-
Jon Orr: Everyone listening right now, who's like me and who are not auditory learners are like, "I have no idea what he just said. I need to draw what he's saying and then I can see it." That's exactly what I need to do, Kyle. He's actually drawing right now. He's going to hold it up to the screen for me.
Kyle Pearce: Yeah, totally. This is what we did and then we went ... Interesting, yeah. So, what we went with was-
Jon Orr: While you formulize that, the important part here I think to note, is the string of prompts that Kyle's coming up with. They're hard to create because if you have the big goal in mind and you want the model to come out the way you want it so that kids can use it, and you want them to develop that model along the way, you carefully have to ... Well, you used a phrase before we started recording, Kyle. It was like breadcrumb them along. You breadcrumb them along, so that one prompt, it's low floor enough that everyone can get in it. But then you turn the dial up just a little bit more and then a little bit more. So, it's like you create this string of problems that will build upon each other. Then by the end, it was like, if you started with that one, you would have to show them all what to do. But because you started with these breadcrumbs, you didn't have to show them anything.
Kyle Pearce: No, totally. Exactly. For those who are watching on YouTube, you'll have an advantage on YouTube right now because I'm going to flip my document camera on for my screen, just so people can see. So, we started with three rows of eight chocolates. Students in this particular class, they all felt pretty confident with 24.
Jon Orr: What grade was it again?
Kyle Pearce: This was a grade five class.
Jon Orr: All right.
Kyle Pearce: Again, the numbers you choose, sometimes even in the string, I don't even think these were the numbers in the string. I actually looked at the string, looked at the intentionality and then I adjusted the numbers down just because it was my first time in this class and I didn't want to come in and potentially, maybe they didn't know this math fact, but I wanted to give them one that I felt confident that they would be able to come up with at first.
So they came up with 24, they shared their strategy and then basically, I nestled them along to the point where even though students didn't say it, one student actually said, he's like, "Well, I know it's 24." I was like, "Okay, so how are you going to convince me?" And they're like, "Well, I just know it's 24." When you think about that, it's like, that's not a bad thing that you know 24, of course, I want you to know that it's 24. But one thing that is, I guess, a little bit scary is that you know that, but you don't know how you could articulate that to someone, that adaptive reasoning piece isn't there.
I'm sure it's there, but he's just probably never been asked to share the why behind it for so long. It's just something that he just knew. But what I need to do is to get their strategy. Then finally some students said, "Well, I looked at it as well, there's three rows of eight chocolates in each row." They were like, "I'm going to skip count by eights." I'm like, "Oh great. Can you do that for me?" The student's like, "Eight," and then they pause, "16, 24." Okay, so there is my moment where I get the opportunity to try to get this model to emerge.
Even though the student didn't say, "Hey, draw me a rectangle." What I ended up doing was, "Okay, you said three rows. Is it okay if I draw three rows like this? Then what would I do to do your skip counting?" Then the student tells me, "Well, you'd put eight in the first row and then you'd do eight in the next row, eight in the next row." So it's like we bread crumb them from, "Oh, here's your strategy, you started with ... " Absolutely, really, you didn't even think about a strategy, but I've helped breadcrumb you along so that now we've got you to essentially an array, but I'm going to eventually ... We're going to eventually leave the actual dots behind. This is just to get people visualizing the box and then we're going to continue and then hopefully they'll be able to leverage the strategy moving forward and the model.
Jon Orr: Right. Now, let me ask you some structure problems here about what you did with your group today. So, with that problem, when you posed that problem, or the string of problems, they're all sitting down at their desks. Are they at the boards? I'm trying to picture the way you did this.
Kyle Pearce: Great question. The way we did it today, we're still in COVID protocol season. So, they were all at their desk and every class was a little different. I tried to fit into their regular routine if I can. So, I'm like, "What do they have? Do they have a math journal? Do they have a whiteboard? Are they allowed to write on their desk with erasable marker?" So, it was really, I guess what we're saying, is it can look a few different ways. I tend to do these with students individually at their desks. So to me, I look at this as an opportunity before going into, let's say a problem-based lesson, where everybody gets a little bit of time to do a little bit of, we'll call it independent thinking, and then sharing to the group. So, that's how I do it. It doesn't necessarily mean that how it has to happen, for sure.
Jon Orr: Just to be clear, so when you're asking the student who's describing their three rows of eight chocolates, and you're saying, "I'm going to draw these rows," that's whole group?
Kyle Pearce: Exactly. So, I'm doing this to the whole group. A lot of times, the intentionality there on the teacher side is I want to, again, float this model and I want to leave this up as almost like ... Again, I could have done this the way I used to teach, was I'm going to define what an array is. When we multiply, we draw it this way, but really what I've done is I'm like, I'm taking your voice and I'm going to try to represent your thinking using this model. So, I have a very intentional purpose here, much like when we do a problem-based lesson, we have models in mind. We have strategies in mind. So, I'm going to try to help pave this path and get students thinking.
Then after, too, we're going to ask the student, "Does this represent your thinking? Can you see your thinking in this model?" So, it's like the questioning is very intentional not to say, "Is this how you did it?" Because I know the answer is no, because the student said, "I just know it's 24," but now we've given them the opportunity to go, "Do you see your thinking here?" Now they're like, "Well, yeah, I do see it." Then you can ask another student for another strategy, and so on and so forth.
Jon Orr: So, asking those types of questions, Kyle, getting kids to ... When you model, I can see that the benefit is that you're introducing them to the model, even though they might not have created that model. I think we get a lot of questions about that through our Math Moments Academy, but also questions about our podcast and just generally on our Facebook group, kind of thing like, "How do I get kids to do more modeling?" It's almost like they want to say, "How do I force them to use a model?" And I'm seeing, you're uncovering it for them, and then the fact that you're modeling it for them will hopefully lead them to do it the next time in that way.
Kyle Pearce: And the beauty is, again, and if the string of problems are crafted in a way that they're related and intentional. So the next place we went is six rows of eight chocolates. So, it's sort of like going to your point about how do I get kids to want to use model? Well, here I've dangled this here. You know that this is, okay, here's my three rows and here's my eight chocolates. It's almost like a lot of students right away, they're like, "I can see the chocolate." It's like they know the context and then right away they go ... even if they're not thinking multiplicatively yet, they see that, "Oh, okay. I just need more rows."
This is where we can start extending this model and then we can also then abandon a bit of the array. I've shown the array here, but now I might ask the students, "Okay, so Tommy says to add three more rows," another student might say, "Take a screenshot of that and duplicate it, double it." I'm like, "Oh, interesting. Okay, so we're going to double that. Is it okay if I ... " and you ask them for permission? "Is it okay if I skip drawing the chocolates? Is everybody okay with you see there's eight in there?"
And this is where you're helping get them to a more abstract representation. So this is much more ... I mean, it's not concrete, but it feels more concrete. It's closer to concrete because you can see it all. But now it's like, I'm pushing them. It's like taking the training wheels off a little and we go, "Okay, so now I have six rows. I wonder how many that's going to be?" Almost instantly, students are realizing, "Oh I've doubled my rows. I can see that I've doubled the box of chocolates, so I'm actually doubling my number of chocolates."
We start to progress here and then we move to, "Okay, how about this one? 12 rows." I say, "Okay, that's not enough chocolates. I want more chocolates. I see another box. And I see there's 12 rows." And then the students are like, "12 times eight is what it's going to be." I go, "But there's four chocolates per row?" I'm like, "But I've 12 rows, I'm feeling confident. How many people are feeling confident that there's going to be more chocolate? We're in good shape, right?"
Then all of a sudden you start to see some kids' heads turn sideways and they go, "I don't think so." Some students are starting to visualize what's happening here. "Oh my gosh, I've doubled my factor, but I've halved-"
Jon Orr: Of rows.
Kyle Pearce: Yes, I've doubled my-
Jon Orr: You're drawing some arrows there.
Kyle Pearce: Look at that. It's like, I've doubled ... Oh my gosh, I've doubled my number of rows, but I've actually halved my number of chocolate. So, it's almost like we're taking this piece. I love when someone says, "It's like, you're taking this chunk and you're moving it down here." So I say, "Oh, so what is the answer?" And they say it's 48. And it's like, "Oh, how many people knew what 12 times four was first?" Some kids, "Okay, sure." You keep extending this and you go, "Okay, how about 12 and eight?" A lot of students are like, "I don't know what that is," or continue extending, continue doubling one of these numbers and they start to see the pattern emerge. They start to see the behavior of math emerge.
So, here we've got a strategy of, okay, so I've got my model. So I've got an open array or an area model, we can call it. And one of the strategies that we're focusing in on is this idea of doubling and this idea of what happens when you double in half. If I double one factor, I double my quantity or my product. If I double in half, then nothing happens. That's interesting because then you think of how you can manipulate any multiplication problem to be easy. I can do like 18 times eight, doesn't have to be 18 times eight. It could be nine times 16. Right away, I can leverage these tools in order to make my life easier and make multiplying any number easier, or any two numbers, I should say, easier.
Jon Orr: I think the important part here is it started with a big idea being ... You just let us know what the big idea was, this fluency between with multiplication and number and doubling and halving and the relationships here. That's a big idea. One question I think teachers might have is, because it is hard to come up with those strengths. What would you say is a tip to give a teacher to say, "Tomorrow I want to do a math talk like that. I've got my big idea." I want you to think more general because somebody might be on measurement. Somebody might be doing proportions. Somebody might be doing solving equations, somebody's doing fractions. So, I'm just wondering if you can generalize a good tip to go, "Look, I want to develop this string of problems to build the model in, but then also unveil the big idea I want to come out." That's a lot. What would you recommend for teachers to get started in this?
Kyle Pearce: Honestly, it's a great question. I would say to get started is try not to recreate the wheel. There's a lot of great tools out there. I mean, we'll give Cathy a bit of love here and these Minilesson books, they're available on Amazon. Here they're on Heinemann's website, definitely worth checking out. I've learned a lot from them. I feel like my practice has evolved in using these tools. Another tool, if you don't want to spend cash, is the Math Is Visual website, right?
Jon Orr: Yeah, let's come back to that just for a quick thing. But I guess what you're saying is you're at a place because you've done a lot of learning. It seemed like it was so natural for you to be like, "I'm going to make this string up of problems because I know I want to double in half and you had just built it almost on a spot with us even." That's just because you have a comfort level of that problem string, which you've learned through these other resources. It's not like you were just like, "I'm going to stumble across this and I just whip these out whenever I want." It's like, "No, Kyle has read about this through Cathy's program. He's used the resources, the prebuilt ones she's already used, to help create his own."
That's I think what, as a listener, you'd want to grab your hands on, Kyle. We're throwing the link in the show notes, but also yeah, the Math Is Visual website is built for this and it's got a visual spin on it. So, when he was outlining the chocolates, he's drawing the chocolates on the board. You can also start your own math talk, but also have all the visuals built for you so that you can put it up on the screen, so that part of that chocolate array is already nudged in there because the pictures are nudging students to build towards that model anyway.
Kyle Pearce: Yeah and when I create the Math Is Visual website, I've tried to embed all of this learning that I've done over the years and I've tried to make it as, I guess, accessible for educators as possible so that it's accessible for their students. So, up on the screen for those who are watching instead of listening, you'll see there's a Math Is Visual prompt that's ... it's about caterpillars. Basically we give you a visual of what's going on there. There's a pause prompt, so the teacher can pause it. What that does, to me anyway, it's a nice entry point for the educator who might be new to this routine and they're sort of like, "I'm not sure if I'm confident enough to create the context on the spot or to be able to model it." This will give you , not only the prompts, but also it gives you a teacher guide that outlines the different, big ideas and what we're after here and what strategies might emerge. So, these are here for people to leverage and this is actually a solving equations math talk.
Jon Orr: The one you're showing on the screen right now?
Kyle Pearce: Yeah, the one that we're up on the screen and basically the equation that merges four M plus two equals 30, and we leverage a double bar model, which is kind of like a more concrete, double number line in order to solve this problem, and we show it symbolically as well. So, you as the educator, it's great if you can model it on the board, but this is a great spot for you to almost get some practice. So you could do this ahead of time, you could show this after, students can reference it after. The beauty is, is that all of these newer Math Is Visual prompts are actually a little snippet from our problem-based units that we share on the Math Moments site. So, this is here for you. If you want to go down the rabbit hole, you click on the link and you can do a whole five day unit that sort of builds on these big ideas and these models.
Jon Orr: Right, so there's lots of resources out there. You do not have to build your own. Even though you might want to try, eventually. Once you start to see how these progressions are built by seeing pre-ready made ones, you might say, "Hey, I can do that on my next one." Or, "I might give it a shot." I think that's a great strategy because the more comfort you get with building problem strings is going to be better for you and also your students. But just a quick recap here, Kyle, on building math talks in your classrooms, big idea, super important. Don't go into a math talk, not knowing what your intention is. What is the learning outcome that you are looking to have brought forward. You are going to make sure that you want to highlight a strategy so that you can build in the mathematical model that you want to showcase on that particular math talk. Just to recap what you said, it doesn't have to be a full lesson. It could be a full lesson, but it also could be part of your lesson.
Kyle Pearce: Absolutely, absolutely. Those are huge ideas for myself. Again, I look at them as more intentional than just an average warmup. Another piece we should also mention, it doesn't necessarily have to lead into today's lesson. You'll notice, if you go to our website and you look at the problem-based units that we have. If there's a five day problem-based unit, we don't necessarily put a math talk on every day. If it's a problem-based unit lesson, we usually use our notice and wonder as our warm up routine and get kids estimating. Then on day two, when we are planning to go deeper with more purposeful practice, that might be a great opportunity to do one of these math talks, because then you're setting the stage. You can drive home a point that we learned yesterday and build on it and then give students a little bit of time for purposeful practice.
You could pull a small group and ensure that students are where you'd like to see them and nudge them along their journey. Then maybe the next day you go into another problem-based unit. So, there's no hard, fast rules on it. But one thing that we now believe is that we can leverage these math talks as an opportunity to drive home this number sense fluency and operational fluency. I don't want to be, dare I say, donating some of my class time because everybody says they don't have enough time. So, if I'm going to just do a random routine because for, we'll call it engagement purposes, or just to get kids talking, that's great but I think we can build that into other aspects of our lesson.
If we keep them contextual, if we keep them problem based, then I might be able to save some of that time and I might be able to insert maybe more of these intentional math talks so that my students can build these strategies, build confidence too. The confidence kids have when they're solving pretty complex, or we'll say big multiplication problems with big factors, or division problems without long division. These are skills that we're giving students, so that flexibility builds, that confidence builds, and they can articulate what it is and why it is that they're doing what they're doing. I think that is such a gift that we can provide students. When I'm back in the classroom, which I hope is in the next year or so, I want to be doing this, like I say, as often as I possibly can.
Jon Orr: Awesome. Great stuff there, Kyle, thanks for sharing your insights on math talks. Hey, what do you think? Is this something that you're going to give a try? Is this something that, maybe grab a partner, grab a colleague to try this with and say, "Hey, look, let's plan one together." Or, "I'm going to plan one. You plan the next one. Let's do that." You want to try to make sure that you're not doing this alone, that can make a big difference, is making sure that you have someone to chat about with. If you need somebody, we are definitely available. Hit us up on our social media. We are at Make Math Moments on Twitter or Instagram. We have a free private Facebook group, that's a great place to ask a question because the members will jump in even before Kyle and I probably even get there. Usually that's the case, is that you are rescued with any questions you have on anything that you have been trying in your classroom. So hopefully, you will try math talk this week and let us know how it goes. You can email us as well.
Kyle Pearce: Awesome. Friends, listen, if you're listening on a podcasting platform, hit that subscribe button, especially on Apple Podcasts. That will help us reach an even wider audience of Math Moment Makers just like yourself. We want to make sure that all educators around the goal have access to high quality professional learning. This is just one way that we hope to help meet that goal. If you're on YouTube watching right now, well, hello, I'm waving to you right now. Look at that. Hit that subscribe button and also hit the notification bell. That will let you know when a new YouTube video comes on. So, not only do we do the podcast us every week, we've got a new YouTube video coming out each and every week, that's nice and short and it gives you some tips.
We actually had a recent YouTube video that we shared, which was a clip from one of our Q and A sessions with our academy members, where we were doing a math talk, but we did the math talk with the group of educators and we worked through it with our teacher hats on and our student hats on. We talked about all or some of these elements, as we've heard here in this episode.
Jon Orr: Awesome. We will put those in the show notes, which you can fine with full transcripts from our episode here at makemathmoments.com/episode156. Again, that's makemathmoments.com/episode156, to get links from this episode.
Kyle Pearce: All right, my friends. Well, until next time, I'm Kyle Pearce.
Jon Orr: And I'm Jon Orr.
Kyle Pearce: High fives for us.
Jon Orr: And a big high five for you.
Sign up to receive email updates
Enter your name and email address below and we'll send you periodic updates about the podcast.
DOWNLOAD THE MAKE MATH MOMENTS FROM A DISTANCE CHEAT SHEETS
Download the Cheat Sheets in PDF form so you can effectively run problem based lessons from a distance!
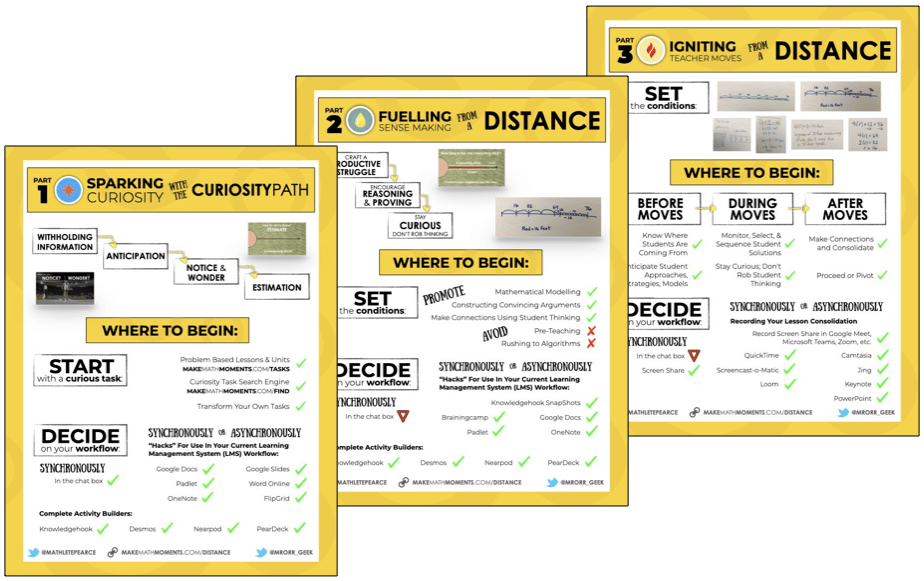
UP YOUR DISTANCE LEARNING GAME IN THE ACADEMY
There is a LOT to know, understand, and do to Make Math Moments From a Distance.
That’s why so many Math Moment Makers like YOU have joined the Academy for a month ON US!
You heard right: 30 days on us and you can cancel anytime. Dive into our distance learning course now…
Thanks For Listening
- Apply for a Math Mentoring Moment
- Leave a note in the comment section below.
- Share this show on Twitter, or Facebook.
To help out the show:
- Leave an honest review on iTunes. Your ratings and reviews really help and we read each one.
- Subscribe on iTunes, Google Play, and Spotify.
ONLINE WORKSHOP REGISTRATION
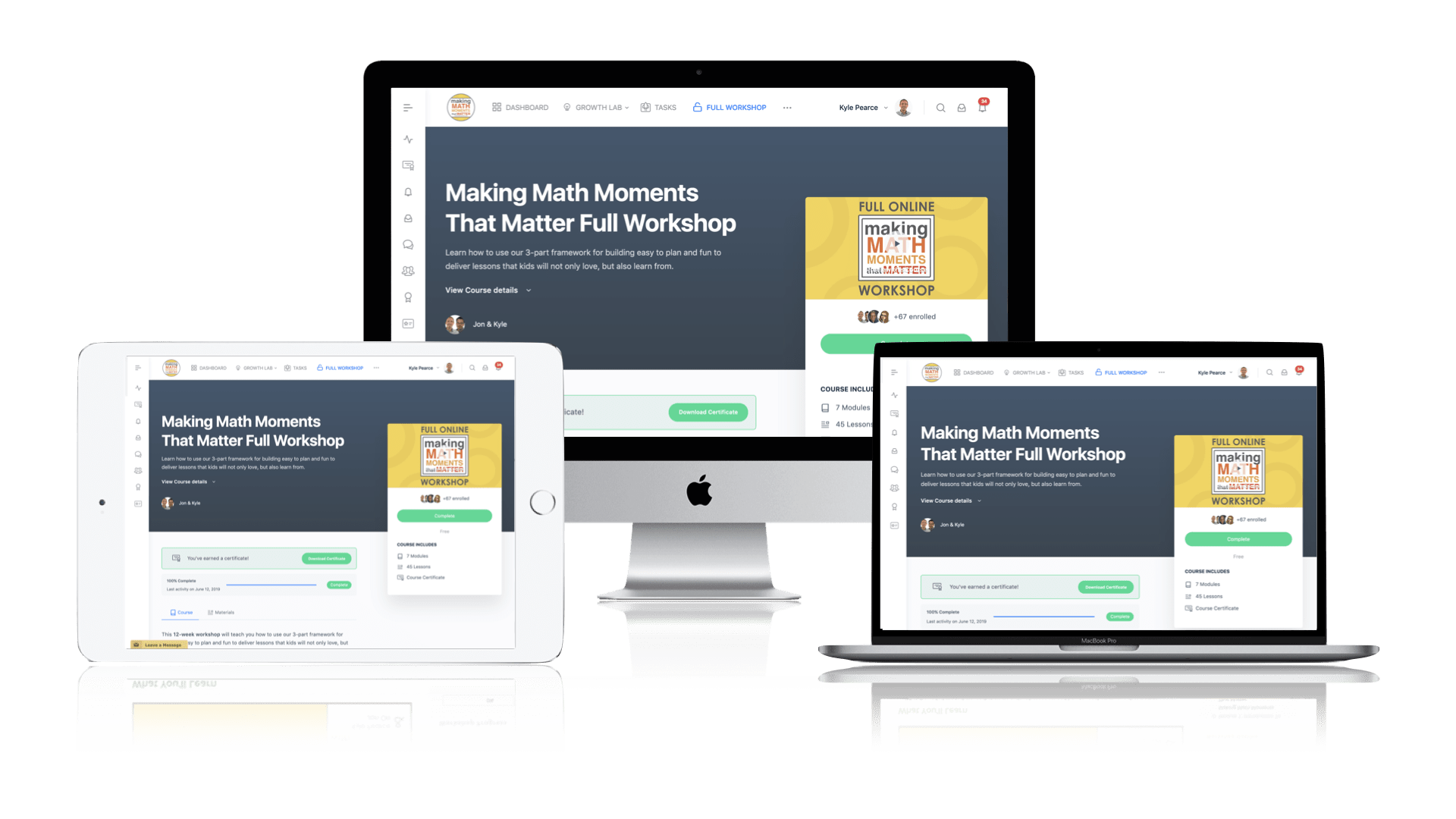
Pedagogically aligned for teachers of K through Grade 12 with content specific examples from Grades 3 through Grade 10.
In our self-paced, 12-week Online Workshop, you'll learn how to craft new and transform your current lessons to Spark Curiosity, Fuel Sense Making, and Ignite Your Teacher Moves to promote resilient problem solvers.


0 Comments