Episode 164: Teaching Financial Literacy Through Mathematics – An Interview with Philip Dituri
LISTEN NOW…
WATCH NOW…
We speak with Philip Dituri from FiCycle.org about financial literacy: while so important in the real world, but is somehow rarely discussed or taught in schools. Philip shares how we can answer the common question “when will I ever need this in real life?” He shares how teachers can blend their existing curriculum with contextual lessons based in personal finance, and we discuss why we need to prepare students for life, not just tests.
You’ll Learn
- How we can answer When will I ever need this in real life?
- How I can blend my curriculum with lessons based in a personal finance context;
- Why we should be teaching financial literacy and algebra in concert; and,
- Why we need to prepare students for life – not tests.

FULL TRANSCRIPT
Philip Dituri: Understanding the power of investing in the market over the long term is directly related to understanding the power of how quickly exponential functions grow. Those are directly related concepts, the same conceptual understanding. So by taking a theoretically grounded economic theory and personal finance and hanging the math on it, we know crosstalk-
Jon Orr: Today, we speak with Philip Dituri from FIcycle.org about financial literacy. While so important in the real world, but somehow Kyle, it is rarely discussed or taught in our schools. Philip shares how we can answer this common question, when will I ever need this in real life?
Kyle Pearce: Yes. In this episode, Philip is going to share how teachers can blend their existing curriculum with contextual lessons that are based on personal finance. And, we discuss why we need to prepare students for life and not just that next math test. All right friends, let's do this.
Jon Orr: All right.
Kyle Pearce: Welcome to the Making Math Moments That Matter Podcast. I'm Kyle Pierce.
Jon Orr: And I'm John Orr. We are from MakeMathMoments.com and together
Kyle Pearce: With you, the community of Math Moment Makers worldwide, who want to build and deliver problem-based math lessons that spark curiosity ...
Jon Orr: Fuel sense making ...
Kyle Pearce: And ignite your teacher moves. Math Moment Makers, we are super excited to dive into another video podcast episode with ... I'm going to call him our friend now ... Philip, who is from FIcycle.org. And, I had the opportunity to have a discussion with Philip about their curriculum that essentially embeds financial literacy into the Algebra II curriculum. And my gosh, it was awesome. It was great to connect and we thought, you know what? We're going to have to bring him onto the show and introduce him to John and the Math Moment Maker audience.
Jon Orr: This is an exciting conversation because I think especially in high school, coming out of high school, you think that our students should have this sound basis of literacy and financial decision making. Yet, if you had taken say the college track or the university level track, rarely do those students actually get instruction on personal finance. I find here in Ontario, it's a group of students who are going to workplace right away or preparing for real world and not heading off to post-secondary education that get that education. But this other group of students, it's almost like we just assume they're going to figure it out on their own. And, I think this conversation is great to give teachers resources to help teachers kind of help all groups of students get what they need about personal finance. So, let's get right to it and here's our conversation with Philip.
Kyle Pearce: Hey, Hey there, Philip, thanks for joining us here on the Making Math Moments That Matter Podcast. I'm super excited to chat with you. A few weeks back we had the opportunity to connect when I was learning a little bit more about what you and your project, your work is all about. And I thought, you know what? This is going to be a great fit for the Making Math Moments That Matter audience. So, how are things going in your world right now? Where are you coming to us from right now?
Philip Dituri: Things are going great. I'm coming to you from my home in Brooklyn, New York, and yeah, having a good time. It's been a good year so far, considering everything. Schools seem to be in a good place, better than I may have guessed they would be at this point in the year. So it's always nice to hear that from all the people I work with.
Jon Orr: Phillip, tell us a little bit about yourself and your journey. Fill our listeners in on your background, your role in education and where that stands right now, and give us a little backstory on the journey here for you.
Philip Dituri: Yeah. So I was an undergraduate math major who just really loved math and I didn't actually start off thinking I was going to become a teacher. In fact, I promised my parents, who are both educators, that I wouldn't when I went to college. When I decided I wanted to-
Jon Orr: They were warning you, "Don't go there."
Philip Dituri: Yeah. They're both educators who love it. In the end, they were very happy about it. But at the onset of my education, I went to NYU for math, and they were very excited about that and they said, "Well, if you're going to go to NYU for math, just make sure you don't become a math teacher. It's not necessary." And in fact, I think they were very wrong. My passion for math grew a lot while I was there at NYU. I started off doing some other things. I interned at an investment bank. I worked at another office while tutoring at night. And one of my friends commented on that usually people don't like their second job. People don't go to another job and get jazzed by it, and that I might enjoy teaching. So, I changed careers, became a teacher. I taught in New York City public schools in downtown New York at a Title 1 school for 13 years, where I was a teacher, then a coach, head of the department, while at night I got my PhD at Columbia University in mathematics education.
I eventually left this school to become a visiting professor at Fordham, where I got to interact with teachers similar to how I might with cooperating teachers or with new teachers that we would hire, but in a much more formal setting as a professor. So, that was really fun to do that. And now I'm the Director of Education at FiCycle, which is how I come to talk to you guys today. I'm an educational consultant, work with schools, provide professional develop and do an array of things for schools and districts all around.
Kyle Pearce: Awesome. And I think that's a great summary based on the conversation that we had had. I really thought it's really nice when you see that you've gone into the industry you've gone into in particular, like investment banking. So you have your boots on the ground, you know what's going on in that world, and then you leave that ... I'm going to guess that you're probably making a pretty healthy salary and decided to go into teaching mathematics. And now, we come full circle and you're here at FiCycle, really trying to bring financial literacy into the forefront of our mathematics education. So I want to dive deep into that idea, but before we do, we have to ask you something we ask everybody who comes on the show, and that is what is that math moment that sticks out to you? You went to ... You said Columbia? No-
Philip Dituri: I did my PhD at Columbia University at Teachers College and I did my undergraduate at Courant Institute at NYU in math.
Kyle Pearce: There it is. So NYU, you ended up doing your math degree so there had something, when you look back on your K through 12 ... I'm going to limit you to your K through 12, but if you must go beyond that, that's fine too. What is that math moment that sticks out in your mind? For some educators, it's a positive moment, for other educators, it's maybe something that they maybe have learned from, and maybe wasn't so positive in the time, but either way, I feel like we walk out of that experience learning something. What's that moment for you that comes to mind?
Philip Dituri: Man, I actually think there's a lot of them, but at the moment what comes to mind is I was in 10th grade in 1995. I had a teacher, Mandy Gersten, who was great. I had a lot of great math teachers. I was very blessed in that way. And I was the kid who sat in the back of the room. I would routine sit in the back and I would figure out what the homework was, and then I would do the homework while the teacher was trying to teach us the thing that was on the homework. So you'd figure it out first from the textbook while they were talking. Teachers make terrible students in general. I was no exception to that rule, but my teacher gave us this activity, which was awesome.
She sat us in groups and she gave us this open-ended problem solving activity where before we knew anything about combinatorics, or anything like that, the unit before that, she gave us Pascal's Triangle and just told us to notice as much as we could. And, as someone who was like, "All right, next chapter, this isn't the thing in the next chapter, how do I notice what I'm supposed to notice?" And so-
Kyle Pearce: I'm not noticing anything.
Philip Dituri: It was fun. Right. Well, it was fun. Obviously, as anyone who's ever looked at Pascal's Triangle knows, there's so much to notice. It's so interconnected and deep. It's such a wonderful, simple activity. Discovery stuff, genuinely exciting. I felt like I was doing something originally. Up to that point, math had felt like more like regurgitation. I had some good teachers but I still was like, "Oh, it's like the times table. If I can memorize all this stuff and then do all this stuff, I'll be fine." And so, that was really fun. It was my first real brush, I think, with proof, reasoning, non-routine problem solving, open-ended problem solving in a group setting. Man, it was awesome. If I observed that lesson right now, I would be so complimentary to that teacher, and this was in 1995. We're talking 25 years later, so that was pretty awesome.
And, that impacted me in a really positive way. I also just thought math was hard at times and that school wasn't as hard, and so I had a respect for math. When I went to at NYU ... I know you limited me to K through 12. I'm sorry ... I often felt like my degree at NYU was one of the more hard things I've done, and I've done a lot of things since then and I have a real respect for mathematics, for mathematicians, for anyone who engages in genuine discovery.
Jon Orr: I think Kyle and I, from our conversations, it seems a lot of the times we talk with people who are also math majors or have math degrees and who went into teaching have very similar experiences with the mathematics at that level. And, I think we both can sympathize or emulate this feeling of sitting in math class. And, I have memories exactly like yours, Philip, where I would try to get the homework done before I could go home because to me, math was a get done subject and if I could get it done in class, I didn't have to do it at home. And a lot of times, I could beat the teacher to the right spot. I remember the teacher trying to go through a proof and kids were like, "Well, we're trying to copy this proof down." I'm like, "No, Dave, he's just doing the proof. Here's the formula over here."
I was the kid who wanted to skip all of that because I view math ... and, I played that game. I played the game of math is let's just get these questions done. I don't feel like I had an experience like you had in high school. It wasn't until I think I started teaching where I had these experiences where it opened my eyes to so much wonder and so much beauty that math can have and how we can open those eyes for our students.
I'm wondering that moment that you've just shared with us from your high school career, that lesson from Pascal's Triangle, I'm wondering in your 13 years teaching, did that moment influence you in that? I know I just shared my moment there, too, that said I viewed math a certain way and then when I became a teacher, I actually taught math like that, too. When I first started, I wasn't a teacher who was "We're going to jump in and do all of these investigations." I was a "Let's just get right to the examples" teacher for a long time.
And, I'm wondering were you like that, too? Or, were you like, "Let's explore Pascal's Triangle lessons right off the hop." Or, did you come into that ... I'm curious there. I'm always curious about new teachers and what's happening with how they think about their past math careers into their teaching career.
Philip Dituri: Yeah, that's a great question. Working with new teachers a lot, I often talk about how hard it is to do anything other than how we were taught. Right? So especially if you ask someone who is your favorite teacher and you ask them what their teaching style was, I think they're 75% likely to just emulate that. Fortunately, I think people tend to like good teaching, but growing up, it wasn't always the case that everyone was exposed to all of the ideas and best practices that we're aware of today. So the answer is I think my coach would tell you that I had very good instincts, but I would tell you that I was completely clueless. I had tutored a bunch, and so I was sure that I knew how to help kids and I think a lot of teachers who, when they start, if a student would say something correctly, I might feel uncomfortable if I then didn't repeat it.
It was a little ridiculous. I quickly learned and grew ... I think I mentioned I was in a Title I school in lower Manhattan, and it was our first year and there were 11 teachers on staff and 10 of them, it was their first time in the position, including all of the administration. So it was a rough first year. I remember I started engaging in collaborative learning, not because of this wonderful story I just told you, but because I literally couldn't get my students attention. But I could get their attention in groups of five if I went to each table. And now, outside of the things we're going to be talking about today, combining algebra and financial literacy, I'm pretty well known as a consultant for collaborative learning and problem solving. And for me, that stuff was largely out of necessity when I first started doing it.
I think I was really receptive to a lot of these ideas because I had such good teachers, because I had some of those experiences. I think the first time I tried to engage my students in real non-routine problem solving, it was terrifying to give them that freedom and to not know where they're going to go. And if you're not an experienced teacher and you're new, to not know if you're going to know how to handle the teachable moments they take you to. But, it's just as exciting in the end once you do it. It's just as exciting to engage your students in non-routine problem solving as it is to engage in it yourselves. It's so exciting to see where they run with it and where they go with it. So I would say that I have to audit and call my first principal who I still talk to, and my coach who's still my friend and ask them, but I would say that by the end of my first year, I was more aligned towards these ideas.
But coming out the gate, I was like, "Oh, I'll give them a grade and that's why they'll do their work. And, I'll show them how to do it and then they'll know how to do it." What? That's teaching. I had no idea what I was doing when I started.
Kyle Pearce: Isn't that the way it works? That's I thought, I know that.
Philip Dituri: The math handbook. I have a crazy story where I actually started teaching it without any education-education so I really was dropped into the deep end. I was just very lucky that I had a fantastic community that I happened to be dropped into.
Kyle Pearce: That's fantastic. And it's interesting because even though you mentioned the word necessity, almost like some of this had to happen, otherwise you weren't going to survive it. I wonder though, I know how long it took myself and I know it took John a long time as well to really start realizing that there was an issue with the way we were trying to deliver our programs. And for you, it sounds like it happened at least relatively quickly. I don't know if that's because maybe having experience in the industry, you're more a mature adult. I'm not sure if those things have something to do with it, but maybe that math moment had some role that maybe is you're unaware of, that it's unconsciously taking over.
Because like John, I had great teachers and I loved a lot of the math teachers I had, but I liked them as people and I think they did an amazing job, but they were less investigative. They were less exploratory and more this is how you do it. But, they did a really good job and they had really good intentions. So, I just didn't know what that world could look like to even give it a chance. So bravo to you that you were able to figure that out, and it sounds like within a reasonable amount of time. I think what I'd love to do is to be able to dive into ... You had mentioned it ... Algebra I and financial literacy. You had already given us a bit of your backstory talking about how you were working in finance, and then you come into education. You're teaching in the math classroom.
I want to know at what point ... Did you know before you entered into this role of being a math teacher that financial literacy was essentially absent from the math curriculum or was it after doing the work and realizing, "Hey, when are we going to talk about finance?" Tell us a little bit about that and how that evolved to what you're offering through your program at FiCycle.
Philip Dituri: That's a great question. Thank you. I should clarify, I interned for two years in investment bank while in school. And so when I finally went to teaching, every math teacher gets asked this question, when am I going to use this in life? And I was not an exception. And after teaching for a little while, you have some good answers to that question. Maybe some of them are pithy, maybe some of them are honest, maybe it depends on the topic you're teaching, but I suspect that my having to have a collection of responses to that question is a real failing of our approach to mathematics education. I shouldn't have to have a collection of answers to when is this going to be useful in life. So when I was a classroom teacher, I wanted that not to be a question. And I focused a lot on trying to provide my students with relevant and real world examples, student-centered tasks, modeling ... I mentioned that I engaged them a lot in collaborative learning.
That's how real math happens. People work in teams in the real world. And in general, I tried to place math in a context for my students where they could connect with it. Sometimes because it was silly, sometimes because it was interesting, sometimes because it was very relevant to their lives. And, to see how fun it was. It was very important to me to say, "Well, where's the fun in this? Why is this interesting?" Because math is fun. That's an assumption that I have with my class. And, I found that the more I engaged my students in these ways, the less they asked that question, and that was very powerful for me. So when I met Andrew Davidson, who was the founder of FiCycle and the first one to conceive of our curriculum and our general approach to teaching algebra and personal finance in concert, he was really excited about a lot of the same things.
And, he was very articulate about how he thought that the particular application of mathematics with personal finance could solve a lot of the problems that I was seeing in mathematics education. So, I was very excited by the things Andy was talking about so we started working together, with Andrew Davidson and Jack Marley-Payne, who's the current director of research at FiCycle, on the curriculum. And the more and more I worked on it, the more and more obvious it was to me that this was a real fantastic approach to teaching algebra and financial literacy, both because of the experiences that I've had ... It checked off a lot of the boxes of things I would try to do with my students, but I felt like I always had to try to infuse into the curriculum instead of just being present in the curriculum.
But also because at that point in my career being in somewhat of a leadership role, I knew that logistically wanting to teach personal finance would be really hard and that by combining it with mathematics instruction, it didn't require extra time in the school day. Math was a class that everyone had, but the school I worked at was a design school and we treated design like a content class, and as a result, we had a real terrible time with scheduling because that is not one of the major courses that kids are supposed to take every day according to New York state, where we are. Adding a course to the curriculum has a real opportunity cost. Time is a very valuable resource in schools, and so by combining mathematics with personal finance, it seemed like a really exciting way to give kids some of the real world skills they needed with some of the math that we were already teaching them.
It was exactly what I was trying to do in the classroom. So having things be interesting, relevant and real, no one turns and asks you, "When am I going to use this in life," when you're working on personal finance with your kids because it's really obvious. So I think meeting Andy and starting to work on it was when I got really excited about it. It was a good fit because by the time I had met Andy, I was already doing things along these lines. I was already trying to figure out where is log scale relevant? Well, if you look at the history of the stock market in a linear scale, you can't even see the biggest drop in the history of the market. If you look at it using a log scale, it's very obvious, right? That was an activity I already had in my class. That's now an activity in FiCycle because it makes tons of sense.
And, having that consistent application solved the problem I was always having of trying to bring in relevant things from disparate places, having this one consistent context solve so many problems of trying to bring this work together.
Jon Orr: That is interesting because I think a lot of teachers try to, or realize that they'd like to bring in personal finance, or maybe it's part of the curriculum. I know here in Ontario, we've got a new grade nine curriculum and it has personal finance built right into it now. And, in the past years it wasn't. So that's exciting or us to have that in here, and I think teachers are like, "Okay well, I've got to pull in some personal finance from somewhere, so do I just pull this lesson in and then teach it? And then, how do I do that with all my other expectations?"
Philip Dituri: Is it a unit on personal finance? Does it have to be its own thing over here and then I do these other things over there?
Jon Orr: Yeah, for example, you have the exactly where you have this log scale and it's like, "Okay, that might fit in my logs unit," but then that part's done. Or, do I have to be like, "Now I have to figure out where's a lesson that I can fit in over here." I'm curious, what's your experience with embedding it everywhere? Or is it like, "Hey, we've got a couple lessons here that go in slots A, B, and C and one down there in G."
Philip Dituri: Right. No, that's a great approach. I think I'm going to answer backwards. I'm going to back up through it. If you can't do a full fledged approach, anything you do is better than nothing. These are important life skills. I was listening to a podcast you guys did with some finance guys about personal finance for educators. And I think that they talked a little bit about this, but this is math that kids already know, and you can use it to understand things we have to do in the real world. So you're already teaching your kids the math, helping students transferring that knowledge to something relevant is the work. So, FiCycle is roughly an Algebra II course, and basically what we do is we try to integrate the financial concepts. I think instead of trying to think of it as like here's my algebra curriculum and where can I infuse it with math? ... Because I think that's what a lot of people do is you take your curriculum, you try to infuse it with stuff.
And I think that's why we end up with word problems with in this chapter, you're fishing and this other problem you're making acne widgets, and this other problem, maybe you have a bank account. So instead what we did is we did the reverse. So we started with theoretically ... the course itself is theoretically grounded in a Nobel Prize winning economic theory by a guy named Franco Modigliani. He has this lifecycle hypothesis of saving. And what he says is that in order to navigate your financial life cycle as an individual, you need to understand two principles. The first is that you can transfer consumption through time. What do I mean by that? I mean that when I was a young man, I was able to have my money travel through time.
I borrowed it from my current self in the form of a student loan. I was like, "I didn't make this money yet, but future Phil will. Give me that money I need right now, future Phil, please." And I borrowed it from future Phil.
Kyle Pearce: How did future feel about that? That you were taking his money?
Philip Dituri: That's future Phil's problem. No, no, no. Actually, this is how you might handle that conversation in a typical personal finance course. But, if you've taken FiCycle ... If young Phil had taken FiCycle, he would know that actually future Phil's life is better for having made that decision. There are times in life when it makes sense to spend more than you have. That's not what we usually teach people in personal finance. We usually teach people this rule like, "Be thrifty. Never, ever spend more than you make."
And then, kids are like, "Okay, great. I just graduated high school. It's time to make my first financial decision. What should I do?" And every adult is like, "You should spend more than you make." And, I don't think it's lost on anyone. I think I actually am better off for having made that decision, and math can show me that. The math I learned in high school can make clear why I'm better off.
But, I'm digressing. So the other way I can transfer money is from the present to the future. I can give money to future Phil, which is what I'm doing right now in the form of my 401K or my retirement funds, or if you're a teacher, your pension. I know you have a pension in Canada. Or, in Ontario, I think. Those two principles are what Modigliani said we need to understand to understand our financial life cycle. And, he won a Nobel Prize for this.
So what we did, instead of trying to take math and put finance in it, is we hung all of the standards students need to learn in Algebra II on this theoretically grounded approach to understanding personal finance. And, we made sure that we covered it. So it works very well because not a lot of people know this, but many of the tools of algebra were developed to meet the needs of personal finance, or to meet the needs of finance and economics. So as a result, the conceptual understanding underpinning the math and the conceptual understanding underpinning the personal finance is the same conceptual understanding, or it's mutually reinforcing. Understanding the power of investing in the market over the long term is directly related to understanding the power of how quickly exponential functions grow. Those are directly related concepts, the same conceptual understanding.
So by taking a theoretically grounded economic theory and personal finance and hanging the math on it, we know that we've covered all the math. We have a lot of standards based curriculums that we can look at and see what they're teaching in Algebra II and make sure that we're covering the mathematics that kids need. I think algebra is somewhat codified at this point. You can trail topics off to a math teacher in different places and they'll agree about what an algebra topic one, topic two is is most cases.
But then the harder part, which I think teachers sometimes struggle with, especially math teachers, is the personal finance bit. So by centering our curriculum in a theory, economic, Nobel Prize winning theory, and making sure it's sound in that way, it's easier for us as math educators to navigate that curriculum and know that we're doing a good job from the perspective of the personal finance, because we already have the education to know we're doing a good job as math educators. In New York City at least, a lot of the teachers who I work with and coach in my consulting, a lot of them don't use a whole curriculum. Or if they do, they're like, "Oh, I use this curriculum, but I like to teach exponents with this and logs with this, and I do this activity with this."
Math teachers are very resourceful and know the math. We don't really expect them to know the personal finance. And so trying to give them that structure and hanging the math on that we find is a really fruitful approach for combining the two topics and making it useful to math teachers. Because, I'm not expecting someone who just knows personal finance to learn all of mathematics to teach this. It's much easier, I think, to take a math teacher who already has a lot of the conceptual understanding we need ... That's why this course works because they understand the math ... and help them understand the personal finance.
Kyle Pearce: I love it. And it's so interesting. What really resonated with me, and I'm sure this came up when we spoke last ... It was a few weeks, maybe a few months ago now to be honest when we chatted, and just this piece about much of the mathematics that we teach in Algebra I and Algebra II were created or presented to solve many of the challenges, many of the struggles we have with personal finance. It's so interesting because I find regardless of if you're a math teacher or not, we in the education community are not ... and you had said there, Phillip, that you listened to the episode with Omar and Matthew ... we are not financially literate as a group. A piece you said earlier that really resonated again, you talked about collaborative learning. You talked about using context, and that's one thing that John and I, through the Math Moments work that we do, we are so huge on context and providing context.
So what better way than with financial literacy, something that everyone needs, but yet so few of us in the world actually have. So few people actually understand what is happening to your money when you're charged interest on a credit card. But, what an easy way to bring in compounding and to bring in all of these concepts into the classroom. I'm having this little mini-epiphany myself, I'm wondering can you maybe paint us a picture in the Math Moments community, a picture of ... You gave the log example. I think that's super awesome. Some people who maybe don't follow let's say the stock market, they might be like, "What do you mean if I use a logistics scale ..."
Can you paint us a picture of what a lesson might look and sound like? And, I know that for those who are listening on the podcast platforms, they only have your words but of course, for those on YouTube, if you want to share a screen, whatever works best for you, I'm wondering what would this look like and sound like if I was to go down this rabbit hole, use some of this FiCycle curriculum in order to bring these two important concepts together, mathematics and financial literacy?
Philip Dituri: Yeah, so I'll give you a couple of quick little concrete examples that I don't think I'll need visual, so if you're listening on a non-visual platform, you should be fine. Most of our retirement funds are mostly founded on the idea that if you invest in a range of companies from diverse industries, it's going to provide the least variable return. What I mean by that is I can be pretty confident that if I'm about to retire, there's not going to be drastic, drastic movement in my retirement funds and I'll have enough money to retire. In the years right before you retire, you don't care about doubling your money as much as you care about not losing all the money you've saved. You want it to keep growing, but not being destitute is more important than being a millionaire the year before you retire.
And so, that's this idea that investing in a range of companies from diverse industries usually provide the least variable return. And in fact, a question about this is one of the three questions that we usually ask populations when we're trying to measure the financial literacy of populations. The research community for financial literacy sees this as an incredibly important concept. Three questions to measure a population's financial literacy, and one of them is on this idea. So, it turns out that you can actually engage your students in some mathematical modeling to show how this works, and the only math you really need for this is to understand the binomial theorem, or to just understand what an experiment is, experimental probability and the law of large numbers.
So if you're familiar with a Galton board or if you've ever seen The Price is Right-
Kyle Pearce: Oh, yeah.
Philip Dituri: Okay, the Price is Right has a game the Plinko board, which is you drop a round ball into a series of pegs and the ball can bounce left or right on each peg. And after bouncing, it encounters another peg. And, it makes a path down this series of pegs. Well, if you're familiar with the binomial theorem, you know that that's a binomial experiment. There's a-
Kyle Pearce: Crosstalk Pascal's Triangle in there too.
Philip Dituri: Pascal's right. I love when things come full circle.
Kyle Pearce: And there it is. Crosstalk.
Jon Orr: That's it. That's the end of the episode.
Philip Dituri: Call it. No, okay. So this creates a binomial experiment and we can actually use a Galton board to model investing. So, what we do with our students is we use a digital Galton board, which allows students to set the probability that that ball falls left or right. We can set a slightly positive skew to represent the slightly positive skew of the stock market. Each of those probabilities are independent, so it's a pretty good model of investing in a range of companies from diverse industries, because what that means is that the probabilities of those stocks moving are independent of each other if they're in diverse industries. Apple and Google, if one moves, there's a chance the other one moved in the same way, but Apple and Kraft ... Maybe Apple's a bad example. Google and Kraft. If someone doesn't know Apple, they might think it's a food company.
So this idea I can set up an experiment and I can model the movement of stocks and I can run many trials. So I can say, "All right, let's see what would happen if we ran this experiment 3000 times or 200 times ..." Using a computer, it's very easy to do this very quickly. There's a lot of great tools on the web for doing it where the kids can actually watch the balls move very, very quickly. And, they enjoy this activity. It's like programming in an experiment in some sense. But what's really nice about it is that students can turn around, we can set up our model. We can explain the modeling, which is a very important standard, and then students can run that experiment, understanding the law of large numbers, understanding experimental versus theoretical probability. You can unpack that experiment so that instead of you telling students, "Listen, it's very important to invest in the range of companies from diverse industries if you want the least variable return," students can run that scenario and then turn around and say, "Empirically speaking, it seems that ..." and then say the sentence I just said.
Based on the experiment, I can see that if I invest in two stocks and I run this experiment, things changed drastically. But, if I invest in 15 stocks and run this experiment, I can see that I'm very unlikely to lose all my money and I'm not very likely to double all my money, but least variable return when I'm approaching retirement ... And, we can ask our students, "Why might you care about that approach in retirement?" Students need to understand the ideas that ... Going into that problem, they have to understand the idea that when I'm younger, I'm a little more comfortable being more risky if I think I'm might get more return. And when I'm older, I want to be less risky because the thing that made us all giggle about not wanting to be destitute the year before we retire.
So there's context for the students. It's a real world scenario. It relates to a situation we will all be in at some point in our lives. It probably relates to a situation someone they care about is in, whether it's a foster parent, a parent, a grandparent. And what's most importantly is that students can turn around and tell us the truth of it and then we can try to unpack that experience. What does this experiment mean for our investing? What is the math behind this experiment? It seems like this is the case. Can we explain it? We can run that experiment, and from that, we can try to discover the binomial theorem. We can discover some of the same discoveries, I guess, I made in my story with regards to Pascal's Triangle.
But we can make some of those discoveries. We can learn the math. The students can do it. It can be student-centered. They can tell you. You don't have to tell them. They can be the ones to discover it, and so in a sense, this model wouldn't possible. This would be a very different activity if we didn't have the context of the personal finance to make it real, to make it relevant so that instead of just playing with pegs and a ball, we're actually engaging in mathematical modeling of a real world phenomena, and that's very powerful.
Kyle Pearce: I love it. Something that pops into my mind as well is so there might be an educator thinking, "Oh, well, when I explore the binomial theorem, I usually use this scenario." And, this doesn't stop you from extending this learning to other contexts outside of financial literacy as well, which might seem obvious to say but in reality it's like, "Okay, so now how might this impact if the same player does free throws?" I think it was Darius Washington or something in that famous college game where it comes down to having to do free throws, and you could look at that through the binomial experiment. And, "Oh well, if his free throw shots are this and this ..." and show how hey, this is huge in the financial world but then I wonder maybe it's their job. What other scenarios in life does this happen?
And then, they can come back and make connections that way as well. So super powerful example. I agree that people who are listening at home did not need a visual for that one because I think you helped to paint that out in our minds really nicely. I'm wondering, and John, I don't know if you want to pitch this question, but I think this is your favorite question to ask so I'm going to let you do it ... teachers sitting at home right now wondering, "Hey, what's that first step?" What might you recommend?
Jon Orr: Yeah, that's the question that I try to pull from our guests is that you've got a teacher at home who's like, "Yeah, I want to take action. I want to bring in some of these lessons," and I think where a stumbling block might be, and I know that might be a stumbling block for even me in my classroom so I'm trying to think general for lots of teachers, is especially a first year teacher or a new-ish teacher to a department, what Kyle and I hear a lot is teachers have set curriculums given to them. So it's like, "I have to follow the department's curriculum. We've got these lessons in place. We all got to follow it. I have small maneuvers I can make on full lessons." You've been talking, Philip, about a full curriculum to cover the whole course. I'm wondering what can a teacher who's like, "I really love this idea," where can I get some resources or what can I do tomorrow to spark this, but not yet? Because maybe they're not ready yet to fully change the whole course. Where can they go? And what do you recommend?
Philip Dituri: That's a great question. Yeah, there's two big approaches. You can start small or you can just jump in. So start small. Let's start with starting small. I think you start small by incorporating financial literacy into some lessons or units where you feel comfortable doing it. I think you lean into the examples that make sense to you. You explore to see if you can find more resources out there to support you. At FiCycle, go to FiCycle.org and we actually have a bunch of free resources there for you. There's a bunch of free lessons. There's a great place to start. There's a lesson called Wealth Not Cash. That's about if you want to think about your wealth over the course of your lifetime, the most important thing is to think about your wealth and not your cash.
And students have a tendency to think that wealth is cash, so basically that lesson Wealth Not Cash, which is free on our webpage would be appropriate in many, many different settings. It's not too heavy on any one particularly math content and it introduces a lot of the basic terms. And, a lot of teachers tell me that it is very useful for orienting them to some of the vocabulary. A lot of teachers who want to incorporate this work lightly start with that lesson to give the groundwork so that later when they incorporate other aspects, there has been some touchstone experience of that moving forward.
There's other great resources out there. We have a whole series of lessons. There's another one if you're teaching compound interest. You can just pull our lesson and you could use our lesson in lieu of whatever you're doing, or in addition to whatever you're doing. I think Kyle mentioned that these activities, because they're based on math that you're already teaching, slot right in to other classrooms as well.
So, if you already have a way that you like to teach compound interest, just say, and you want to try to teach financial literacy, well I would say go ahead and do what you normally do and then try to do the lesson with the financial literacy infused. The reason I say that is ... I think this is a little bit of a tangent but just to give an example here ... I run these workshops for teachers all the time and I very seldom meet a math teacher that can calculate their 401k or the mortgage on their home. However, that's all Algebra II math. Just Algebra II. Literally the person teaching it doesn't know how to apply it and transfer that knowledge to the real world. Why on earth would their students? And so what I say to a teacher who's teaching this stuff and you're like, "Well, I don't know if I want to do the same thing with them twice," well look, most of us teachers, we know all the math we need to do our mortgage or our 401k.
And most of us would struggle to actually do that if I asked you calculate it. Your students are in the exact same boat. So if you're wanting to dip your toe in this work, you can go ahead and do a lesson. Even if you've already taught them that content, you'll be helping them with that transfer of knowledge, which we know like any math teacher who's ever had the science teacher come to them and say, "How come they don't know how to convert units or how come they don't know how to do this thing they're supposed to know," and the math teacher says, "They know how to do that." Science teacher says "No, they don't." Having a hard time transferring across the hall, it's even worse transferring out of the graduation room.
Once you've graduated and gone to college, that transfer doesn't just magically happen. So I think the first is to let go of the idea that I already taught that topic. If you're applying it to personal finance, I think it's appropriate to go at it again and help them with that knowledge transfer and show them that the math you taught them is really relevant in the real world. So, get your hands on some resources, check FiCycle.org. That's one such awesome resource. There's a link at the top, free resources for teachers where you can download a bunch of lessons.
Jon Orr: Yeah, crosstalk show notes.
Philip Dituri: The other thing I'll say is when it comes to jumping in and trying to adopt a standards aligned financial literally curriculum like FiCycle, I realize it's not completely feasible. That unfortunately the teacher isn't always the stakeholder who makes that decision. A lot of times like you mentioned, decisions get made from on high, either at the administrative level or if you're in small school, maybe the principal, maybe your department head. But, one of the things we've done to try to help ameliorate issues like that is that FiCycle is offered for free the first year. So what we found is that teachers who are really into doing this, maybe who've been tasked with teaching personal finance in their math class, by making FiCycle free the first year, those teachers can go to their principal and say, "Listen, I'd like to do this thing. It's completely free."
And, principals are much more likely to okay it if it's not going to cost any money, so that those teachers can get that training. They can get those resources. They can see how it works. Typically, we have a really amazing return rate with teachers who've taught the course for the first time. They tend to like it, so that often transfers into people working with the course. But again, removing that initial barrier of just getting in there and doing stuff. So, whether that means downloading some free resources and trying it, or whether that means adopting a curriculum and using what you can of it, I think either of those approaches are great.
But I think just doing anything to engage your students in these ideas is powerful, even just talking to them about it, talking to your students about your own experiences with personal finance and how it comes into play in your own life.
Kyle Pearce: I got to say I'm reflecting and I'm thinking too, I'm going to encourage educators who might be ... and I'm just going on a limb here thinking there might be some educators maybe a little nervous that they're like, "You know what? You just said I don't know how to calculate my mortgage, and it's true." Or, maybe I don't understand how a lot of the things in the financial world work and I'm going to send this message, and I'm sure this is going to align with your thinking as well is that through the doing of this work, you as the educator will learn probably as much as your students do. And, John and I have said this a lot about going back and trying to teach mathematics conceptually and learning about models and strategies, things that we weren't really exposed to and we never learned through our pre-service or never used during our teacher.
Now, it's like we're learning alongside our students, and I think as an educator you have to give yourself that permission to maybe not know all of the answers in financial literacy because as we mentioned, I think we're in one of those industries where in a lot of places, you have a pension already taken care of and your salary is high enough where you can go through life and not really have to worry a whole lot about these things. It can make a significant difference over time if you have a better understanding, and then you're obviously enabling your students.
The second piece I wanted to share a big takeaway is again, this importance of context. You talked about transfer of knowledge, transfer of understand. In math, we are so guilty of teaching concepts before introducing a context. The traditional way is I'm going to teach you how to do the algorithm and then we're going to problem solve later and we're going to introduce this thing, and then usually the wheels fall off. It's sounding to me a whole lot like let's take this context ... in this case it's financial literacy ... and let's bring this to the front and then we're going to let the math emerge instead of pre-teaching the math and then trying to tie in some context in order to make it work.
These are huge takeaways for me. I'm sure the Math Moment Maker audience is just full of ideas right now. They've got your website, which we'll share in the shown notes. I want to flip it back to you one last time, Phillip. If there's only one thing that a Math Moment Maker takes away from today's conversation, what are you hoping that will resonate with them beyond this conversation here today? I think it's that
Philip Dituri: It's that whole when am I going to use this in life thing. If you don't have a good answer to that question, you got to ask yourself are you trying to prepare your kids for tests or for life? And, which one's more important? I actually think that's a false dichotomy. I shouldn't say that. It's not tests or life. It should be both. So we believe that this work can have really transformative impact beyond just high school. It can impact the community. You want students informed about their financial decision making. You want them to be able to have the math as a tool to make those decisions. We want them to see the math's relevance in our life, and we think that if we do this with students by and large, and they start bringing this work into their home, we can have a real generational impact.
We didn't talk about this, but the statistics for people near retirement are not very good. At least in the United States, only a quarter of people have saved what's recommended. And, 40% of Americans before the pandemic didn't have $400 for emergency expenses, and many of them likely faced that situation during the pandemic. So, we have a problem. It shouldn't be the case that people don't understand this. It shouldn't be the case that this is knowledge that you learn outside of school. It's essential. And so, I think about what kind of generational impact is the work you are doing having? I think as teachers, we all believe that education can deliver us from a lot of the issues of our societies, that education can be an answer to a lot of problems. And, I think math is just very powerful and we're not giving students all the tools they need, or at least making clear how they can use them.
Jon Orr: True statements. Good powerful moments there for our listeners. We're going to throw your website in the show notes so people who are looking for that can find that link. But, is there anything else that you want to point our listeners to about where they could connect to you or the work that you're doing?
Philip Dituri: Yeah. So, I'm going to be presenting at this really wonderful summit. I think I'm going to be at your summit. I think by the time people hear this, it'll probably already have happened, but as I understand it-
Kyle Pearce: Yeah, we'll have that recording, though, ready for the mini academy for sure.
Philip Dituri: Check out that recording, and I'll make a promise to anyone who's listening and goes back to talk about it is I'm going to engage in the example I briefly touched on today. So that's a little Easter egg for those of you who go and watch that recording. You'll have a little connection between this and that. Also, if you're familiar with the National Council for Teachers of Mathematics, NCTM, they have a really big virtual conference coming up. We are presenting three times at that conference. We're very active in that community, so that's another great place to check us out.
And then, just to say that we are a small organization. There's four of us. We're a not for profit and we're working hard to make this a reality. So, if you're listening to this podcast and you think that what we're talking about is interesting, I'd like you to just go ahead and email me with your thoughts. Reach out. This is how we make connections. This is how we get into new schools and this is how we spread this important work. We really believe in this. And so if you do too, please don't be shy. You don't have to interact with us in passive ways. You can go ahead and email info@FiCcyle.org or just Phil@FiCycle.org if you want to reach out to me. F-I-C-Y-C-L-E.org.
Kyle Pearce: Love it. That's awesome, my friend, and we appreciate you taking the time and huge hat tip to you and your three teammates there. You are obviously a small, but mighty team. Really intrigued by the work you're doing, and anything we can do to support the work that you're doing we want to continue to do that. And, we hope to stay in touch and I'm looking forward to this Saturday at the summit, which I know this is in the past now for those who are listening, but I'm looking forward to the session and I'm sure those who are listening to this will want to dive into the academy and go check it out so they can take a deeper, closer look at some of the work that you folks are doing. So thank you, Phil, and we appreciate your time. I hope you have an awesome evening and we will see you this Saturday at the virtual summit.
Philip Dituri: Thank you both so much for having me on the cast. It was a real pleasure to chat with you both.
Jon Orr: Take care.
Kyle Pearce: As always, John and I both learn so much from these episodes. Bringing on Phil has really opened my eyes to just the idea of as mathematics becomes what we've always traditionally thought as more abstract in reality, the way that we can make it more concrete and more contextual might be through this very lens of personal finance and financial literacy. So, this has been an awesome episode. I'm excited to dive into more of the lessons that they have available on FiCycle.org. And friends, I want to make sure that this learning sticks with you so make sure that you do something to help reflect on some of the learning that you've done here today. Are you going to write a note, draw a sketch note, call a friend, have a conversation with a colleague at school? Make sure that you're doing something to reflect on so that this learning sticks.
Jon Orr: Yeah, jump over into the Make Math Moments community. The most active is our free private Facebook group, Math Moment Makers K to 12, but you can hit us up on Twitter or Instagram at Make Math Moments. Reach out to us, keep this discussion going.
Kyle Pearce: Awesome. Do us a huge favorite and hit that subscribe button if you're on Apple Podcast or on Spotify, or maybe you're on YouTube right now. Make sure you hit that subscribe button. Make sure to like the content and maybe even hit that notification bell so that you know when we release our Monday videos, which are not just these podcasts. We also have some great tips that unpack great concepts like math talks or partitive division or quotative division, or creative ways that we can lead context based, problem based lessons. So, we'll see you over on YouTube, and we want to thank you again for listening in.
Jon Orr: Yeah. Show notes and links to resources and complete transcripts from this episode and all of our past episodes are on our website. But on this episode, you can head to MakeMathMoments.com/episode164. That's MakeMathMoments.com/episode164.
Kyle Pearce: Well, until next time, Math Moment Maker friends, I'm Kyle Pierce.
Jon Orr: And I'm John Orr.
Kyle Pearce: High fives for us.
Jon Orr: And, a high five for you.
Sign up to receive email updates
Enter your name and email address below and we'll send you periodic updates about the podcast.
DOWNLOAD THE MAKE MATH MOMENTS FROM A DISTANCE CHEAT SHEETS
Download the Cheat Sheets in PDF form so you can effectively run problem based lessons from a distance!
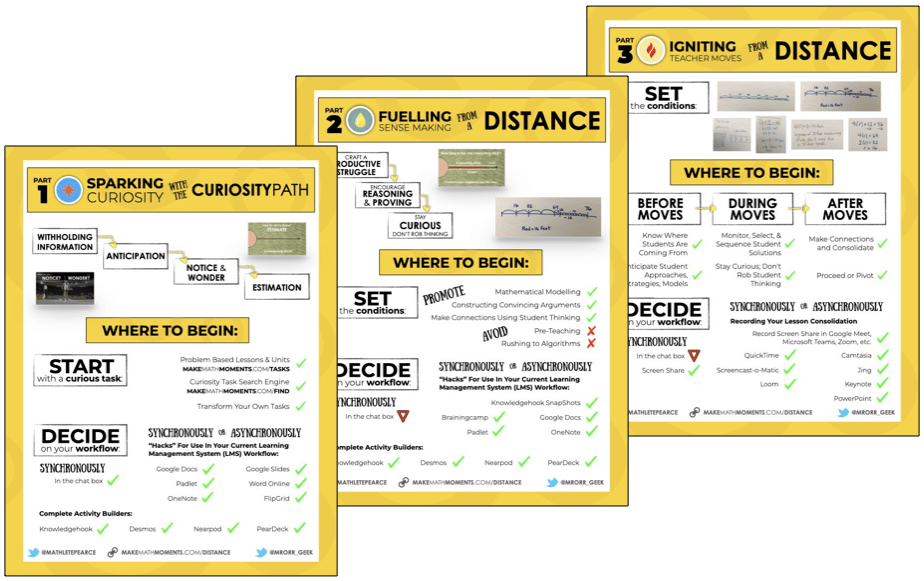
UP YOUR DISTANCE LEARNING GAME IN THE ACADEMY
There is a LOT to know, understand, and do to Make Math Moments From a Distance.
That’s why so many Math Moment Makers like YOU have joined the Academy for a month ON US!
You heard right: 30 days on us and you can cancel anytime. Dive into our distance learning course now…
Thanks For Listening
- Apply for a Math Mentoring Moment
- Leave a note in the comment section below.
- Share this show on Twitter, or Facebook.
To help out the show:
- Leave an honest review on iTunes. Your ratings and reviews really help and we read each one.
- Subscribe on iTunes, Google Play, and Spotify.
ONLINE WORKSHOP REGISTRATION
Pedagogically aligned for teachers of K through Grade 12 with content specific examples from Grades 3 through Grade 10.
In our self-paced, 12-week Online Workshop, you'll learn how to craft new and transform your current lessons to Spark Curiosity, Fuel Sense Making, and Ignite Your Teacher Moves to promote resilient problem solvers.


0 Comments