Episode 172: Avoid These Misconceptions to Teach Problem-Based Lessons With Confidence
LISTEN NOW…
WATCH NOW…
In this episode, Kyle & Jon address a few common misconceptions from the Math Moment Maker community around teaching problem-based lessons and units.
Stick around and you’ll hear how to find the right balance between what students know and what they need to learn in your lesson; when we should be assessing for learning; how to consolidate a problem-based lesson; and how to manage the flow of the class when some students complete work quicker than others.
You’ll Learn
- How to find the right balance between what students know and what they need to learn in your lesson;
- WhenI should be assessing for learning;
- How to consolidate a problem-based lesson;
- Finding the right time to teach a problem-based lesson; and,
- How to manage the flow of the class when some students complete work quicker than others.

FULL TRANSCRIPT
Kyle Pearce: In this episode, we address a few common misconceptions from the Math Moment Maker community, in particular, around teaching with problem-based math lessons.
Jon Orr: Yeah. Stick around and you will hear how to find the right balance between what students know and what they need to learn in your lesson, when we should be assessing for learning versus of learning or as learning, how to consolidate a problem-based lesson, and how to manage the flow of the class when some students complete work quicker than others. Kyle, let's do this.
Kyle Pearce: Here we go. Welcome to the Making Math Moments That Matter podcast. I'm Kyle Pearce.
Jon Orr: And I'm Jon Orr. We are from makemathmoments.com, and we are two math teachers who together, with you the community of Math Moment Makers worldwide who want to build and deliver problem-based math lessons that spark curiosity.
Kyle Pearce: Dual sense making, and ignite your teacher moves. Everybody, we are super, super excited to be able to just have this duo episode, just Jon and I, to dive into a common misconception. Not only do we receive emails from people through the website, people listening to the podcast, but some of the friends that are in our online workshops and in the academy, and even some of our colleagues when we're chatting about trying to use more problem-based approaches to learning math, and we want to get to the bottom of it, right, Jon?
Jon Orr: Yeah, totally. We do get those regular emails to say like, "Hey, I'm working with this topic. How do I address this?" Or, "This is the way my lesson went. Would you guys have any suggestions?" We get those all the time. And also you know if you're an avid listener of the podcast, this is the seventh episode you've listened to, the 10th, maybe you've listened to all of them. We know there's a couple of you out there, but you know we have Math Moment mentoring moments episodes where we chat with people, and a common thing, a common misconception that comes up, we got a couple to talk about here.
The common misconceptions, one, Kyle, being, I think people miss the purpose of teaching with a problem-based lesson. Problem-based lesson meaning the lessons that we've been talking about here on this podcast for the last few years of teaching through problems instead of teaching skills first, and those application or those tough problems later. We've been talking about teaching through problems that are very curious and very low floor, high ceiling type problem.
So I think one misconception that we're going to talk about here in this episode is like, what is the real purpose to teaching that? I think there is a little bit of misconception around that purpose and the goal. The second one is I think, Kyle, we've got lots of ... Well, not lots, but we get teachers that think, "Hey, I did this lesson, and I think it was a failure." And they explain to us why that's the failure. And then we usually go like, "No, that wasn't a failure." So there's a misconception around, again, what is happening? Like why they think their lessons are a failure, so we're going to talk about that.
And then we're going to talk about like, where do these lessons fit into the flow of things? And where do we put a problem-based lesson? And what's the best place for that? So we'll talk about those three things here in this session. Kyle, let's go.
Kyle Pearce: All right. Here we go. Jon, starting right from the top, so you've highlighted three of these misconceptions. Some people might even argue like a lot of times they're very closely linked. And I would argue that oftentimes one of these misconceptions can spiral into some of the others. So let's start right from the top. It's sort of like rethinking, maybe it's the first time you're thinking about this, but thinking and reflecting on like, what is the purpose of a problem-based lesson?
If you pause for a moment and think to yourself, why are you trying to do this work? I don't know about you, Jon, but I think many people, not everyone, I know for me, I can say this was true when I started this journey. I was looking to engage students. For me, that was it. I was sort of like, they're not really paying attention. When I say they, I'm talking about a good chunk of my class. You have this group of students who they're going to do whatever it is that you say, just because that's just who they are as students, and they want to get their stuff done and so on and so forth.
But even just looking at the expression on their face, oftentimes they're not maybe enjoying the process. So we were looking for engagement. I would argue that problem-based lessons can help you do that. But oftentimes things fall apart a little bit if that's our only intent for a problem-based lesson. And I can say pretty confidently that both Jon and I, our purpose of building a problem-based lesson now is a lot different than back when we first began. A lot of times people confuse their goal to see if students could do what we've already taught them. So-
Jon Orr: Like the tough problem. Yeah. Like it was like, yesterday I introduced solving equations using ... Two steps for solving equations, and I showed how to do the balance method, or maybe you said, we subtract this on this side, you showed them opposite operations. However you taught it-
Kyle Pearce: The formula, whatever the formulas that you're working with.
Jon Orr: Right. You went through some examples. This is the way I used to do it. And then either you saved this problem that you're like, I got a good, tough challenge problem for them. Or when you first got into it, it was like-
Kyle Pearce: And it's engaging crosstalk.
Jon Orr: Yeah, this very curious, engaging problem. I'll see how they do on it tomorrow. So I taught them all these skills today, and I'm going to use that tomorrow and see if they can step up or rise to the challenge, and see if they can piece together and apply their learning to solve that particular curious problem. Maybe it started with video, maybe it didn't. Maybe it just had this curious low floor entry point, and it did have a high ceiling, but we're going to leave it to the next day, and not start on that day, because I definitely did that, Kyle. I started teaching problems that way using them as these engagement pieces, but only after I taught everything upfront.
Kyle Pearce: Yeah. Absolutely. And for us now, we look at it actually quite differently. I was co-planning with a teacher in my district recently, and this teacher is super eager to bring in problem-based lessons into her curriculum. And that's fantastic. That's awesome. I'm going to say naturally, because for me it was naturally, this is how I did it. I know Jon, you did the same, was like, I looked at what I was already doing, so I looked at how I had my course structured, my program, and then I would just drop these problems in.
And typically, like you said, I would drop them in after I did some teaching, because, remember, the kids haven't been taught how to do it yet. That was my thought. That was my thinking. Again, you're not wrong for thinking this, if you're going, well, isn't this what we're supposed to do? And over time what we realized was, hmm, okay, maybe the problem was a little more engaging, but the reality was, is like, I still got a lot of the same that I would've gotten regardless of what problem I gave those students.
What I mean by that is if let's say I was teaching circumference of a circle, or maybe the area of a circle, or whatever, circle measurement, and I teach them the formula for circumference. I teach them what pie is. Even back then, I'll be honest and say like, I said what pie was, but I didn't let them experience what pie was. And then I give them the area formula. And then I would give them a problem like my cookie cutter problem that I had done over 10 years ago, I think it was, when I did cookie cutter. It was to drop in to my unit for circle measurement. I was like, all right, they're ready for it now.
Now we drop that problem in, and sure they were engaged in the notice and wonder. We didn't have the curiosity path mapped out for ourselves yet. I'm sure it could have been way better than what we were doing at the time, but it was an improvement for my class. And then what I would get though was a lot of the same. I'd get the same students who could do the problem as before, I did this type of lesson, and the same students who weren't really willing to take a chance or take a risk.
What we realized later was by doing this, it's like students know that they're supposed to know what to do. Like if they don't know what the next step is, they're like, I'm going to just opt out, and I'm going to wait for Sandy over there to do it. Because like, I know she'll know what to do, but I don't know what to do, and I should know what to do by now, right?
Jon Orr: Yeah. You bring up a really great point, because I've experienced this totally when you regularly don't engage your students in that thinking process first, and they're left to be like, I'm supposed to follow along in this kind of process, and if I don't know how to ... If I've not experienced diving into a problem and not knowing how to do it, they will hold back and wait for the kids who may have participated more often in class to solve it first than diving out. I've definitely experienced that in my class when I pre-teach things.
Kyle Pearce: Yeah. Absolutely. It was kind of like, when you zoomed out, I felt like I doing a lot more work because it was ... I was trying to teach two different styles of teaching, kids were all like, which one are we doing here? Are we doing this or doing that? And I got a lot of students who would just be like, can you just tell us the formula? We'd get a lot of those things.
What we realized was this is actually the goal for us is not to test students on whether they could apply what I already taught or not. It's actually looking at it from this opportunity to introduce students to new learning. It was almost like we weren't doing problem-based lessons, we were doing contextual practice. We were doing curious practice, which, not bad. I mean-
Jon Orr: Yeah, you were applying learning, which you had to pre-taught. That's part of the work that we have to do is that we do have to apply our learning in different situations, but for us, right, Kyle, for us, the purpose of the problem-based lesson, for us, isn't that can I apply the memorization tools I've already put in place on a new situation. For us, we want to engage our students in a new situation that they don't know how to solve right off the bat, and we want to get them thinking and see strategies that we can emerge to get towards a learning goal.
Kyle Pearce: Again, I just want to be very clear on what Jon just said. We still need the problem to be accessible, but maybe not with this new tool that we're hoping, or this new strategy, or this new thinking that we're hoping to emerge. So it's kind of like thinking about it different. Like, okay, I don't want to use a curious real world. I'm using little bunny ears for those on YouTube watching Real-World or 3 Act Math. Whatever the type of problem that you're using, it's not for practice, it's actually to introduce new learning. It's actually to introduce students for the opportunity to think, and to almost prime their brains for this new learning that we're going to do.
Jon, I think that's kind of like, we're going to continue this conversation, but I think it's a nice segue into what we were going to talk about where we get a lot of teachers that come back to us and they say, I tried this lesson over here. Like someone recently told us like the wooly worm race is what they tried. And they were like, "I think it was a total failure." And then we went on to read it, and you and I were sort of like, "Actually that doesn't sound like a failure at all." Right?
Jon Orr: Yeah. And we get an email like that, or we talk to another teacher like that. I think what's happening, and this is that misconception piece is that the teacher has missed the idea of a particular goal that can be great. And I think if you're using your problem-based lesson to practice, that's a different goal. I think people can do that, but I think there's a much deeper and richer experience for you in your class if you do use it at the beginning of say a topic to emerge ideas and bring about those ideas.
And I think this teacher that was emailing us actually was doing that. They were not using this task to practice in hoping that the kids got it and they think it's a failure there. They're going, okay, I'm on board guys. I want to use a problem lesson to introduce an idea with my students. I think the misconception when they thought it was a failure was the idea that even though I haven't taught this skill, they think if by just using this problem-based lesson, kids will naturally show me that skill.
And I think there's a misconception right there. It's not all of a sudden my kids are going to be solving two step equations just because I'm using this task, or my kids aren't applying or building a linear equation because it's a linear relation, not a nonlinear relation, just because I'm using this engaging task.
There's a lot more nuance that has to happen on the teacher to bring about those. That's why the teacher, I think thought it was a failure, because they expected all of a sudden to use this task and kids to all of a sudden show these skills and go, "Hey, look, I just taught this lesson. I got my learning goal out, but, wait, the kids didn't do it, so it's a failure."
Kyle Pearce: Yeah. Totally. And in particular, this particular email was saying like a group of students were good, and with wooly worm, for those who haven't tried that unit, it's about representing and comparing fractions, we're using essentially like a linear model, but it's more of like a bar or a tape diagram that we're getting towards this linear model.
And some of the students were unable to represent some of the fractions, which then obviously hindered their ability to compare the fractions. Like the big idea for this unit is all about representing fractions and comparing fractions, and some of the students were unable to do that. And this is where we've mentioned this before on the podcast, but I think it can be missed very easily is that we want to use these problem-based lessons as like assessment machines, but not necessarily like summative assessment machines or even, I would say, formative assessment, yes, but almost more diagnostic in a way.
Because if you think about it, it's like, okay, I'm introducing this idea of representing and comparing fractions with my students. The reality is, is that students, unless you're teaching kindergarten, it's likely that students have had to represent and compare fractions in some way, shape or form. Whether they were proficient with it or not is another story. But it's not like brand new, out of the bag. They'd likely know, "Hey, this is what a fraction is and we can explore fractions."
But now this teacher basically did this problem-based lesson, something that all the students can access. And then by the time they were ready to enter into the consolidation of the lesson, they knew so much about their students, and where they were, which is essentially the goal. Because now we walk into the consolidation going, "All right, this is what we're going to talk about in the consolidation, based on what I saw from this group or that group or this student or that student." You actually get to look at that and go, "Here is what we are going to dig into today in order to take our next step."
It wasn't supposed to just magically happen on its own. Of course, as you're going around the room or if you're teaching virtually, you want to be prompting students, you want to be probing students, you want to be asking questions to nudge them along. But the goal isn't necessarily that everybody's a level four here in Ontario or an A+ comparing fractions student. It's the beginning of the learning journey. And now you know so much about each of your students, and that can impact where we go next, both in this lesson and the remainder of the unit.
Jon Orr: Yeah. And in these days, the more and more I use our problem-based lessons to teach my students, I always think of two goals almost in my lessons. I do have an end goal. I do have a learning goal that I want to bring about. Maybe it's a particular strategy, maybe it's a way to look at a relationship this way, maybe we're solving two step equations. I've been using that example today, but the other goal is, like you said, I want to see what we know first.
And that is, it's almost like three birds, one stone, Kyle, because I'm going to emerge that learning goal. I'm going to see where my students are, and they were all engaged in learning and thinking, instead of just copying stuff down and not thinking. Think of all the three benefits you get there when you start with a problem-based lesson, and you didn't pre-teach everything is you get to see where your students are. They are thinking along the way and using prior knowledge or past ideas that they've had, and they're using their brains, they're communicating with each other, and you get to bring out that learning goal at the end of the lesson.
Kyle Pearce: Yeah. I love it. The last thing we wanted to talk about is this idea that a problem-based lesson, it's not a standalone. If it is a standalone, then you lose some of that benefit you just referenced, Jon. If I look at it as just something I plop in there randomly, I don't think you're going to get that same benefit, but I want to go back to like, think this wooly worm scenario.
So this particular educator who's constantly reflecting on their practice, they try this, and then now it's like, okay, I've got out my next steps for my consolidation on what I really want to spend the time on. Think of how I used to teach and the way you used to teach Jon was like, today, I'm going to talk about this, this, this, this and this, even though I have no idea whether everybody knows it, or whether they're ready for it. I mean, that might be a little farfetched. I know somewhat where students are, but if it's a brand new concept, there could be like three of these five things might be something students are pretty strong with, and I could spend more time on these two.
So this teacher now goes, okay, this is what I need to spend some time on in the consolidation. The reality though is in that class and in this particular teacher's response to us, they said, "I had some students that were successful, and then I had some students who were stuck." So it's like, okay, you've got to pick some of that student work to help bridge that gap and show the connections, but then guess what? I can give them a consolidation prompt.
Like for tonight, let's say, like one question, just to get them thinking. It might be two different questions. One for some of these students who are comfortable with representing those fractions. So maybe it's more on comparing. And maybe for this group, it's more on like, hey, we need practice partitioning our holes so that you can make sixths and eighths and fifths and some of these other ones that students were struggling with this particular teacher.
But then the next day doesn't necessarily have to be a brand new lesson. It doesn't have to be a new problem-based lesson. It might be what we call, like on day two of many of our units is usually a purposeful practice day. We usually start with a mini lesson of some type. Essentially we'll build on the previous day's concept, or context, usually just verbally. So we just say the context.
We give them an opportunity to reiterate the idea that we were trying to draw out, gives students the opportunity to build fluency and flexibility with this idea. It allows me to then kind of go, okay, yesterday I had these students who are really feeling good, these students who are struggling, where am I now at the end of this math talk, at the end of this mini lesson that we're going to do here as a group.
And then I can send them off to do some practice problems, which, surprise, they're not necessarily engaging because it's practice. I don't need to engage them for practice. It's like, no. Now you know what it is we're after, let's now work on this, and maybe I can pull a small group, or I can make an excuse to go talk to these three students so that I can address specifically something that they missed.
But really it's like we're building off the problem-based lesson to do the deeper learning. And to really, you can call it remediate, in some cases, but it's like push students further and accelerate their learning, whether they got it yesterday, push them to the next point, or whether they were struggling with that idea, give them an opportunity to try to accelerate their thinking as well. It's not disconnected, and it wasn't like one and done, and then tomorrow we start teaching them something to get them ready for the next problem-based lesson.
It's like, no, we're going to practice. We're going to get better at what we did yesterday. And, hey, I'm going to even challenge you. Yesterday I saw this model, or I saw this strategy, I wonder, how about in this scenario? I want to challenge you to try this strategy if you didn't try it yesterday or try that strategy, if you didn't try it yesterday. So everyone has something to work towards, and we're seeing this progress.
And when students see that fluency and flexibility start to build, their confidence starts to rise, and then they become more brave. They become more vulnerable to actually stick their head out a little bit, or stick their neck out and go, "I'm actually going to engage in this problem because they weren't expected to know the best way to solve the problem in the first place."
Jon Orr: Yeah. That's a great point. And I did want to bring that up about the confidence students do get when they are continually being asked to think first, and then you're responding to them. So that's such a great confidence booster when we teach this. So another added benefit here, which is what we're trying to do. We're trying to get students to be confident, to be fluent in mathematics. And you can't do that, doing this way of leaving the problem-based lesson as a drop in.
Kyle, you've said it before that we're trying to build our unit around a problem-based lesson, instead of fit that problem-based lesson into our unit. It's kind of a backwards kind of approach here than our traditional approach to bidding in these tougher problems, is we start with that problem, and then we build our unit around that.
Just wanted to address something on timing. I know that sometimes we say, and it depends on the time you have with your students, because you said day two might be a math talk, and then a purposeful practice. And it depends on how many minutes you have in your math block. It's also possible, and I'm cutting myself off here, because it's definitely possible, based off the topic or the problem-based lesson that you're working with, that you in your first part of your lesson, you do all these things and you consolidate.
And then in the second part of your lesson, that could be also a purposeful practice piece, depending on how many minutes you have. Because I know that a lot of times in my class, I can fit both of those pieces into one day with my kids on my math block, so in that particular class. I think it's such a great thing about building your unit around a problem-based lesson. And I know that we've been doing that. We have many lessons, as in problem-based lessons on our website. However, there are many units built around those lessons.
And so we usually have five day units or six day units or a four day unit that kind of take that approach of introducing through the problem-based lesson, a purposeful practice, then extending a little bit more into a new extension idea, and then another purposeful practice or math talk. We've got those full lessons, full units for you to access over at makemathmoments.com/tasks, which is where we house our catalog of units and tasks, lessons for you to use. We've had a, Kyle, last month, at the time of this recording last month, we did a full webinar series on transforming a textbook into these types of tasks.
And I know that some of the folks were saying like, we went through the course, we went through that webinar series with you guys live. It was a great experience, but it's sometimes time consuming to think about transforming those lessons. And a lot of times I say, yeah, it is. We are just super geeks, and that's why we want to do it. And that's why we've built the library for other folks to use our lessons if you can fit one in, instead of remaking one of yours. But we just wanted to show how we've remade ours in that series.
Kyle, let's do a quick recap here. I want to recap the three misconceptions we've talked about here. I'm just going to do them in the order we did talk about them. We talked about misconception being the purpose of using a problem-based lesson. We spun that around to say, "Hey, we're purposely choosing this to introduce ideas, not to practice ideas later," so that this idea of, what is the purpose? Is a common misconception.
The second one we talked about here was addressing the idea that many teachers think their lessons are failures because students didn't show them the strategy that they thought the lesson was supposed to bring about. We talked about how to think or readjust your thinking around that idea, because you are bringing up to merge ideas, and then there we can connect dots afterwards. And the last one here we just talked about here is this idea of this problem-based lesson being a standalone approach. We want to build our units around that particular lesson, and not the other way around.
Kyle Pearce: I love it. And friends, of course, if you are thinking about doing problem-based lessons and you need a little bit of support, of course, reach out to us. We love hearing from friends comment on the blog or on the YouTube channel, and we'll do our best to help support. But ultimately at the end of the day, I would say, if you're new on this journey, or maybe you've been on this journey, and you're still feeling like you're like, ah, it's just not where you want it to be, go and try one of those problem-based units.
And I would argue, look at the entire unit before you dig in. Just have a look. Kind of plan, what does it look like? Something we didn't mention here, we won't dig into it too much, but some people say, well, you said day two. Does it have to be day two? And it's like, no, of course not. Your block is going to be a different time, length, and maybe it might look a little bit different. But what I would suggest though is try not to skipping over things, at least try a unit, try to use like a good amount of each one, especially those math talks, because I'm telling you, those math talks are designed in a way that will help you build that fluency and flexibility.
The thing we always say we want our students to have, but yet it seems we never have enough time to do it. And I think we need to make that time. So I would really encourage you. That's one thing I would say, go try one and actually give it a really good shot. Don't just pluck out the problem-based lessons. Because like Jon said, day one and oftentimes day three, somewhere in the middle of the unit, we'll have another problem-based. You just do those two. Like you're going to be stuck with some of these same misconceptions we chatted about.
Hopefully you found this helpful. I know for us, the more we talk about it, the more we organize our thinking and how we might go about teaching the next lesson when we're in the classroom. We want to thank the Math Moment Maker community for hanging out with us as always. And friends, what are you going to do in order to reflect on what we chatted about here today?
A good idea might be to write it down. We talked about three misconceptions. Go write them down. If you're a sketch noter, get out there and start sketching it down, or go and tweet it, or throw it in our Facebook group, Math Moment Makers K-12. Whatever you do, make sure that you're doing something so that this time, this investment that you're making to listen to the podcast will pay the highest dividends that you possibly can.
Jon Orr: Good tips. In order to ensure you don't miss out on new episodes of this podcast as they come out each week, be sure to subscribe on your favorite podcast platform. Also, don't forget to jump over to YouTube, and subscribe to us over there. We are putting also weekly videos out, not necessarily this video that you're listening to right now, we've got new weekly, smaller chunk videos on how to do things. We've got a series on how to teach algebra in a visual way.
Kyle has a whole playlist on how, or classroom sneak peeks. So specifically we were talking about running a problem-based lesson and what that might look like. We got a full sneak peek that Kyle used with a class he taught not long ago. So you can get a sense of what that might look like and sound like. So head on over to YouTube and subscribe over there as well.
Kyle Pearce: Awesome stuff. Show notes and links to resources from this episode, as well as all the other episodes can be found over on the website. But for today's episode, head over to makemathmoments.com/episode172. Holy smokes, we've got lots of episodes going here. Again, that's makemathmoments.com/episode172. Well, until next time Math Moment Makers, I'm Kyle Pierce.
Jon Orr: And I'm Jon Orr.
Kyle Pearce: Hi fives for us, and high five for you.
Sign up to receive email updates
Enter your name and email address below and we'll send you periodic updates about the podcast.
DOWNLOAD THE MAKE MATH MOMENTS FROM A DISTANCE CHEAT SHEETS
Download the Cheat Sheets in PDF form so you can effectively run problem based lessons from a distance!
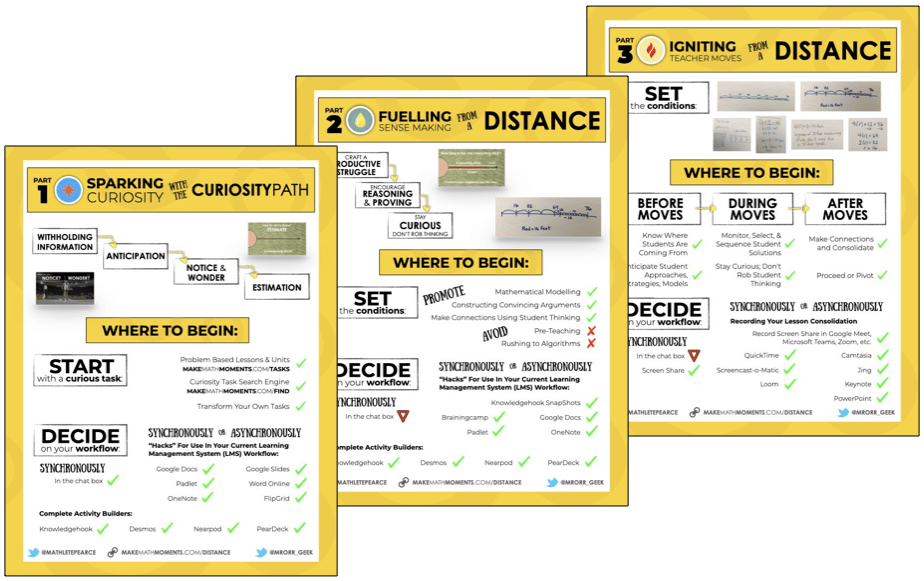
UP YOUR DISTANCE LEARNING GAME IN THE ACADEMY
There is a LOT to know, understand, and do to Make Math Moments From a Distance.
That’s why so many Math Moment Makers like YOU have joined the Academy for a month ON US!
You heard right: 30 days on us and you can cancel anytime. Dive into our distance learning course now…
Thanks For Listening
- Apply for a Math Mentoring Moment
- Leave a note in the comment section below.
- Share this show on Twitter, or Facebook.
To help out the show:
- Leave an honest review on iTunes. Your ratings and reviews really help and we read each one.
- Subscribe on iTunes, Google Play, and Spotify.
ONLINE WORKSHOP REGISTRATION
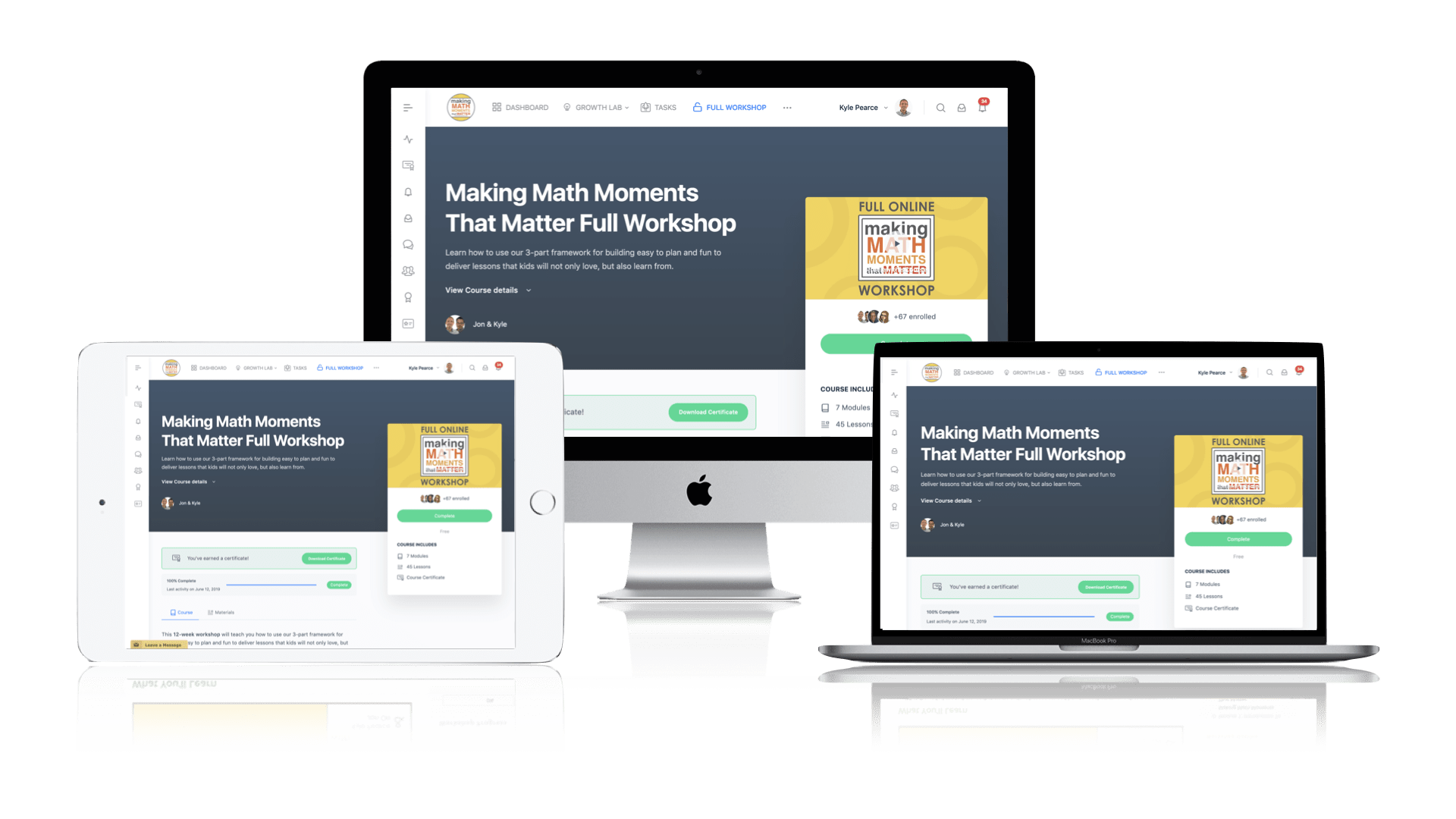
Pedagogically aligned for teachers of K through Grade 12 with content specific examples from Grades 3 through Grade 10.
In our self-paced, 12-week Online Workshop, you'll learn how to craft new and transform your current lessons to Spark Curiosity, Fuel Sense Making, and Ignite Your Teacher Moves to promote resilient problem solvers.


0 Comments