Episode 196 – What’s After The Lesson?
LISTEN NOW…
WATCH NOW…
What do I do after I finish a lesson? How does practice fit in? Do I have enough time to build conceptual understanding using a problem-based lesson AND still build fluency?
In this episode Kyle and Jon share how they design lessons to meet these common “pebbles in our shoes” and while still covering the content standards.
You’ll Learn
- How to teach through problem based lessons with intentionality;
- What the most important learning target for any lesson should be;
- How and when to use math talks in your unit planning; and,
- How and when to use practice in your lesson/unit planning.
Resources
Courses:
How To Transform Your Textbook Into A Curiosity Machine [Free Video Course]
Classroom Resources:
Make Math Moments Framework [Blog Article]
Make Math Moments Problem-Based Lessons & Units
Podcast Episodes:
Why Use Math Talks and How To Ensure They Are Effective [Podcast]
What’s on Your Worksheet? [Podcast]
Are you a district mathematics leader interested in crafting a mathematics professional learning plan that will transform your district mathematics program forever? Book a time to chat with us!

FULL TRANSCRIPT
Kyle Pearce: Welcome to the Making Math Moments That Matter Podcast. I'm Kyle Pearce.
Jon Orr: And I'm Jon Orr. We are from makemathmoments.com and we are two math teachers who together-
Kyle Pearce: With you, the community of math moment makers worldwide, who want to build and deliver math lessons that spark curiosity-
Jon Orr: Fuel sense making.
Kyle Pearce: And ignite your teacher moves. Welcome my friends to another Making Math Moments That Matter Podcast episode where you're going to be hanging out with both Jon and I. And today, I'm pretty excited for our topic right here, Jon? What are we going to be chatting about?
Jon Orr: Yeah. What we're talking about is a common wonder, a common question we get from our academy members, from listeners like you, from teachers that we talk with on a regular basis, from our districts that we work with on a regular basis is the question about, "Okay, I've done this problem based lesson. You guys gave me some resources, or I learned some resources on how to get my students up and thinking first and interacting with models and strategies we've chosen for a particular problem based lesson. We're getting our students to be more engaged through noticing and wondering. And I've got to the point where I've connected, I've consolidated. We've brought the big idea of this problem based lesson out. And then I feel like I've wrapped it up. We've wrapped it up in a nice bow and we've related the learning goal to it. And it's like, I'm done that lesson." And then the question becomes now what? And a lot of times now what for teachers are really asking the question about, "Now, what do I do with practice? Where does practice fit into that problem based lesson that I just did? Or maybe there's something else I'm supposed to do to help with that practice. What is the next thing to do once I've completed this wrapping up stage of the learning goal of this conceptual lesson that I just finished?"
Kyle Pearce: And I think really there's maybe this misconception or maybe just this idea in people's minds that because you and I are trying to shift the learning process ... We'll call it the beginning of the learning journey for some new ideas, these new big ideas that we want to emerge. That that's all we do in our math class. People in their minds have this vision as though it's like, okay, if I go into Jon's class, what I'm going to see is him doing problem based lessons that look very three act in the beginning, then he does five practices to consolidate and then it's like everyone leaves. And then tomorrow we do it all over again.
Jon Orr: We do the same thing.
Kyle Pearce: And that's it. And there's never anything else. And we've said it many times on the podcast that that's actually not the case. We tend to use this idea as a means to introduce things, to bring in a new idea, this big idea, to emerge strategies, to emerge models. And that there's actually a whole lot of other work that has to be done in between. We just don't spend as much time talking about those ones because to be honest, I don't think it's where teachers struggle the most. I think it's with problem based lessons, which is why we focus our ideas on that.
So really the big idea that we're hoping to unpack here today is that the problem based lesson we think is a really important and critical part of not only building students' confidence, problem solving skills and their resilience, really that overall productive disposition in math class, but also that we want to take this idea and we want to use it as a way or as a means for students to build procedural fluency. So again, we're saying it once again that it's not an either or. We want them to conceptualize what's going on, but then we want to use that.
The reason we want to do that is so that students can build and develop the fluency so that they don't have to spend as much time thinking about things. Eventually certain ideas will become second nature almost to the point where they're like, they don't even think about them anymore. We certainly want to push them to think about them every so often. Bring them back and make sure they don't forget why things are working the way they are. But we want them to learn about the behaviors of mathematics. So it isn't the only part. The problem based lesson isn't the only part of our math program and today we're going to unpack specifically what we are going to do after that introduction, after that emergence of a big idea, a strategy or a model comes through our problem based lesson.
Jon Orr: Yeah. So we're excited to dive into that piece of math class with you here in this particular episode. But if we relate this to many other things, this idea of understanding what you want to learn conceptually, and then practicing that, and then always this loop of coming back to this conceptual understanding, practice, conceptual understanding, practice is so important in learning a particular skill or a particular understanding for many things. We've talked lots about, say the hero's journey on the model of learning these skills in your life. On feeling like a productive struggle. Battling against the forces of evil so that you attach value to new learning. But that conceptual understanding is happening in that piece but then that practice has to come back and reinforce the conceptual understanding. So if you're thinking about playing a sport or playing a piece of music on a new instrument, you're constantly going through that.
I have to understand how the chords fit together in music, or if I do, then I'm in a better position to understand music and make music instead of just memorizing where chords go on my guitar. But then once I know how a core progression fits together, then I can then practice and practice and practice so that I can get good, but then recycle back to going, okay, how does that fit in with my ideas of where the chords go together? That's really important for music. But Kyle, I know that you're hard into baseball right now with your son playing little league baseball. And I know that you've been thinking about that idea too. I think most people listening know that practicing a sport is so important, but let's tie that back to this understanding of a piece of the game.
Kyle Pearce: I love that. And actually, I just wanted to comment too on your music example is just this idea that it's not a one then the other. It's not all conceptual, then all procedural. You mentioned this idea that as you are practicing, you are coming back to the conceptual. You're constantly iterating through these things, almost like a cycle. As you learn something new with the guitar, you're thinking like you had mentioned, where does it fit? How does it belong?
And the same is true with sports. The idea that just popped into my mind this morning as we were chit chatting and hit the record button here was just our last baseball practice. My son's been playing a lot of ball this summer and he's really enjoying it. And the whole team has come together and they've all done a ton of growing. He's an eight year old, late starter to baseball as are many on this team. And we were trying or practicing or introducing, I should say ... I shouldn't say practicing yet because we were actually introducing ... Picture the problem based lesson in my math class. This would be the problem based lesson in my baseball practice where we were saying, "Wow. When that ball gets hit into the outfield and that outfielder is running way out there to get the ball, we're in a tight spot." So we're asking students in a circle, just talking, how can we help that outfielder out? What do you think we should do? So now think of how that works in a math class. We are always asking questions. We're asking them to conceptualize what's going on. And of course the baseball players are all saying, "Well, they're not going to be able to throw the ball in from there. They don't have a big enough arm to throw all the way. But they could run it all the way in."
But if they're running all the way from outfield ... I'm like, "That's a great idea. It would work. But I'm wondering what's happening to the base runner as you are running? The base runner's running. So that's not a good thing. How could we get that ball in?" So you think about just in that scenario, that is what we're doing in a problem based lesson. We are trying to put students in a position where they can bring ideas to the table. We're not saying if they say, hey, we're going to run it in. We're not going to just practice that strategy all day long. We're going to value it, we're going to move on from there and we're going to try to emerge a new idea. This idea of the cutoff person.
We need a player to run out there, halfway between the outfielder with the ball and the second base so that we can do a relay throw all the way in. So in that moment, we are helping them, students in this case, the students of baseball, to understand, to conceptualize this idea. This big idea that we want to emerge called the cutoff. And at that point, we're not just going to be like, "All right, great job. Make sure to do that in the game on Saturday." Right Jon? We're going to go, "No. We need to do some practicing of that." And of course that practice is going to be very slow and intentional at first and then we're going to eventually start speeding it up. We're going to throw in variables. We're not going to hit the ball right to the outfielder this time. Now we're going to send one way deep or we're going to send it into left center.
What's going to happen now? Which player's supposed to run and do the cutoff now? Is it the shortstop or is it the second basement? Who's closest to the ball? Oh, this shortstop. Okay. You run out to left center and help run that cutoff. So in my mind, I'm just helping people to see from we've got this problem based lesson happening where there's lots of conceptualizing, but there's also this reflecting, this opportunity for some practice, but then we're not just moving along and never coming back to it. We now practice some cutoffs in some way, shape or for at every practice since we've introduced it. Very intentionally.
And we find very fast, meaningful ways, not that they have to do it fast, but fast ways that we can integrate it into our practice routine so that we can get a little bit of practice in there and we also try to introduce some new conceptualizing as we go. So that iterative practice is taking place. So my wonder there, Jon, is how do we bring this idea back to our math classroom? Let's actually give an actual math example of maybe a concept and how we might be able to frame this from the problem based lesson to what do we do next after that? Because again, that's the question we want to really address here. What are we going to do with our students and what's that format going to look like?
Jon Orr: Exactly. Exactly. So we'll use an example here to walk through from one of the problem based lessons that we've used it in our classrooms all around scaling ratios in this example. But I do want to put a caveat here that we're not going to go deep into the mechanics of the problem based lesson first, because we've done that here on the podcast many, many times. Almost all the episodes that we talk about here go into that. We want to focus a little bit more on the next step. But we do want to frame what this looks like and sounds like in the context of the problem based lesson, because when we're thinking about our problem based lesson, we're really following our three part framework here at Make Math Moments and everything that we do is following this framework on thinking about how do I spark curiosity in a particular lesson? How do I get sense making? Which is really the most important part of these lessons that we're trying to get. This is the part that we're trying to get kids to use strategies and models to make connections. That's the conceptual understanding part so that we can move into the building of procedural fluency, which is that next step.
So we want to make sure those two pieces of the framework are accounted for. And then the third part of our framework is the moves that you're making as a teacher to make all of that happen. But when we start with a problem based lesson that we're going to showcase ... Kyle's on the screen right now. If you're watching over on YouTube, he's showing some pieces of our problem based lessons that we've made that we've used in our classrooms. But I think we want to reiterate something that we've talked about many times here on the podcast and actually helped many teachers in our mentoring moment episodes with is thinking that first piece about the problem that you're going to work with your students, which is all about intentionality.
And I think that's going to carry forward into our purposeful practice piece. What's the next piece we do after this? It still carries forward this intentionality of what you want. And I think the intentionality piece we should talk about here is what big strategy or ideas do you want to emerge from this particular lesson? And I think it's deeper. We've talked about it, but it may be not very explicit as we always should be. But I want to be explicit about the intentionality when you're choosing a problem based lesson. So for me, a high school teacher or a middle school teacher, the intentionality isn't just the topic for us. It's not just like, "Hey, I'm going to solve two step equations or I'm going to compare ratios." It's not that general. Even though your textbook on 2.2, it says that. When you say, "Oh, I'm okay. I have my intentionality. I'm solving two-step equations." But we know it has to be a little bit deeper and more specific than that for this problem based lesson to work to build conceptual understanding.
So for example, it might be solving two-step equations, but you also have to add another sentence on there to say, I'm going to solve two-step equations with what strategy and what model? That's an important aspect because you're trying to give kids this conceptual understanding of solving two step equations, but we want to do that through models and strategies so that they can use them to do the work that you're going to do in the purposeful practice and they're going to make those connections for prior models that they've learned along the way. So just grabbing a task and going, "Hey, I'm going to solve two step equations," isn't good enough. We want to think about the intentionality and then that's really going to help you do that next step.
So if you focus in on that, then once your problem based lesson is over, when you move to your purposeful practice or whatever you're going to do next, which we are going to talk about, you have that intentionality that has to follow. That same thing comes along the way. So I wanted to make that part clear so that when we get there, we don't forget that part. And I think a lot of times that's happens. It's like, "Oh, I just did this great lesson. I did this lesson where my kids were up. They were thinking. They were engaged." And now I'm going to move into my practice part, which is what I think might come next. And then I've just thrown the worksheet in or I've just ... Let me just grab some questions from the textbook and I think they're going to make that transition into that practice problem instead of thinking about more intentionality around what questions am I choosing so that I can continue the work around the models and the strategies. So we'll get into that a little bit more, but let's keep going Kyle with some pieces around selecting and working through the problem based lesson first.
Kyle Pearce: Yeah, absolutely. And the point that really you just drove home for me was, when we just give students practice without making the intentionality clear to the students ... Because again, we might have intentionality. We may have picked those problems for a specific reason, but if we're not helping to guide students to understand why we are giving them those particular problems to practice, they might miss it. And then it becomes, again, this get done subject we've talked about before. It's like, okay, I just got to get through these. But it's like, no, listen today ... So up on the screen for those who are on YouTube with us right now, I'm in the actual teacher's guide on day one, just to set the intentionality for what we would be doing on day one. And then also what that might look like on day two and beyond as we get into the purposeful practice.
So with this particular problem called planting flowers, it's all about ratios. And in particular, some people look at things and sometimes they look at the problem on day one and they think, "That problem doesn't feel hard enough." But if you look at the intentionality, we've designed it in such a way that we can emerge this big idea, the strategies and the models specifically, and we can highlight them to students so that they learn the behaviors of how these work. So today we're looking at ratios. In particular, composed unit ratios. And for those who are unaware, we talk a lot about it in our course called The Concept Holding Your Students Back. I didn't realize this as I was teaching for over a decade. I did not realize that there were different types of ratios. I just thought a ratio's a ratio and a rate's a rate.
But when we're dealing with a ratio where there's two or more units being compared, we can call it a composed unit. It's like they scale together. They're glued at the hip. And today we're talking about flowers and flower boxes or pots. Whatever you want to think of them as. So the visual has these flower boxes. So we're comparing how many boxes, how many flowers. And these go together at the hip. And what we're trying to show students in this lesson is that we can scale a composed unit ratio in tandem to reveal an infinite number of equivalent ratios. So some people might be thinking about that and going, "Okay, that makes sense. I can scale any ratio up or down. Awesome." But in particular, we can reveal the rate through this particular action. When we go down and we find the ratio of something to one or one to something, we can see the rate there. We can see it emerged.
And this is something that will help students every time they see division later. They go, "Wait a second. If I'm seeing division, which is a particular positive division, I can actually use this strategy." And the model we're trying to emerge through this series is the double number line. So up on the screen, you'll notice in the teacher's guide, there are different student approaches you might see students using. So you might see students physically dividing the flowers into different groups like fair sharing. That's what partitive division is. So that's students who are just entering into this idea, all the way to a student who might have some experience with a double number line or maybe a bar model. This bar model might be a great one for us to look at. This scenario gives us ... I believe it is 72 ... Or sorry, what was it? 72 flowers and four boxes.
And this student basically scaled all the way down to figure out that there's 18 for every box. So you can see this rate emerging here. And later in the problem, we figure out how many we need for six boxes in the backyard so they can scale up from there. So you see this model and basically what we're trying to help students see here is that, wow, anytime we have a composed unit, you can scale it up or down. And a tool that's super helpful is the double number line. Or as you see here, a bar model or tape diagram. They're all very similar in how you set them up. So this is the learning goal from day one. I'm wondering, Jon, how do we then ... So after day one, we give them some consolidation prompts. We consolidate the learning. We make sure students understand that yeah, this is a really cool thing. Make sure they see the behavior. We give them a couple consolidation prompts. But just like in the cutoff practice at baseball, we don't go, "Okay, now just be ready for it at game time." It's like, we need to make sure that, "Okay, are you really comfortable?" You know when flowers and boxes are here, you might recognize to use this, but where do we go next to help them see it in other places in their life?
Jon Orr: Yeah, it doesn't just end there after those couple consolidation prompts, which is that misconception I think a lot of teachers have when they stumble upon the resources on our tasks page. But also when you're seeing this done in other classrooms or on social media, you're seeing these types of lessons for thinking of students and then going, "Okay, well, what's next? How do I embed that next piece?" And for most people, the next piece is, let me just give some practice questions on these strategies. But what we've structured and what we recommend is what we have listed in our day two section on our tasks, which doesn't necessarily mean it's the second day even though it says day two. We've structured most of them to be about five days, but it depends on the timing of your block. Some people have a 50 minute block. Some people have an hour block. Some people have an hour and 15 minutes. Some people have 90 minutes. So it depends on what your block time is.
We've structured these to be more in the shorter timeframe for each of the days. But for me with an hour and 15 minutes, I might do day one and day two all in the same day, the same lesson, the same period of time with my students. Because day one, I'm going to emerge the ideas, the strategies that we just talked about with the flowers and the pots on the double number line and scaling along that double number line. But then I might move into the next piece, which isn't just jumping right into a purposeful practice. What we are going to do is we're going to elicit this idea of a math talk and then a purposeful practice section.
Posing purposeful questions for our students, but also having them engage in mathematical discourse is very important for us in our math class. So we might have our students watch a visual math prompt, or we might give them a number talk at the board. It might be just a picture. It might be even just a statement. And we're asking kids to turn and talk to their neighbors and then share some strategies about how to answer a particular problem. Kyle has up on the screen ... There's a number talk question. These prompts also are not the same type of prompt we had on the previous part of the lesson. It's not like we're going to go right into it. These are designed to be a little quicker, a little bit easier to think about and use the strategy. So I think it was we had eight apples and four baskets, and it's like how many apples are per basket?
But what we're trying to do is elicit, how do we use the model and the strategy to answer this with our class? And the other thing to keep in mind is that we have a series of these math talks one after the other that we can do in order. And a lot of times we craft that order to bring out those curve balls, to use your baseball reference, Kyle.
Kyle Pearce: Curve ball. I like it.
Jon Orr: Like the cutoff. How do I help kids practice the cutoff? You said, sometimes we don't hit the ball to them like we did in the first part. We hit it over there or we hit it short or it's a ground ball. We tried different things. Or all of a sudden the player is not on second base. Who is going to step in next? And that's what the math talks are designed to do. They're designed to switch this up a little bit and then switch it up a little bit more and then switch it up a little bit more so that by the end of a math talk series, you've tackled different aspects, but you've had kids thinking, talking and using the models and strategies instead of just sending them to a worksheet at that point. So they're carefully designed that way. And if you're going to make your own, I think one way other people have done this ... When you hear Peter Liljedahl's work, he calls that thing slim, Kyle. I just-
Kyle Pearce: Slim-
Jon Orr: Slicing. He calls it thin slicing. It's a math talk in a way where he has kids work at the boards and it's a small piece of a problem and then it changes slightly. And then by the end you've practiced lots of different aspects of the skill you're trying to emerge. Our math talks are designed similarly for that purpose in using it in that way. So that's what we would do next as a math talk. Kyle, what are some tips about math talks that I've left out here for our listeners?
Kyle Pearce: Yeah. Absolutely. And probably a good time for us to highlight that. Actually we did a full episode, episode 156, on why use math talks and how to ensure they're effective. So that's a great one if let's say this idea is something new to you. Sure you've heard of them. Maybe there's some teachers in your building using them in some way, shape or form. In that episode, we unpack different ways in which you can go about it. So for example, some people do number talks where it's just working on number fluency the whole time and it may, or in a lot of cases, it doesn't relate to what you're doing that day or in that unit. We're using a math talk throughout our units as almost a segue or to take where we were, practice that but then like you were saying hit the ball a little deeper, a little farther to the right, maybe a little shallow.
We want to give students an opportunity to build this fluency and flexibility while introducing again, a little bit more conceptualizing as we go. The thin slicing idea that Peter talks about is very similar to how Kathy Foznot would call it a string of related problems. So she calls it number strings. And she uses them to connect in her units. She's got some great ideas out there in units that are worth checking out as well. So up on the screen for those who are on YouTube right now, you'll see the string that we have. And you'll notice we did put some visuals there. But keep in mind every number talk that we do or math talk that we do, you can do purely using just verbalizing the scenario. So to be honest, the visuals that are here I find are more helpful for the teacher to learn how to facilitate the math talk.
All right. So a lot of people think Kyle and Jon always have videos and visuals and so forth. Most of the time I'm going to argue that our visuals ... We rarely show the visuals to the kids, unless it's just with the prompt. We use the visuals for the prompts, but the consolidation where some of you just saw this a few minutes ago, I'll show a couple screenshots, where you see the double number line of the eight apples and the four baskets and then we scale down to the two to one ratio, which is two apples per basket. You can see the rate being revealed here. This idea, or this visual, I would want to do this with the students. I would want to actually draw this number line using student thinking, because if I'm just relying on the video to press play and let them watch it happen, then they don't see necessarily their thinking emerging here.
They're like, "This video was already created before we said anything so I don't see my own thinking here." So I would much rather do it on my document camera or on the board, or however you choose. These visuals are more for you to get yourself set up. So with that, why I think that's important is because you'll see the string that we gave is eight apples to four baskets, then 14 to two. 27 to three. 32 to eight. Then I'll talk about the last one in particular in a moment. But just to address the first four in this string. If you do not need the visual that we've created, this means that you are free to modify the ratios to what you believe your baseball team needs in front of you. So if you think eight to four, 14 to two, 27 to three is too easy for your group ... Maybe they know all their math facts and you want to do something more challenging, rock and roll.
As long as it doesn't distract from the big idea that scaling can be helpful here and the double number line is a great tool to not only use it for thinking, to reveal the idea, but to also represent their thinking. So if you've got some students in your class that are like, oh, they're going to know the answer right away, my question to you is can they model it on a double number line? And if the answer is no, then maybe these are exactly where they need to be for this particular idea. Now, the last problem in the string, which is this ... Remember we talked about iterating. Coming back and of almost extending a little bit here. Conceptualizing something slightly new, but still related. We give six to four. So six apples to four baskets.
And the reality is if you have students that haven't really thought conceptually about mathematics ... So this would be like in my first 10 years of teaching, when I asked high school students to do something like six divided by four, most were like, "I don't know what that is." They're like, "I don't know, because it's going to be a decimal number." In their minds are like, "If I punch it in the calculator, a decimal's going to come out." They weren't thinking fractionally because they didn't have the tools, the strategies, the models. But when you think about this, six to four, if I'm using scaling ... So for eight to four, we went four to two, two to one. Awesome. 14 to two, seven to one. Awesome. 27 to three, that one's a little trickier because you're going I can't just halve. I'm actually probably going to think of it more as a thirding. A thirding strategy.
27 to three is the same as oh, nine to one. Okay, great. 32 to eight, same idea. Six to four, I could go three to two. And if I try to halve again, I get three halves to one. Three halves to one. So my rate is three halves of an apple to one basket or three halves per basket. This works even when the result is a fraction. That is pretty awesome. So we're doing partitive division. We're doing eight divided by four, 14 divided by two, 27 divided by three. So think of how powerful that is if it's two large, not so fun numbers, if I know that I can scale them to make them more friendly, wow, I can do so much with that along a double number line even if it's just to get an approximation. If I get this idea and I go, "Huh. I can scale these using facts that I know and using a tool that I can rely on. I can do a lot with ratios without having to rely on a calculator and without having to rely on say a mindless procedure like cross multiplying or something along those lines.
Jon Orr: Yeah. That's a great example and great tips there on the math talk, which is one of the next steps we do and oftentimes the actual next step after we've done our problem based lesson. And then from there, our next step after that in our lessons is our purposeful practice piece. And this is the more individual practice, but it also could be, say, group practice at the boards. You can choose that part yourself. While some days might lend better to working together on purposeful practices at your thinking classroom type setup at the boards, but also it could be individual practice. I know creating a mix of that is important to help kids keep some of the format changing a little bit, but also giving kids different aspects of what caters to them. So individual practice time, group practice time. Could be some on one day, some on the other day, but I think purposeful practice is important.
And that's the part that we want to bring back here is that we definitely need to practice the cutoff. Practice hitting the cutoff individually and in a group. So we just stay continually linked our conceptual understanding to some practice with our math talk and now we're going to move into, let's just practice some of these strategies and using the models with each other, but also individually. So what does that look like? What does that sound like from a purposeful practice standpoint? And I think this is the part where most times it looks like let's pass some worksheet or pick some problems from the textbook out. That's happening in our classrooms as well. But this is the part I was talking about at the beginning of this podcast about the intentionality.
So for me, when I'm choosing problems, it's not just let me just grab the worksheet and toss it at them. There's a lot more intentionality on which problems I'm going to choose. So my goal in my class is to build fluency around the big idea and the model that we've emerged. So in terms of the planting flowers and using the scaling along the double number line, I'm going to think about what problems lend to that? Can I create another progression or can I look at some of the problems that I can see and create another progression that allows my students to become fluent using these ideas in their practice? And I think that's important. We've been reading the book from Jennifer Bay-Williams, which we've just had on the podcast on fluency and Figuring Out Fluency, her book series. And part of that book has a chapter about practice and worksheets. And she often says, "It's not about giving them 32 problems, but if you did give them 32 problems, maybe the question isn't do all 32. The question is which of these problems makes it easy to use the scaling strategy for? Which of these problems makes it hard to use that strategy for?" Get them thinking about the strategy and the model as the vehicle you're using to do the practice because that's that intentionality piece we still have to continue with when we get into the purposeful practice.
We want our kids consistently making that loop. Conceptual back to practice. Conceptual back to practice. And I think just handing them that worksheet isn't good enough for the practice. We have to actually pick and choose which problems. So oftentimes we're choosing less problems. In our problem based unit if you go and look, we created purposeful practice questions that follow the math talk already. So it's embedded in our units as well. Every one of our units has that piece that you can print out and download. But we've carefully crafted those purposeful practice questions to continually eliciting the big ideas of that particular lesson.
Kyle Pearce: I love it. And Jon, the things, the examples you just gave, I think are so key because you'll notice up on the screen for our YouTube watchers right now, you'll see some of the examples of purposeful practice that we've given. By no means are we saying we give four problems or five or six or whatever. We're giving you examples of what might be helpful and you have to decide what makes sense. So going back to my baseball practice with the cutoffs. I had planned to spend a certain amount of time practicing cutoffs, but there was a point where I could see that we had done all we could do that day on cutoffs. You could see it in those players' faces. It was like, okay, we need to move on to something else. For you, it might be after a couple of these. Maybe you just want to hand pick two or three of these, or maybe you've got a group that's like, "Hey, I could do five." Or maybe they need a few more. That are number five here where we're asking them to think and conceptualize.
So you'll notice that there's a variation between these skill based, giving them an opportunity to practice the skill, but then we're also asking them to do some of the thinking. I love the question you were saying. Which problems does scaling work well for? And another great problem that's an easy problem that you can apply to so many different concepts is giving them and say, "I'd like you to make up a problem where this strategy would be helpful or really efficient. And I want you to make up a problem where it's not efficient." Think of the work that they'll be doing in order to craft those two things. So not only are they thinking about it, but they're also getting some of that procedural fluency as well, because they're going to have to do a couple problems. They're going to have to test it out. They're not just going to randomly pick a couple out of a hat. Some students will, and you're going to have to obviously have that discussion with them about how you want them to be spending a little bit more time and care in some of this work that they're doing.
So trying to find a way to help them with practice without it being boring, without it being overwhelming, without it feeling like they just are getting the same stuff that every single class has had in years prior. That was the old me. I had my homework picked out and that's exactly what I gave every single group every single year, regardless of where they were in the learning process. Make sure that you're doing it with intentionality. What's the purpose of this work? Is this helpful or hurtful for the group that you're working with right now? And where are we heading to next? So those are the big ideas here.
We'll talk about our big takeaway in just a second. But I do want to mention too, as you can see on the screen, we've only really addressed day one and two of this five day unit. So for those who have never used one of our units, it's like day one and two offer this conceptual to procedural and then extending idea into day three, where day three actually allows us to continue building this idea. The prompt on day three actually looks and introduces the idea of comparing ratios. So we're talking about actual multiplicative comparison ratios. So we flip the script on the students a little bit. They're like, "Wow. After day one and two ..." And we love doing this by the way. Math is so great to surprise kids because once they're like, "I get ratios," they're like, "Wow." We've only looked at composed units ratios day one and two. And then all of a sudden we give them this one where we're comparing the height of different sunflower plants. So you're looking at this and you see the Russian and the elf and you're like, "Wow. What do you notice? What do you wonder?" All of these things. And now the question is how many times taller is the Russian mammoth than the ... Is it the Pacino or the Pacino? I'm not sure how to pronounce that one. But we're going to compare these two sunflowers.
And what they're going to find is, wait a second. We don't actually have a composed unit ratio anymore. Now what we're going to be doing is we're actually going to be flipping the script from partitive division, because when we're doing multiplicative comparison, you're actually using quotative division. How many times does that go into that? And now they're like, "Whoa." Their minds get blown. It's like everything I thought that was true about ratios just got thrown out the window. And then we get to emerge the idea that, wow, there's actually two types of ratios or two ways to think about ratios.
And when you think about this type of ratio, the type of division changes. So this scaling and tandem idea isn't as helpful because now we're looking at a direct comparison between two completely different sunflowers and it's the same unit. Oh my gosh. It's so crazy. There's so much awesomeness here. And then of course, the next day we would have a math talk and we'd do more purposeful practice and then we would compare and contrast, what have we learned this unit? What can we say about ratios? When I have this ratio with this stuff going on, I can do these things and this model's really helpful. When I have this scenario going on, it's still a ratio, it's just a different way of looking at ratios and it's going to change some of the behaviors and this model and these strategies can be helpful over here.
That for us is what math is all about. It's the intentionality. Introducing these ideas, but then not just leaving them hanging. We've got to give them an opportunity to practice and work through these ideas so that they can develop a true understanding and true flexibility with these ideas. And I think this particular unit that we've highlighted here today, this planting flowers unit, Jon, is one of the most awesome units ever. And if you are doing ratios and rates and any of this is confusing you ... You're like, "Wow. Composed unit, multiplicative comparison, what's the difference?" Dive into this unit, my friend. You are going to learn about things that have always been there that you never noticed, and you'll get to share these new ideas with your students so that they can feel confident and ready to go in their math class.
Jon Orr: I think you've just done a great job as our big takeaway here, Kyle, and I think one more thing to add about, say, looking at this particular unit. If you're not teaching ratios coming up, or that's not even in your course, think of even diving into that unit and seeing how it's pieced together to give you a sense of how you can design your lesson to be a problem based lesson, but then what comes next. Have a look at day two and day four to see what the math talks look like and how the string has been pieced together and then the purposeful practice questions are related to that. So being a big takeaway here is that we wanted to revisit this big question that we've had about what do we do next after a problem based lesson and then we're talking about making sure we bring that intentionality along. And we have to think outside of that very specific learning goal to think about what are the big ideas I want to bring about with my problem based lesson? Oftentimes it's a strategy and a model that should help kids use those. That's how we're going to become more fluent is giving them strategies and models that they can use. Not only in just that lesson, but in other lessons. So we want to do that.
That's usually our big idea, our main intention of a particular problem based lesson, but then the purposeful practice and the math talk also have to strengthen and get towards more fluency with those strategies and models. We have to keep that going. That doesn't just drop off. We want to be very particular about what we're doing with our talks and our purposeful practice. So that's what we've wanted to share with you here is that, hey, we do have to make sure we're bringing purposeful practice into these lessons. We're not forgetting about it. And oftentimes when we see some lessons out there that are problem based, we think, oh, we're just always doing that. And when do we build that in? Hey, we do have to specifically build time in for that just like you're building time to hit the cutoff and practice in your baseball practices.
Kyle Pearce: I love it. I love it. Thanks for that summary there, Jon. Wow. I'm feeling energized after this discussion. I know that as this episode goes live, lots of new school years are underway. If you're listening to this well into the future, maybe that's not the case for you, but we're excited. We're excited for all of you who are listening to this as this goes live, and we wish you all the best in this new school year. Remember, my friends, we have over 50 problem based lessons or units, I should say. Not lessons. They have problem based units, but they also have the math talks, the purposeful practice, all built in. Go check them out over on makemathmoments.com/tasks. We should really change that link, right Jon?
Jon Orr: Right.
Kyle Pearce: Because it's not just tasks. It's the full gamut. And all of the teacher guides there to help guide you as you deepen your own understanding to help more students feel confident and capable as mathematicians in your classroom.
So right here, my friends, what are you going to jot down and reflect on? Because remember, we don't want all of this learning to wash away footprints in the sand. Are you going to pause the podcast as you're walking and talk into your voice memo recorder so that you can go back to it later or put it into your notes using Siri or Alexa or whoever you're talking to do all the writing for you? Or are you like me and you like to actually jot it down point form on a piece of paper? However you choose to reflect, make sure that you do spend the time so that your brain knows, hey, there was some important information here that I want to make sure I hang onto today.
Jon Orr: And don't forget, you are not alone in this journey. We do have communities. There's social media. There's lots of folks out there who are doing the same type of learning that you are doing right now. You could join up with us on our Facebook page or our Facebook group, Math Moment Makers K to 12. Lots of great discussions about different aspects of math lessons happening in there. There's lots of people saying, "I'm teaching ratios. Which lessons should I use?" So jump in there. Feel free to post questions and wonders in there. Also you can tag us or reach out to us on all other social media at Make Math Moments on Twitter or Instagram or all of those other things. So make sure that you have someone that you are reaching out to if you need that support. We're there for your support as well.
Kyle Pearce: My friends, it has been awesome. Last few episodes we've been asking friends to just take a moment, pause, hit that ratings button on whatever podcast platform you're on. We see them all coming in and it is so fantastic to see. Even if it's a one or two liner, that just gives us a little bit of energy to keep ongoing in this journey. And not only does it help give us feedback to let us know what you're thinking, what you like and what you want more of, but it also tells all of these crazy search engines out there to share this with more educators in the world so that we can build this Math Moment Maker community. So thank you to all of you. Take that moment now, pause, hit that ratings and maybe leave us a review and let us know what you're thinking there.
And also remember, we are always looking for more friends to join us on our mentoring moments episodes. We get nothing but a fantastic jolt of energy when we chat with friends like you who bring common struggles to the forefront. I know you have to be a little bit vulnerable, but remember you're not just helping yourself. You're not being selfish. You're actually helping so many others because everyone else is struggling with many of these same problems. So go on over to makemathmoments.com/mentor. You'll just literally need to take two minutes to tell us your name, your email, and a one liner of what's that pebble in your shoe and we will reach out to you in the near future to set up a date and time. So once again, that's makemathmoments.com/mentor, and we hope to chat with you real soon.
Jon Orr: Show notes and links to resources and complete transcripts can be found over at our show notes page, makemathmoments.com/episode196. Again, that's makemathmoments.com/episode196
Kyle Pearce: Well, my Math Moment Maker friends, you know what that means. Until next time, I'm Kyle Pearce.
Jon Orr: And I'm Jon Orr.
Kyle Pearce: Hi fives for us.
Jon Orr: And a high five for you.
Sign up to receive email updates
Enter your name and email address below and we'll send you periodic updates about the podcast.
DOWNLOAD THE MAKE MATH MOMENTS FROM A DISTANCE CHEAT SHEETS
Download the Cheat Sheets in PDF form so you can effectively run problem based lessons from a distance!
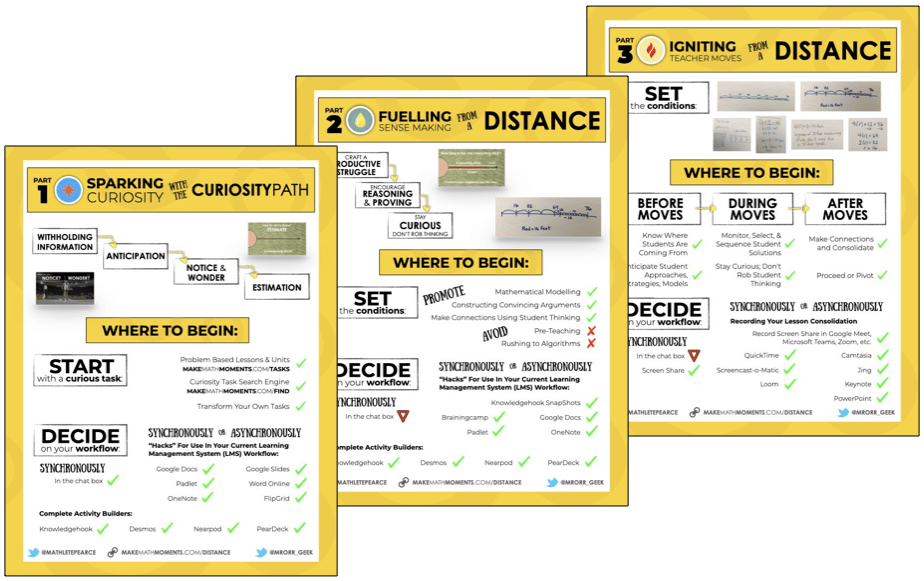
UP YOUR DISTANCE LEARNING GAME IN THE ACADEMY
There is a LOT to know, understand, and do to Make Math Moments From a Distance.
That’s why so many Math Moment Makers like YOU have joined the Academy for a month ON US!
You heard right: 30 days on us and you can cancel anytime. Dive into our distance learning course now…
Thanks For Listening
- Apply for a Math Mentoring Moment
- Leave a note in the comment section below.
- Share this show on Twitter, or Facebook.
To help out the show:
- Leave an honest review on iTunes. Your ratings and reviews really help and we read each one.
- Subscribe on iTunes, Google Play, and Spotify.
ONLINE WORKSHOP REGISTRATION
Pedagogically aligned for teachers of K through Grade 12 with content specific examples from Grades 3 through Grade 10.
In our self-paced, 12-week Online Workshop, you'll learn how to craft new and transform your current lessons to Spark Curiosity, Fuel Sense Making, and Ignite Your Teacher Moves to promote resilient problem solvers.


0 Comments