Episode 197: Figuring Out Fluency – An Interview with Jennifer Bay-Williams
LISTEN NOW…
WATCH NOW…
In this episode we speak with professor, author, speaker Jennifer Bay-Williams. Dr. Bay-Williams is an internationally respected mathematics educator, a prolific author and popular speaker on topics related to effective mathematics teaching. Her most recent work has focused on fluency in mathematics, communicating that it is more than learning facts and algorithms, but is about being able to reason and choose appropriate strategies.
In our episode we chat about how we can help students (and parents) build flexibility and efficiency around basic math facts. Stick around until the end and you’ll hear great tips on how you can easily build fluency into your classroom.
You’ll Learn
- How can we get students to basic math fact automaticity as quickly as possible?
- How can I put students in a decision making role?
- How we can get started with teaching students flexibility with basic facts.
- How we can help parents realize the difference between fluency and memorization.

FULL TRANSCRIPT
Jennifer Bay Williams: When students memorize, it is stress-inducing because they have no backup if they forget. You put them in a stressful condition and they forget. You hear of people in crisis that forget their phone numbers and things like that. That's what we've done. When we pair memorizing and time tests, we're pairing two of the worst things together. But they can get to automaticity through the strategy instruction. Then what comes along with it is their number sense. And it's their number sense that leads to that positive math identity. So, I'll stop there. There's a lot more to the story of how to do that.
Kyle Pearce: In this episode, we speak with professor, author, speaker, Jennifer Bay Williams. Dr. Bay Williams is an internationally respected mathematics educator, a prolific author, and popular speaker on topics related to effective mathematics teaching and instruction. Her most recent work has focused on fluency in mathematics, communicating that it is more than learning facts and algorithms, but is all about being able to reason and choose appropriate strategies.
Jon Orr: In our episode, we chat with Jennifer about how we can help students and parents build flexibility and efficiency around basic math facts. Stick around until the end and you'll hear great tips on how you can easily build fluency into your classroom.
Kyle Pearce: Let's do it. Welcome to the Making Math Moments That Matter podcast. I'm Kyle Pearce.
Jon Orr: And I'm Jon Orr. We are from makingmathmoments.com. And together-
Kyle Pearce: With you, the community of math moment makers worldwide, we want to build and deliver math lessons that spark curiosity-
Jon Orr: Fuel sense-making.
Kyle Pearce: And ignite your amazing teacher moves. My friends, math moment makers, we have the privilege and honor of speaking with Jennifer Bay Williams here today, who as we mentioned has done so much in the math space. Where I was first exposed to Jennifer's work is through the Teaching Developmentally book for elementary and middle school mathematics. That is a Jon Van de Wallle and team book. And it is fantastic. And actually, she talks about just briefly about how the 11th edition just got released.
I actually leveraged that resource as I wrote the proportional reasoning course there, The Concept Holding Your Students Back, that was my main guide as I was learning and understanding ratios, rates, and proportional reasoning in ways that I had never really understood them before.
And now, we're deep into their Fact Fluency series, which we're going to talk all about here on the episode. Jon, it was an awesome conversation. What was your big takeaway or something interesting that resonated with you before we dig in?
Jon Orr: Yeah. You said the work that she's been doing is heavily influenced what we've been doing. I'm reminded of her Figuring Out Fluency book series that you also referenced, that we ran a webinar not too long ago. We referenced her work specifically about worksheets and how you can build fluency and how we can use worksheets in a very specific and particular way to do that. She's got some great ideas on how to do that. We're going to talk about them here in this episode as well. So, let's get into it. And here's the conversation with Jennifer.
Kyle Pearce: Hey, Hey there, Jenny, thank you for joining us here on the Making Math Moments That Matter podcast. How are things going in your world? Sounds like things are pretty busy as usual.
Jennifer Bay Williams: Yeah. Things are busy, but they're going great. I'm thrilled to say that the Fluency series is done. It's out. So, that means that I'm not juggling the writing and speaking as much. So, that's been great. And it's the beginning of a semester at the university campus that I work at. So, things are buzzing around campus as well.
Jon Orr: Amazing. Yeah, we are definitely going to be diving into that series. I know that Kyle and I read, I think the high school version and the algebra concepts with proportional reasoning. So, I'm excited to chat with you about all of that. Jenny, tell us a little bit about yourself and our listeners probably will want to know that where are you coming from right now. And also, give us a little backstory into your journey into education, a lot of our listeners want to know about our guests, and how do you get from where you were starting your career into where you are now?
Jennifer Bay Williams: All right, so I'll try to keep this short. But first of all, I went through high school thinking I could never be a teacher. They worked too hard. They get up too early. And I went off to college, not knowing what I wanted to do. And then, I signed up to volunteer at an elementary school. And I worked with a boy who was struggling with his basic facts, which is poignant for me. Today my life is, as you know, because I'm really passionate about basic fact fluency. That experience was so profound that I enrolled in my first education class. So, that was just a one day in the life. And luckily, I signed up to volunteer that day.
And then, fast forward to teaching, and I'm teaching in my class. I'm a middle school teacher. I'm noticing that students are doing goofy things like using a standard algorithm when they don't need one. And they don't really like math. What? I always liked math. I'm teaching kids that don't like it and it doesn't make sense to them. And so, I took graduate classes. I started thinking harder about this and other ways to teach. The standards were just coming out in the US, the original standards, by the way, because I'm old.
And so, I started thinking about helping students make sense of what they were learning. And then, I started thinking I need to work beyond my classroom. I got to work at the school level and to do that, I need to learn more. Then I got an interest in writing and I wrote my first book and that's another way to just advocate for effective math teaching. And fast forward 20 years, and here I am.
Kyle Pearce: That is fantastic. What a story. And it's great. We always love to start at the beginning because there are so many educators out there and it's not just in education, it's in any space where, when people are successful and confident and doing great work, oftentimes, we have this idea in our mind like they always were there. They always had it together. They always knew what to do. And it was almost like it was innate. And just like in math where we're not math people or not math people, it's like those experiences, the learning along the way. And it sounds like that lifelong learner in you has allowed you to start from never thinking you could be a teacher to doing what you're doing now.
And I'm picturing how you were envisioning the world as a teacher when you were in high school and you weren't even considering the fact of writing, speaking, consulting, chatting on podcasts like we are here. And look at you now. So, just showing how things change, things evolve over time. I think it's always great to highlight those messages.
I want to take a moment and go back again to ask you the question we ask everyone on the podcast. So, everyone's always waiting for it. And it is, what would you say your math moment as a learner would be? We don't limit it from K through 12. It could be later in life as well. But as you as a math learner, what's that moment that pops into your mind when you think math class?
Jon Orr: Do you want us to give you a small example?
Jennifer Bay Williams: Give me an example.
Jon Orr: Sure. So, for example, some people say something that was a negative experience that just stuck with them like that's what my math moment is, similar to Kyle's. But some people say a positive math moment. So, for example, mine is I have this very vivid memory. When I think of math class, I think of my... it was grade four and my teacher used to give me multiplication questions. You're practicing, I think was one digit by two digit multiplication, or it might have even been two digit by two digit multiplication.
It was just like one after the other. And I was the student that would be like, "Give me the rules. I will mimic those. And I will do it a million times just because I know the rules."
Kyle Pearce: And feel good about it.
Jon Orr: And so, I would get some, and then the teacher said, "You can do these extra ones if you like." And so, I remember going home and just pounding out pages of these one by two digit numbers and coming back. And then, all of a sudden I have this big sticker on my book. And it's like this not normal sticker. It's one of those puffy hologram stickers. And it's like just memory stuck out. Why that memory stuck out is because actually I found this not too long ago. My mom had saved some of my grade four work and I had this test that had eight out of 25 on it as a mark. And I remember having that sticker.
But then, all of a sudden, this mark is saying, you know what, I could do these things. But then, actually, when I had to try different strategies, I was terrible at it. And it just stuck out for me to say, "I was this master multiplier in one way," but actually didn't understand what I was doing in another way when I reflect back on it now. And that moment have always stuck with me.
So, we're going to turn it back to you. What would be a moment that sticks with you as again... mine was a negative thing, but it can be positive or negative.
Jennifer Bay Williams: I have these moments in time and I got to say some of them are more negative than positive, which is interesting because I've always loved math.
Jon Orr: Most of them are.
Jennifer Bay Williams: Yeah.
Kyle Pearce: Sadly.
Jennifer Bay Williams: That's sad. It is a big message that we'll come back to when we talk about fluency that those kids carry so many negative memories from the fluency work. So, I'll pull from my fluency life. I remember the planetary system. And if you mastered your threes, then your little person got out to earth. Memorizing your facts, you move out, and whoever got to Pluto first, because Pluto was a planet at the time was the first one to master their multiplication facts. Well, I got sick. I think I might've been on Saturn. I got sick and I was so sure when I came back to school-
Kyle Pearce: Was it something to do with the air like on Saturn?
Jennifer Bay Williams: I was pretty happy there, but I really wanted to be the first one to Pluto So, I got sick and I just sat at home worrying about whether somebody was going to get to Pluto. I was so sick. How tragic is that? And now, I'm so opposed to those words that compare students' memories. And then, another thing I would share about myself if I get a second one.
Jon Orr: Sure.
Kyle Pearce: For sure.
Jennifer Bay Williams: Is that fast-forward to high school. And I really realized about myself that I loved hard problems where I hadn't been told how to figure them out. And while I'm very gregarious and social in my world outside of math, I don't really want to talk to somebody when I'm doing a math problem. So, I had a real identity awareness thing that when I'm doing these tough problems, I really just want to think. I don't want to be with a partner. I don't want to do anything. Anyways. I've learned that I like to talk about a problem after I figured it out and everyone's different in that way.
Some people like to vet ideas collectively, but I would love doing those tough problems. And when I would come to school the next day to share homework. Then, people would be like, "Jenny, did you figure out number, whatever, the hard one?" That put big pressure on me to figure it out, but I figured it out. So, I loved that feeling.
Kyle Pearce: Well, I loved too just hearing in your message, especially the second one here, the message around identity and that we have to be aware of the learners in our room. And while Jon and I often are promoting collaboration, there's the caveat that we have to also understand that for some students, that might be very uncomfortable and we have to also understand that might not be how they choose to think and learn. So, we have to be very flexible and supportive with students in our classrooms that it's not a one size fits all.
I think in education and just human nature is we're all-or-nothing type creatures. In between is really difficult for us. And I think that connects really to our conversation around fact fluency as well, because I think we have this on-off idea. It's like you know your facts or you don't or do it in a really boring, mundane memorization way, or you don't know them at all and there's no in-between. There's no other opportunities. And I'm sure your messaging today is going to help to highlight that that's actually not the case.
So, I'm wondering, based on those experiences and where you are now, you had referenced this experience in your own teaching journey where students were either blindly following steps. We call it rushing to algorithms, where it's like, "Hey, I see a multiplication problem. Mr. Orr told me that this is what you do when there is multiplication with three digit by two digit," or whatever it might be, instead of really zooming out and reasoning through problems.
I'm wondering for you, you had just said in your secondary classroom, you started to realize, or as a student, you started to realize that you enjoyed more challenging problems. I'm wondering, did that help you maybe get to this place in your journey earlier as a teacher? Because I know for Jon and I, our experiences, I'll be honest and say, I didn't like the hard problems because it exposed me as actually who I really was, which was a memorizer. It exposed me as actually not being maybe as mathematically proficient as maybe I thought I was based on the grades I was getting.
Do you think that experience had impacted the speed at which you landed in this place where you were like, "Whoa, whoa, whoa. We need to do something here with fact fluency. We need to help students build strategies and actually reason through problems." I'm always curious about how long that took you. Because it took me, I feel like a very long time before I started to realize this isn't really working for all of my students.
Jennifer Bay Williams: I had a rough first year of teaching and like I said, my students didn't like the class and I totally took it to heart that I wasn't teaching in a way that was reaching them. And so, what I noticed is they wouldn't do the story problems that were at the end of a page. And I thought, "Haven't they figured out that the story problems at the end of the page, use the same math? They were just practicing. They don't even need to read the story. They can just lift the numbers out." And so, then, of course, I had students who didn't figure that out. They knew they could just lift the numbers out and do whatever they'd just done 25 times in their practice set.
So, I'm in my second year of teaching and I did do all this professional development and I took graduate courses that focused on these brand new draft version of the standards about reasoning, problem-solving. And so, I came into my second year thinking, "I am not going to be that skilled teacher. That did not connect to my students, that didn't work." And I had a lot of the same students that next year and day one, we just started with stories. It could be from the end of the page of the problems in the book, but I would do it first.
Or I'd go find what they'd call enrichment and I'd pull that story in or I'd go look for other resources in the textbook series. I hadn't really yet discovered that there were idea books out there. So, I really had my textbook and not much else. And it was pre-internet. So, where do you get your ideas from? Either in your head or in your textbook. That was it. And I noticed this dramatic change in my students in September, where they were excited to be in a group. I'd put them in a group, I'd put them in group roles and they'd have a problem to solve. And it was phenomenal.
The very same students I'd had the year before, it wasn't like I got better students. They were just more engaged. I never had a behavior problem. I'd had so many behavior problems the year before. And in part, I had more of a presence in the classroom, but a lot of it was that I decided to use stories and problems and group work. So, I was there year one.
And so, then, part of me now is how can we still be teaching skills based? Haven't you noticed that it doesn't connect to kids and it doesn't get them where they need to be in terms of their lives?
Jon Orr: Exactly. Well, I find that, like you're in year one, you said you hear from your students that you're not helping them in a certain way. And I think teachers get stuck in this loop of hearing kids that you're trying to give them algorithms, give them procedures like you were in year one. We were up to year 10, and congrats for you for doing it in year two and making a change.
Kyle Pearce: You did it in 1/10th of the time which is I think is amazing.
Jon Orr: We took a long time to all of a sudden change. But I think when I reflect now, it took 10 years of me hearing my students go, "I'm not very good at math. I'm having trouble with these algorithms," to me going, "Okay, let me speak louder. And let me speak slower to telling you this thing again." Because we're hearing, you're not helping me. So then, we're like, "Well, I want to help you the most. So, I got to actually tell you exactly how to do it." Because that's the way we get stuck in thinking how to help kids is tell them how to do things, instead of letting them experience, letting them learn through story, which I think took us so long to learn just like it took you quickly to learn about storytelling.
I think that fuels the work that we're doing now with Make Math Moments is teaching through problems, teaching through stories that we realize just like you did early, that kids actually connect to that better. And that's how we can get a window into helping them, which is really what we're trying to do. But we needed to realize we're helping them in a different way. I want to make sure that we get into the work that you've been doing for the last few years. And I want to start with fact fluency specifically.
Because I think it's a great place to start because I think there's a lot, especially being a middle school and high school teacher and thinking and hearing that so many teachers are saying, "Kids just don't know their facts." And here in Ontario, a few years ago, our curriculums changed and parents are saying, "Our kids need to know their basic facts." The government is saying, "Hey, we need to know our basic facts. We got to make sure that we're putting basic fact professional development into our professional development days." It became this big thing here specifically in Ontario to get back to the facts.
And what we've realized and knew, I guess in the last many years when this happened, that knowing facts from what parents are saying and what the government is saying is a lot different than what you're talking about and what we've come to realize about fact fluency. So, I'm wondering if you can highlight this miscommunication between what knowing your facts is and also what fluency is.
Because I think when we talk fact fluency, teachers go, "Oh, I know what that is. Let me just drill and kill because then they'll memorize it." And memorization is fact fluency where we know you don't believe exactly that. And so, I'm wondering if you want to fill in some gaps here from our listeners who are going like, "Wait a minute. I thought that's what it was too. What is it?"
Jennifer Bay Williams: Yeah, Jon, you've really captured the essence of the challenge around fact fluency. So, I'll jump in with some highlights. First of all, I think we all agree that we want this thing at the end, which I'm going to call automaticity. And that is that when a student sees nine plus six, they're like, "15," or they see seven times 3, "21." And that they can do it about that quickly without putting a lot of thought into it. How we get there is what's up for debate. And so, there's this pressure to get there as fast as possible. And that pressure to get there as fast as possible is leading to ineffective practices and they're ineffective in terms of learning of the math.
And then, they have this detrimental, emotional impact on students. So, for example, you mentioned memorizing. So, one way to learn seven times three is to memorize it. You look at it, you see it, you send it home, you keep having it flashed in front of you and you have it down. And then, you put it in a time situation, which I'll get to the assessment later. But then, you're just memorizing it. Another way to learn seven times three is to know your doubles, two sevens is 14, and that's one more seven as a bridge plan to where you become automatic.
And then, same thing with nine plus six is that if you can think about nine plus six as 10 plus six and one less, then not only do you get there very quickly, but you have a strategy that's going to serve you really well for 99 plus 6, 99 plus 26, and so forth. So, when students memorize, it is stress-inducing because they have no backup if they forget. You put them in a stressful condition and they forget. You hear of people in crisis that forget their phone numbers and things like that. That's what we've done. When we pair memorizing and time tests, we're pairing two of the worst things together.
But they can get to automaticity through the strategy instruction. Then what comes along with it is their number sense. And it's their number sense that leads to that positive math identity that we talked about earlier. So, I'll stop there. There's a lot more to the story of how to do that, but it's definitely strategies over memorizing and using that as a bridge to get to the automaticity.
Kyle Pearce: I love it. And honestly, what I'm hearing and we use this word a ton on the podcast and throughout any of the workshops that we're doing. Jon and I were in Texas last week and I use this word so many times and it sounds like you're asking students to be reasoning pretty much at all times. Eventually, they'll get to a place where they don't need to reason anymore. To me, that's that place where we get automaticity. You've been reasoning through these problems and thinking about, "What does it mean," whether it's addition and saying, "When I'm adding nine plus six, what does that really mean?"
And in my mind, you had given the example of 10 plus six minus one. You're reasoning through that. And eventually, that will turn into this automaticity where I don't need to think about it anymore. I just know it. And that knowing and having confidence is great. And the other piece I'm hearing from what you're sharing is when things do get tough, let's say you're in a stressful situation. Hopefully, not a time test. That's not the stressful situation we're talking about, but in life, there are going to be stressful situations when you can then pause and go, "Let me reason through this again."
Even though I feel like I know the answer to this problem usually, because I'm stressed, it's not coming to me. I can actually think about this problem. And then, these strategies and these models come to fruition. Now, there's no way we'll unpack it all in this episode, but just to get people maybe an appetite for digging into some of the Figuring Out Fluency series of books. And I know you have a general book, but then you also have different aspects. For example, one of the latest ones is Operations with Rational Numbers and Algebraic Equations.
May not sound super intriguing at first. But when teachers think about, "Wait a second, my students struggle with fractions. They struggle with algebra." It sounds like, wow, if I could do this in a way that's going to build automaticity so students can be reasoning through problems and then feel comfortable with these traditionally challenging subjects for students. I think it's definitely worth digging into.
So, there are components outlined in your books about building procedural fluency, which I think everyone thinks math facts and it's like procedure. But we work towards it. We work towards that automaticity. What are the components in general for people to be thinking about when they are trying to help maybe their children or their students develop fluency?
Jennifer Bay Williams: The simplest way that I would frame it is putting students in a decision-making role. So, they're deciding, how am I going to solve this? Instead of being told, "This is how you solve this. This is how you solve this. And this is how you do this." So, to me, me, it's about decision-making. And so, to bridge from the nine plus six example, another way we could solve nine plus six is we could move one over and have it be 10 plus five. So, that's a strategy, a make 10 strategy that graduates up to whole numbers, where if you have 29 plus 16, then you can move one over. And now you have 30 plus 15.
And then, you get to the book you're talking about with rational numbers and it's not make 10s anymore, but you could make a whole. So, if you have 2 3/4 plus 2 3/4, again, you're starting with decision-making. How do I want to solve this problem? Oh, I could move 1/4 over and make a whole. Now, I've got an easier problem I want to solve. And then, the same thing is true when you get up into the algebra examples. But you have this idea of teaching for fluency is teaching a strategy, helping students generalize that strategy so that they can use it. And then, you add another one to the repertoires.
And so, pretty soon, they have more than one option and they can start choosing strategies. So, that's the lifelong trajectory from kindergarten when their one option is counting to them adding onto their repertoire, a small set of strategies so that when they look at a problem, whether it's whole numbers, fractions, proportions, equations that they ask themselves, which of my things in my repertoire do I want to use first. That's teaching for fluency.
Jon Orr: And I think when you're saying these things, and I'm just reminded of the three big components that you've talked about in your books about procedural fluency. And when you say adopt the strategy or select a strategy, I'm just reminded of that flexibility piece. And I've been hooked on the flexibility piece for the last year or two on, and I teach high school classes, trying to help my students become more flexible with strategies. And I think that part is what many of us have missed along the way is how we teach kids to be flexible with strategies and also models to help them solve problems.
Because I think that's a part. We all talk about procedural fluency, but what does that really mean? It's like, oh, that means let's just get them to accuracy. Let's just get them to hump out a right answer instead of how do we get to that right answer. How can we teach kids to be more flexible? And you're suggesting we got to teach different strategies. I'm wondering if you have any tips and suggestions for teachers. I guess I know you have tips and suggestions for teachers.
That's what you've been writing about, for how a teacher can get started with just thinking about the mindset in your classroom with teaching flexibility to kids. I'm just imagining a teacher, let's say seventh grade teachers going in and go, "I want to focus on teaching my kids strategies and flexibility this year. I've been in a place where I mostly did direct instruction and taught procedures straight up the way that I was taught, the way I taught for a long time. How do I go about making that shift so it's manageable? What would you say to a teacher like that?
Jennifer Bay Williams: So, it starts with access. Do they actually know how to use a strategy? So, that can be very intentional like when they look at 2 3/4 plus 2 3/4 for you to help them see options. With proportions, there's not just the cross-product approach. Oftentimes, there's a number of relationship where you can solve the problem without having to enact that longer procedure. With equations since you brought up high school, eliminate parenthesis is not always your first step. And so, we have to look at the things where we're saying to students, "The first thing you do is blank." So, remove that.
But we teach them the options. So, that's the beginning. And then, we have these regular opportunities to choose among strategies. And that can be done through routines to start class with, which can be part of the lesson or it can be separate. So, one of the ones that I really like that's in the books is strategize first steps. And I like it for high school. I like it for all grades. But the advantage is if you're only thinking about your first step, then it's a much quicker routine than if you have to solve the whole problem.
So, you're just thinking about what would you do first on this problem? And so, you put problem number one up, and it's just a form of a number talk. And students share what they might do first, because that's brainstorming. That's giving them time at the front end to think, what are my options here? How could I solve this? And they see you create a menu from that first problem, then you put up another problem. And so, they can either pick from the menu that's up there, how they would solve the second problem or they can add to the menu.
You put up a third problem and a fourth problem. Well, strategically, you've come up with problems that fit different strategies. So, one might land to, if it's computation you're working on, for addition, one of them might be making 10. One of them might land to compensation. One of them might land to partial sums. And one of them might got nothing. I'm going to use my standard algorithm. But that menu goes up and they see that. Well, then that sets up if they're going to be working on a practice set where the purpose of the practice set is choosing your best option for the numbers in the problem.
So that instead of telling the students, solve using blank method, you're saying, solve using an efficient method. And that's those components you're talking about, Jon, when you said the flexibility, the efficiency, and accuracy, because they're a package deal. When you're choosing an efficient method, you're more likely to be accurate and the flexibility comes in making those choices.
Kyle Pearce: I love it. Another word coming to mind for me is the behaviors, understanding the behaviors of how the operators are working and then students being given the opportunity to essentially strategize based on what they're bringing to the table. And a question Jon and I receive a lot is how do you assess? And I think when people say assess, I think sometimes they confuse it with evaluate. People are thinking, "How do I evaluate fact fluency?" And we push it back to this idea of assess because no, we want to help students build their repertoire, but we don't want to necessarily evaluate.
So, an example I always use is I teach students how to double and half, and how that can be a really helpful strategy, but I very rarely use it myself. I'm like more of when I'm multiplying, I'm a distributed property, partial product guy. And that's what I tend to lean on. So, this idea of efficiency, I think, you're leaving it open for interpretation for students, right? Because I think what's efficient for Jon or what's efficient for Jennifer or what's efficient for me might be different depending on where we are and how we're reasoning through a problem. So, I'm loving these ideas here.
I'm wondering if you could help an educator make one small change. So, we're recording this. It is summertime here, but some US schools are heading back now. And if a teacher is listening to this and they're saying, "I want to make one small change, that's not going to throw out the baby with the bath water or anything else." Maybe there's other places or other things they want to change in their math program, but they want to add one little small change to help get them closer to working on fluency with their students.
What routine or change or idea might you suggest for them to squeeze in there that isn't going to leave them up for nights thinking about it as they try to restructure what they usually do in years past?
Jennifer Bay Williams: The first thing that came to mind when you were asking that question is in your textbooks or your worksheets that oftentimes in the instructions says how to solve the problem. So, a simple thing you can do is just audit your instructions. And when it says solve using blank, then just draw a little line through it. I have stayed up nights thinking about that, just draw a line through it or get your whiteout out, and then just replace it with something that's more of a fluency instruction.
So, in elementary school, there's a lot of instructions that say, solve using the standard algorithm. You could not cross that out. You could say solve using standard algorithm when it's needed, otherwise use a strategy of your choice. But alter the instructions so that you're offered an invitation to choose an efficient method.
Jon Orr: Yeah, I like that, specifically as a great example. I'm reflecting right now on your chapter of your book about practice work, homework, or not homework, it was worksheets. It was thinking about how do we build a good worksheet. Kyle and I actually just a couple of months ago did a webinar on how do you make a great worksheet and how do you use worksheets. And we actually referenced your work in that webinar, specifically when you discussed about building fluency or automaticity isn't a full worksheet of 20-plus problems.
I liked how you described that. Hey, give practice problems, where you are saying, which of these problems would be great to use this strategy for and which ones would you not use this strategy for? I thought that was such a great tweak you can do with, say, existing worksheets already because some of them, you know that these worksheets are created almost by computer and they're not meant to be used with, say, a particular strategy.
And I think that was also a great point from your work when you're thinking about the work that you're doing, like a particular skill. I want to highlight a strategy and which problems or what examples can I use to highlight the strategy and not specifically that particular outcome. Because if we teach strategies first and then the, say, specific outcomes follow, I thought that was a great point. So, I love that tip that you're giving teachers if they're trying things for the first time this school year.
One more thing before we go here, Jennifer, is I know that when I started the episode, we talked about how to change the mindset about this idea of understanding basic facts into what we're trying to talk about here. A lot of the push that we hear is from parents. And I think that's what happened here in Ontario when we had a government change and, "We're going back to facts." And everyone got their wires crossed about what that is.
We've chatted about that here. But I think there's still a lot of parents that are still saying, "But this is what basic facts means. And my kid needs to know their basic facts. Why aren't you sending home worksheet after worksheet?" What can you do-
Kyle Pearce: It worked for me.
Jon Orr: What can you help our teachers right now who are going into this school year going, "I want to do this too. I know I'm going to get pushback from parents." What do I say to them so that I can convince them that this is the right way for your kid to learn their basic facts?
Jennifer Bay Williams: So, one thing that I like to do with families, because they do another basic fact is to move up to two digit numbers and give a problem that could be solved lots of ways that does not land to the standard algorithm. So, for example, 49 plus 48, and then they're at an open house or something. So, they get to meet a parent next to them, share how they solved it. They get to talking, they feel joy and then you bring them back together and you're like, "This is how our math learning is going to be." You can debrief as much or as little as you want.
But when a parent says, "Well, I pretended both were 50 and then I fixed it." Say, "Okay, so with basic facts, when you add nine plus six, you could do 10 plus six, pretend it's a 10 and fix it." And another person might have moved one over. And so you can connect it back to the basic facts strategies, and they can see that there's value in learning the strategies because their child will develop stronger number sense, and they're going to be poisoned and ready to go beyond the basic facts.
So, again, you're talking to the parent about the benefits for their child rather than bash all the problems with basic facts, which I've spent decades doing literally. But for families, you want them to walk out feeling assured that their child's going to get a really solid beginning to math and really like math.
Jon Orr: I find that amazing too, because I think you're right. When you ask a parent to do that, they're actually going to use their mental math strategies that they've developed outside of school. Like their schooling. I feel like I've got those strategies now too. But when I reflect back to my schooling, I don't think I was ever shown what you're talking about. We would've done the algorithm and they're saying," Go into the algorithm," but that's not the way I do it actually in my head. So, I really like that example for the parents. Yeah.
Jennifer Bay Williams: We're taking it from the outside, we're bringing it inside to our math class. We're going to make sure the students have access to the best ways of reasoning.
Kyle Pearce: If you speak with carpenters or we'll call it the jack of all trades like my dad's a jack of all trades. I am not, but he is. And when he's working with a tape measure and he's using strategies, he can't quite articulate the what. But when he shares how he does things, I'm like, "Oh, that's a great strategy." Similar to your example earlier there, Jennifer, on taking the 1/4 and pushing it over. It's like, oh, you use the commutative property and the associate of property. That's fantastic.
I think when adults start to make that connection, like Jon, you were just saying, it's like, you've figured out strategies, which is great. It's awesome. But imagine if we could help all students figure them out sooner and not just land on them by chance through life. That would be so fantastic. I love it. Something I've done with parents when I go in schools and they do parent nights, sometimes I'll give them something maybe a little more challenging and then work our way backwards.
So, for example, giving them a proportion, say, a proportion on a double number line and parents can see it coming to life and almost have this epiphany for themselves, like, wow, that would've been really helpful to have when I was younger. And while I'm on proportional reasoning and the double number line and all the magic that happens there, before we wrap things up, Jennifer, I wanted to share one of my favorite resources is the Teaching Developmentally book, which has just released the 11th edition.
I'm not sure how it can get much better because it was awesome, but I'm sure there's some new nuggets in there that are definitely worth exploring. So, specifically for those who have ignored our suggestion over many podcast episodes to come and check out this book, it really does change how you look at things as mathematics gets more complex, especially for me understanding ratios, rates, proportionality. That has really shifted my own thinking. I know Jon has been on this journey as well.
So, we wanted to take a chance to share that with those who are unaware. Go check it out if you haven't yet. So many things to be learned in there. And, Jennifer, you are one of the authors of that series, and yeah, we appreciate the work that you're doing. So, before we wrap up, where can the math moment maker community learn more about you and your work around number fluency, fact fluency, and then all things, mathematics?
Jennifer Bay Williams: Well, I don't have a website, but I'm happy to engage. I'm at lots of conferences and I have been writing a lot. So, I feel like the ideas we've talked about are in the little purple book, Math Fact Fluency, and then the Figuring Out Fluency series that goes beyond basic facts. There's the rainbow book and then all the classroom companions full of activities. And then, this is just all things, teaching math and with a stronger focus on proportions, by the way, and fluency, and culture and language as well.
So many changes in this edition. So, I'll be at the NCTM annual conference and other places. I'm a professor, but as I have time, I do travel to districts and schools. So, I'm happy to engage in the dialogue anytime I can't.
Jon Orr: Awesome stuff. Thanks so much. We are also traveling to the national conference this September. So, hopefully, we can see you face to face there. We'll try to meet up with you, but thanks so much for joining us. And we look forward to chatting with you again.
Jennifer Bay Williams: Thanks, Jon and Kyle.
Kyle Pearce: Have a great day, my friend. We'll see you soon.
Jennifer Bay Williams: Yes. We'll see you in Los Angeles.
Kyle Pearce: Well, as always, math moment makers, you know Jon and I are big on finding ways to reflect that resonate with you, that work for you. So, how are you going to do it? How are you going to make sure that this information doesn't wash away like footprints in the sand? Are you going to write it down? Are you going to tweet it out? Are you going to put it on Facebook? Are you going to comment at the bottom of the show notes page on our makemathmoments.com website? Whatever you do, make sure that you are finding a way to reflect and maybe set a little mini-goal that you can apply in your practice moving forward
Jon Orr: In order to ensure you don't miss out on our new episodes as they come out every Monday morning, be sure to subscribe here on your podcast platform. Also, these episodes are visual, where you can watch us talk with Jennifer Bay Williams or all of our guests over on YouTube. You can head on over there to watch and subscribe over there as well.
Kyle Pearce: Love it. Math moment makers, you know that we read every review that comes in, whether it be on Spotify, on Apple podcasts, Google podcasts. When they come to us, our hearts are filled just like this one by JC Riley09. It says, "Must listen every week. It's a five-star rating. I'm a math teacher of 11 years. And this weekly show has evolved me into a better educator. The mix of experts, teachers, district leaders gives me multiple perspectives and experiences on how to make math learning better for the kids in the classroom. My lessons have become more engaging and my teaching practice has really pushed forward. So, awesome job there."
That was by JC Riley09. You are fantastic. That was on the US Apple podcast store. What country are you coming to us from? We'll take them in the United States. That's great. We got lots of them on there. If you're coming to a country like Canada, where we have less of those reviews or maybe you're coming from the other side of the world, make sure you leave us a rating and review.
That'll not only let us know that we're meeting the needs of educators out there, but it'll also tell Google and all those search engines that, Hey, this is a must listen podcast for educators.
Jon Orr: Show notes and links to resources and complete transcripts can be read from the web or download and take with you. Hey, head on over to the show notes page, makemath moments.com/episode197. Again, that's makemathmoments.com/episode197.
Kyle Pearce: While you're over there, hit that Tasks page and check out some of those problem-based units. Well, until next time, math moment makers. I'm Kyle Pearce.
Jon Orr: And I'm Jon Orr.
Kyle Pearce: High fives for us.
Jon Orr: And a big high five for you.
Sign up to receive email updates
Enter your name and email address below and we'll send you periodic updates about the podcast.
DOWNLOAD THE MAKE MATH MOMENTS FROM A DISTANCE CHEAT SHEETS
Download the Cheat Sheets in PDF form so you can effectively run problem based lessons from a distance!
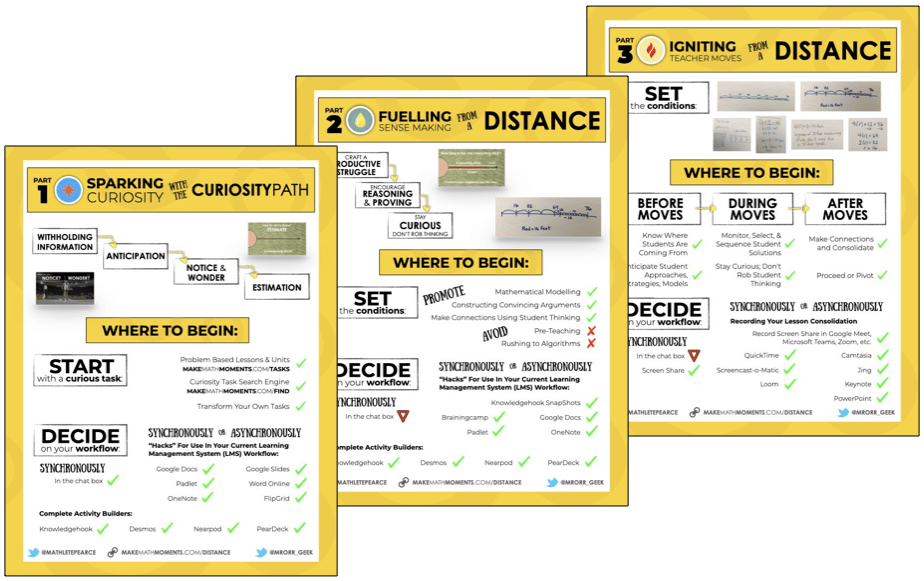
UP YOUR DISTANCE LEARNING GAME IN THE ACADEMY
There is a LOT to know, understand, and do to Make Math Moments From a Distance.
That’s why so many Math Moment Makers like YOU have joined the Academy for a month ON US!
You heard right: 30 days on us and you can cancel anytime. Dive into our distance learning course now…
Thanks For Listening
- Apply for a Math Mentoring Moment
- Leave a note in the comment section below.
- Share this show on Twitter, or Facebook.
To help out the show:
- Leave an honest review on iTunes. Your ratings and reviews really help and we read each one.
- Subscribe on iTunes, Google Play, and Spotify.
1 Comment
Submit a Comment
ONLINE WORKSHOP REGISTRATION
Pedagogically aligned for teachers of K through Grade 12 with content specific examples from Grades 3 through Grade 10.
In our self-paced, 12-week Online Workshop, you'll learn how to craft new and transform your current lessons to Spark Curiosity, Fuel Sense Making, and Ignite Your Teacher Moves to promote resilient problem solvers.


I am working with a 6th grade student who still counts on/back using her fingers for addition and subtraction and still skip counts (using her fingers to keep track of each set) for multiplication and division. How do I get her to move beyond relying on fingers? Teaching her doubles doesn’t seem to help as she always falls back to using fingers so it is like the strategy isn’t really a strategy.