Episode #211: What Should a Math Support Class Look Like? – A Math Mentoring Moment
LISTEN NOW…
WATCH NOW…
In this episode we speak with Laura Compean about the common struggle educators face when designing and facilitating a math support class to help students who have traditionally struggled with mathematics. How can we build a welcoming classroom culture that might help to heal bruised relationships with mathematics while ensuring that students are engaging in the learning necessary for them to be successful in their mainstream math class?
We will talk about this pebble in Laura’s shoe through this Math Mentoring Moment episode where we talk with a member of the Math Moment Maker Community who is working through problems of practice and together we brainstorm possible next steps and strategies to overcome them.
You’ll Learn
- Why mimicking isn’t enough when students reach higher mathematics courses;
- How we can bridge the strategies students are using in problem based lessons to the abstract math concepts;
- How to focus on fluency and flexibility to prepare students for algebra 1;
- How we should consolidate our lessons to make them most impact with students; and,
- What a math support class should look like.
Resources
Make Math Moments Problem Based Lessons & Units
Are you a district mathematics leader interested in crafting a mathematics professional learning plan that will transform your district mathematics program forever? Book a time to chat with us!

FULL TRANSCRIPT
Laura Compean: So they were doing amazing double number lines. They were making a table, everything that I was like, "Wow, you guys were right. This is so cool. They did come up with that on their own." And then we sit down and they start doing DeltaMath and they're like, "Oh, we have to do algebra now?" It's like you were doing algebra at the whiteboards. You just didn't make that connection. So what I feel like they're saying is that their algebra one class is that traditional... What they're doing in this class does carry over.
Kyle Pearce: In this episode, we speak with Laura Compean about the common struggle educators face when designing and facilitating a math support class to help students who have traditionally struggled in mathematics. How can we build a welcoming classroom culture that might also help to heal bruised relationships with mathematics while ensuring that students are engaging in the learning necessary for them to be successful in their mainstream math class?
Jon Orr: We will talk about this pebble in Laura's shoe through this math mentoring moment episode where we talk about the member of the math maker community, a person just like you who is working through problems of practice and together we brainstorm possible next steps and strategies to overcome them.
Kyle Pearce: All right. Let's do this. Welcome to the Making Math Moments That Matter podcast. I'm Kyle Pearce.
Jon Orr: And I'm John Orr. We are two math teachers from makemathmoments.com who together...
Kyle Pearce: With you, the community of math moment makers worldwide who want to build and deliver problem-based math lessons that spark curiosity...
Jon Orr: Fuel sense making.
Kyle Pearce: And ignite your teacher moves. Welcome everyone to another math mentoring moment episode where, yeah, just like John said, we get to hang out and chat with a math moment maker just like you about that pebble or pebbles, or boulder that might be kicking around in your shoe. Jon, today it was great getting to chat with someone who, first of all is wearing a ton of hats as you'll find out, and that's a struggle in and of itself, but is also entrusted to deliver a math support class.
They call it a math lab class in this school, and we get to chat about some of the challenges in doing so because you definitely have some competing priorities when you're in that particular scenario. What was your take from the conversation here before we dive in?
Jon Orr: Yeah, before we dive in, I was impressed with the name of the class to start with, math lab class. I think that's a pretty nifty way to call your support class or, "Hey, I'm in this class because I've been pulled aside. I needed help more than these other kids and so what a great way to name that class." I think Math Lab makes a lot of sense. I'm excited to take a math lab. That sounds kind of cool. But it was great to chat with Laura because she's on this great quest. She's on this quest. A lot of us are on about changing mindsets in mathematics and what a great way to start with supporting those students in her class and trying to get students who've probably routinely been told that they're bad at math. Hey, there Laura. Thanks for joining us, the Making Math Moments That Matter podcast. How are you doing today?
Laura Compean: I'm great. How are you?
Jon Orr: We're good. We are good and tired, but great.
Laura Compean: That's good.
Jon Orr: We're just coming off the weekend of the virtual summit at the time of this recording, so Kyle was just saying how old he feels and coming off basically staying at his computer for 12 hours, two days in a row and feels like he's hit a brick wall. So he's doing well, he's doing well. But we are happy to be here with Laura. Laura fill us in a few details. Where are you coming from? What's your teaching role? And what's going on lately?
Laura Compean: Great. Thank you. My name is Laura Compean. I am from Southern California, little city called San Clemente, California. I have been teaching at San Clemente High School for probably 18 years now. I actually graduated from San Clemente High School, so I didn't go very far.
Kyle Pearce: Ooh, there you go.
Laura Compean: I am currently a calculus and math lab teacher. I'm the department chair and I'm also an instructional coach. So I have many different hats going on.
Kyle Pearce: I was just going to say, I'm like that is quite the massive bunch of roles that you're taking on. I can only imagine that there's probably... Later on we're going to talk about pebbles in our shoes and I think the more roles you take on the more pebbles or boulders that you invite into your shoe.
Laura Compean: Exactly.
Jon Orr: Totally.
Kyle Pearce: I'm sure we'll have a lot to chat about here today. That's awesome. Laura, having teaching at the school that you went to, I want to know what is that? Do you feel a sense of additional pride? I think teachers all feel very proud of the school they teach at. They really want students to feel invited into the community. Do you feel like you have an added sense of that passion for the school or are you like, "I'm living in the same neighborhood?" What's going on in your head with that? I'm always curious.
Laura Compean: It's so amazing that I've been here so long that when I first started, I was teaching students that I was babysitting back five years prior to. And then now it's like, "Okay. Now I have students of my own classmates that I graduate with. Their kids are coming through." So it's funny having the different role... As I get older, there's more and more community that's coming back through and my nephew is actually in my class now, so it's a lot of fun. I definitely-
Jon Orr: Awesome.
Laura Compean: Definitely. My prom date is a history teacher here as well.
Jon Orr: Wow.
Kyle Pearce: That is hilarious. That's awesome.
Laura Compean: We all come back. It's a great place to live.
Jon Orr: It's a community.
Kyle Pearce: So people both should chaperone the prom and maybe put on a little skid or something for the new prom king and queen. There you go.
Jon Orr: Yeah. Awesome stuff. Awesome stuff. Laura, if you've listened to the podcast before this question is coming, we ask all of our guests this question. We are anxiously awaiting what your math moment is. So when we say math class, this image pops into our minds. These things kind of stay with you. Fill us in on some details there. When we say math class, what pops into your mind? What has stuck with you all these years?
Laura Compean: It's so funny that you asked. I've been thinking about this question for the eight months that I've been listening to your podcast and it definitely goes back to, I was in the movie theater after I graduated high school and my calculus teacher comes in. I was really happy that I actually passed the AP calculus class with the four... Sorry, the AP calculus test with the four and he's like, "Laura, I was so disappointed with your score." And it hit me like, "Oh, I thought I would make you proud."
It turns out I was mimicking the whole entire time and I fooled him to think that I was a lot smarter than I really was. It took me until I got to this past year that I was like, "Wow, I wasn't really understanding the material, I was just really good at practicing and memorizing everything that finally clicked at like, "Oh, I really did fool him. He thought I was smarter than I really was."
I mean, I worked hard. Don't get you wrong. I worked really hard on the problems. However, I don't know why it slapped me in the face when he said that to me. I now realize like, "Oh wow, I was mimicking the whole time."
Kyle Pearce: I'm guessing that you've heard us talk about that. We've had similar experiences myself in my later years in university sort of coming to realize that, "Oh my gosh, I don't really know what I'm doing." And only once I started teaching I went, "Oh, there's something wrong about this." And it's really set us on a little bit of a different path. So I'm wondering how does that moment impact your teaching practice now? Is it something that you put straight into practice right out of the gate or was it something that you only really thought about later into your career?
I know for me it was much later when I started to realize what was happening, why some of my students were struggling and why other students who were seemingly getting good marks on a report card, but yet they still didn't feel confident that I could never understand that. I'm like, "You have an 85. How is it possible that you don't feel confident?" It all makes sense to me now. How do you think that's impacted or influenced how you are as a teacher now?
Laura Compean: A hundred percent. Like I said, this has been very new to me to be able to see that difference of how many kids truly are just memorizing the types of problems and how many of them are actually understanding it behind it. I am excited. I remember for many years in the past I would always say, "Oh, don't worry. This one is not on the test. Or oh, don't worry, this will look exactly the same on the test."
Kyle Pearce: "Or hint, hint, there's going to be something like this on the test." I did that all the time.
Laura Compean: How many times have I said that? Absolutely. So now I'm like, "Okay guys. I want you to look at the big broad aspect of it. Do you understand? Can you explain to me what's going on here?" And having the kids turn and talk to each other is so much more valuable of what I can hear them saying if they really understand it or not. Or are they just like, "Oh, that's what the teacher said, but they don't know the why's behind it."
With AP calculus, I think a lot of it is conceptual that they need to know that and that's where the class gets so hard that they can't just memorize everything. It's been huge, huge shift in my own teaching. And like I said, I've been here for 20 years and I'm like, "Wow, I've definitely messed up." Not messed up, not messed up. Just had a different approach.
Jon Orr: Right.
Kyle Pearce: You know better now. The more you know. Right?
Laura Compean: Yeah, for sure.
Jon Orr: Laura, can you share us a success story from this pivot that you realized you said in the last year to realize that you've changed your teaching style to go away from this? Give us a snapshot. What would you say as a big win or a success story from this change?
Laura Compean: I remember back in... It was before the AP test, so probably March or April, I started using a lot of the Math Medic or Calc Medic material for the volume and area type of problems for that unit. I started giving them the experience first, "Here's a pair. Can you find the volume of that pair?" Or it was a lot more and I put them in groups of three. They were working together trying to experience and the majority, I would say 85% of them loved that method because they could actually understand what was going on. It wasn't just me telling them the formula.
They could really discover it on their own. But I remember the smartest kid in the class, he would come in, he is like, "Why are you doing this? You need to just tell me what's going on." And I'm like, "No, no, no. You can do it. I believe it. I believe it." And so finally at the end of the year he's like, "That was really the hardest part of the whole entire year. However, I will always remember that volume in the area type of formulas." And I was like, "Yes."
Kyle Pearce: I love it. I love it.
Laura Compean: So it's funny how the smartest kids, they love just being told how to do the math because they've never been asked to think and it's super cool to actually get them to think about it.
Kyle Pearce: I love it. I love it. I've had many experiences like that and oftentimes it's like pushback initially from some of your "top students". Right? I wanted to comment on this earlier as well. You had mentioned that you were a memorizer or a mimicker but you still worked really hard. I will give them that. You can't just mimic your way through without working hard. It's hard work to do that to put the reps in, but the difference though is it's almost like you almost don't have to be thinking about it. You just keep doing it over and over again and eventually it's like muscle memory when you see that sort of thing.
Jon Orr: It's different thinking. It's not like this kind of problem solving thinking. It's kind of like a puzzley thinking. What I mean by that, I feel like when I have my senior students who have traditionally been mimickers, you can mimic to a certain point, but then you know that the students have to be able to apply that. And you may show them along the way how to do a lot of those things because we were teaching mimicking. But then there was a point where a good group of those students had to do some thinking there to connect some dots because we were like, "Oh yeah, I'm going to give them this question."
It's a different thinking because we still front loaded everything. And then we asked them to think about how to take what we front loaded and then fit it into this mold, which is a different style of thinking than I think us going like, "We don't know what we're doing here or we're not going to tell you exactly what to do. What do you think? What's the first step here in this? What do we have on our tool belt from prior knowledge to use in this new situation?" I think that's a different style of problem solving.
Kyle Pearce: Yeah. When you're mimicking, you are relying a lot on that quick thinking brain and then eventually when you change something, it's sort of like you go, "Whoa," and you have to knock them out of that for a minute and then they go, "Okay, now I've got to think about this a little bit," which students typically, humans in general are not huge fans of Right? As having to think and work hard. But ultimately at the end of the day, it's like, I used to, in my mind picture a good math student was someone who put in those reps.
And I think you still need reps. You still need to practice and you need to work hard. But it's just how we get to that place. I want to make sure that students aren't just blindly following along. But I do want them to get the reps so that, hey, some of this stuff is going to almost be second nature where they see a problem, they're like, "Oh, I know what to do here. I don't need to think about this one." And now I can think about something more complex but not because they blindly got their way there.
So really interesting discussion here, but I'm wondering... I want to shift now to what's on your mind lately. We had already talked about you're wearing a lot of hats so I'm sure we could probably spend a whole week talking about the different pebbles that appear in these different scenarios. But what's the one that's keeping you up at night right now? The one that's on your mind and that maybe we can kick around here today and see if we can't wiggle it out there.
Laura Compean: Great. Thank you. So I have this math lab class, which is the current freshman, current ninth graders who did not do well in math eight. So we pulled them in and they have two math classes now. There's an algebra one that every student needs to pass to get out of high school and then they're also in math lab. In the past we've given it to new teachers where, here you do what you get. So it's been a really hard class for not only behavior wise but getting the kids to do math.
And they've always been a concurrent class where, okay, in algebra one they're doing this. So in math lab they're going to be just hammering in more. And so it's been really hard on the kids because if they already don't like math and now they're doing two math classes essentially and one day, it's a lot. So I have been working in the past summer trying to shift it and make it into more of a confident booster class that they can enjoy math, that we're doing a lot more games like mathematical thinking games that we're trying to build their foundational skills so they can be more successful in their algebra one class.
However, I'm having a hard time getting them motivated, getting them thinking, trying to get them to even start a problem and that's where my pebble is. I don't know how to motivate the students
Jon Orr: The age old question. Laura, paint us a little bit of a picture of the class. So you've said that you're trying different games. You're bringing different elements in. You want it to be kind of a motivational kind of class, but also a confidence builder class. I think that's great. I think that's a great pivot to probably just saying like, "Hey, you're doing solving two-step equations in algebra one and we're just going to do more of that. Longer and more repetitions." Right? So I can see why you might want to pivot and I think that's a great opportunity to change some mindsets with these students. Paint us more of a picture of what say right now a typical lesson looks like for you.
Laura Compean: Okay. We have been doing a lot of would you rathers, which one doesn't belong? Something at the beginning of the lesson, if it's a journal. We've done a lot of Jo Boaler's with the growth mindset, trying to get them writing and speaking, and talking mathematically without them knowing it. We've done a lot of your lessons with the notice and wonder first and then setting them to the whiteboards to get them thinking about how to solve the problem. That has been great. We've tried spicy, medium, and mild type of problems.
Jon Orr: Ooh, I like that.
Laura Compean: And just giving them the choice on which questions to go and choose. It's funny 'cause I think everyone would want to do a mild and they sometimes jump straight to the medium and they're like, "Look, we can do it." I'm like, "Well, now it's time for you to try the spice." We're constantly having them up at the whiteboards and working in groups of three." I know that whole low floor high ceiling is super, super important more so than I've ever realized because if they feel intimidated by any means, they just shut down. So I don't know how to get the right entry point for them to start at the beginning once we introduce the problem.
Jon Orr: Those all sound like great activities. So I guess my next question is what are you seeing from the students that makes you sit, think right now what I'm doing isn't engaging them.
Laura Compean: Myself and then I have a student teacher in here. So I thought if there's two teachers we can double team them. We always have to be standing next to the team to actually be engaged and start doing something. My envision is that we can send them and they can start right away without us needing to be like, "Okay, what's the next step?" Leading questions. And there's not enough of us to still be at six different boards at one time. So I would love for them to be able to start on their own and sounds weird but excited to do the problem.
Kyle Pearce: It sounds weird but it's not 'cause it's exactly what we're aiming for. I got a question kind of going outside of this class. I have a vision in my head, maybe a bit of an assumption here that these students have come in. It's called a math lab class. In reality, if they're in this class because they've struggled in the past with math, my guess would be is that they know that they have struggled with math and so they have probably told themself a story or maybe their grades have told themself a story or maybe even the actions of parents or teachers or whoever or maybe even other peers may have sort of told them this story that they're not so great at math.
So that's a big hurdle right there. Just right out of the gate, no matter what we do, there's this image in their mind potentially of what they are either capable of or not capable of in a math classroom. I'm wondering, so they go to this math lab class and then at some point in the day they also go to algebra one. My wonder is what does algebra one look like if you were to paint a picture? Because you're kind of like, "I'm going to this math class and I see that my teacher or teachers are really trying to engage me and get me in and all these things."
And maybe there's even some success. It's like, "Wow, that was a great lesson. I learned something." And then I go down the hall later, maybe after lunch and then I go into the algebra one class. What is that math class or what message does that math class send them?
Laura Compean: Yeah. They are building. They are definitely building. It's typically a, "Here's the notes. Let's do some practice problems and then here's your homework." So I'm trying to spread the same experience. Let's have the kids grapple with it. It's pretty interesting I've had a couple of the kids, we are up at the whiteboards. We are doing, I forget which activity that you had. The plant growing one?
Kyle Pearce: Oh, cool. Yeah. Planting flowers revisited.
Laura Compean: Yeah, doing the equations, right? Two-step equations?
Kyle Pearce: Yeah.
Laura Compean: So they were doing amazing double number lines. They were making a table, everything that I was like, "Wow, you guys were right. This is so cool. They did come up with that on their own." And then we sit down and they start doing DeltaMath and they're like, "Oh, we have to do algebra now?" And it's like, "You were doing algebra at the whiteboards. You just didn't make that connection."
Kyle Pearce: Totally.
Laura Compean: So what I feel like you're saying is that they're algebra one class is that traditional, here's the notes. The teacher is telling me what to think and then I'm going to mimic the same type of thing that we need to figure out what they're doing in this class does carry over into the other class.
Jon Orr: Right. It's almost like thinking about what's the bridge? What's the bridge that takes what we did in the planting flowers and how do we connect that to what they're doing in the other class where they're going to get their grade and it's the thing that they have to pass, and they're more worried about that maybe knowing they're in this class. And so what is that bridge so the student can say, "Today, actually is going to help me in both classes? I was feeling successful here but I realize now that, that strategy, that model that I use to solve that problem I can use to solve this problem over here." What do you see right now as that bridge?
Laura Compean: Honestly, I don't know. Maybe more of the hands-on type of activities, creating more of the story problems. Not just the word problems from the book, but how can we use that planting flowers type of strategy in the algebra one class so they're not just solving two X plus five equals three over and over and over again. I don't know.
Kyle Pearce: I have two wonders slash thoughts that I'm thinking about here and there's one. One, I'm in a perfect world. I'm envisioning... Imagine you did that planting flowers revisited unit. For those who have never used it, it's basically like doesn't notice and wonder. It shows this sunflower starts at, I think it's four centimeters tall. And then a week goes by and then it grows a little, and then it grows a little more, and it grows a little more.
So it's this linear relationship being developed and students obviously out the gate may or may not realize that. They generate an equation. They solve it. We try to promote using the tools like a double number line or a table or a graph. And in my mind, I'm wondering, imagine a world where if you knew what was going to be coming up topic-wise in algebra one, let's say in a perfect world your class would be the morning and then algebra one would be maybe the afternoon, and you're like, "I know today they're going to introduce two-step equations."
So you give them the thing that maybe isn't happening in the algebra one class. And it's almost like by the end of your class, we consolidate it. They share their strategies. But then you take that intentional 10, maybe 20 minutes to go, "This is exactly what this looks like algebraically in case they missed it." Right?
Jon and I just recorded an episode about the oblivious viewer loop where it's like someone watches a show and they missed it, someone missed the point and the person next to them was like, "How'd you miss that? It was right there." We make it super explicit. And later today you're going to be looking at a couple equations like this and maybe you give a couple of the equations. You go, "Pretend that equation is this flower. What would it look like?"
You're setting them up to go, "Okay. They got this experience." And now it's like later today that teacher may just come out and say, "Here's what a linear equation is. It's Y equals MX plus B and there's the coefficient here. Whatever we do and I did it, I totally get that might be how it's being presented. But imagine if they had that sort of under their belt and consolidated so that when they walk into that class they're going like, "That's the flower." And in their mind they can see how it's growing or they can maybe make a new context to get that maybe headstart on that concept. When I share that, is that even a potential possibility? Is that way too from the movies or in my dreams, that sort of thing happening?
Laura Compean: So there are quite a few grade levels behind in their math. Originally, we are going to just do puzzles. We're going to do patterns and notice and wonder. All the things that they're missing. We did a lot on the multiplication of two-digit numbers using a area model. Because my envision was to use that into factoring second semester because they're terrible at factoring polynomials.
So we tried to keep up with the algebra one class, but they're so far behind that we couldn't do it effectively. So after the two-digit numbers multiplication, we went into linear relationships. So I think what you said is amazing, that would be ideal. But we can't keep up what we spend a whole two weeks on. Algebra one is already off the race.
Jon Orr: Right. Now going back to what Kyle's recommendation was in the sense of trying to give them a leg up before they go in there. But if we still take some nuggets from his recommendation there, but at the end. So I think this is the situation that I've used to find myself in, and this is related to the oblivious viewer effect that we mentioned in that last podcast. Actually I think it's coming. It hasn't been released yet, Kyle, is that I was teaching my lessons when I started switching to teach more activity based like you described.
I used probably every single activity that you just listed off there. And I did have a lot more engagement in my classes. I had kids liking math a little bit more, but I think what happened was, and I was teaching say these problem-based lessons and I was having students enjoy math class, but at the end of math class came and when I had to give them, we call them the naked problems, the problems that are just X and Y's or they had a hard time, and that ended up being what the standardized test was and they went to grade 10. That's what they saw in grade 10 and felt like they weren't being successful there.
It wasn't until Kyle and I had chatted about this that we realized that we had to tie that bow on. We had to say, "We do need to build this bridge between these great activities that bring out models and strategies and then show kids how to use those models and strategies on the naked problems."
So it's like we did our flipped classroom idea where instead of front loading, we taught through the problem-based lesson to bring out the ideas, the strategies, the models. They developed them. We consolidated and then it was like, "Okay. Now, we're going to solve this problem." I did a little bit more teaching at that point, but taught using the strategies we saw from the kids or that was brought out already. So it was feeling like we took and tied what they did and we made sure that those strategies and models came out, but they felt ownership in those. And then we tied it to go, "Oh you know what? On this two-step problem, that looks like this. We're going to use that same strategy here and we'll draw the same model here."
We connected the dots. And so kids then once we started doing that and then making it very clear at the end, "Our learning goal today was to solve these two-step equations. We did that by doing this, by doing this, and by doing this. We want to continue to do that and that can be helpful to solve these problems." A lot of times we would make an anchored chart together based off that so that we said, "Hey look, this is the strategies and models we used to solve this skill. Insert skill here." Whatever that skill is.
But the big story here is that for a long time we thought engagement would get them, and then what Kyle said, we thought by putting them in this situation that kids would pick up what we're putting down. But it wasn't until we purposely said, this was our learning goal. These are the expectations. These are the look-fors. These are the success criteria we're looking for. All of a sudden, we had some better success moving forward.
Laura Compean: I think that's exactly what I'm missing is I'm not tying it together what you said about the bow. We're not tying the bow on yet. We're still just doing all these different activities and kids are even saying, "We're not doing anything that we're doing in our algebra class." And I'm like, "Oh, that should be it."
Kyle Pearce: But we are.
Jon Orr: Right. And that's the perfect opportunity to say-
Kyle Pearce: But there's more.
Jon Orr: ... "Wait, five more minutes."
Kyle Pearce: Yeah, "Wait, there's more."
Jon Orr: This is. Let's go through why this is the case after you've brought these ideas full round.
Kyle Pearce: Honestly, today I was in a class. I was in a grade eight class and I was doing some algebra on a number line. At the end, everyone had the answer and it's in your mind. Your brain is telling you what's the point in restating it? But at the end of the day it's like, "Okay, I want to gather them around." So I gathered them around aboard. It's almost like you ask them a question about it. Turn and talk. It almost lets you get your script together in your mind of exactly what you want to say. And it's almost like you just have to say, "I just need eight minutes of your time and it's going to be well worth it."
It's like, "These are the important eight minutes that I need your attention for and I want to make sure you jot that down because later today or this week, or whenever it's coming up or last unit, if that's the case for the algebra one, this is what we did today and this is why we did it." And helping with that, being that explicit can be really helpful. And then I want to also flip back just as a thought because you had mentioned something that got me, which I know I'm picturing myself being in this place.
You had mentioned about how students had missed a lot well before algebra one. So there's the other option. You go back there, but again, it's almost like if it's so far back that it's not going to help them in that algebra one, then you have to make a choice. And maybe it's a choice for this group and maybe the choice is different for the next group, but it's like where do you want to go? Because maybe you're making gains here, but if it's so far off from that algebra one and then next year, I mean, I guess the question you have to ask yourself is what's the true purpose of that class?
And my gut is telling me that maybe for you the purpose is you want kids to realize that they can think mathematically, that they have a lot more to offer than maybe they thought in a math class. All of those amazing things. But I'm guessing that the reason it's actually in their schedule is as a means to help them get through the algebra one.
Laura Compean: Correct.
Kyle Pearce: So it's hard because there's competing priorities here and the word priority is actually only supposed to be a singular word. It's actually not supposed to ever be plural. Priority means primary, one, the thing. And it's almost like trying to figure out what would that be? And I guess in my mind, if it is to try to support them in that algebra one to ensure they can get through that algebra one and get that credit, the reality is this class probably should exist in grade one and it should exist in grade two and grade three all the way through so that we catch students way earlier than algebra one, but not a perfect world.
So here if I can create that bridge, like Jon had mentioned that bridge from where you can get them to engage in the problem and they can access it. And then I just sort of like that bow tying at the end is almost like, "How can I let them see that these things are the same?" It's almost like you have the secret sauce. You talked about the spicy, medium and mild. You have the secret sauce to help those students get to the more algebraic or abstract representation in that algebra one class.
So I don't know. Where's your head at there? Does that seem like something that might be attainable or something that you can work towards and might help those students a little bit in that algebra one?
Laura Compean: Yeah, absolutely. So it is supposed to be a helper for them to pass algebra one. When I started this in the summer, I'm like, "Okay, what are the most important concepts that they have to know and be good at, so I'm not going back to fifth grade math?" Yes, they need to know their multiplication facts, but I don't want to just drill them over and over. Like I said, the fact the area models for the two digit multiplication was not supposedly to go back to whenever they learned that in whatever grade. So we can look forward to the factoring later on to be like, "Hey, we did this with algebra trials. We did this with the area model."
Kyle Pearce: And they get kind of both of those things, right? Because they get to practice that multiplication with that model, even though now you're moving on to more algebra with variables involved and so forth.
Laura Compean: Right. So I think my big question also is what curriculum should we be covering during this? Because it's so open-ended. We are almost like every week, "Oh, what's today?" We plan on Fridays and, "Okay, what should we do next week?" And we adjust it as we go. But it would be nice to have one set of these are... And it's hard for every school, every kid is different.
Kyle Pearce: My gut is telling me from the curriculum standpoint, if you were to take that algebra one and you looked at here's what the algebra one is and if you could go what is just below there? What is just before it? And what's the low floor high ceiling thing I can do there? And if they can enter that, that gets them to that point like that bridge to the next thing. So it's not that they have to know the algebra one stuff when they leave your class, but imagine if I am going to be doing factoring for example.
So you're factoring trinomials. I might start with that two digit in that class and I might just try to bump them towards throwing like, "Hey, it's a 10 squared instead of an X squared." And it's, "Oh, there's a three 10s instead of a 3X. And you could just get them to get to the place just before. And it's like if they can enter into just before, then at least they might be able to do that little step up in that algebra one class to see that, "Oh my gosh, what I did in that class is actually helping me in this class." Instead of them maybe thinking it's like, whoa, it's so disconnected in their mind that they don't see it as actually supporting.
Jon Orr: And I was going to add, if I was going to design that course too, I do exactly what Kyle said, but I would focus everything on strategies that scaled. So models that scale, strategies that scale. You used the area model there, which is perfect, right? You want to use the area model for multiplying two digit by two digit or multiple digits because it will scale into the algebra like you've realized. But when you're multiplying fractions, the area model is also great for that same thing.
So we could build in multiplying of fractions to re-enhance that same model can scale. We can use the same model here. When you're adding fractions, we'll focus on fluency strategies. Strategies about how numbers work and thinking about decomposing components and then realigning them and adding in different ways because that can be helpful with collecting terms.
And when we go to add expressions instead of multiplying expressions. I would think about trying to find great strategies that are supportive for that particular skill, but more than one skill. So for example, this book right here, Figuring Out Fluency from Jennifer Bay-Williams is a great resource for that because they show the different strategies using number lines and different ways to think about number that scale up the ladder.
This is a K to eight book, but Kyle and I actually, we were reviewers for the middle school book., I think it's specifically order of operations, fractions and proportions, and solving equations. So it goes basically into algebra one. Some of those skills. And the book focuses on what fluency strategies. If I was designing that I would spend a ton of time kind of doing the games and the strategies from there.
Laura Compean: Oh, that's fun.
Kyle Pearce: Okay. So I'm wondering, it sounds like you've got a few things to think about, maybe some potential next steps there. How are you feeling right now? How do you feel thinking forward? I know that you're heading into a bit of a break with Thanksgiving coming up here. Where's your head at? Let us know. How's that pebble feeling bigger or smaller at this point?
Laura Compean: I want to say thank you because I think just talking it out, knowing what the amount of work we've put in this semester has definitely shown that we're on the right track, being more intentional about wrapping up the lesson that we're doing and really specifically saying this was our learning target today. And maybe even asking them when have you seen this in your algebra class? Maybe we could have them bring it out and have it in kids speak. It's so much better for the kids to hear than always the teacher talking to them.
Jon Orr: That's great saying like, "Hey, we use this area model. Where do you see that?" And that might fit in this place. Or we use the number line here. Where do you see that might fit in? Or we used a having strategy and a doubling strategy. How might that see that fit in? So those are some really great takeaways. I think it's going to be awesome for you moving forward. What do you say on revisiting this? Coming back and say maybe before the summer or right after the summer.
Laura Compean: Sounds great.
Jon Orr: Talking about see how things changed.
Laura Compean: Yeah, I would love that.
Kyle Pearce: I love it. I love it.
Jon Orr: Awesome.
Laura Compean: All kids engaged, right?
Kyle Pearce: That's awesome. That's awesome. I mean that's why we love doing these episodes. I think anytime we have an opportunity as humans just to talk it out with somebody else, get a varying perspective, it gives you just something new to think about. So it sounds like your head is in the right place, which I think is most important. So you have the best in mind for those students and it sounds like you're doing a lot of really great things. And let's be honest, you're in a tough spot. They're getting additional support probably eight or nine or 10 years too late.
This is probably something that would've been really helpful, like I said really early on to try to catch those students before things get too far behind. And now, you're in a position where you're trying to do a lot of things. You're trying to help them with a lot of things from the past. You're trying to keep them doing the things now and you just have to also just remember to give yourself grace. And that is a tough challenge. So trying to have that balance between the two I think is really key and it sounds like they've got the right person in the position for it.
Laura Compean: Thank you. I appreciate that. Me and my student teacher, we talk all the time after they leave the class and we're like, "Okay. Well, we can't change in the three months that we've had them so far." Right? It's been a lot of bad habits in their past, so we just have to take it one day at a time.
Kyle Pearce: Absolutely.
Jon Orr: One day at a time. That's exactly right.
Laura Compean: Yeah.
Jon Orr: Awesome stuff. Thanks so much, Laura for joining us.
Laura Compean: Thank you, guys.
Jon Orr: And as I said, we'll look forward to our next chat.
Laura Compean: Absolutely. Get some rest.
Kyle Pearce: Have a great one. Enjoy the Turkey.
Laura Compean: Thanks. Bye.
Kyle Pearce: Take care. As always, both Jon and I learned so much from these math mentoring moment conversations and actually just after Laura, and we hit the stop button, she had just mentioned it's just great to be able to have a conversation, let the ideas flow and really just chat them out with somebody else. So how are you going to engage in some of that reflection?
Laura got to reflect and gain some different perspectives through this conversation with Jon and I here. How about you? Are you going to reach out to a colleague or a friend or a partner or maybe you want to go out to social media, leave a comment on our Facebook group or leave a comment on the YouTube channel for us to get a sense of what's happening. Maybe we'll get a conversation started over there. Whatever you choose to do, make sure you do something so that you take what you've learned here and you cement it a little bit by writing it down and making an action plan for yourself.
Jon Orr: Yeah. Awesome stuff. Love to hear what you've done there to solidify those ideas. Also, if you have not yet done this and you've not yet subscribed to the podcast, you should do that immediately. And then if you could, we would kindly ask, hit the review button. Leave us a review on that platform that you're on right now. Tell us all the ways that you've enjoyed the podcast if you've listened to more than once.
Now, if this is your first time, we would just love for you to subscribe and then keep listening. But if you've listened a few and you've gotten some value, leave us a review. That helps the show. It helps other math educators who are interned then helping students. So do us a favor, do your students a favor, do the world's students a favor. Leave a review. Thanks.
Kyle Pearce: Awesome. And friends, this was a math mentoring moment episode. We don't just randomly pick people here. We need to hear from you. So head to make mathmoments.com/mentor. That's makemathmoments.com/mentor, and we have a very short form, just like your name, your email, and essentially a couple sentences to describe what is the current pebble in your shoe? What's that thing that is keeping you up at night about math class or school in general? We'd love to have you on for a conversation just like we had here with Laura.
Jon Orr: In order to ensure you don't miss out on new episodes as we publish them every Monday morning, be sure to subscribe. I already asked you to do that. You can go ahead on over to YouTube as well and subscribe over there because this episode is also over there on video format in YouTube.
Kyle Pearce: I love it. All right, my friend. Show notes are always up on the makemathmoments.com website. This time it's episode 211. Holy smokes, that's episode 211. So makemathmoments.com/episode211. Well, until next time, I am Kyle Pearce.
Jon Orr: And I'm Jon Orr.
Kyle Pearce: High fives for us.
Jon Orr: And a high five for you.
Sign up to receive email updates
Enter your name and email address below and we'll send you periodic updates about the podcast.
DOWNLOAD THE MAKE MATH MOMENTS FROM A DISTANCE CHEAT SHEETS
Download the Cheat Sheets in PDF form so you can effectively run problem based lessons from a distance!
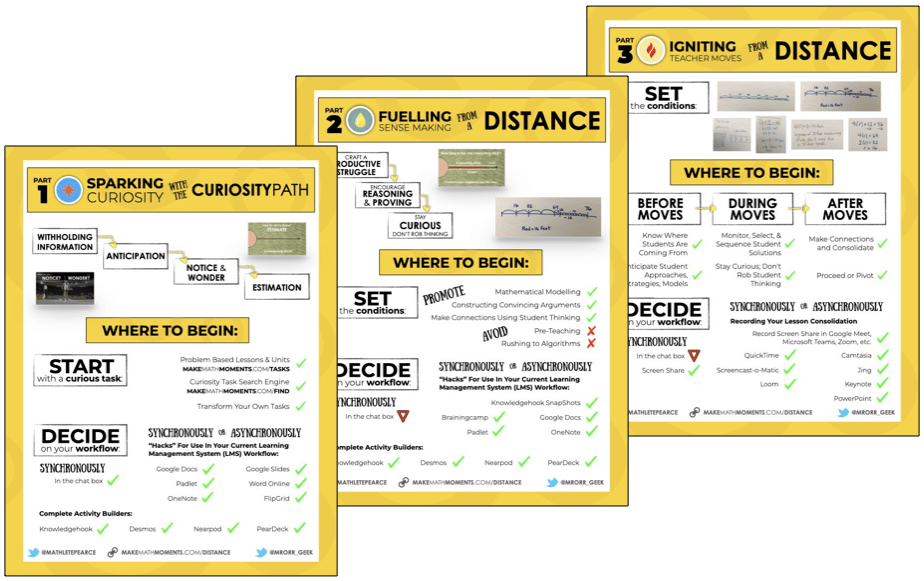
UP YOUR DISTANCE LEARNING GAME IN THE ACADEMY
There is a LOT to know, understand, and do to Make Math Moments From a Distance.
That’s why so many Math Moment Makers like YOU have joined the Academy for a month ON US!
You heard right: 30 days on us and you can cancel anytime. Dive into our distance learning course now…
Thanks For Listening
- Apply for a Math Mentoring Moment
- Leave a note in the comment section below.
- Share this show on Twitter, or Facebook.
To help out the show:
- Leave an honest review on iTunes. Your ratings and reviews really help and we read each one.
- Subscribe on iTunes, Google Play, and Spotify.
ONLINE WORKSHOP REGISTRATION
Pedagogically aligned for teachers of K through Grade 12 with content specific examples from Grades 3 through Grade 10.
In our self-paced, 12-week Online Workshop, you'll learn how to craft new and transform your current lessons to Spark Curiosity, Fuel Sense Making, and Ignite Your Teacher Moves to promote resilient problem solvers.


0 Comments