Episode 221: Celebrating Black Voices From The Math Moment Maker Community
LISTEN NOW…
WATCH NOW…
In this compilation episode of the podcast in honour of Black History Month, we highlight conversations from six educators from the Black Community that have had a significant impact on our pedagogical practice as we continue our journey to craft a more culturally responsive, inclusive and anti-racist mathematical community for all students to thrive in.
Stick around and you’ll hear Beatrice Moore Luchin speak about creating a culturally relevant and culturally responsive approach to teaching mathematics, Marilyn Strutchens’ approach to teaching tasks with multiple entry points; you’ll hear about the importance of learning goals from Dr. Ayanna Perry; why kindergarten math matters from Isis Spann; Dr. Nikki Newton shares insights and practical lessons on why counting is more than just 1,2,3; Pamela Seda shares key insights from her book Choosing To See; and Tashana Howse shares how to provide equitable support to students.
You’ll Learn
- How to create a culturally relevant and culturally responsive approach to mathematics instruction;
- How to create, find and use tasks with multiple entry-points;
- What a learning goal is and how you can write intentional learning goals for your students;
- Why Kindergarten math matters along with the strategies, tools and resources that will prepare your students for success;
- Why counting is more than 1, 2, 3 by learning about the complexity of the counting trajectory;
- How you can use a framework to build an equitable mathematics community; and,
- Equitable teaching practices and how you can implement them in your classroom daily.
Resources
- Episode #140: Math Is As Important As Reading – An Interview With Isis Spann
- Episode #62: Learning Trajectories & Running Records: An Interview with Dr. Nicki Newton
- Episode #207: Choosing To See: An Interview with Pamela Seda
- Episode #183: Ensuring Equitable Supports for Students – An Interview with Tashana Howse
- Beatrice Moore Luchin’s Summit Session on Creating a Culturally Relevant and Responsive Approach to Mathematics Instruction
- Using Multiple Entry Level Tasks To Support look next line
- Marilyn Strutchens’ Summit Session on Using Multiple Entry Level Tasks to Foster Mathematical Reasoning and Sense Making
- Ayanna Perry’s Summit Session on What’s a Learning Goal and How Do I Write One?
- Access the Full Virtual Summit + All Academy Courses and Problem Based Units for 30 Days Free
Take our Grow Your Classroom or District Math Program Assessment!
Get Your Customized Math Improvement Plan For Your Classroom or your School/District!
Take the 12 minute assessment and you’ll get a free, customized improvement plan to help you shape and grow the 6 parts of any strong mathematics program.

FULL TRANSCRIPT
Kyle Pearce:
In this compilation episode of the Making Math Moments That Matter Podcast, we are honoring Black History Month, where we are going to highlight conversations from six educators from the Black community who have had a significant impact on our own pedagogical practice as we continue in our very long journey to craft a more culturally responsive, inclusive, and anti-racist mathematical community for all students to thrive in.
Jon Orr:
Stick around and you’re going to hear Beatrice Moore Luchin speak about creating a culturally relevant and culturally responsive approach to teaching mathematics. Marilyn Strutchens is here to teach us about her approach to teaching tasks with multiple entry points. You’re going to hear about the importance of learning goals from Dr. Ayanna Perry, why kindergarten math matters from Isis Spann, and Dr. Nicki Newton shares her insights and practical lessons on why counting is more than just 1, 2, 3. Pamela Seda is here, shares key insights from her book, Choosing to See, and Tashana Howse shares how to provide equitable support to students.
Kyle Pearce:
My goodness, what a lineup. Lots of awesome key takeaways. And friends, if you hit the resources section of today’s episode podcast page, you’ll be able to go watch the full sessions of these summit sessions. So tons to learn here. Let’s do our awesome compilation episode. Here we go.
Welcome to the Making Math Moments That Matter Podcast. I’m Kyle Pierce.
Jon Orr:
And I’m Jon Orr. We are from makemathmoments.com, and together…
Kyle Pearce:
With you, the community of Math Moment Makers worldwide who want to build and deliver problem-based math lessons that’s spark curiosity.
Jon Orr:
Fuel sense-making.
Kyle Pearce:
And ignite your teacher moves.
Welcome, my friends, to another episode of the podcast where we get to celebrate some amazing voices from the Black educator community. And my friends, tons of learning here. These little snippets, you’re going to get little key nuggets, key takeaways that you’re going to really think on, and if I was you, I would definitely dig into some of these whole virtual sessions that we have from our past summit back in November 2022.
Jon Orr:
Yeah. So the clips that we’re pulling are from past conversations that Kyle and I have had either with the speaker or they’re from our just recent Virtual Summit, which happened back in November of 2022. So we’re pulling snippets from those sessions and putting them here so that you can also learn alongside these educators, just as we have over this last year. So let’s dig in here. We’re going to not waste any time. Our first speaker here, from the Virtual Summit this year, is Beatrice Moore Luchin. We’re going to talk all about creating culturally relevant and culturally responsible approach to teaching mathematics instructions. Here we go.
Beatrice Moore:
Where am I? I’m your student. Where was I in your curriculum? Was it just a focus on mathematics or did I see myself as someone who could do mathematics? Did I see myself as a mathematician? Did I see [inaudible 00:03:39] with the everyday problem-solving? Maybe with some of the historical pieces that you introduced into the classroom, was I there? As you are teaching mathematics, is my history and my culture being included? So again, let’s just think through these questions, and we’re hearing this from the voice of the student.
Was I in the curriculum? I’m your student. Where was my history? Where was my culture? You know, I have had posters and put them up in the classroom, and many, many years ago, it was more difficult to find, but now, because of the internet, it’s a little easier. But a lot of times, when we buy posters or we come across things about famous mathematicians, do they look like the students in our classroom? So while we owe it to our historical figures, yes, very important not to forget them, but we have some contemporary people who are successful who look like the students that we serve.
Where was the connection between my background and experience and what I was learning? Did I just learn math for the sake of learning math, or did I have connections between the math that I was learning and who I was as a person, where I was from, and even the things that were interesting to me? What does it mean to be culturally relevant? To celebrate and to leverage our knowledge, to leverage our cultures, to leverage our interest. Inherent brilliance. Our children are brilliant, and we have to start to speak life into that brilliance because that’s what it means to be culturally relevant. They come to us not empty, but full. They… the algorithms, not knowing the vocabulary, not knowing some of the formal things that we have decided that says that you are good at math or you are not so good at math.
Yeah, was there room for these things? What space did I have as a student to learn and to talk about equity and inequity, both inside my community and in the world? You see, when we teach mathematics, mathematics should be a tool that I’m teaching my students to use to navigate through this world and also to make the world better, for me, for my family, for my future, because it is… They get it. And so I owe that to my students. So what does it mean to be culturally relevant? It means that the voices of the children are present. And not only are the voices of the children present, but I’m listening to them, I’m forming relationships with them, and I am making sure that these questions that I have here, if not all of them are answered, many of them will be answered in a positive way.
And also, was there room to develop skills and agency to critique our social context, to understand the histories and the policies that were contributing to those realities? You see, our students have realities.
Kyle Pearce:
All right. Next up, we have a snippet from Marilyn Strutchens, who’s going to be taking us through problems and tasks where there are a variety of entry points for all students. Here we go, digging in with Marilyn right now.
Marilyn Strutchens:
So I believe that one way of doing this is multiple entry level tasks. They allow for multiple entry levels where everyone can make and start, where students may approach the problem in multiple ways. And I also think of multiple entry level tasks as a cheap way of differentiating instruction, because students can enter the tasks where they are, then they get a chance to see how other students have thought about the tasks, and then they begin to learn from each other.
And so types of multiple entry level tasks include open-ended tasks that have many avenues of access and allow students to respond in a variety of ways. They include tasks that require students to explain answers, solve non-routine problems, make conjectures, justify their answers, and make predictions. And then open middle tasks require one correct answer, however, students may provide different paths to that answer, and that’s what makes it really nice, is that students can see that there are multiple ways to come to a solution.
And then we want to make sure that we’re using worthwhile tasks. And so worthwhile tasks, regardless of the context, worthwhile tasks should be intriguing, with a level of challenge that invites speculation and hard work. These tasks often can be approached in more than one way, such as using an arithmetic counting approach, drawing a geometric diagram, enumerating possibilities, or using algebraic equations, which makes the task accessible to students with very prior knowledge and experience.
Jon Orr:
Next up, we have Dr. Ayanna Perry talking all about learning goals, how to create them, and the importance of those learning goals. Here we go.
Ayanna Perry:
Okay. And so, want to talk a little bit about their learning goals as equitable teaching tools. Again, from our text, equitable teaching for us is the pedagogy and practices we use to ensure every student has access to high-quality, on grade level curriculum and instruction in a learning community that values their contributions. And I would add that those contributions are mathematically-pertinent, right? You know, I really love math and I like being in math classes, but I didn’t want to be the kid they were like, “I just really love it that you’re so eager to learn.” For me, that’s great. I like being an eager learner, but I also want to know that the questions I ask help move the work forward, because I’m helping myself and my classmates dig deeper into the mathematics that we’re understanding.
This is similar and related to an idea of assigning competence that comes out of a complex instruction pedagogy out of California, but the idea here is that the contributions that we value about all students should be mathematically relevant. And every student is making a contribution that is mathematically relevant when they’re engaged in the work, and as teachers, the more we name that, the more we develop confidence in our students about their ability to engage in work, right?
So learning goals as a tool for equity. Your detailed learning goal should broaden our perspective of doing math. And in our examples, we’ve looked at use the operation of addition using manipulatives, using the fact family, explaining what solutions mean in words, right? Like those are all the ways in a class that I would look for someone engaging in math. In our assessment of who is doing math, if I’m only looking for using the appropriate operation, one type of thinker, and the person who probably most quickly gets to the solution, is who gets to be doing math. But if I’m looking for all these different ways and also connections between those different ways, then more students are on my radar.
It also broadens our understanding of students’ capabilities. Sometimes, “I can’t,” just means, “I need another strategy, I need another structure, I need something else to kind of help me gain access.” I’m reminded of Lesh. I don’t know his first name. But there’s a Lesh model to tasks, and it’s, usually, books start with words or pictures, but there’s also, you could start with a model, you could start with a written word, you could start with a symbolic measure.
And so sometimes, what I notice in my own practice is there is a form of math problem that I like the most that makes it easier for me to engage in the problem, and that’s the one I just give to my students all the time. And so if I switched up how I invite students to engage in the work, then I can’t shift to, “Oh, I know how to get into this. I can make sense of this picture. I can make sense of these symbols.” So making sure that we vary the way that we introduce math so that we are also inviting students to show us what they know. And then it also supports students in building confidence in their capabilities. Once we are giving them more time to show what they know, we are also able to point it out for them.
So what are learning goals not? They should not be vague statements of what students will know by the end of a lesson, and we actually don’t share this form of the learning goal with our students. They aren’t narrow statements of what doing math is, that only shows one way of competence, and they are not for some students and not others. This is a really hard one. You know, I can dream about all the things I want to do in a lesson, but if in my dreaming, I’m not considering all of my students and I’m not thinking about ways that everybody can get into the lesson, then I’ve got to think a little bit harder about what it means to do math in my class for all of the students that I am invited to teach and care for, right? And so really want to be thinking about when we’re doing our learning goals, how we’re including everyone and what learning goals are. So they are detailed, measurable statements of what students will learn, demonstrate, and do by the end of a lesson, and they’re to be shared with students in a different form.
So this is a form of a learning goal I might share with the student. “Today, you’ll expand your application of simple operations to solve for X. You’ll also continue to discuss equivalence to differentiate it from equality.” Students know what they need to be thinking about and they know what conversations they’re going to continue, and it’s to be applied to all students.
Kyle Pearce:
All right. Next up on our list is Isis Spann, and guess what, Isis is passionate about kindergarten math, and hey, who shouldn’t be, right? Kindergarten math is the foundations, the building blocks of helping our students become numerically fluent and flexible. So take it away here, Isis.
Isis Spann:
Just some quick data points from my data people that love data. I wanted to make sure that you guys felt welcome during this talk. So I brought you in some numbers from South Carolina, specifically, around mathematics and our kindergartners that are coming into the classroom. 50% of our kindergartners are entering the classroom unprepared to do reading, basic foundational reading and basic foundational math. We are in the era where math is almost like second to reading, where everyone’s in love with reading and they’re reading logs, reading conferences, and reading trophies, and math sometimes gets that Cinderella-in-the-beginning-of-the-movie treatment, where everybody hated Cinderella, and the stepsisters were evil, and all of those different things, and then by the end, which this era that we’re in right now, everyone is just like, “Oh, you know what? Math is important, too.”
So this is why spaces like this is very important. Presenters, administrators, teachers like ourselves are very important because we have to continue to carry the torch for math. We have to continue to speak up, we have to continue to advocate for it, because data is showing that our children are showing up and they’re not prepared. There are jobs being created for children that need this really strong foundation in math and they’re going to be ill-prepared, and as early childhood educators, it’s really on us to build that foundation early, build that love of math early so that they can continue to build on that as they go through the remaining grades that they will go through.
All right. So one of my favorite math mentors came up with the term mather. She says that readers read, writers write, and mathers math. And what we do at FUNdamentals of Learning, before we start any tutoring session, before we start any workshop, we always put this affirmation out that, “I am a mather. I can read numbers, I can write numbers. I am a great mathematician.”
As an educator, this is the biggest piece for me because a lot of children that I encounter, they are not confident, right? Before we can even get to content, before I can even get to teach them, they already feel defeated. And just like the mom in this photo, every family that I work with, they always get affirmation cards because even families need to know that you can do this. It might look different, it might sound different, it might not be what you experienced when you were a kindergartner or when you were going through school, but we’re in this together. So this affirmation really helps us to build that family, it helps us to build that connection so that families understand that they can do this role just like the educators and the teachers in the building can do that role as well.
Jon Orr:
And you’re in for another special treat here. Dr. Nicki Newton is back. She’s been with us a number of times in the summit and also on this podcast. She’s going to share some info and some practical lessons about counting and why counting is just more than 1, 2, 3, and we want you to capitalize on her insight. So here we go.
Dr. Nicki Newton:
So today, I want to talk about Clements and Sarama learning trajectories, and there’s around 20 in the Number Worlds book. They had around 20 levels, and they’ve played with that a little bit on the Learning Trajectories site, but basically, they’re the same. My question always is, why is everybody working on the number four when I go into the classroom? Because they’re like, some kids know the number four, other kids are still trying to figure out what one looks like, some kids are like, “I know what a thousand is.” So why is everybody working on the number four? Why is it that we teach counting in such a regimented way that, “Today is the number four, and if you don’t know any of the other numbers, oh well, and if you do, oh well, because today is the number four and tomorrow’s the number five, so you better get the number four today”?
But what happens if you missed three? I don’t know. So my question is, why do we teach counting in that lockstep way? I really believe what Tomlinson said. At its most basic level, differentiating the instruction means shaking up what goes on in the classroom so that students have multiple options for taking in information, making sense of ideas, and expressing what they learn. In other words, a differentiated classroom, avenues to acquiring content, to processing or making sense of ideas, and to developing products so that each student can learn effectively.
We know that play is important. In 1959, the UN Declaration of the Rights of the Child said that play is actually a right of the child. And in 1977, the International Play Association had written extensively about play and its importance in the role of learning, as well as [inaudible 00:19:50]. So play, how do we do it? Why do we do it? How is it important? In classrooms, still often I will see things like this, worksheets. But see, it’s not play or learning. It’s both. And I think bingo, for example, is a great example of that. You are playing, but you are learning. So instead of just drowning our kids with worksheets, we should do stuff like this. Games are a great playful way to get children to engage in powerful mathematical thinking, right? Powerful mathematical thinking.
So is it just this or is it that, right? So this is my friend Nancy Numbers, right? Or you can call him Neil the Number Cruncher. And he’s right here, and what Neil does is he eats numbers. So again, it’s a form of play, but I’m asking kids to do something that is academically-based and standards-based to recognize numbers. So the kids might all have numbers and then I’ll say a number. They have to recognize their number and feed Neil. So the point is that play should be an active part of what we do every day. So I want to set that as kind of our theoretical framework, play as a basis of understanding, as a foundation for learning to do things.
So looking at the 20 levels, and I told you I’m building on mainly Clements and Sarama, but certainly, I’m building also on the work of Wright and Bermejo out of Spain. I mean, there’s so many people that have done excellent work around counting. But when Clements and Sarama talk about learning trajectories, there’s a counting trajectory in particular. They have tons of trajectories, but they have a counting trajectory in particular. And they talk about learning trajectories as the standard or goal, then the developmental learning trajectory, and then the activities for the learning trajectory. And oftentimes, what I see in classrooms is teachers going, “What’s the standard? What’s the activity?” rather than, “What’s the standard? And then what is the learning trajectory of that standard?” and then based on that learning trajectory, where students are, we’re going to give them appropriate activities.
Kyle Pearce:
All right. Next up, we have a clip from a recent podcast episode, where we spoke with Pamela Seda. Pamela is the co-author of Choosing to See: A Framework for Equity in the Math Classroom, and you’ve got to listen to this entire episode after you hear this clip. But here’s a little snippet and a big takeaway for you.
Pamela Seda:
So one of the things I’ve realized that my goal as a teacher is to uncover the brilliance in every kid. There’s some brilliance there. There’s something that they contribute, there’s some knowledge, and that’s my job, is to figure out how to contribute, how to help them contribute to the conversation, including my own knowledge. So every time that I taught a class, I always learned more about whatever it was that we were learning about.
Kyle Pearce:
I love it, I love it.
Pamela Seda:
I just think that helping students develop competence and confidence is the, I guess, result, the end product of helping kids understand that, “I have something to contribute to the knowledge of the group,” and that, “We’re learning as a community, not just as an individual.” I don’t know about your students, but my students would think, “I’m just supposed to look at the problem and it’s supposed to automatically make sense to me,” not understanding that oftentimes, there’s something you need to do. You might need to draw a picture, you might need to try some things, you might need… Usually, there is some process that you have to go through, some effort to even make sense of the problem, and I think that’s important to communicate to kids because if you don’t, some kids will mistakenly think, “Well, I looked at this problem, it doesn’t make sense to me, so I must be dumb. I must not be a math person.”
Even if students did things that I didn’t want them to do, they may have been disruptive in class, and that didn’t mean that I don’t hold them accountable, but I realized that I can always do it in a kind way, that being mean or harsh is never called for, that you do demand, I have had high expectations, but that warmth and that communicating to students and actually saying, as research says, when you follow whatever your instruction is with, “I have high expectations of you, but I know that you can meet them.” When you communicate that to students, it really is a motivator, and research says that that works, especially for students who have been marginalized. So that’s one thing that comes to mind, being that warm demander.
Jon Orr:
And our last speaker is Tashana Howse. And you’re going to hear a clip from a recent episode from the podcast that we spoke with Tashana, and you’re going to learn all about how to make equitable support for our students in the math classroom.
Tashana Howse:
Knowing your students and then having a keen understanding of the content, and that understanding have to be in a way that we understand the coherence of what comes before me and after me, meaning, what I’m teaching, if I’m teaching algebra, what happens in middle school that connects or bridges that algebra, what happens in the Algebra 2 geometry. So having those two things together are going to help us unpack really good equitable assessments for our students.
Jon Orr:
Yeah, totally, like knowing what they can do and knowing the student is so important. And unfortunately, I think, for a lot of teachers, and I’m going to go out on a limb here, because Kyle and I always kind of pash on high school teachers because we’re both high school teachers by training, I’m still a high school teacher, but high school teachers, we’ve said in the past like I think a lot of elementary teachers get into teaching because they really love the kids, and it’s very natural for an elementary teacher to go like, “I want to teach the kid. I got to get to know the kids,” whereas I think high school teachers, especially for me, and I guess that’s why I’m speaking from experience, I had to learn that. Because a lot of us get into teaching because we like the subject. We liked mathematics, we had an affiliation with it. We like fell in love with mathematics and then we’re like, “I want to pass that on to kids.”
So when I first started teaching, it was that love of mathematics. I tried to share that love by being really excited about mathematics, but I still, I think, was solely focused on the mathematics and the lessons and not the actual students, and I think a lot of teachers are still in that place. So I’m wondering, Tashana, if you could fill in some gaps for those people? I know that most listeners of our podcast are probably teachers who already know that they have to teach kids and have to understand and get to know students, but I’m wondering if you can compare and contrast? Like think about a teacher who is only focused on the mathematics and not the student and what they’re missing out on for assessment, for helping that student along, versus a teacher who is solely focused on helping that student and getting to know that student. I wonder if you could paint us a picture of like what this teacher’s missing out on, like my old self, what was I missing out on, versus having a teacher who, what you’re saying, should be doing for these equitable teaching practices?
Tashana Howse:
Awesome. So Jon, that was great. I’m going to answer that question. So just to answer your question, so what are some teachers missing out on? Number one, it’s like you missed the opportunity to really connect the content with the learner. Because when we think about it, and Jon, you said it well, is that we were math teachers because we are just really good at the numbers. We love the math. We just understand all that stuff and we get excited about it. But there are so many kids that are not just naturally excited like we are. Like there are kids that they’re going to look at you and just be like, “Okay, what’s the point? Why? Why am I learning this?” And so if we’re not connecting them to it, then we’re missing that moment, we’re missing that opportunity to be able to connect them back to the learner.
And I’ll say, when I was a freshman and I was in an algebra class, I learned a lot of… I mean, I’m really good with the numbers because we are good naturally, as math teachers. It’s like I was going through the motions, just doing a set of procedures, a set of problems, and I felt sorry for the kid. I got it, like it was easy for me because I was in a regular math class. It wasn’t advanced. It was regular. So you got this really bright gifted math girl in a math class, but all of the people that were in that class, they were like one or two grades ahead of me. I’m like the only freshman. And I got it, I understand it all.
So I’m saying all that to say is that these kids were just learning a bunch of procedures, and there was no connections, no anything, and there was like behavior problems in the class. So this little shy little Black girl who was really good at everything, I just kind of stayed in my desk and I just was in my little space until I reached that geometry class where this teacher connected it all, like we were building cities with the content. So we discovered all this geometry and then we began to build cities. So think about what will you need in your city for your city to operate. So then you start to think about all these different components. So that’s what you miss out on. You miss out on the opportunity to connect the content that you are so excited about with the learners that are sitting in front of you. When you connect those things, then that’s when we can provide equitable teaching practices and equitable assessments for kids.
Kyle Pearce:
Well, Jon, as always, we are always learning in the Making Math Moments That Matter community, but wow, it’s great to re-listen to some of these key points. And it’s interesting because although we’re there running those summit sessions live and interviewing people on the podcast, as you heard with our last few speakers, there’s always something new to take or glean from these amazing, amazing speakers. So friends, something that’s really fantastic is that if you head to our show notes page over on episode 221 over on makemathmoments.com/episode221, not only do we have the links directly to the podcast episodes that we just had clips from, but all the other speakers who were in our 2022 Virtual Summit and all of those are hosted inside the Academy. Now, while you can grab 30 days in the Academy 100% free, we’ve actually opened those particular sessions so they are easily accessible by anyone without even having that Academy membership. So go gobble them up over at makemathmoments.com/episode221 so you can dig deeper with these key messages from these fantastic speakers.
Jon Orr:
Thanks for sharing that, Kyle. And hey, as always, folks, what have you pulled from these episodes? What’s resonating with you currently? How are you going to hold yourself accountable? Are you going to share this with a colleague, someone at the lunch table? Have a discussion about some of the big takeaways here for you. You can always do that also over in our free private Facebook group, Math Moment Makers K-12, hit us up on any social media, ask questions, and reach out to us at Make Math Moments over there.
Kyle Pearce:
Love it. Well, my friends, until next time. I’m Kyle Pearce.
Jon Orr:
And I’m Jon Orr.
Kyle Pearce:
High fives for us
Jon Orr:
And a high five for you.
DOWNLOAD THE MAKE MATH MOMENTS FROM A DISTANCE CHEAT SHEETS
Download the Cheat Sheets in PDF form so you can effectively run problem based lessons from a distance!
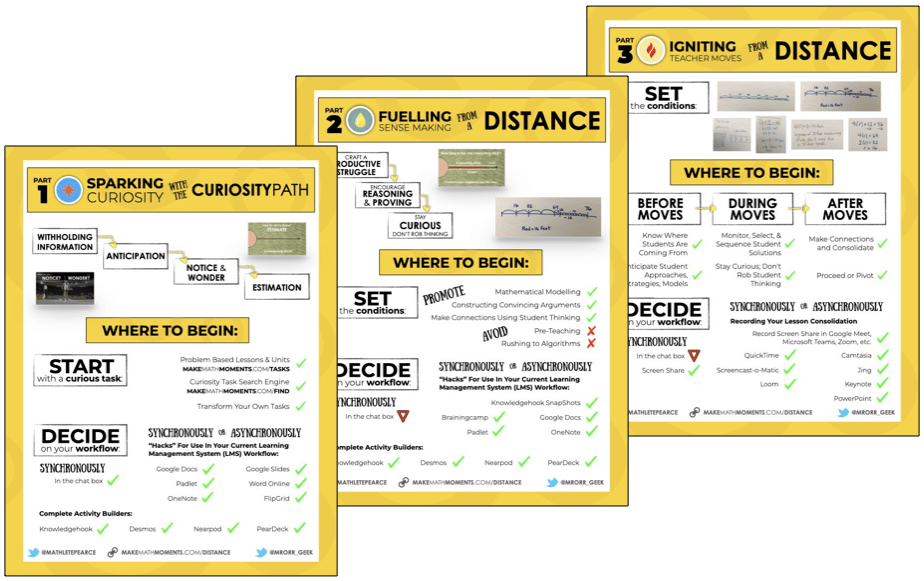
UP YOUR DISTANCE LEARNING GAME IN THE ACADEMY
There is a LOT to know, understand, and do to Make Math Moments From a Distance.
That’s why so many Math Moment Makers like YOU have joined the Academy for a month ON US!
You heard right: 30 days on us and you can cancel anytime. Dive into our distance learning course now…
Thanks For Listening
- Apply for a Math Mentoring Moment
- Leave a note in the comment section below.
- Share this show on Twitter, or Facebook.
- Leave an honest review on iTunes. Your ratings and reviews really help and we read each one.
- Subscribe on iTunes, Google Play, and Spotify.
ONLINE WORKSHOP REGISTRATION
Pedagogically aligned for teachers of K through Grade 12 with content specific examples from Grades 3 through Grade 10.
In our self-paced, 12-week Online Workshop, you'll learn how to craft new and transform your current lessons to Spark Curiosity, Fuel Sense Making, and Ignite Your Teacher Moves to promote resilient problem solvers.


0 Comments