Episode #371: Three (3) Critical Math Topics To Avoid Rushing To The Algorithm
LISTEN NOW HERE…
WATCH NOW…
In the push to cover content and keep pace, it’s easy to jump straight to the algorithm. But what if that focus on efficiency is doing more harm than good? In this episode, we explore how rushing to procedures can rob students of opportunities to reason, make connections, and develop true mathematical understanding in three(3) critical math topics. Together, we’ll unpack what’s really at stake—and how a shift in mindset can help you cultivate curious, confident math thinkers. Slowing down might just be the most powerful move you make.
Key Takeaways:
- Why students fall back on tricks—and what to do instead.
- The impact of jumping to algorithms too soon.
- How to create space for reasoning and connection.
- Practical strategies for building conceptual understanding.
- Shifting your math block from procedural to purposeful.
Attention District Math Leaders:
Not sure what matters most when designing math improvement plans? Take this assessment and get a free customized report: https://makemathmoments.com/grow/
Ready to design your math improvement plan with guidance, support and using structure? Learn how to follow our 4 stage process. https://growyourmathprogram.com
Looking to supplement your curriculum with problem based lessons and units? Make Math Moments Problem Based Lessons & Units
Be Our Next Podcast Guest!
Join as an Interview Guest or on a Mentoring Moment Call

Apply to be a Featured Interview Guest
Book a Mentoring Moment Coaching Call
Are You an Official Math Moment Maker?

FULL TRANSCRIPT
Yvette Lehman:
We’re going to dive into probably one of my favorite topics. I think I say that a lot on this podcast. They’re always my favorite. I know. But as you all know, I obviously am a huge fan of building procedural fluency from conceptual understanding because starting with procedural fluency just never worked for me as a learner. And so this has been the bulk of the work that I’ve done as an educator. And I know you’ve both been on this journey as well.
Jon Orr:
I think you do. was going to say, how can every topic be your favorite topic?
Kyle Pearce:
Yeah. It’s all lies.
Yvette Lehman:
So today we’re gonna highlight, it’s almost like a top three reel, know? our, almost like a top 10, but top three concepts where rushing to the algorithm can do a significant amount of harm or let’s say undermine a significant amount of thinking.
Kyle Pearce:
Hmm
Jon Orr:
We’re all bringing one example. So it’s like top three, but it’s really like our top one for each of us.
Kyle Pearce:
Ooh, yeah, it’s like three tops like the one I’m gonna be selfish and I’m gonna go first because I’m worried. I’m worried john might steal this one from me. But I know we’ve that’s not going to because I know what she’s gonna say. But for me, I’m picturing the law or no, no, I was gonna say long division, actually multiplying multiple digit numbers because and here’s my big my big why is because it has
Jon Orr:
you just want to get it out there.
Kyle Pearce:
so many opportunities if we do this conceptually from the start in order to stretch all the way into algebra and to be able to do things that are traditionally very difficult like completing the square, which, know, way, way up into high school. It’s like if we start, yeah, if we start all the way back in elementary school and we are doing actual multi-digit multiplication and we’re utilizing
Jon Orr:
My favorite.
Kyle Pearce:
you know, arrays and we’re utilizing the open array and we’re drawing this out, you can very, very easily make connections all the way through as we start multiplying by different digits, by actually throwing in some algebra in there and getting into some pretty complex situations such as the quadratic type work that we do in some of our
you know, grade eight all the way to grade 10 classrooms, depending on which part of North America you are learning in.
Jon Orr:
Now I’m going to, I’m not going to piggyback on this, but so, but I do want to comment on this because I had thoughts around this and to extend, you know, the why here behind this particular say rush to the algorithm. And I think, and I think it’s a cautionary tale as well in a sense of like, cause I think we rushed for a long time as teachers rushed to teach kids how to multiply at the high school level or the distributor property. And you, you will hear teachers still use foil.
you know, and use the four letter word that starts with F to help kids, you know, multiply a binomial by times a binomial. And really what you’re doing is like you’re saying, Kyle, you’re multiplying two-digit numbers by two-digit numbers and we can replicate that in different ways to make kids the connections vertically across grade levels. where my say spin off here, now this isn’t gonna be my thing. I’m gonna let Yvette go first after I make a comment here.
Kyle Pearce:
Right.
Jon Orr:
But what I wanted to comment, it says not to, because this is yours. This is yours. This is yours. So what I want to comment here on though is to be aware of the conceptual part and trying to make sure that we build on the conceptual. Like you’re saying, Kyle, because I think I still see or hear a lot of like I’m using the box method or I’m drawing a box and I’m multiplying. I’m multiplying here.
Kyle Pearce:
Window method.
Jon Orr:
by filling in the boxes. And that’s the concept. I’m doing conceptually because I’m using this box diagram. But I think where the cautionary tale here is, is to make sure that we continually reflect on why that box method actually is working if you’re calling it the box method. Because if you’re not, say, referring to, say, how it’s developed from arrays into the area model to continue up the ladder,
so that when you do get to algebra and you’re drawing a box method or a diamond method or whatever you want to call it, the worry is that you’re really just replacing one algorithm for another. Because you couldn’t show kids the box method and they might say, hey, I’m teaching conceptually, but all kids are doing is memorizing that algorithm that you just showed them instead of the standard algorithm or the foil method if you wanted to live in algebra land for a minute because
That’s my concern about say this and rushing to the algorithm is consider what algorithm you’re teaching and what is the progression to learn the algorithm and why that algorithm works. So rewind and go, let’s go back to why area matters here and teach it through say area instead of just replace one algorithm with the other. So that was like my little caveat on your top rush.
Kyle Pearce:
Well, you know what, I’m glad you shared it because I wasn’t thinking about that, but it is so common, right, where we see people proceduralizing the use of, a model instead of actually utilizing the model as sort of a window to get you closer from like the, you know, and I’m going to say more, you know, say the more concrete to the more abstract, right? And you’re really trying to connect. But if we lose track,
Right. If you lose track of what it was connecting to and what you’re trying to get yourself towards, then it’s all for not. Right. So I think that’s a great reminder that you’re giving folks is to go, you know, it’s more about gradually pushing along this trajectory. Right. And, you know, we talk a lot about fly wheels. It’s like in math understanding, it’s like a flywheel. shouldn’t be abandoning the original conceptual piece. We should be coming back.
every so often so that we don’t lose sight. Like we don’t forget about why it is that we’re doing what we’re doing because as humans are our minds are programmed to save having to think, you know, that that it takes energy, it takes calories in order to be thinking deeply. we need to really be promoting that so that we don’t lose track of it. So I think it’s a great one. Yvette, I want to hear yours. I I’m gonna
Yvette Lehman:
Everybody’s going to assume that I’m going to do long division because I feel very passionately about division, but we have an entire episode dedicated to that context. So if you want to check that one out, think it’s, I don’t even know somewhere in the hundreds. I did an episode around division through the years. Okay. So here, this is what I’m going to say. I chose fraction as operator.
Jon Orr:
Ooh, that’s not even what I thought you were gonna.
Yvette Lehman:
but not just fraction, I’m gonna include fraction decimal percent as operator. Okay, my issue with this concept is I think it’s introduced way too late and when it is introduced, it’s proceduralized. So kids are like punching decimals into calculators and multiplying it by a whole number. I think we should be introducing this concept with benchmark fractions as early as primary. Like where we’re describing
half of something, a fourth of something, a sixth of something, a tenth of something. Like I think that spatially, if students can understand magnitude and then partition, which is connected to part of division, even if it’s through estimation and reasonableness only, you know, I think that’s about a fourth of the total group. I think that’s about 25 % of the total cost. I think that
relative reasoning, which we talked about Kyle in another episode, is a critical, critical skill for students that we don’t introduce early enough and then when we do, we make it almost blind where they’re not actually looking at the relative size of quantities.
Kyle Pearce:
I have two things to say about that. One is, the first is, I should have known because the most recent webinar that we had done was on that topic. And I know, and you and I are very similar in that when we’re planning a webinar, the topic is usually the one that’s top of mind for us. So I should have known that. I know you well enough. But no, the second piece and I think the more important part is just seeing how, like not only how important it is, but how
easy it could be in order to do this routinely, like in order for us to be asking children, whether it’s your own children or students in your classroom, to make these sorts of estimates, it doesn’t have to be perfect, but estimating when they’re looking at a submarine sandwich, you know, about how much is one third of that sandwich or
talking about percentages and you know, asking them when they’re in the gym doing an assembly and saying, you know, if there’s a hundred kids here about, you know, how much would it be to have 28 % of those hundred and extending from there. These are, these are moves that if we’re intentional enough about them, we can make such a significant difference.
in how students approach this, what is often a very, very foggy and scary sort of content area for students, fractions, decimals, percents. And yeah, I really like it. It was a sneak move by you, but again, I should have known better.
Yvette Lehman:
John, what’s your top? Let’s hear it.
Jon Orr:
Okay, well guess mine is somewhat related to yours because I think mine is teaching kids cross multiplication of cell proportions. think in hindsight, because I used to do this when I first started teaching kids, and this is, you algorithms come from, if I want to show kids something, I’m just going to show them the fastest way to do it, but not always the most efficient. And this comes at, say, an expense that we don’t need.
we don’t need to like have. Because I don’t think anymore that there’s a reason to do any cross multiplication to solve, these types of problems, especially when there’s so much richness. When, say, we can represent that proportional statement on a number line or a double number line and use that model and the strategies along that model or using that model to scale in tandem, know, forwards, backwards, use unit rates, like
Like there is so much written is to solve every proportional problem out there that would require cross multiplication in a way that allows way more like so much more thinking around what that proportional statement means. And it can solve so many problems around helping kids solve proportional statements. Because you’re helping them understand that, hey, if I scale this down or scale this up, I’m working within ratios, I’m working with rates. I’m like, there’s just so much there that
it’s it’s a disservice if we’re just jumping to that algorithm and showing kids because, you know, again, just drawing that double number line and scaling or even if you want to use a ratio table, it’s better than say, multiply this because teachers who who are also on our side with with cross multiplication are also going kids are trying to use it to solve, you know,
other problems that don’t even make sense. They’re just seeing two fractions beside each other and they’re like, I’m just gonna cross multiply. I’m like, no, this is not the case. You use cross multiplication. My own daughter did it the other day. She’s like, I’m just, she saw these two fractions sitting beside each other. I’m just gonna cross multiply. No, let’s talk about what we’re really doing here. So that’s mine and I will die on a hill.
Kyle Pearce:
Hmm. You know what I now that you said, I’m like, I should have known, you know, like, I know, like you spent so much time and I know, I know, you know, I’m disappointed in myself, you know, is what it is. But, you know, I want to make an explicit point here because John, said yours was similar to events and some people might be listening and maybe not recognizing how similar they really are in the fact that when we are using
percent or decimal or fraction as operator that utilizing a double number line can be a really helpful tool and essentially setting up a proportional relationship. So the reality is even though Yvette wasn’t talking about cross multiplying specifically, she was talking about, let’s say, punching numbers into the calculator, which I think we’ve all done it. You know, we’ve been guilty of it. I’ve taught it, you know, so again, this is no judgment here. It’s about how do we get a little bit better and
The part that I think is so interesting is the fact that if what Yvette is saying is true, which I believe it to be, that we can get students doing this at very early ages, making early estimates, utilizing percent decimal fraction as operator, then essentially what we’re saying is that students can solve proportional relationships when they are very young. And yet I’m sure there are many listening right now who are saying there are students in my blank
grade classroom that are unable to do so. Maybe it’s grade seven, maybe it’s grade nine. In our cases, John, we’ve seen it where you have students in grade 10, 11, even in grade 12, where they’re getting lost in the procedures and they have essentially trained themselves or learned that they don’t need to actually think they’re just going to follow the steps. And that is holding them back when we’re saying that actually all students
are able to access this content. Now, maybe different values might need to change and different contexts might need to change, but this is definitely a lot of the work. And I think some of the maybe easiest content work that we can focus on because they have legs, right? All the examples we’ve talked about, they have that long legs that you can go and you can do this at early ages all the way through and you can all rally together.
in buildings and districts to work on this type of math content knowledge together.
Jon Orr:
For sure. And just on your example there, it’s like, it’s not even too late for the high school or the students that you’re saying at blank level, they don’t know how to solve for this yet. But it’s like, that’s the time to now bring it in. Even though it might take you a little extra time, it’s 100 % worth it. See what I did there? 100 % worth it. Today we talked specifically when we think about our tree, know, our classroom trees, our program trees at the school level or at the district level.
the six components that make up effective classrooms or programs. I think we highlighted and touched strongly here on two things, one being the roots of the tree, understanding the math behind the algorithms, and the conceptual understanding is essential for us to be able to give our students these experiences. So strengthening our own roots of the tree is
how we strengthen our classroom experience for our students. One of the ways that we’re trying to do that for you other than say this podcast, which is a glimpse of practices that we could be putting into place or understandings that we could be putting into place. We are holding monthly trainings like we mentioned here, monthly say webinars where we unpack say the mathematics in a maybe misunderstood topic or like this one, a rush to the algorithm type topic where we’re going to unpack the math.
while we unpack a lesson or a task or a unit that you could then use with your students. So you can head on over to makemathmoments.com for training and see what say current webinar we have while we’re holding them every single month. The other part is I said the roots but also say the branches of our tree which is our pedagogical moves. We have to strengthen the roots so that we can have strong branches.
We talked about that here about making choices about what models and strategies to use with our students. If you want to learn more about the tree, head on over to makemathmoments.com forward slash report. We’ll send you a little info about how your tree is growing. Again, that’s makemathmoments.com forward slash report.
Thanks For Listening
- Book a Math Mentoring Moment
- Apply to be a Featured Interview Guest
- Leave a note in the comment section below.
- Share this show on Twitter, or Facebook.
To help out the show:
- Leave an honest review on iTunes. Your ratings and reviews really help and we read each one.
- Subscribe on iTunes, Google Play, and Spotify.
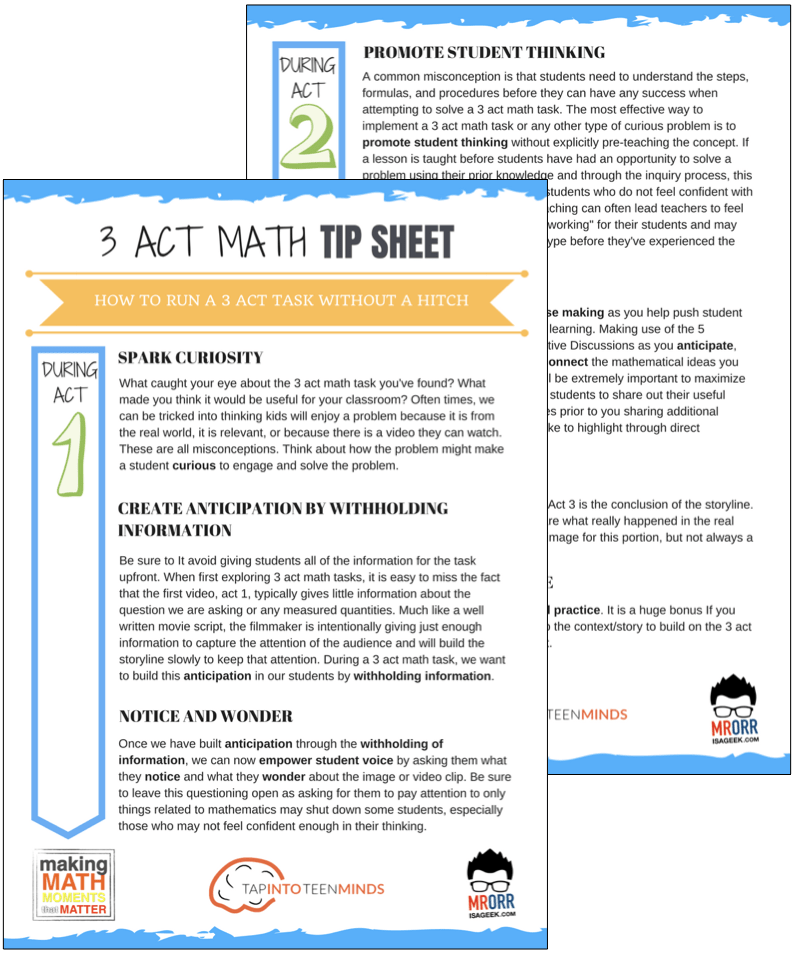
DOWNLOAD THE 3 ACT MATH TASK TIP SHEET SO THEY RUN WITHOUT A HITCH!
Download the 2-page printable 3 Act Math Tip Sheet to ensure that you have the best start to your journey using 3 Act math Tasks to spark curiosity and fuel sense making in your math classroom!
LESSONS TO MAKE MATH MOMENTS
Each lesson consists of:
Each Make Math Moments Problem Based Lesson consists of a Teacher Guide to lead you step-by-step through the planning process to ensure your lesson runs without a hitch!
Each Teacher Guide consists of:
- Intentionality of the lesson;
- A step-by-step walk through of each phase of the lesson;
- Visuals, animations, and videos unpacking big ideas, strategies, and models we intend to emerge during the lesson;
- Sample student approaches to assist in anticipating what your students might do;
- Resources and downloads including Keynote, Powerpoint, Media Files, and Teacher Guide printable PDF; and,
- Much more!
Each Make Math Moments Problem Based Lesson begins with a story, visual, video, or other method to Spark Curiosity through context.
Students will often Notice and Wonder before making an estimate to draw them in and invest in the problem.
After student voice has been heard and acknowledged, we will set students off on a Productive Struggle via a prompt related to the Spark context.
These prompts are given each lesson with the following conditions:
- No calculators are to be used; and,
- Students are to focus on how they can convince their math community that their solution is valid.
Students are left to engage in a productive struggle as the facilitator circulates to observe and engage in conversation as a means of assessing formatively.
The facilitator is instructed through the Teacher Guide on what specific strategies and models could be used to make connections and consolidate the learning from the lesson.
Often times, animations and walk through videos are provided in the Teacher Guide to assist with planning and delivering the consolidation.
A review image, video, or animation is provided as a conclusion to the task from the lesson.
While this might feel like a natural ending to the context students have been exploring, it is just the beginning as we look to leverage this context via extensions and additional lessons to dig deeper.
At the end of each lesson, consolidation prompts and/or extensions are crafted for students to purposefully practice and demonstrate their current understanding.
Facilitators are encouraged to collect these consolidation prompts as a means to engage in the assessment process and inform next moves for instruction.
In multi-day units of study, Math Talks are crafted to help build on the thinking from the previous day and build towards the next step in the developmental progression of the concept(s) we are exploring.
Each Math Talk is constructed as a string of related problems that build with intentionality to emerge specific big ideas, strategies, and mathematical models.
Make Math Moments Problem Based Lessons and Day 1 Teacher Guides are openly available for you to leverage and use with your students without becoming a Make Math Moments Academy Member.
Use our OPEN ACCESS multi-day problem based units!
Make Math Moments Problem Based Lessons and Day 1 Teacher Guides are openly available for you to leverage and use with your students without becoming a Make Math Moments Academy Member.
Partitive Division Resulting in a Fraction
Equivalence and Algebraic Substitution
Represent Categorical Data & Explore Mean
Downloadable resources including blackline masters, handouts, printable Tips Sheets, slide shows, and media files do require a Make Math Moments Academy Membership.
ONLINE WORKSHOP REGISTRATION

Pedagogically aligned for teachers of K through Grade 12 with content specific examples from Grades 3 through Grade 10.
In our self-paced, 12-week Online Workshop, you'll learn how to craft new and transform your current lessons to Spark Curiosity, Fuel Sense Making, and Ignite Your Teacher Moves to promote resilient problem solvers.










0 Comments