Episode #414: How to Sequence Math Tasks: Thin Slicing in BTC (Building Thinking Classrooms) Explained by Peter Liljedahl and Kyle Webb
LISTEN NOW HERE…
WATCH NOW…
How do you move your students from confusion to confidence—one question at a time when Building Thinking Classrooms?
If you’ve ever found yourself wondering how to keep every student engaged without oversimplifying your math lessons or overwhelming your class with complexity, you’re not alone. Many math teachers face the challenge of designing lessons that meet all learners where they are—without sacrificing depth or progress. In this episode, Peter Liljedahl and Kyle Webb unpack thin slicing, a powerful strategy that helps you guide students through content with just the right level of challenge at every step. Whether you’re just starting with Building Thinking Classrooms or deep into the journey, this conversation clarifies what thin slicing really is—and what it’s definitely not.
Listen now to discover:
- Why thin slicing isn’t just another way to sequence tasks—it’s a mindset shift for responsive, dynamic instruction
- The practical do’s and don’ts that make or break thin slicing in your classroom
- How to start building your own thin-sliced lessons using tasks you already have
Press play to demystify Building Thinking Classrooms’ thin slicing and learn how to keep your students thinking, engaged, and moving forward—one purposeful task at a time.
Attention District Math Leaders:
Not sure what matters most when designing math improvement plans? Take this assessment and get a free customized report: https://makemathmoments.com/grow/
Ready to design your math improvement plan with guidance, support and using structure? Learn how to follow our 4 stage process. https://growyourmathprogram.com
Looking to supplement your curriculum with problem based lessons and units? Make Math Moments Problem Based Lessons & Units
Be Our Next Podcast Guest!
Join as an Interview Guest or on a Mentoring Moment Call

Apply to be a Featured Interview Guest
Book a Mentoring Moment Coaching Call
Are You an Official Math Moment Maker?
FULL TRANSCRIPT
Jon Orr: All right, we’re gonna dig into thin slicing today. And I’m excited to dig into thin slicing, because it’s topic that I think we need to talk about. And I think, I’ve got the two guys here that are ready to talk about. Peter’s here, Kyle’s here. Let’s get into it, guys. The only question before we launch and before we get our in-depth talk going on here is the only question we have asked every single guest, and this is gonna be episode 414 and and Peter you were on I just looked this up because I was like when was Peter first on he’s you were one of our first guests you were episode 21 which was in 20 like April of 2019 so that was that was a while ago it was a while ago but the question we always ask if you’ve listened to episodes before is what’s your math moment and so Kyle I’m gonna throw it to you because if you wanted to listen to Peter’s math moment go cue up episode 21 and listen listen over to that one but math moment is like When we say math class, images pop into our minds. These emotions we carry forward from these experiences that we’ve had about math and math class and they shape who we are. Kyle, when I say math class, what’s popping into your mind? Like talk to me about your math moment.
Kyle Webb: There’s a lot. I’m going to share one that I think comes back to why I eventually chose to become a math teacher. And that was back, I don’t know, grade two, three, maybe four, we were doing the famous Mad Minutes. I don’t know if it’s addition, multiplication, I don’t know where we were at that point. The memory’s not that vivid. I remember school went well for me. I was a master mimicker. Peter and I have talked about this many times. Very good at mimicking. I knew how to play the game of school racing through those and getting done and my teacher needing to give me a second one just to like fill the time that we had. And I remember being so proud of myself, so excited. But then I remember my siblings going through the same experience a year or two later, right? I’ve got two younger siblings, a younger sister and younger brother, a younger brother who’s got a disability and their experiences with the exact same interaction was not the same. They had a really tough time where it really affected them and My parents are really good at keeping us in check. I didn’t take this as a moment to think I’m better than them. They, you know, kept us in check and we’re like, well, why is it not so equal for everybody? So we had these really interesting conversations. I remember these from being a child and I think it didn’t really dawn on me until I was in my teacher education program that not everyone experienced math the same way that I did. And in hindsight, you know, my my big goal in math education is to try to equal that playing field, make sure everyone’s having that same opportunity to find the love and joy of math that I found early on. And I think through that, I’ve actually found more passion and love for the subject and the content and the teaching kids math than I may have had otherwise. So that’s what comes to mind for me. There’s many more things I could share, but that one’s, I think, most relevant for our kinds of conversations.
Jon Orr: Sure, sure, yeah. And I echo that. I think we all get to that point where we realize, like when you get into teaching, the way that you internalized the way you thought about this subject or even just understood how learning actually works for yourself is not the same experience for everyone else. I think when you’re a kid, you just don’t get it. Also, I think I still, like you, I don’t think I still got that until after you get into the classroom, you’re seeing a different, kids who are coming from different places and having different experiences, all of a sudden it hits you and you have to decide, how do I wanna handle that? How do I wanna address this different learning style than I have? Because you can go one way or the other way. I went one way for 10 years before I started shifting my instruction. So good on you to recognize super early. Go ahead, Kyle.
Kyle Webb: To be clear, was a lot of adjusting that had to happen once I got started.
Peter Liljedahl: I wonder if this idea that we don’t recognize that others have different learning styles at young ages was a product of the fact that it wasn’t just that time where we doing Mad Minutes, but it’s also that we were operating entirely in isolation. We were in a group as a class, but there was no sort of crosstalk, right? So I think kids have always known that other kids are different, but I was in a classroom today and I was watching kids explain to each other a certain concept and how I’m pretty sure that they understood that the different students in the group had different views of what was going on, could picture the thing differently, needed different explanations. And I think they were seeing that students were learning differently. But in order for that to happen, we gotta, they gotta be in conversation. So I wonder if kids today who spend a lot of time in collaboration solving problems have a different view than we have where we just worked in these silos.
Jon Orr: That’s a good point. I think you, I think you’ve, you know, clearly like identified something for sure. Like I, I never even thought about it like that. It’s like just knowing, you know, just I was sitting in a row just like everybody else and, and you were listening to a lecture and then you had to do your homework. It’s like, you never got to hear a never another thought, an idea, a strategy that wasn’t the teachers.
Peter Liljedahl: First rule of math class is don’t talk about math class.
Jon Orr: Right? And therefore, every—
Kyle Webb: Yeah.
Jon Orr: Yeah, second rule is do your homework. All right, guys, let’s get into thin slicing. You’re both co-presenting at the seventh annual Make Math Moments Virtual Summit this November. You’re running a session for thin slicing, but why thin slicing? We’ve talked about building thinking classrooms, we’ve talked about closing the lessons, we’ve talked about different ways to choose a task in previous sessions, why thin slicing?
Peter Liljedahl: Well, I’ll take the first crack at this and maybe Kyle has a different view. So first of all, you know, like I love talking about this. So it’s why not talk about something that we love talking about. But it’s also, I think thin slicing still has this aura of mystique around it, right? And I think there’s an opportunity here for us to demystify a little bit of this. And certainly Kyle and I spent a lot of time in conversation while we writing the book, but it’s, I think, I personally think that thin slicing is not as hard as people make it out to be. And if we can sort of demystify some of that and just show the pragmatics and the realities of thin slicing through our conversations and through some examples, maybe we can get some traction on that.
Jon Orr: Right. Okay.
Kyle Webb: Yeah, couldn’t agree more. You know, I have this wonderful opportunity to work with so many teachers across all grade levels. And when it comes to that, how do we get through the curriculum question? And we talk, just like use this sin slicing method that we’ve been talking about and building on the thing in classrooms are like, well, how, how do you actually do it? You guys make it look so effortless. And I think part of the reason we want to address this is because it doesn’t have to be the rocket science, right? Teachers know how to do this. They’re looking at those little changes. They’re doing it when they’re Lecturing students, right? We start with a simpler example than the next and we build and we build and build. We can also plan our sequence of how we’re just going to roll out tasks or the questions within a task to our students in a very strategic way. Those little minor variations from step to step to step aren’t as complicated as we think they are. So hopefully we can, like Peter said, demystify this and show teachers that they already have the skill set. They actually probably have resources that have already done a lot of the heavy lifting for them. So lean into that and use it. That’s really what we, I think we hope to communicate across.
Jon Orr: Right, right. Now, if there’s an educator listening who hasn’t, say, taken the deep dive into the work yet that you guys are working on and doing, so maybe just quickly give the snapshot of what is thin slicing, but maybe more importantly, especially for those who have taken the deep dive, is what is it not?
Peter Liljedahl: Okay, so thin slicing is kind of built on two main ideas. So the first one is Mahajic’s Mahaj’s flow, which is this idea that in order to keep students engaged, we need to keep them in that state of balance between the challenge of the task and the complexity, the challenge of the task and their ability, right? And it makes a really nice graph if you think about it, but it’s really about How do I keep them in that perfect balance? Because if the balance is off, right, if the challenge exceeds their ability, they get frustrated. If their ability exceeds the challenge, they get bored. How do we keep them in that balance? Which is, you know, it’s easy enough to think about, but the problem is that the students are doing this thing that we like to call learning. And so as we’re engaging them in this, their ability is increasing. So as their ability increases, we have to also increase the challenge of the task. So that’s part of what thin slicing is. And then the second part comes from Farrance Martin, this idea of variation theory, which is that we notice things that change against a backdrop of things that don’t, right? So we need to have certain things staying the same so that when we change something, the kids will notice that and they’ll pay attention to it. And if that change is big enough to be noticeable, but small enough to not put them into frustration, then we kind of have this perfect balance going. And thin slicing is kind like, how do we do that? How do we take tasks that we already have and put them in a sequence so that we can take students from something that is really, really simple to something that is really, really complex? Like for example, today I was in a grade seven classroom and they were seeing solving one and two step equations sort of structurally for the first time. And we started with something really simple, right? Like it’s an unknown number plus 3.014 equals 7.22. What is the number? Like something really simple. And by the end of the lesson, they were solving two-step equations with decimals where we had things in denominators and stuff like that. Like they were just, they just went the whole way. But the difference between any two questions is very small, but the difference between the first question and the last question is very large.
Jon Orr: Mm-hmm. Yeah. Yeah. I guess, and maybe Kyle, you want to comment on like, what is it not? Like, and I think why I want to ask what, like why I wanted to ask what is it not is I think, I think when we have conversations with coaches and teachers and when you hear of them saying, you know, we’re doing building thinking classrooms, but when I’m walking into classrooms, it seems like the teacher’s just taking the worksheet and throwing it up on the
Kyle Webb: Yeah.
Jon Orr: And that’s building thinking classrooms. And we’re like, well, so sometimes we have to clearly say like, trying to define it because it’s like, we’re gonna thin slice these questions. We’re gonna make these small changes, which is like to a teacher. like, well, isn’t that just a worksheet? You know, it’s not, but Peter’s outlined the nuances there, but what is it to you, Kyle? What is it not?
Kyle Webb: Yeah, I mean, I it could come from a worksheet. I just haven’t seen worksheets that do a really good job of this yet. So maybe if someone’s out there working on that, that’d be great. And we can just adapt those to thinking classrooms. But like you said, it’s not a worksheet. There’s the very intentional, you know, decisions made from step to step to step, you know, start to finish, but also those incremental changes and variation from task or question to question. It’s also not what I used to love to do as a teacher is as soon as kids got momentum, I’d love to throw them a curve ball to see if they could handle the curve ball and see what the twist is. And usually it didn’t really work out. Like it’s not that, like we’re not, the curve ball might be like start to finish, it might look like a curve ball if we were to make that jump, but we’re trying to really, we talk a lot about scaffolding and education. It’s kind of a version of scaffolding. Like we’re really building slowly up, slowly up, slowly up. So it’s not that, it’s not a worksheet. It’s not these disjointed ideas that we’re trying to pull together all together at once. It’s we’re trying to very purposefully, build upon the last question, the last question. And sometimes it’s just a digit is different from one to the next. it’s, sometimes we’ll take a bigger leap when we move into like a deeper type of a question within the same task sequence, but usually there’s some sort of prompt or throwback to something earlier to make sure that they have a reference point to build upon. That’s what comes to mind when you ask that question. I actually have never thought about that. So I really appreciate that question. Peter, have you thought more about what it’s not?
Peter Liljedahl: I think it’s also not static, right? So it’s like, I’m going to build this thin slice sequence in anticipation of how well it’s going to go with my students. But then I have to be able to be nimble once I’m in the classroom with the students, right? So I was also doing a lesson today where the students, a group of eighth graders for the first time was seeing a function, y equals Mx plus B like they were seeing a y equals 3x plus 2 They had never seen that before they’ve seen 3x plus 2 equals 11, but they’ve never seen y equals 3x plus 2 and we built a sequence and I was working with the teacher and we went in and We were very dynamic in that space So we had our sequence but after every question that the kids every question we put up on the board We were having conversations watching them work like which are the next one? Is it the next one that’s on our list or is it the one after that or is it the one that’s beside the one that we put up that they need some more redundancy or we’re gonna change the order here? So it’s also not static. It needs to be dynamic as you’re engaging with the students, which is why we always say that when you have a thin slice sequence, don’t lock it into a PowerPoint, right? Because you just lose that ability to be nimble as a- students are responding to the questions you’re asking, we can anticipate how kids are gonna respond to these questions. Things that we see as small changes, they may see as no change at all, or they may see it as a huge change, right? So we have to be able to respond. The room will tell us what it needs, right? Anticipation only prepares us for like 5 % of what’s gonna happen. We gotta be ready to adapt.
Jon Orr: Right? In your opinion, like what is a, I guess a prerequisite, a non-negotiable, like what are the most important things we should be preparing ourselves for while we start to prepare a thin slicing type sequence or lesson that includes a thin slicing component? Like what are some of these? When I think about this, I think about what do we need as teachers? What should we really be focusing on? And then on the same side, if I’m a coach, I’m a coordinator, I’m like, what do I want to help my teachers the most so that they’re most prepared, they’re most positioned well to lead this type of sequence or learning routine in classroom?
Peter Liljedahl: So I’m going to start with something that Kyle said earlier. I just want to come back to that because I don’t want to get lost. This idea that, oh, this will get them. Right? Like, and I remember being that as a high school teacher too. It’s like, oh yeah, this is going to get them. Right? And it’s like, so a prerequisite is, especially when you’re trying to have the kids, because really what thin slicing is, they’re, I don’t want to say they’re learning on their own, but they’re figuring things out through their engagement with the task and then your occasional influence in that space, right? But they’re really figuring it out through the sequence of the task. And when you throw in one of those, this is gonna get them, it derails that, right? So if we’re in a space where they’re trying to learn something, know, conceptually through the experiences that they’re having, we don’t wanna derail that. So often what I say to teachers is, when you have that question that is like, yeah. I really want to use it. Don’t throw it out, but don’t use it on day one. Like that’s the kind of question you ask to see if the conceptual learning has landed, not the kind of question you use for conceptual learning. Right? It’s, it’s, it’s, we’re going to save it. We’re not going to throw it out, but we’re going to save it. Maybe it’s tomorrow. Maybe it’s the next day. Right? Let’s just, let’s, let’s keep them on this track. Kyle, do you have any other things?
Kyle Webb: No, I think that’s bang on. think when we’re thinking about making sure teachers this prerequisites, you know, skill set that you’re talking about, trying to be it’s all about being intentional, I think, right? Like a lot of thinking classrooms is just very intentional teaching. This is no different, right? Like, you need to know where you’re trying to get them to. But like Peter also said, you need to have that flexibility to be able to adapt on the fly, right? Like, we’re not putting these in permanent PowerPoints and locking these things in. We might need to be ready to go further and we might need to be ready to just stop halfway through or sorry, not stop, but like be prepared to only get halfway through, which kind of connects to some of the other pieces that we talked about in the book. We talked a lot about thinking classrooms with like the notes. We’re not saying like print those note templates before your lesson because we want you to be able to be flexible, depending on where your your students get. And if you go in expecting every student to do every single question, we’re going to have a little bit of a problem. You need to be able to allow kids to jump ahead when they. They’ve got it, otherwise they’re going to slip into boredom like Peter talked about. And if we push them too hard too early, they’re going to get into frustration and we’re going to lose that wonderful thinking and learning and productive collaboration that is so beautiful when it happens.
Peter Liljedahl: And I got, I got a few more here that are prerequisites for those people who just starting or who are doing a deep dive. there’s, there’s three things I want people to think about. One, there’s very few consequences from starting too easy. Right. So we, and I and others, the ETC team use this metaphor of we want to back the train. We want to back the train into the station far enough for everybody to get on. There’s very few consequences of backing up too far. Right. Like let’s start easy. You can always go faster. Right? You can skip things, but if it’s really hard to recover if you started too hard, like if you’re, if you’re excluding one 30 year students with the first question, that’s not good. So I have this saying that, one 30 year students should think that the first question is too easy because if one third think it’s too easy, then everybody can access it. Right? So don’t worry about starting to too easy. The second one is always over plan. I cannot tell you how many times it’s happened that the kids. It happened today in solving one and two step equations. The kids blew through my list in like 30 minutes. Well, the problem was we were going to have them at the boards for 40 minutes, right? So now it’s like, okay, I got to come up with stuff on the fly, like over plan. You’re always going to be able to use it the next day or in the future, but don’t get caught flat footed. And you know, sometimes it doesn’t matter, but sometimes it really matters what those questions are. And you know, Hopefully we’ll get to talking a little bit about the book because Kyle and I have really written that into that structure. And likewise, the third thing is trust in the wisdom of the room. Right? Like one of the things that Kyle and I talk about and what Megan and I also talked about in the previous book was the difference between prerequisite knowledge and seen befores. Right? If we’re focused on prerequisite knowledge, we’re going to spend two weeks doing review because I got to make sure that every student has this, the knowledge they need to do this unit. And it’s a, it’s a way of thinking that goes back to that time when we sat in rows and I, we were in silos and for learning to happen, we all have to have the prerequisite knowledge, but we don’t need everyone to remember everything about this topic from last year. We need them to have seen it last year. We call them seen before us. And we need to trust in the wisdom of the room. that the knowledge that some individuals have will move around the room. it’s such a powerful shift in our philosophy for planning, right? Like, do all the kids know how to add fractions? No, they’ve all seen it before. I can’t trust that they all remember it, but I trust that 10 % or maybe a third of the students remember it. And that’s often enough to get everybody doing it, right? So trust in the wisdom of the room.
Jon Orr: Yeah. Yeah. Good. That’s definitely a good message. And Kyle, and I echo your, like I constantly think about the flexibility we have to have in an environment like this and how, in a way, how we have to be masters of our, not our craft, but our content. We have to know, you know, like if we are going to craft a sequence, we have to know not only the learning goal, like your idea about intention, so important because like we get lost in the, I’m just gonna do this today, but it’s like actually you can really craft an experience that’s exceptional because you really know what the true learning goal is of this lesson on this day in this unit. But knowing the learning goal, but knowing the moves to get to that learning goal, knowing how that learning goal is useful for the next unit, the previous unit, all of these things. play a huge role in being flexible on your feet because if you don’t know how to all of a sudden whip out an area model because you need to whip out an area model or talk about this or use this strategy over here or if you just haven’t gone down the depth there, it’s sometimes the struggle. It’s like we can’t be flexible if we just don’t have that solid understanding. So we always talk about if we are gonna do something, and know, important, let’s make sure that we’re also taking time, like you said Peter, like over plan. For us, it’s like over planning is like making sure like we do the math and we understand the math and we do the math with other adults so that we can feel comfortable, like these moves make sense and I can actually feel comfortable in front of the class to be flexible because all of these moves require us to be flexible. Okay, let’s talk about the six to 12 book. Book on tasks, you know, you said you you wrote the other book with Megan Like like you’ve got you know, the main book everybody, you know Most people have read it that I that I’ve there’s not there’s not too many teachers anymore that haven’t say heard of it read it now Why this like tell me the difference? Like what do we need this book for that? The original book doesn’t do
Kyle Webb: It’s hard for me to really talk about this because I didn’t write the original book. came to no thinking. Yeah, I was waiting for Peter to do this. What I think it does offer as someone who’s read that orange book cover to cover, we’ve done podcast episodes. We’ve been doing this, living and breathing this for as long as I can remember now. The new book offers those updates to the research that has emerged since Peter initially published the book. And then the idea behind the tasks here is not so much that you have 50 tasks you can go and use because very few teachers teach all of the content that will be in the book, right? Like it’s, you can’t cover everything from six to 12 in a book, but we have little snapshots of what you can do in each grade level to hopefully give you some inspiration, show you how to do it. We’re modeling it, giving you hopefully an exemplar. I think some of the tasks, if we went back and looked at them today, we would change some things because this is ever ever-changing and ever-evolving. Every time you do it, you’re going to tweak it a little bit. So that’s what I see the book being. It’s like, here’s something similar to what you might be doing in your classroom. Build on it, tweak it, model it, see how you do it. We give you a few different styles of how to do this. Like Peter has this brilliant task that we threw in there about how we can do word problems in the context. One context, start to finish. We just continually change up little variables within the context to try to get kids more familiar with handling word problems, for example. That’s an example of how you could do. That is not in the Orange Book, but hopefully it’s something that we can provide more teachers access to and allow them to run with it.
Peter Liljedahl: And I did that task in a algebra one class down in California last week. And it’s the hot dog task, right? It’s I own a hot dog. I own a hot dog cart. The kids were fascinated by this. They wanted to know like everything there was to know about this hot dog cart that I own. And I’m setting it up all over town and I’m making different, and it’s linear relations. And we, did this with algebra one students last week. And, and there’s 30 tasks in that, in that lesson. I did not use all 30, but I was. because the lesson is over planned. I was taking what I needed and reacting to the students as they were evolving. And they were right into it, right? Like, so it’s exactly what Kyle’s saying. There’s that structure of, for example, how do we engage with word problems? But we also snuck in a couple of other little interesting things in there. So tasks is the is the premise, right? Each task is a lesson. Here’s a lesson plan. There’s 20 non-curricular, there’s 30 curricular. So we take these examples as a way to exemplify different things. So one, as Kyle said, was word problems. Another one was what does a sequence of lessons look like, right? So there’s a couple of places where we have two consecutive lessons. you can do this lesson on Tuesday, this one on Wednesday. So it’s like, what does it look like to do thinking classroom over a period of time? we, think we took a pretty interesting run at proof, geometric proof. and we have two consecutive tasks. And I actually did these ones last week as well in a geometry course. and we start with solving geometric figures and we’re solving for unknowns on the figure. And then the next day we’re working with very similar figures, but instead of, and as we’re solving them and again, the goal is to solve for them, but this time Every time you add anything to the diagram, you have to write a justification for it. Like why can you add this angle as 20 degrees? Well, that was given, okay, given. Okay, well what about this one? Well, there’s a supplementary, so I can add this as 160, right? So on day one, we’re just solving, which is the kids were right into this, but day two, and the conversations had that language in it, right? Where they’re talking to each other, why this could be added and that side has to be this and so on. but then the next day we just make it more explicit. And it’s such a much nicer way to approach proof than the two-column proof, right? The end statements and let equals this, right? And the kids were, yeah, so we’ve taken these opportunities to kind of showcase slightly different things. And we got to go all the way up to calculus. Like we have two calculus tasks in there. think we, yeah, we two great tasks. We have LCM and GCF. got a bunch of algebra functions, inequalities, both systems of linear inequalities and just linear inequalities. Like we just had, we had a lot of fun. We have weighted average. We got, what else did we have in there? I’m trying to remember now. It’s hard to remember.
Kyle Webb: I mean, there’s a lot around geometry. got a really fun one around sector areas and building on some funds. Yeah.
Peter Liljedahl: and compound areas as a way to lead them to figuring out the formula for the area of a triangle, parallelogram, and so on.
Jon Orr: Is there a topic, a strand or maybe even just a lesson that you’re like… Teachers sometimes have difficulty teaching this and they sometimes won’t think that they can do a building thinking classrooms type lesson with that. Do you guys have something that you included in that? I think high school, it’s like sometimes you’re like, well in high school we can do these types of tasks but not these types of tasks. And I think, I hear that and I’m sure you’ve heard it too.
Kyle Webb: I think the proofs that Peter was just talking about is a perfect example, right? We see that as like this, each proof is gonna take so much time. So it’s more of like, if you’re gonna do it, it’s more of a thick slice, but this, the way that we’ve set this up, I think shows you that you can do these deeper questions in an intentional sequence that allows kids to see the variation like we’ve talked about so far. And I think a lot of teachers get hung up on geometry just because of the diagrams alone. And yeah, that’s a little bit of a barrier, but we talk a little bit about how you might manage that in some of our teaching notes as part of the task.
Jon Orr: Sure, Geometry for sure. Yep.
Peter Liljedahl: So I would say we were selective, right? In order to dispel some of those. I think the proof ones and the geometry ones were exactly that. And one of the calculus one is implicit differentiation, a topic that I’m often told this won’t work. We have completing the square. Yeah, that’s not gonna work with inslicing, right? yeah, guess what? And also the word problems. And then the other one is statistics, right? Like we don’t have statistics as a task standalone, but in part four of the book, we actually show how you can use a series of probability problems, for example, to thin slice and so on. So like, we’re trying to take on some of those myths.
Jon Orr: Yeah, right. Good, yeah, no, it’s good resources for sure to have for teachers at hand. Now here’s a question that I’ve always wondered too, and it’s not I get asked this too about building thinking classrooms, is like you said, you did a couple sequential lessons, so back to back lessons to provide an example. So is it done? Did you do that on purpose to say like we’re only gonna do two or three sequences instead of a full unit that we could be using? Because I think teachers go, should I be doing this every day? Like, should I do building thinking classrooms every day? And if so, what does that look like? And do I have a unit plan to do that? I’m just curious what, like, thoughts around, like, maybe the two of you had discussions. Like, should we do a unit? Should we provide one? Or maybe not. Is there any, thoughts around that that you could shed some light on for us?
Kyle Webb: think there’s a potential slippery slope there, right? Like if we were gonna do a Unicert to finish, that might’ve been our 30 curricular tasks. really hard to go beyond. Or sorry, we get really too dialed into one specific content area and we wanted a little bit more broad, you know, offering in the book. This is one thing that I’m thinking a lot about. I’m sure Peter’s thought much more about it than I have, because I get this question a lot from teachers too. And because I’ve been out of the classroom for a while now, I haven’t done that sitting down start to finish the same way teachers are doing day in and day out. But I know teachers that are doing this day in and day out, they’re doing it every day. It might not be thin slicing every single day. They’re throwing in some rich tasks, some what we would call non-curricular tasks, but they’re finding ways to get kids collaborating in groups, on boards, using the Henson extensions. All the practices start to finish throughout the unit. Peter, have you given much more thought to this like long-term? We didn’t really have any deep conversations about this. Yeah.
Peter Liljedahl: Yeah, so, right. So one of things you’ll notice as you read it is there’s a few tasks that are like, hey, we’re in the middle of the unit and this is what the kids have seen before and let’s go. What would this look like? But a lot of them are also, hey, how would I start out this unit? Because I think we all know that if we could start out the unit right. So it gives them an opportunity to see how it can start out. But here’s the truth. Depending on where you are in the world, some of these tasks are like, If you do this task, you just covered the entire unit. Some of them are two lessons, you just did the whole unit. So for example, we have one where lesson one is factoring quadratics and lesson two is solving quadratics, finding the intercepts of quadratics and graphing quadratics. And that’s all one lesson, right? So we have two lessons and it’s like, okay, well, what’s left in this unit? We got some work out one, three, right? So it’s like, As Kyle says, there are units where it’s, yeah, we’re gonna be in there for a long time and depends on where you are in the world. But there’s other units where it’s like, I’m normally in here for a long time, but hey, we’re done. Right, so it’s the same, I would say with the trig ratio one, depending on how far that unit goes. But if we’re looking at an introduction to trig, triangular trig, not unit circle trig, we got two lessons done, right?
Jon Orr: Yeah, I 100 % agree. Folks who say I don’t have enough time to do this haven’t done it. They haven’t tried it. Because I think when you start and you’re like, oh my gosh, I did that type of lesson and I did keep going and we carefully designed it. I used one that was already made and we cover a lot of ground because of the way, the kids are doing all the work.
Peter Liljedahl: I know.
Kyle Webb: You
Jon Orr: You’re not just trying to give four examples and then going to sit down. You’re navigating this complex landscape and keeping them thinking. it’s, you know, you can cover a lot of ground. So that makes a lot of sense.
Peter Liljedahl: So often say, like, teachers will say to me, I don’t have, I have so much to cover, I don’t have time to do BTC. And my response is, you have so much cover to cover, you don’t have time to not do BTC. Right? Like it’s, you got to get them thinking if you want to get through your content. Otherwise, good luck.
Kyle Webb: Yeah, the number of teachers I work with that have been like when I was still working in my school division role, they’d email me early May, be like, Kyle, we’re through everything for the whole school year. And usually late June, they’re like, hey, Kyle, what can I get away with skipping for next year? So the teachers that are going all in on this are finding those efficiencies and they’re finding they’re getting through content much more quickly. And it’s one of those like, us, try it, and you’ll see. Yeah.
Jon Orr: Yeah. Right. Right.
Peter Liljedahl: And in part, that’s what giving these lessons in the book, these tasks is about as well, right? It’s showing that, you can do this and the kids are capable.
Jon Orr: Yeah, right, makes sense, makes sense. Gentlemen, if there is one final thought you can leave with the listener, like a big idea, like what’s the takeaway you wanna leave the listener here for today?
Peter Liljedahl: So I said earlier that thin slicing is built on two theories, right? Flow and variation theory. It’s also at its pragmatic core, it’s sorting, right? It’s sorting. That’s what Kyle and I were doing. We were sorting. We were taking tasks that we were making them, we were finding them, and we were just sorting them. And we were sorting them into a sequence. And anybody can sort, right? Like we can all sort. We build a monument to it because we’re thinking we have to make these tasks? No, right? Get the tasks and then just sort them. And we show you how to do that in the book. But if you look at the book through the lens of, these look like the tasks in my textbook. but they sorted it. That’s in many ways, that’s what we did, right? It’s sorting. Think of it as thin slicing and sorting.
Kyle Webb: Peter, that’s bang on. One of the things I’m thinking about, I have two young kids and my oldest has started kindergarten, we’re getting, know, trying to be nostalgic. We showed him some magic school bus episodes. He was really excited. And I was really inspired by the Miss Frizzle saying, take chances, make mistakes, get messy. Like I think that’s really what thinking classrooms is for me. You got to get in there. You got to try it. If you’re expecting perfection, or if you’re expecting to take one of our lessons out of this book and use it, and it’s going to go absolutely perfect the first time. It’s not gonna happen. You gotta be okay to get in there, try it, find your efficiencies, make it your own. And that’s gonna be the same with every task that you do in a thinking classroom.
Jon Orr: Awesome.
Jon Orr: Great message, great message. Two more takeaways. One is this book, it’s not out yet guys, it’s not out. It’s coming out in, you said October I think, so by the time you listen to this, it’s probably out there. You can go and get yourself a copy. Give us the name so that everybody knows where to go find it.
Peter Liljedahl: Give it two more weeks.
Kyle Webb: Yeah.
Kyle Webb: Ahem.
Peter Liljedahl: Math tasks for the thinking classrooms, six to 12. It’s Burgundy if you’re north of the border, it’s Maroon if you’re south of the border. I don’t know why. And it’s at the printers right now. It is being, it’s starting to ship in two weeks. Shipping to the warehouses, yeah.
Jon Orr: Hahaha
Jon Orr: Awesome.
Jon Orr: Awesome, second takeaway, right? Yeah, second takeaway is these two gentlemen are gonna be presenting at the seventh annual 2025 McMath Moments Virtual Summit in November. Tickets are available right now. You can register, it’s completely free the entire weekend. Go and register yourself and join 50 other speakers throughout the weekend for a fabulous weekend of learning. So we’re looking forward to seeing you two there. Thanks everybody for joining. Thanks Peter, thanks Kyle for joining today.
Peter Liljedahl: Thanks for having us.
Kyle Webb: Bet can’t wait for the summit.
Thanks For Listening
- Book a Math Mentoring Moment
- Apply to be a Featured Interview Guest
- Leave a note in the comment section below.
- Share this show on Twitter, or Facebook.
To help out the show:
- Leave an honest review on iTunes. Your ratings and reviews really help and we read each one.
- Subscribe on iTunes, Google Play, and Spotify.
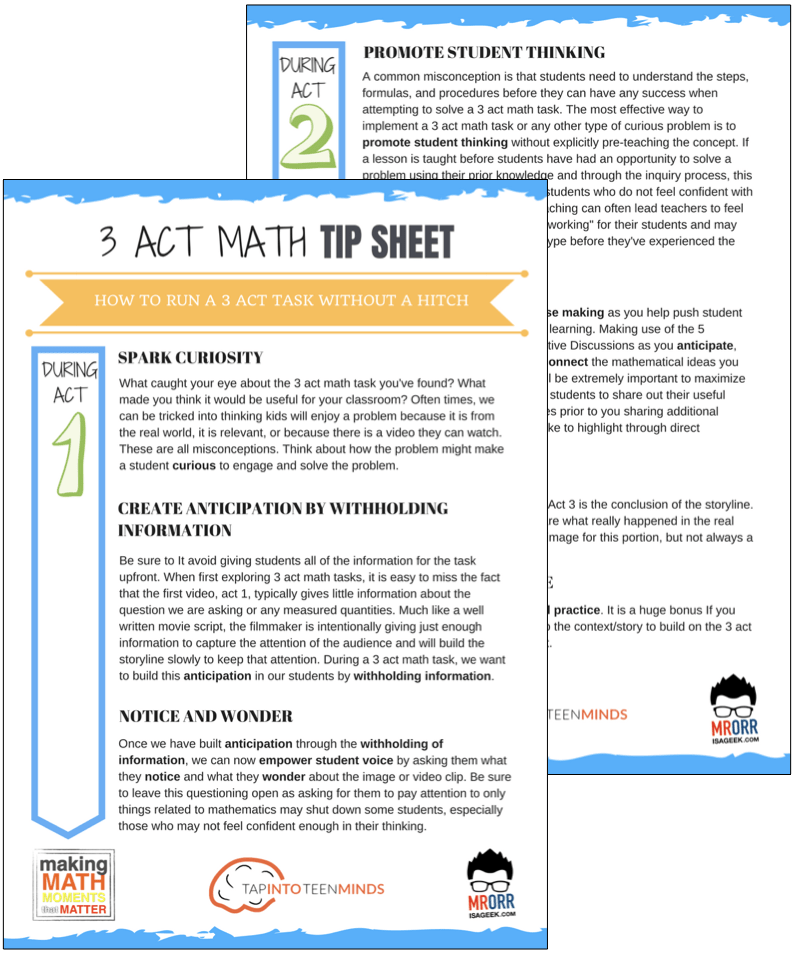
DOWNLOAD THE 3 ACT MATH TASK TIP SHEET SO THEY RUN WITHOUT A HITCH!
Download the 2-page printable 3 Act Math Tip Sheet to ensure that you have the best start to your journey using 3 Act math Tasks to spark curiosity and fuel sense making in your math classroom!
LESSONS TO MAKE MATH MOMENTS
Each lesson consists of:
Each Make Math Moments Problem Based Lesson consists of a Teacher Guide to lead you step-by-step through the planning process to ensure your lesson runs without a hitch!
Each Teacher Guide consists of:
- Intentionality of the lesson;
- A step-by-step walk through of each phase of the lesson;
- Visuals, animations, and videos unpacking big ideas, strategies, and models we intend to emerge during the lesson;
- Sample student approaches to assist in anticipating what your students might do;
- Resources and downloads including Keynote, Powerpoint, Media Files, and Teacher Guide printable PDF; and,
- Much more!
Each Make Math Moments Problem Based Lesson begins with a story, visual, video, or other method to Spark Curiosity through context.
Students will often Notice and Wonder before making an estimate to draw them in and invest in the problem.
After student voice has been heard and acknowledged, we will set students off on a Productive Struggle via a prompt related to the Spark context.
These prompts are given each lesson with the following conditions:
- No calculators are to be used; and,
- Students are to focus on how they can convince their math community that their solution is valid.
Students are left to engage in a productive struggle as the facilitator circulates to observe and engage in conversation as a means of assessing formatively.
The facilitator is instructed through the Teacher Guide on what specific strategies and models could be used to make connections and consolidate the learning from the lesson.
Often times, animations and walk through videos are provided in the Teacher Guide to assist with planning and delivering the consolidation.
A review image, video, or animation is provided as a conclusion to the task from the lesson.
While this might feel like a natural ending to the context students have been exploring, it is just the beginning as we look to leverage this context via extensions and additional lessons to dig deeper.
At the end of each lesson, consolidation prompts and/or extensions are crafted for students to purposefully practice and demonstrate their current understanding.
Facilitators are encouraged to collect these consolidation prompts as a means to engage in the assessment process and inform next moves for instruction.
In multi-day units of study, Math Talks are crafted to help build on the thinking from the previous day and build towards the next step in the developmental progression of the concept(s) we are exploring.
Each Math Talk is constructed as a string of related problems that build with intentionality to emerge specific big ideas, strategies, and mathematical models.
Make Math Moments Problem Based Lessons and Day 1 Teacher Guides are openly available for you to leverage and use with your students without becoming a Make Math Moments Academy Member.
Use our OPEN ACCESS multi-day problem based units!
Make Math Moments Problem Based Lessons and Day 1 Teacher Guides are openly available for you to leverage and use with your students without becoming a Make Math Moments Academy Member.
Partitive Division Resulting in a Fraction
Equivalence and Algebraic Substitution
Represent Categorical Data & Explore Mean
Downloadable resources including blackline masters, handouts, printable Tips Sheets, slide shows, and media files do require a Make Math Moments Academy Membership.
ONLINE WORKSHOP REGISTRATION

Pedagogically aligned for teachers of K through Grade 12 with content specific examples from Grades 3 through Grade 10.
In our self-paced, 12-week Online Workshop, you'll learn how to craft new and transform your current lessons to Spark Curiosity, Fuel Sense Making, and Ignite Your Teacher Moves to promote resilient problem solvers.










0 Comments