Episode #391: How To Help Students Choose the Right Math Operation
LISTEN NOW HERE…
WATCH NOW…
It’s a familiar challenge— when it comes to deciding which math operation to use, students get stuck. In this episode, we explore one of the often overlooked reasons: a lack of understanding around mathematical structure and behaviour.
We dive into what’s really needed for students to confidently choose the appropriate operator, with a focus on structure—not only strategies or models. Using division and subtraction as examples, we highlight the different images, actions, and interpretations that shape how students approach problems—and why recognizing these distinctions is essential for meaningful math learning.
In this episode, you’ll discover:
- Why students often struggle to select the appropriate math operator
- The critical role of understanding mathematical structure and behaviour
- How different interpretations of operations like division and subtraction can confuse students
- Practical steps teachers can take to support better operator selection
- The teachers role to connect the behaviour to the symbolic representation
Attention District Math Leaders:
Not sure what matters most when designing math improvement plans? Take this assessment and get a free customized report: https://makemathmoments.com/grow/
Ready to design your math improvement plan with guidance, support and using structure? Learn how to follow our 4 stage process. https://growyourmathprogram.com
Looking to supplement your curriculum with problem based lessons and units? Make Math Moments Problem Based Lessons & Units
Be Our Next Podcast Guest!
Join as an Interview Guest or on a Mentoring Moment Call

Apply to be a Featured Interview Guest
Book a Mentoring Moment Coaching Call
Are You an Official Math Moment Maker?

FULL TRANSCRIPT
Yvette Lehman: I was in a room recently with educators from K to 12, and we were trying to come up with a common goal for what’s a critical need in the system right now. And one of the things that emerged was this idea that whether students are in grade two or grade seven or grade 10, the inability to necessarily select the appropriate operator is something that we’re observing in student behavior.
I often always say this, used to teach grade six and on our standardized assessment, they can use a calculator. And I used to always say like that calculator is only helpful if you know the operator.
Jon Orr: if you know what to push. I know to push plus or subtract.
Yvette Lehman: Right? Or I even know, you know, in a division sentence, like what’s the dividend and what’s the divisor. Or, you know, right. Yeah.
Kyle Pearce: Yeah, and it would be even better if you, yeah, if you in your mind though too also had like some sort of like general idea, like a range of like what might be reasonable, you know, like I feel like it’s this understanding of what it is that we’re trying to do and you’re just looking for maybe a little more efficient way to get an exact answer, but it’s like in our minds we should have like some sort of general understanding of what’s about to happen.
Jon Orr: Which one do I put first, the bigger one?
Kyle Pearce: And I think that’s kind of what we’re going to get at here is like sort of like knowing more than what the operator is and more about like what happens when we do things in mathematics.
Jon Orr: Right, but I mean, like you think about teachers right now, you constantly hear that kids struggle with application problems, word problems. How do I actually do problem solving? And this speaks clearly to the heart of that, is that why kids are probably struggling immensely with that is this issue. Is that when do I pick this? When do I pick that? Like how do I know? And then like,
old solutions. You know where I’m going to go with this Kyle and Yvette is like, teachers used to be like, well, let me help you with better problem solving and selecting it because I’m going to give you a highlighter and you’re going to look for the keywords, you know, like to say like, look for that keyword that will tell you what operator to pick. But that’s not the solution here. So let’s dig in. Yvette, let’s do it.
Yvette Lehman: think that may be part of my own struggle when I was supporting students to do this work is that my understanding of the operators and what they do was too narrow.
So when I think, so subtraction is the perfect example. And I would argue that if I walked into a school tomorrow, any school across North America, and I stopped teachers and students in the hallway and I said, tell me what subtraction means, tell me what subtraction does. I mean, I haven’t done this yet, but I think I should. I feel like I’m going to hear over and over and over again, take away, take away, take away, take away. And I think that maybe this
Jon Orr: Take away, take away, just take away.
Yvette Lehman: lack of understanding of the behaviors of the operators or making them far too narrow for what they actually do is part of the confusion or part of the struggle that we’re facing in classrooms. I love this quote by Van de Waal and it’s about division. And of course, you know, we could do a whole, we’ve done a whole episode on division and the behavior of division, but I think that this quote is not just about division. Like you could replace it with subtraction, with multiplication, with addition. And it says, consider the question, what is division?
As a teacher, you need to be aware of the different images and actions involved in division and recognize that different interpretations are experientially distinct from one another and not applicable in every situation. And the one word that really jumps out to me is like experientially distinct. Like they behave differently.
Kyle Pearce: Yeah. Right? Like what, what I, if you want to summarize that entire statement in one word, it’s it, or I guess it’d be two words. It’s like, depends, you know, like, you know, where it’s sort of like, there’s no like all in one, this is what you do when we divide. It’s like, there’s so many different ways that division can behave depending on the situation that you’re working within. And I think
We, I think I didn’t have an awareness of that for so long, even though I was doing it just through probably automaticity, right? And maybe not really understanding why in many cases. So I like that, but today we’re not talking about division. Where are we gonna talk about, like what topic or what concept are we gonna be digging into in order to kind of highlight this quote?
Yvette Lehman: subtraction. I mean, I obviously, it’s my second favorite operator after division, but I think subtract, for sure. Yeah. Yeah, we’re not, it’s, yeah, that sounds right. Yeah. Cousins. You’re right. Yeah. I agree. So I like subtraction because I think that you mentioned the word awareness and I think that I wasn’t even aware of how much I didn’t know about subtraction. Like I thought I had a handle on subtraction, yet students struggle with it.
Kyle Pearce: I mean, they’re kind of like brothers and sisters, you know what I mean? Like they, you know, they like to, they, yeah, yeah, yeah, for sure. Cousins works. Okay. That’s fine. Yeah.
Jon Orr: I like they’re cousins, they’re cousins.
Yvette Lehman: Like I don’t know that I have talked to many first through fifth grade teachers who are like subtraction’s not a problem. Like we’re good, know, students know how to subtract. I remember Kyle, do you remember when we went down the Marion Small journey of subtraction structures? And at that time we basically, through her work and support, we were able to identify, let’s say four predominant structures or behaviors of subtraction.
So like the first one is that change scenario, which is like the separator, takeaway. Then for sure. Yeah. So in like that scenario, it’s like there, you have a hundred dollars, you spend $3. How much do you have left? $97. Then you have, I think probably the, I don’t know, the one that has the greatest impact later on that gets the least amount of attention.
Kyle Pearce: Yeah, most common, most comfortable for everyone.
Yvette Lehman: which is compare, like just thinking about subtraction as comparison. And we’re looking at the difference between two quantities.
Kyle Pearce: Well, it’s almost like an early bridge to like relative thinking, right? Because it’s like you have to relate the quantities to one another. that comparison is like without that, it’s hard to take that next step into multiplicative thinking, right?
Yvette Lehman: Well, and even when you’re doing that multiplicative comparison, like sometimes, for example, when we’re looking with indirect variation equations, like linear equations, and you’re looking at two quantities of the same variable, you actually need to look at it. You need to look at the change. So you’re like, OK, so if it starts at four and goes to 40, the change here is 36. And then I can use my, you know,
understanding of rate and division to make sense of that. So for sure, like there’s significant implications for comparison later, but that’s not the only two. There’s also some algebraic structures where it’s like part, part, whole, but you’re missing a part. So you have a missing addend. And then we also have the scenario where you have a missing subtrahend, where it’s like a subtraction scenario. So the example we often give for that, it’s like, I had 20 cookies in the jar. I walked away, I came back, now there’s only 15 cookies in the jar. How many were eaten?
Jon Orr: Hmm. Right. I don’t know how many to take away. not looking for the answer. It’s like I know the answer.
Kyle Pearce: Who took, yeah, who took the cookies? And that’s very connected to algebraic thinking, like having an unknown and kind of working with an algebraic equation.
Jon Orr: Very much so. It’s almost like it, you know, exactly. It basically defines an equation that you could write.
Yvette Lehman: And I think that maybe the reason that we in general, you know, struggle with subtraction and struggle with division is because again, we’re defining it in such a narrow way and we’re not as Vanduul describes, like talking about the different images and actions they create, like exploring with intention all of these different scenarios, actually living them, breathing them. And then as Kathy Fosna would suggest, it’s like, then you put the
symbolic representation to match the context. So here’s my example that happened to me yesterday. So Leto is 10 and he just got a new Lego and I asked him if it was the Lego he’s built with the greatest number of pieces. So then he’s looking up, you know, all the other Legos he’s built and how many pieces they were. then like immediately he’s telling me the difference.
He’s like, this one is 198 more than the last one I did. This one’s 217 less. He’s naturally exploring this comparison subtraction scenario, but my job is to help him see that that is subtraction. Like I write. It wasn’t though. Like he was doing that very intuitively, but if I said to him for sure, yes.
Kyle Pearce: is what you are doing here. seems obvious, but…Sorry, mean coming up with the answer feels obvious and you’re like you don’t really know why it’s just it’s just happening and I know the answer but I can’t articulate why you
Yvette Lehman: So imagine as he’s doing that, like that he was curious about this, I said to him, okay, let’s write an equation to represent what you just did. Like I need him to be able to associate the behavior with the symbolic representation.
And I think that’s the piece that I need to strengthen where it’s like, can put students in situations that are really relevant and their reasoning and they’re curious, but then I’m the one who has to explicitly tie it to the symbolic and help them see that that behavior is subtraction. Let’s do another one. Let’s think of another scenario that that’s that type of subtraction. Can we name it? Can we categorize it?
Kyle Pearce: Right. And that’s that modeling piece that’s really important for the educator. You know, we see this happen a lot with, number talks, you know, when when people are doing math talks and educators are doing great things, kids are reasoning, they’re coming up with ideas. But then it’s like we need to show them what that looks like structured so that students can kind of go, like when I think like this, it can be represented like that. And eventually, just like a language, because math is a language.
you get to they can start to represent it that way themselves also. Right. And that’s I think that’s I’m having a little mini epiphany here with with this idea that it’s like doing the math in the car, for example. These are all great things to do. But if we’re not being very explicit with students and with our children as to what that also looks like or sounds like or what it could be represented as, we’re missing an amazing opportunity.
that could be super helpful for them when they step into other mathematical situations.
Jon Orr: Well, as you as you describe, you know, being explicit, because, you know, as a teacher, my mind starts to go like, well, what does that lesson look like? Like, like, how does that how do we structure that lesson? Like, what are the learning goals that we’re striving for? Because I think what you’re saying is that maybe old you may have would have been like, let me put them in a scenario, and then we’ll we’ll we’ll model it, you know, we’ll model it, but I maybe wasn’t explicit about what type this was, and how, you know, this is actually this. And then let’s compare it to the like, like having
specific lessons, specific learning goals, specific targets and success criteria built around them to help you identify what am I looking for from a student who gets this and gets this component? And how do I create a lesson or an experience for that student to actually come, be able to understand it, be able to recognize it, be able to do it, be able to model it with an equation, be able to
to be able to kind of use it in the way that we want them to be thinking about this. Like that’s in a way so much deeper than I think what we tend to think about when we think about using operators. Because if we think about like just saying like, let’s just do it over and over over and over again in the worksheet. Like I remember talking with Jenny Bay Williams about worksheets, with about practice. And she was adamant that there’s nothing wrong with a worksheet.
as long as or obviously the practice is essential, but it’s like, if the worksheet or the practice has to be able to like help you in the student be able to select or select the appropriate strategy, because if we’re trying to help students be fluent around subtraction, and we want them to know that difference is subtraction, and sometimes we see difference and sometimes we see change, then it’s okay to like,
put different problems in front of kids and be able to practice. Whether it’s a worksheet or whether it’s an activity that you’re working with, whether it’s small group or a game, we want them to be able to like experience those and practice those as long as they’re making say that connection as to what your learning goal is.
Yvette Lehman: I think you brought up a good question of what does this actually look like? So let’s unpack, example, our missing subtrahend scenario. So that scenario, students in first, second grade could figure that out. It’s a part, part, whole scenario, right? They had 20, now they have 15. They’re trying to figure out the part that’s been removed. What they may not be able to do is represent that as 20 minus variable for unknown equals 15. That’s my job.
Like my job is to help them see that that is what they just did mathematically. And then what I would do is give them now the, so we did the scenario and I emerged the equation. Then I would give them an equation and have them play out the scenario. So it’s like, we really need to be working back and forth constantly. And I wonder too, if I’m imagining in my grade one or two classroom, I have these, you know, different structures for addition and subtraction on
boards around my room with examples and every time we explore a context we start to name where it would fit. Like what is it most like? Is this a joining problem? Is this a separating problem? Is this a compare problem? Is this a part-part-whole problem? Then students could make up their own problems and put them up under those different categories. Like I just, think that we need to, and this has worked for me as well, just to be super intentional that
there’s a behavior to these operators, but then also make that connection to the symbolic representation. And I really feel this with my own kid. I think he is amazing at reasoning, but then he looks at a division problem and he says to me, I don’t know how to divide because he’s not yet looking at a division equation and making up a scenario in his head that could be represented by that equation.
Kyle Pearce: Right, right. It’s like reading, you know, like you don’t show kids words and then try to get them to understand what those words mean. But in math, we do that quite a bit. So it’s like we show a division sentence and then we try to like back map it to what it really means when in reality, it’s like kids already have these experiences. They already have the reasoning. They already have the…
the ability to do a lot of this work and what we need to do is sort of show them that they’re already dividing. And that’s sort of the big takeaway I’m getting here is like, regardless of the operation, regardless of what math action we’re trying to take here, basically what we need to do is we need to get kids doing those things and then showing them that what they’re doing can be written a different way.
And then, and only then does it make sense for us to now start with the abstract and then starting to kind of work our way backwards to show, Hey, now can you work backwards to show us the reasoning behind this symbolic representation? Right. And, know, we’ve talked about it many times before. It hasn’t come up quite, quite as often, but this idea of the CRA model or concreteness fading, we explored back in greater Essex, the idea that we need to start with.
things in the concrete, also like where we’re comfortable and where we are already reasoning and understanding. And we can add structure to it slowly but surely. And then once we’re there, we can then kind of work our way backwards and work from the symbolic all the way back. And I think, I don’t know, for me anyway, I’m sort of like looking at it slightly different than I did before I walked into this conversation here today.
Yvette Lehman: I have a few calls to action, I think. I think our first call to action is to familiarize ourselves with the structures and behaviors of the different operators. I would say if you’re gonna start anywhere, start with division and subtraction. They’re the most complex, which is likely why they cause the most difficulty in our elementary classrooms. In the Ontario curriculum for grade two, there’s an appendix under expectation B 2.4.
And it’s a chart basically that talks about these different addition and subtraction structures and then provides examples of both word problems as well as the symbolic representation. So that might be a good place to start. The other call to action is if you’re thinking to yourself, I want to be a stronger facilitator of the person who
shows the mathematical language. So it’s like I’ve put them in a context, I’ve allowed them to reason through a problem, but now I’m the one who has to connect the representation to the symbolic to strengthen their understanding. My best professional learning on how to do that was reading Cathy Fosno’s Conferring with Young Mathematicians at Work. That is like the heart of that book of how you create context and then you as the teacher.
make the connections so that students see that their reasoning can be represented symbolically and how that looks through the consolidation. So if anybody’s looking for a summer read, that’s one of my go-to books that’s had the greatest impact on my facilitation of this type of learning.
Kyle Pearce: I love that call out and that shout out. Actually, John and I were just on a call with Cathy earlier this week, got to check in with her and Ryan, fantastic team over there. John, I think we got a verbal yes for them joining us for the virtual summit this November, which is fantastic. We always love having them. And that read is a great read, even if you’re not a great reader like me. So definitely worth digging into.
Jon Orr: Folks, today we spent this time to strengthen our own understanding of our proficiencies for math. And hopefully, you’ve also had a glimpse of how we need to, or the benefit of strengthening those proficiencies. So when we think about our classroom trees, when we think about our own growing tree, we’re talking about the roots. The roots are our own mathematical proficiencies. We have to be strong.
on that side, if we were going to be flexible in the classroom with our teaching moves, our branches. If we’re going to be helping our students shape their mindset, which are the soil, the water, the sunlight of our classrooms, we have to have those strong roots. And the event’s got two important call to actions here for you to take a step forward in to strengthen those roots. If you want to know more about your classroom tree, head on over to makemathmoments.com forward slash report.
MakeMathMoments.com port slash report, fill out assessment there to see where the pieces of your tree fall and how to strengthen each of those six components of an effective classroom and classroom tree.
Thanks For Listening
- Book a Math Mentoring Moment
- Apply to be a Featured Interview Guest
- Leave a note in the comment section below.
- Share this show on Twitter, or Facebook.
- Leave an honest review on iTunes. Your ratings and reviews really help and we read each one.
- Subscribe on iTunes, Google Play, and Spotify.
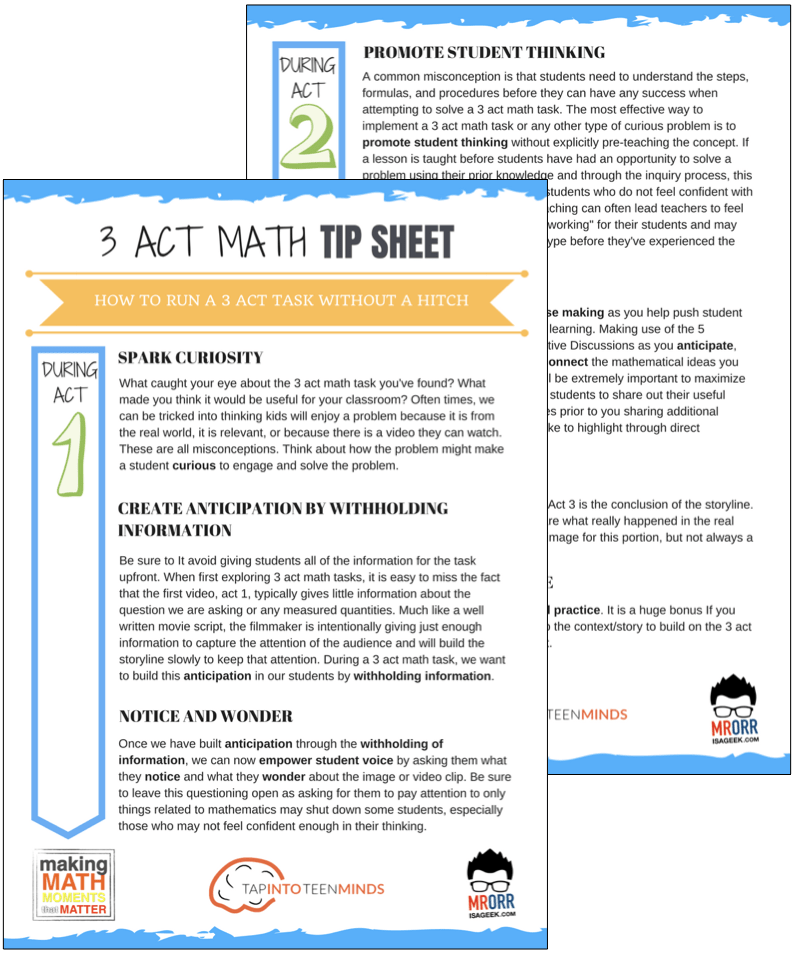
DOWNLOAD THE 3 ACT MATH TASK TIP SHEET SO THEY RUN WITHOUT A HITCH!
Download the 2-page printable 3 Act Math Tip Sheet to ensure that you have the best start to your journey using 3 Act math Tasks to spark curiosity and fuel sense making in your math classroom!
LESSONS TO MAKE MATH MOMENTS
Each lesson consists of:
Each Make Math Moments Problem Based Lesson consists of a Teacher Guide to lead you step-by-step through the planning process to ensure your lesson runs without a hitch!
Each Teacher Guide consists of:
- Intentionality of the lesson;
- A step-by-step walk through of each phase of the lesson;
- Visuals, animations, and videos unpacking big ideas, strategies, and models we intend to emerge during the lesson;
- Sample student approaches to assist in anticipating what your students might do;
- Resources and downloads including Keynote, Powerpoint, Media Files, and Teacher Guide printable PDF; and,
- Much more!
Each Make Math Moments Problem Based Lesson begins with a story, visual, video, or other method to Spark Curiosity through context.
Students will often Notice and Wonder before making an estimate to draw them in and invest in the problem.
After student voice has been heard and acknowledged, we will set students off on a Productive Struggle via a prompt related to the Spark context.
These prompts are given each lesson with the following conditions:
- No calculators are to be used; and,
- Students are to focus on how they can convince their math community that their solution is valid.
Students are left to engage in a productive struggle as the facilitator circulates to observe and engage in conversation as a means of assessing formatively.
The facilitator is instructed through the Teacher Guide on what specific strategies and models could be used to make connections and consolidate the learning from the lesson.
Often times, animations and walk through videos are provided in the Teacher Guide to assist with planning and delivering the consolidation.
A review image, video, or animation is provided as a conclusion to the task from the lesson.
While this might feel like a natural ending to the context students have been exploring, it is just the beginning as we look to leverage this context via extensions and additional lessons to dig deeper.
At the end of each lesson, consolidation prompts and/or extensions are crafted for students to purposefully practice and demonstrate their current understanding.
Facilitators are encouraged to collect these consolidation prompts as a means to engage in the assessment process and inform next moves for instruction.
In multi-day units of study, Math Talks are crafted to help build on the thinking from the previous day and build towards the next step in the developmental progression of the concept(s) we are exploring.
Each Math Talk is constructed as a string of related problems that build with intentionality to emerge specific big ideas, strategies, and mathematical models.
Make Math Moments Problem Based Lessons and Day 1 Teacher Guides are openly available for you to leverage and use with your students without becoming a Make Math Moments Academy Member.
Use our OPEN ACCESS multi-day problem based units!
Make Math Moments Problem Based Lessons and Day 1 Teacher Guides are openly available for you to leverage and use with your students without becoming a Make Math Moments Academy Member.
Partitive Division Resulting in a Fraction
Equivalence and Algebraic Substitution
Represent Categorical Data & Explore Mean
Downloadable resources including blackline masters, handouts, printable Tips Sheets, slide shows, and media files do require a Make Math Moments Academy Membership.
ONLINE WORKSHOP REGISTRATION

Pedagogically aligned for teachers of K through Grade 12 with content specific examples from Grades 3 through Grade 10.
In our self-paced, 12-week Online Workshop, you'll learn how to craft new and transform your current lessons to Spark Curiosity, Fuel Sense Making, and Ignite Your Teacher Moves to promote resilient problem solvers.










0 Comments