Episode #380: How To Unpack Math Standards with Teachers: The Strategy Every Math Team Needs
LISTEN NOW HERE…
WATCH NOW…
Math curriculums and standards are more ambitious than ever—often asking teachers to cover more than a year’s worth of learning in less than 10 months. Many districts have wisely taken the first step by identifying priority math standards. But the real magic happens in what comes next: unpacking those standards.
In this episode, we dive into what it really means to unpack a math standard. We’ll model the process using an example focused on exponents and powers to make this abstract concept concrete. Whether you’re a classroom teacher, coach, or system leader, you’ll leave with actionable strategies to support your team in turning ambitious standards into focused, achievable learning goals.
In this episode, you’ll discover:
- Why ambitious math standards often overwhelm both teachers and students
- The importance of identifying priority or power math standards
- What “unpacking a math standard” actually involves
- How unpacking builds clarity and coherence across grade levels
- A step-by-step model using exponents to show unpacking a math standard in action
- Tips for using collaboration and teacher teams to deepen math curriculum understanding
Attention District Math Leaders:
Not sure what matters most when designing math improvement plans? Take this assessment and get a free customized report: https://makemathmoments.com/grow/
Ready to design your math improvement plan with guidance, support and using structure? Learn how to follow our 4 stage process. https://growyourmathprogram.com
Looking to supplement your curriculum with problem based lessons and units? Make Math Moments Problem Based Lessons & Units
Be Our Next Podcast Guest!
Join as an Interview Guest or on a Mentoring Moment Call

Apply to be a Featured Interview Guest
Book a Mentoring Moment Coaching Call
Are You an Official Math Moment Maker?
FULL TRANSCRIPT
Yvette Lehman: We often hear leaders and teachers talking about how ambitious and lofty the curriculum or standards are. like this is, research also suggests this, right? That many people have analyzed the curriculum and really made the conjecture that there’s more than 10 months of learning packed into all of those standards and expectations. It’s a lot, you know, and it often feels daunting. And so a move that many districts have made is
Jon Orr: I’ve got too many standards to teach.
Yvette Lehman: to go through all of those standards or expectations and identify the high leverage ones. Some people call them the priority standards. It’s like, are the ones that are critical key concepts at this grade level that students need to develop mastery of in order to be successful long-term. If you’re running out of time or you’re trying to use your time strategically, make sure that you are emphasizing these key concepts.
Jon Orr: Yeah, or like, or like, these are the key key concepts that we want to like, and this is some of the other work that some of the districts that we support doing is like, which key concepts do we want to like see stretch vertically? And then therefore, we can’t we want to make sure that we’re giving our students in those key concepts at that grade level, you know, emphasize, you know, certain strategies, maybe certain models that we know are going to be impactful.
to make sure that that becomes the priority so that it carries on to the next grade level and the next grade level and the next grade level. think like people right now are going like I know some of those key standards are for my grade level that do stretch vertically. So like we can’t afford to you know be deficient in these areas or what it means is like we know these are really important therefore if we do have time to support teachers on standards which standards are there it’s these ones.
Yvette Lehman: Absolutely. I think the challenge though that many districts face with this workaround priority standards is like who is doing the heavy lifting to identify the priority standards? Who is creating the document? Thinking about the learning goals. It’s usually a small central office team. Because who you know teachers who are teaching all day don’t have the time to do this, you know, high cognitive demand task. But.
Just like we always say in the classroom, it’s like, the person doing the work is the one who is doing the thinking and doing the learning. And so now I’ve created this document. I’ve identified this, you we have, let’s say hundreds of standards in the main curriculum. Okay, now I’ve whittled it down to 10 to 20 that are absolutely critical. But what we’re gonna unpack here today is now what?
So we’ve identified them, but now what’s the next step to strengthen teaching and learning around these big ideas?
Jon Orr: Yeah. What does that look like? Like if I have to do professional development or not have to, but if I get to, right, if I get to do professional development on those standards, like how do I strengthen those standards up? That’s, that’s the question.
Yvette Lehman: where we’re starting to see some successes through really intentional use of embedded teacher collaboration time or PLCs, where protocols are in place, where teachers come together collectively with a skilled facilitator, and the work that they’re engaging in is sometimes referred to unpacking the standard. But my question is, what does that mean?
Jon Orr: What does unpacking the standard mean? Yeah.
Yvette Lehman: Right, right. And there’s probably more multiple ways to interpret that, but I’m just curious and I’m wondering for this community, what does that mean to you to unpack the standard?
Jon Orr: Right. Yeah. Like, it mean like we’re just we’re looking at the standard and trying to go like, what does it actually tell? Like, what is this document that, you know, we actually is it actually saying on how in depth do we go? I know here in Ontario, when we know the curriculum shifted, especially for the grade nine curriculum, it shifted. And, you know, we know it was unveiled this is new curriculum since there was no textbooks to go with it. And at the time,
it didn’t go into say, the specific expectations in depth. So it left many teachers and many school districts wondering like, how far do we go with, you know, this this part of linear relations or this this part. So it’s like you had some schools at that time, going very deep, and then some schools kind of being in a way not so deep. And it was because we weren’t sure because we were all interpreting, like we’re unpacking a standard and going, well, but where do we how far do we take it? What is that standard specifically?
telling us and here’s probably what most districts and most schools end up doing, right Yvette? Is that they’re like, we do have a textbook. Let’s just look at that. And that’s unpacking the standard and going, I’ll just grab what someone else’s interpretation of the standard is and I’ll use that because it’s quick, it’s quick, it’s easy.
Yvette Lehman: So what we’re going to do here today, John, is we’re just going to on the fly, unpack a standard together. Selfishly, this is for me because I need your support in unpacking this standard. So I’m going to put you on the spot. Okay. I’ve identified a standard for us. It actually originally stemmed from a conversation with one of our partners based in Louisiana. So I’m going to read you the grade eight standard in Louisiana, but then I’ll share the grade nine Ontario standard that is basically the same thing.
So in grade eight in Louisiana, it says, know and apply the properties of integer exponents to generate equivalent numerical expressions. Okay. And here in Ontario, this comes up in grade nine, it says, analyze through the use of patterning, the relationships between the exponents of power and the operations of power, and use these relationships to simplify numeric and algebraic expressions. Okay.
So if I was going to unpack a standard, the first thing that I personally like to do, and as I mentioned, there’s not one way to do this, but this is just my process, is I like to start by identifying what is the student learning goal? What are we really asking of students? What’s the lasting and enduring understanding? So if you and I were collaborating in a PLC, we’re, you this is our mock PLC right now, how would we articulate in student-friendly language what it is we’re hoping to achieve?
Jon Orr: And I think what your default is is like, let me take the standard and just rewrite it so that the student says, you know, by the end of the year, my students will know and apply properties of integer exponents to generate equivalent numerical expressions. that’s the typical, I think what happens in say our PLCs is like, that’s my learning goal, which I, and ultimately it is your learning goal because it is the standard. We want that to be the takeaway that we students can know and apply the properties of integer exponents. But I think
we need to kind of go, what is the purpose here? Like the standard is written, but is there any sort of component here that we want to have our students take away? Like what are those, I think you used the term residue, or what is this belief or this truth that we need them to have that’s attached to this? Sometimes it’s like asking, well, why is that important? What does it help?
our students kind of know and understand do about say the relationships in mathematics. Ontario’s description is a little bit more like try it this way. You know, it’s like not say like, hey, just do this. It’s like, do this, but make sure you use patterning because we really were trying to like strategically guide you to not just show that, teach the rules because the rules are really quick. The rules, but then it doesn’t get at like the reason, which is where patterning comes in for this particular standard of like, we can look at the patterns that are evolving.
Yvette Lehman: Mm-hmm. Yeah, it’s through patterning. Teach the
Jon Orr: you know, we can then generalize to make our own rules. That’s where Ontario’s trying to go versus say Louisiana state standard.
Yvette Lehman: So my question would be, you know, we’re working with all four operators. Okay, that’s my interpretation of this standard. I think that what we want students to able to do is to understand equivalent expressions for the purpose of simplifying in order to solve. So it’s like, how can I simplify this expression so that it’s more manageable for me?
Jon Orr: Right. So yeah, something that always stuck with me is, and this is specifically about like how you can structure your lessons as well, because that’s part of the, you you’re unpacking the standards so you can decide on what is my structure of my lesson that best helps teach the students that lesson or that learning goal or that standard. And, you know, I often remind of, especially when we are working in very abstract land, like where, you know, exponent rules, sometimes, you know,
Yvette Lehman: It makes more sense to me.
Jon Orr: Tendulai is like, do I teach this with context? Or how do I teach this so that there is the patterning happening here that I can get my students to explore? Which is, you know, that quote, or a quote from Dan Meyer, which is basically, if math is the aspirin, what’s the headache? You know, and that part, if you can ask yourself that when unpacking a standard, sometimes can get at those pieces of like, well, what is the why here? Like, why are we exploring this? Because that can also help you structure your lesson plan to get at
if math is the aspirin, like basically if knowing and applying the properties of integer exponent rules to create expressions, equivalent expressions is the aspirin, what makes this, like why do that? Like what is helpful to do that? And that can, for us that’s always been like how you can develop the context of the problem if you’re gonna say bring in a lesson to support this standard and set the stage for that next move. But also helps you unpack.
the standard itself because that’s the key component here, right? It’s like we need to understand the standard ourselves and these answers to these questions so that we can then translate into students.
Yvette Lehman: So part of our process would be to actually articulate, you know, that learning goal, like you said, like, what is it? What is it we’re trying to tackle here? What are we trying to enroute? Do you feel confident yet? Like, I feel like we’re trying to pack this learning into a short episode, but I feel like I’m leaning towards something like, I will understand that, I don’t even know if I want to say knowing, but you know, using…
the relationships that exist between exponents and their powers. There’s two things here, right? You have the relationship between the exponent and its power, but then also the operators. It’s like two.
Jon Orr: Yeah, that’s like, basically what you’re trying to say, right, is we’re saying like, we’re using operations specifically multiplying and dividing with powers with the same base. if we’re multiplying dividing powers that all involve the same base, how can I use my, patterning that exists in here to simplify expressions so that it’s easier to work with.
when when when you know using those expressions and that’s the way that we always approach this when when teaching it right like you you could just easily like toss this up and say like we’re gonna I’m gonna walk you through these rules because those rules are really important and I I feel like I’ve done that in my old self my first 10 years of teaching I probably did that or you probably my next iteration was like you know what there’s there’s patterning that’s happening here let’s multiply a bunch of threes together and
let’s multiply then another bunch of threes together and then say we’re multiplying these two groups of threes together and then see what the students can say. We’ll write the answer as a power and it’s like, can we see the patterning between how many threes here and how many threes here and then write the rule after that, which is like a worksheet. Can you do that? What do you see as a total? Can you generalize? That was probably my next iteration. But then to get at the power, the reasoning here, it’s like.
for a while there, would just put up complex expressions like three to the power of two times three, know, times two to the power of eight times three to the power of six times uh, three, two to the power of 10 times, you know, three to the power of one. And then I would divide the, and then it be like all that divided by, then another combination of powers of twos and powers of threes. And then I would just say, here’s our warmup today, guys. Give me an answer. And it would always work out to like, just like two times three or three times, you know, just like very, very easy answer. And then we do that a few times and then we’re like, what’s going on?
Yvette Lehman: So I feel like with all that said.
Jon Orr: Now I went down a rabbit hole when we were like, just want to know what the learning goal is,
Yvette Lehman: Well, this is what makes this work interesting and challenging, right? And I think that’s why we’re doing this episode because it’s not… This work is critical, but it’s also how do we structure it? Like if I’m the facilitator of this session where you and I are working collaboratively, what’s the goal? So are we comfortable with saying like, will understand how to apply exponent rules to simplify expressions. Like that’s ultimately what we’re working toward as our long-term objective.
Jon Orr: Yeah, like I think that’s fair to say that that is the learning goal from these two standards, but I think that for me is if I get a little bit more in a way general is that I’m simplifying, in a way you’re just simplifying expressions or calculation, like really it’s a calculation you’re simplifying and I think generally that’s an overarching theme of algebra anyway.
Right? So it’s like, what do we really like? Why? Why is this any different than collecting like terms? Well, the bigger picture is we’re trying to actually make this easier on ourselves. And those rules of algebra were developed. The shortcuts were developed to make, you know, calculations, complex compilations just easier. So we spent a lot of time trying to simplify and write equivalent expressions, because that’s another big idea that we actually haven’t used the word equivalency here.
Is that you really like this expression is equivalent to this expression and we’re and we’re showing equivalency and I think that is also really a big idea to include in the learning goal is that is that I’m we’re building in equivalence equivalent expressions and in the idea of equivalency between the different forms of You know operations numbers involve operations. What do you got?
Yvette Lehman: Okay, so do we feel good with like, I will understand equivalence in order to simplify expressions? Okay, I like that. Okay, now though, the next step I would wanna take is now I want our success criteria, which is like, what do students need to know, understand and do for this to be successful?
Jon Orr: I like it. Yes, I like those.
Yvette Lehman: Like if I want students to understand equivalence in order to simplify expressions and in this particular unit, we’re focusing on exponents. What are the skills that they need to be successful? What do they need to understand? What do they need to demonstrate? So now that we’re getting into like our I can statements. So what can I do?
Jon Orr: Right. So is this where you want to get more precise on on the actual rules, but also like like, you know, your demonstration of of your understanding on the equivalence and using the operations and equivalence? Because to me, that’s what I would be looking for. So my like my look for is, is can students can students look at an expression, use the operations to simplify into an equivalent expression, but then also reverse engineer that?
Can we look at, you know, can I build an expression that’s equivalent to this expression based off, the, using the operations that go along with making those equivalencies? Like, I wanna know back and forth, whereas I think most of the time we’re always kind of structured of like, take this, simplify it, boom, take this, simplify it, boom. And I want students to be flexible in knowing like, when is the right time to kind of use some of those operations and when not to?
and I think that would be useful. Like we would be doing that with bases that, you know, that have numerical basis. And we would also be doing that when we have algebraic basis and say both of these grade levels.
Yvette Lehman: Mm hmm. Right. So in order to construct this criteria, I feel like we would need a shared experience. Right. We actually talked about this on a call this morning. It’s like rather than jumping into the success criteria, it’s like, can we work through a problem together and talk through what did we need to know, understand and do to make this successful? So here’s our problem. We’re going to do 3 to the power of 2 multiplied by 3 to the power of negative 5.
Jon Orr: Okay, we’re just gonna do it.
Yvette Lehman: Okay, we’re gonna just, we’re gonna talk through this. Like it’s like, what do students need to know to simplify this expression?
So I’m ready. I’m ready. I’m prepared. You’re the one who’s on the fly here. I got to prep cause I’m not as confident with this, with this content as you are. So here’s one thing that I know. It’s like, I know that I can add the exponents.
Jon Orr: I know. You know that because you already know the rule though.
Yvette Lehman: Right, but well, this is what I’m struggling with. So it’s like, I know that when I’m multiplying powers with the same base, you add the exponents. but I feel like students would need expanded form to see this. So I’m going to go up to our success criteria and I’m going to write, like, I can show expanded form because it’s like without expanded form, I don’t know that we could arrive at these generalizations. Okay. I’m going to add it to our criteria. I can write an expression in expanded form. So talk us through like how would
Jon Orr: That’s exactly right. That’s how we teach it. You cannot. I love it. The other part, in this particular one, right, like you’re seeing three, you know, three to the power of two times three to the power of negative five. We also have to realize that three to the power of negative five, if you’re going to write it in expanded form, like you’re like, how do I write three to the power of negative five in expanded form? If I also don’t know the rules to kind of to be able to do some of this, right? So you also have to know that, you know, I could, I have to represent this maybe in a different
different way first, which means like, might not begin with this with my class. Like this is not, this is not the one I’m going to begin with. So I’m going to begin with like three squared divided by, you know, if not even to begin with that, I’m going to be begin with like positive exponents. But if I’m, but if I’m trying to blend the two at that time, you’re not going to go, you’re not going have a negative exponent pop up here. You’re going to be looking at, you know, dividing, dividing powers. That’s why I was saying like that, that
version where it’s like I have a bunch of expressions on the numerator. I got a bunch of expressions on a denominator. Now what we’re going to do is start to play with like what is like how do we simplify this to make this easy? if we use expanded form on the numerator, I could simplify that complex expression into maybe two powers because there’s a power of base three. There’s a power of base two. I’m referring to this this example that I was describing that I didn’t describe in full detail, you know, a few moments ago.
So that we can see that there’s, you know, there’s, can be, you know, we’re dividing these, these two and then all the going, well, how many power, like if I’m all multiplying and dividing, like I could start dividing, you know, and making ones like that was a big thing for us too, is like creating a one, like where do I see ones when multiplying and dividing and looking for ones? Like that was a, that’s a, don’t know if we want to put that in our success criteria for equivalence, because I think it’s a really important component of, you know, working and simplifying.
expressions, whether you’re working at exponent rules or algebraic rules later on and say grade 11, like a vertical stretch is like, where do I see expressions that are equivalent? And I’m dividing them or multiplying them if I’m multiplying and dividing in any order, like in a term, then if I’m divide, I can divide in any order, therefore, I can divide these two to create a one. And if I can create a one, it’s easy to work with ones and one times anything is it’s it’s the anything so that
is the part where we build towards, say, writing the expression with negative exponents. Once we see some of the relationships between the rule of, say, multiplying powers of the same base, but we also would be unpacking, well, is a negative, like, where does this negative exponent notation come from? Like, why are we writing it in negative, like, everything in negative exponent versus
a positive exponent. Like, why is it written that way? What does that even mean? So we’ve got to also unpack that, so for this to make sense, you know?
Yvette Lehman: Hmm. Well, that was like my next thing was like a negative exponent means the reciprocal. Why? Like why? Because it goes back to division. Right. So like how do so if we were going to write this as a success criteria. OK, so give me some student friendly language to articulate what we need them to know, understand or do.
Jon Orr: well, yeah. Of course. Yeah, of course. for a negative exponent.
Yvette Lehman: Well, even for like your idea of like finding opportunities to find one or helping them see division first before we move into this territory of negative exponents.
Jon Orr: Gotcha. Well, don’t know. This is always your expertise to write student-friendly language. I guess I would just say is like, can see, expressions that, or operations or expressions that will calculate, that simplify or calculate to one.
Yvette Lehman: He he. see, or find, or identify.
Jon Orr: is an important skill that I think we do. Now, this is also an important skill that I think we think is important because you’re also, by knowing that skill, you can then explain other skills. And I think a lot of folks in teachers, because I didn’t zero in on this idea of, can I simplify anywhere to a one until later in my career? It was because I impacted the ideas of it myself.
And how do I explain this to kids where we’re dividing out? Because that became a dividing out because people will say like, I’m crossing out, right? Or I’m these cancel each other. But what is canceling mean? Because that’s, that’s what’s happening when I divide three by three, right? It’s like, I cancel a three and a three, they cancel out and they go away kids think this is a magical expression that just happens. But really, why why do they cancel out because three divided by three makes a one? Where else can I make a one? And, and that’s also like,
Now I’m going to go down another rabbit hole because this is a similar property. Like making ones with multiplying to me is the same idea as the zero principle when adding. It’s like, it’s not the same, but it’s the same idea where it’s like, Hey, this, these, these fundamental truths make it easy to simplify. can divide, I can divide these numbers to make ones and one times anything is really nice. So it simplifies an expression by dividing things to make ones. If I’m adding expressions.
then I can make a zero by adding the opposite or looking for its opposite and adding them together in a complex expression. That also simplifies. These are some really nice truths that are built, some of the fundamental building blocks of simplifying expressions. So I don’t know if I’ve done any of the things that you need me to do.
Yvette Lehman: Well, yeah, no, I’m guess I wondering then if we need to be more precise in our success criteria where it’s like I can divide expressions that will simplify to one, I can add expressions to make a zero. Right? So it’s like we’re getting precise about the behaviors because that’s one of the expectations, right? It’s like the properties of the operators as well as the properties of the exponents.
So that’s where like when we’re being precise about which operator this relates to, I think it helps us clarify our criteria. So in the interest of, you know, not making this episode two hours. Yeah, maybe what we have to do is offer, you know, if anybody wants to get on a coaching call with us and actually engage in this work, please reach out. So I’m going to just recap though what we’ve done so far.
Jon Orr: Somebody’s leaning in right now going like, please do. But then someone else is leaning in going like, guys, sum this up already.
Yvette Lehman: So I think that the first step is for us to come to a common understanding of our student-friendly learning goal. We had an episode about alignment versus autonomy, and I think this is one way we can create alignment, is that if as two teachers teaching the same grade, we have a common understanding of what students are striving to around this objective. Then we need to take some time actually co-constructing a success criteria, and I think a great way to do that is by doing the math.
Jon Orr: Well, here’s I think what I think I appreciated about us doing this is that you you are acting as a skilled facilitator right now by trying to keep us on pace of going like, here’s what we actually need to develop. Because I think what we’re you know, what you’re witnessing and what I’m witnessing right now is like, how do I write that because I have a lot like where there’s a lot of knowledge floating up on teachers heads, and their understanding of the standard.
their experience teaching the standard like it’s all up here and they’re comparing that about what they have tried what they have succeeded what didn’t you know didn’t succeed what students did what students didn’t do and we’re trying to formalize that right and that’s what you’re trying to do right now is you’re trying to say like where is the where are these formal components that I’m now using my facilitation skills to bring this out so that we can have a common understanding of what is it we’re really trying to do because if we’re doing this in our PLC that
I’m spewing information about what I know about the way I’ve taught exponent rules and my understanding of them. Another teacher is going to be doing that at the same time. And we do need that person to kind of go, what are we, like, let’s make sure we’re trying to capture what it is that we feel is important about this standard. And can we get that on paper? And I think that’s that, if you’re listening right now and going, we’re all over the place, we structured this podcast episode to be like that, where,
we are coming in going, I’m just, we’re just going to talk about how we’ve taught some of these things to get before, we’re, but Yvette is here kind of trying to facilitate this process of like, if I was in a PLC, here’s what the structure is going to look like. So that we can get this out and we can kind of go, this is where we’re going to try to go. And here’s what this lesson could look like by the end.
Yvette Lehman: Yeah, I think that you mentioned like shared understanding, but also common language. So again, like students that are experiencing math education within our system are experiencing, you know, a shared vision for what this objective looks like in the depth of the curriculum, like how rigorous is it? Where are we taking this? But also the language is consistent across classrooms. So step one, we need a student friendly learning goal. Step two,
through a shared experience, want to co-construct our success criteria, which articulates really, it’s like, I will know that students are successful with this learning goal if they know, understand and can do these things. And I mean, that’s why this would probably take more than this 30 minute episode. Like this would probably take, you know, an hour, a 60 minute PLC, potentially 50 minutes, because it’s not going to be, it’s gonna be messy.
We’re going to throw out a lot of ideas, together we need to come up with this really precise language in a list.
What I would do next in this unpacking, as I would then go to our curriculum or our core resource, and I would ask myself through a backwards design approach, how are they going to assess this learning goal at the end of the unit?
Jon Orr: Good, yep, I agree. Which is part…
Yvette Lehman: or look at a state assessment or some type of summative.
Jon Orr: Yep. Yep. So it could be like your final test for the unit if you have like one or a combined one that the department uses. Yeah, I think that’s an important component. or also like, I think what many folks will do is go, what you’re saying, go look at your resource and look at what, say, some of the practice problems look like if you’re not familiar with that is because, and is that tied to the assessment? Like, are we making sure that
there’s an alignment, there’s a through line between all of these pieces. Because if my experience with my students is this, have I done, say, the necessary productive practice to make sure that I’m going to be assessing them the right way? And if not, do I modify the assessment, or do I modify my lesson? Or do I make sure there’s a nice through line between them, right? Because that’s big.
That’s a big question that I think folks have is like, could teach through problem solving. I teach through shared experience where I’m not just doing all the teaching and we’re kind of discovering some of these, shared strategies, these kind of patterns that are showing up here. but then we want to make sure that we’re moving towards like, can I simplify these expressions? Can I simplify complex expressions? Can I simplify expressions with algebraic basis? Can I simplify multiple basis? Can I, can I make sure that, you know, I have all four
You know, we’re all say three, three power rules, you know, happening at the same time. Like these are all different variations of, what you’re going to be doing and that would show up in your assessment.
Yvette Lehman: think the reason that it’s important to go to the summative is twofold. And you kind of mentioned that it’s like one, can it help us strengthen our understanding of the rigor of this grade level expectation? So maybe we’re going to use it to refine our success criteria to make sure that we are aware of what the end goal is so that every move we make is helping position our students to be successful with demonstrating their learning at the end, but also keeping in mind that our resource is not the curriculum.
So like I know here in Ontario, I think that the percentages like it has to cover 80 % of the curriculum. And it’s also based on the interpretation of the person who wrote the resource at that time. So I think it’s also reminding ourselves that we are responsible for teaching our standards. In Ontario, we teach our curriculum expectations. The resource is a guide, but it’s also, you
We can’t trust it necessarily 100%, which is why we have to develop curriculum mastery, which is why coming together and having these conversations, doing the math together, looking at our state assessments or standardized assessments in the province if we have access to them at that grade level to kind of merge our understanding, the curriculum supports or the standard supports, as well as the textbook or resource that you have as your core resource. Okay, so.
And again, keeping in mind that let’s say this is a 60 minute PLC, what’s realistic? Okay, so we’ve identified a learning goal. We’ve done some math together and we’ve talked about the success criteria. We’ve looked at a summative assessment to say, okay, well, how is this going to be assessed at the end of this learning journey? My final recommendation for this first meeting would be to pick a diagnostic assessment to take back tomorrow.
So it’s basically like, if we know that this is where students need to be by the end of this unit, by the end of this cycle, the first bit of information we wanna gather is where are they now? So can we as a team come up with a common task, right?
Jon Orr: And what do you do with that data once you have it, right? Like, if you give your diagnostic, you know, what are you now going to do with it once you know it? Is it going to change anything? Is it going to influence what you do next? it going to say, or not? Because if it’s not, why are you doing it? Right? Like, is it just to gauge, like, growth? Because you want to use the growth in the assessment when it’s time to do, say, small group or say,
you individual practice time, like if you’re going to use it somehow, then go ahead and do it. But that’s important kind of question to make sure that you kind of see where kids now, because it could influence your decision about your lesson tomorrow. You know, like you could be doing it and going like, actually, I’m seeing this, this and this. And now we’re going to structure my lesson to be like that because I can value what’s happening with kids already.
Yvette Lehman: think it’s also helpful for our next time that we come together because we know how powerful the formative assessment cycle is. And so if when it comes to unpacking standards, we’re also bringing student thinking and student work to the table because really the work is not, I mean, I want to say this clearly. It’s like, yes, we’re teaching the standards, we’re teaching the expectations, but we’re also teaching students. And it’s like, our goal is to take every individual student
and provide the appropriate experiences for them to be successful at the end of this learning cycle or by the end of the semester around this objective. so bringing the student learning to the table to do that co-moderation, we talked about in other episodes, like how important co-moderating assessment is. I think it’s worthwhile when it comes to unpacking a standard is that we figure out where they need to go.
We have a common understanding of what the outcome is going to be, but then we work together to target our instruction to be really responsive to the learners in our classroom. And we leverage our grade level partners to know what the next moves are. You like to help inform the instructional moves along the way.
Jon Orr: Yvette mentioned, you know, those other episodes, were episodes, if you’re keeping count, or if your podcast platform is sharing what episode numbers are, then those episodes are 361 and 362, two back to back episodes where we unpacked the structure of the PLC that we’re talking about, and it’s a multi-day structure. And what does that look like over time? So we’re talking about like the beginnings of that structure, because coming back is like, let’s look at the data, let’s plan a lesson together, like we can be doing that work as well. We didn’t talk about like,
the planning of the lesson or using the curriculum or modifying it to get at say the high quality vision of instruction that you want to be happening in your classrooms. Like these are components as well. So 361, 362 in those episodes in there we’ve shared kind of a framework for how to structure those days. You can get on over there and download that so that you can see what those days would look like on paper at a high level. Yvette, anything else to wrap up here today?
Yvette Lehman: I’m curious, reach out if you have a protocol that you use to unpack a standard. Like I hear people say this all the time. They’re like, we’re going to unpack the standards. But I actually am not, like I said, completely sure what that means. Like this is my interpretation and our interpretation at this time of what it means to unpack a standard. Also given the constraints of staying within like a 50, 60 minute teacher collaboration period.
But I’m curious what else is happening out there and what districts are doing that have been successful because ultimately the goal we’re trying to achieve here is curriculum mastery and strengthening teacher content knowledge. And so that’s where it’s like digging in, doing the math together, talking through and articulating and generalizing through the co-construction of learning rules and success criteria is a heavy lift, but also really important work.
Jon Orr: sure, for sure. And so if you zoom out, if you think about like what we’re talking about here about this, say, very specific use of your PLC time to do what he just just said is if you zoom out a layer, like this PLC time, we you know, it lives in say, the bigger the bigger picture of the support you’re trying to provide educators and support as a teacher, you’re trying to, you know,
also be involved in for your teacher. you’re a coordinator, a math leader, you’re trying to think about all these pieces. So for us, we view this four-stage process and coordinating and implementing what we’re talking about here lives in stages two and three for us. So building capacity is a really important stage that we need to be focused on the content, helping our teachers build their capacity, which for us is stage three in the content-specific focus.
Stage two is about thinking about your structures. So optimizing your structures, which lives in PLC land. PLC here is like one of your structures that you want to make use of. But what we talked about here needs to be coordinated with any set of large pull-outs that you’re doing with teachers, making sure that there’s a nice continuation alignment between what’s discussed across the district at any big PD days or kickoff days. Is the PLC’s reinforcing that work?
we see that there’s a connection between that work because teachers need to see that, administrators need to feel it. Then are we now taking this a step further? So if we’re doing PLC work, say collaboratively, and we’re unpacking a standard, how are we supporting that in the classroom? Like are we in our one-on-one coaching environment? Like are we going in there talking about this particular lesson or this particular standard when we go there? Like is there a connection there? We need alignment across all three of these levels, which is kind of…
really important component of stage two and optimizing these structures and creating alignment, which also needs stage one, which is your vision for high quality instruction that needs to be aligned across the district or across your school system. So these are the components that are kind of like we talked something very specific today, but if you zoom out a layer and you zoom out a layer, it lives in this, like this land of like this well coordinated, sustainable environment for math professional development. And that’s and that was those.
Jon Orr: Those parts are really important. can get a clear picture of what that looks like or sounds like as a whole. If you head on over to makemathmoments.com forward slash discovery, makemathmoments.com forward slash discovery. can see our pieces of the four stages and also get a glimpse of what that should look like for your school or school district.
Thanks For Listening
- Book a Math Mentoring Moment
- Apply to be a Featured Interview Guest
- Leave a note in the comment section below.
- Share this show on Twitter, or Facebook.
To help out the show:
- Leave an honest review on iTunes. Your ratings and reviews really help and we read each one.
- Subscribe on iTunes, Google Play, and Spotify.
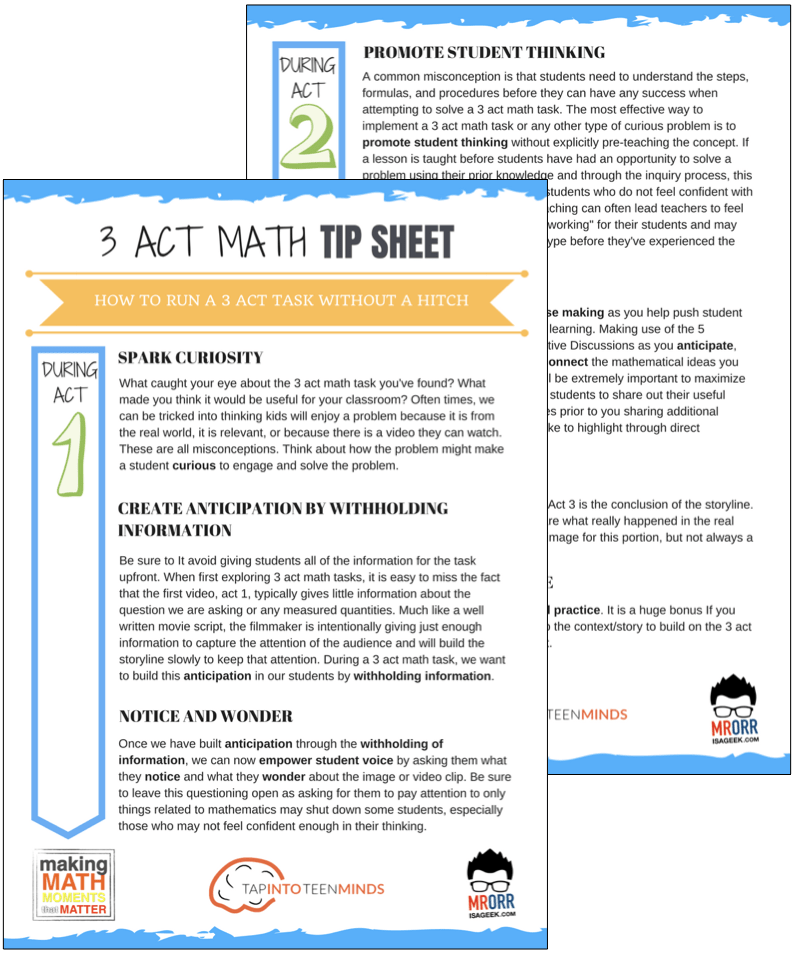
DOWNLOAD THE 3 ACT MATH TASK TIP SHEET SO THEY RUN WITHOUT A HITCH!
Download the 2-page printable 3 Act Math Tip Sheet to ensure that you have the best start to your journey using 3 Act math Tasks to spark curiosity and fuel sense making in your math classroom!
LESSONS TO MAKE MATH MOMENTS
Each lesson consists of:
Each Make Math Moments Problem Based Lesson consists of a Teacher Guide to lead you step-by-step through the planning process to ensure your lesson runs without a hitch!
Each Teacher Guide consists of:
- Intentionality of the lesson;
- A step-by-step walk through of each phase of the lesson;
- Visuals, animations, and videos unpacking big ideas, strategies, and models we intend to emerge during the lesson;
- Sample student approaches to assist in anticipating what your students might do;
- Resources and downloads including Keynote, Powerpoint, Media Files, and Teacher Guide printable PDF; and,
- Much more!
Each Make Math Moments Problem Based Lesson begins with a story, visual, video, or other method to Spark Curiosity through context.
Students will often Notice and Wonder before making an estimate to draw them in and invest in the problem.
After student voice has been heard and acknowledged, we will set students off on a Productive Struggle via a prompt related to the Spark context.
These prompts are given each lesson with the following conditions:
- No calculators are to be used; and,
- Students are to focus on how they can convince their math community that their solution is valid.
Students are left to engage in a productive struggle as the facilitator circulates to observe and engage in conversation as a means of assessing formatively.
The facilitator is instructed through the Teacher Guide on what specific strategies and models could be used to make connections and consolidate the learning from the lesson.
Often times, animations and walk through videos are provided in the Teacher Guide to assist with planning and delivering the consolidation.
A review image, video, or animation is provided as a conclusion to the task from the lesson.
While this might feel like a natural ending to the context students have been exploring, it is just the beginning as we look to leverage this context via extensions and additional lessons to dig deeper.
At the end of each lesson, consolidation prompts and/or extensions are crafted for students to purposefully practice and demonstrate their current understanding.
Facilitators are encouraged to collect these consolidation prompts as a means to engage in the assessment process and inform next moves for instruction.
In multi-day units of study, Math Talks are crafted to help build on the thinking from the previous day and build towards the next step in the developmental progression of the concept(s) we are exploring.
Each Math Talk is constructed as a string of related problems that build with intentionality to emerge specific big ideas, strategies, and mathematical models.
Make Math Moments Problem Based Lessons and Day 1 Teacher Guides are openly available for you to leverage and use with your students without becoming a Make Math Moments Academy Member.
Use our OPEN ACCESS multi-day problem based units!
Make Math Moments Problem Based Lessons and Day 1 Teacher Guides are openly available for you to leverage and use with your students without becoming a Make Math Moments Academy Member.
Partitive Division Resulting in a Fraction
Equivalence and Algebraic Substitution
Represent Categorical Data & Explore Mean
Downloadable resources including blackline masters, handouts, printable Tips Sheets, slide shows, and media files do require a Make Math Moments Academy Membership.
ONLINE WORKSHOP REGISTRATION

Pedagogically aligned for teachers of K through Grade 12 with content specific examples from Grades 3 through Grade 10.
In our self-paced, 12-week Online Workshop, you'll learn how to craft new and transform your current lessons to Spark Curiosity, Fuel Sense Making, and Ignite Your Teacher Moves to promote resilient problem solvers.










0 Comments