Episode #405: How To Teach Multi-Digit Multiplication
LISTEN NOW HERE…
WATCH NOW…
In this episode, we explore why multi-digit multiplication continues to be the thorn in so many teachers’ sides. We talk about why sometimes we need to step back in order to step forward—focusing on place value, composing and decomposing numbers, and building connections between strategies.
We highlight the differences between invented strategies and the standard algorithm, and share classroom-tested approaches that support both fluency and conceptual understanding.
Whether you’re teaching upper elementary or middle school, this episode will give you strategies to strengthen multiplication foundations and help students move from procedures to true mathematical reasoning.
Listeners will hear:
- Why 2-digit and 3-digit multiplication is a persistent challenge for many learners
- How composing and decomposing numbers helps build stronger multiplication strategies
- The role of arrays and area models in connecting visual reasoning to symbolic notation
- The value of invented strategies alongside the standard algorithm
- How to balance fluency with conceptual understanding in multiplication instruction
Attention District Math Leaders:
Not sure what matters most when designing math improvement plans? Take this assessment and get a free customized report: https://makemathmoments.com/grow/
Ready to design your math improvement plan with guidance, support and using structure? Learn how to follow our 4 stage process. https://growyourmathprogram.com
Looking to supplement your curriculum with problem based lessons and units? Make Math Moments Problem Based Lessons & Units
Be Our Next Podcast Guest!
Join as an Interview Guest or on a Mentoring Moment Call

Apply to be a Featured Interview Guest
Book a Mentoring Moment Coaching Call
Are You an Official Math Moment Maker?

FULL TRANSCRIPT
Yvette Lehman: We put out an email recently to our community asking them about our upcoming training sessions. So once a month, typically we offer training sessions in the evening here in Ontario, so 7 p.m. Eastern time. And really the purpose is just to build capacity with our community to come together and do some math and really focus on content. And so I’ve been receiving these emails from all of our listeners and members of our Academy.
And we’ve had an overwhelming response for one particular topic that really, I think it surprised me. Maybe once, I was surprised by the number of people who, was like email after email, I kept opening them and it was like the same response, the same response. And then I’d get a random other topic.
Jon Orr: Is this surprising? I was just gonna say, is it surprising this topic is the…
Kyle Pearce: You know what though, like I now I’ve seen the emails, I know the topic, but I’m not maybe that surprised. I think it’s like maybe surprising to us or maybe surprising to you, Yvette, because we’ve we’ve focused on it so much over the last five, six years. And I think, I don’t know, I think sometimes you feel like the quote unquote, we did that happens. And unfortunately, we haven’t.
quite done that, or at least we haven’t quite implemented. Every time, and we’ve talked about this in some of our leader episodes where we talk about when we do professional development, we often in our minds sort of like check it off the list. It’s like we covered that. We did it, just like we do in class. When we cover a topic, we think it’s good and let’s move on. But the reality is that we actually need a whole lot more time.
Jon Orr: What do mean by that? Tell me more about we did that.
Kyle Pearce: and attention in order to actually feel comfortable, confident with it. And then only then can we as educators then put it in place in our classroom. So I think there’s a lot of people that have seen some things around this topic, but may not have felt confident enough to maybe actually implement some change in the classroom.
Jon Orr: Got it. I’m sure people are like trying to guess right now. Like what is that topic? Yvette, hit us.
Yvette Lehman: Yeah, it was overwhelmingly multiplication, but in particular, two digit and three digit multiplication. So I’m thinking.
Jon Orr: yes. how do I make that relevant? How do I do that differently? You know, that’s a stickler in my mind.
Yvette Lehman: Our fifth and sixth grade teachers. Yes. Like I know the audience. It’s our fifth and sixth grade. Typically this is, it kind of dominates that curriculum or those standards at those grade levels. And it’s a hurdle for a lot of students and probably a lot of teachers. I mean, I was there. Certainly I taught sixth grade for many years. And when you just feel like they’re just not getting it and maybe the resource that you have, isn’t positioning them to be super successful with this particular concept.
Jon Orr: Got it. what do you, now Kyle, I know Kyle you’ve had a ton of experience as well, like diving into this topic for sure. And I’m gonna show my ignorance a little bit here because I, primarily high school teacher, lowest I ever taught was the seventh grade. So while I can predict where some of the hangups for kids are, where they would be in say two digit and three digit multiplication, give me what you’re thinking. What is it like?
Is it just the repetitive nature of trying to teach kids an algorithm that is like, I don’t remember how to put a zero here or carry this. And it’s like, or is there something else that’s really like hanging people up here?
Kyle Pearce: I honestly think the way we learned multiplication was very rote when it was single digits or maybe up to 12 times 12. And then after that, it was all algorithm and a very specific algorithm if you’re here in North America. And I think it just robbed us in our own learning experience to actually understand what’s going on. Why does this algorithm even really work?
If you’ve never really thought about it, you probably just do it and you know it works, you trust it works, and therefore, it must be the simplest way to teach other students just like us, because it worked for us. Look at us, we’re teaching kids now. So it must have worked, and therefore, it must be the best way. But in reality, it’s so critical, in my opinion, and I know we bet you’d agree with this, that we understand not only how it works, but also developing
a trajectory towards an algorithm and like allowing that algorithm to emerge so students can come at it, especially if you get hung up because we know the students who struggle the most tend to get hung up somewhere along the lines. And if you lose your place in an algorithm without any sort of understanding or any way to sort of back map and sort of like take some steps backwards to go like, where am I, you know, get back to that place of trust. We’re in really, really
big trouble. And I think our fifth and sixth grade teachers are going, I want to do something else, but like, I’m not confident. And then secondly, do I even have the time to do this? You know, like, how long is this going to take? So let’s dig into this thing. And like, let’s chat a little bit about what does this look like and sound like? And, you know, how do we help some of these educators who are listening going, I want to do more of this. I want to do well, but at the same time, I also have to be realistic about like, you know,
How long is this gonna take? What does it look like? Is it all in one lesson, one week, one month, or throughout the entire school year?
Yvette Lehman: I went back to van der Waals work because I wanted to just kind of brush up on my understanding of ways to introduce multiplication, particular multi-digit. And without oversimplifying, and I don’t want to rob people of the understanding that comes from this chapter, but he essentially talked about scenarios that lend themselves to what he called invented strategies, which is what we would call like flexible strategies.
You know, and he basically goes to say like, students need more than one method because you want them to be flexible depending on the relationship between the quantities. And so there are a lot of friendlier, let’s say, you two digit and three digit facts that we don’t need to even touch the standard algorithm. But then he does go on to say later in the chapter.
But there are some facts. And the example he gave was 486 multiplied by 372, where he would say the standard algorithm is the most efficient strategy when the numbers become less friendly. So I almost wanted to talk through both scenarios. What do we do or how would we support students in building understanding when they’re working with facts that are maybe a little bit friendlier and lend themselves to invented or flexible strategies?
And then let’s talk about, you know, when is it time to actually use the standard algorithm because it’s the most efficient because the numbers are pretty ugly to work with. So I’m going to throw 27 multiplied by 40 out to the two of you. And I want you, and I mean, I know you’re on the spot right now. I didn’t prep you at all, but let’s just talk through it. If we wanted to use an invented strategy or a flexible strategy to work through 27 multiplied by 40, what are you thinking?
Jon Orr: Kyle, you wanna go first? Well, want me to go first?
Kyle Pearce: Well, I was going to say, for me, the strategy that I feel most comfortable and confident with is partial products. It blew my mind when I finally was exposed to the partial product strategy, especially visually, breaking numbers down, chunking numbers up, and then essentially creating sums that we could put together. So that would be.
where I would resort to, but I’m like, I’m looking at this number and I’m going like, maybe there’s a better way. Like I like trying to think outside the box a little bit and I go, know, like 27 times 40, when I look at that number, 27 times 40, like 27 is close to 30 and that’s sort of, okay, sorry, I thought maybe you were gonna go partial products, but you know, like I look and I go, well, like 30 times 40 is like really close, but then,
Jon Orr: Restore my strategy. Keep going, keep going. No, did, in a way.
Kyle Pearce: right away, I definitely know that students and myself included would go, hmm, am I flexible enough to go like backwards and like, you know, and and move down because I think 100 % like, that’s where I would want to definitely draw this out and sort of make the 30 by 40 and then like, try to figure out where am I going to have to take away because I think sometimes they sort of get they go like, do I have to take away like 327?
Jon Orr: Right. How often do you see kids do that, right?
Kyle Pearce: Do have to take away three 40s? Do I have to take three of some other number? Like that’s where things get a little tricky with that type of strategy. But I think the more we can expose students to these types of strategies and doing this in like number talks and such at the beginning of a lesson can be really helpful to almost, you know, create the opportunity for them to apply it. But then also I like to say sometimes force them because I think until we actually
have them try some of these strategies, like it’s just gonna be an idea that they’re not feeling confident to actually put into place.
Yvette Lehman: Yeah. So you described basically, you know, a partial products over subtraction scenario, which I agree. Like maybe if this was 29, that would be super obvious. Like typically when the number is close to a 10, we want to, you know, like overestimate and then compensate. What I did with this one is I thought about, I really like 25 times four. So I decomposed 27 into 25 and two.
And then I did like a four times 25 is a hundred, two times four is eight. That’s a hundred and eight. And I just need it to be 10 times greater. So it’s 1,080 because 40 is 10 times greater than four. So what I actually did is on the left, I decomposed in an additive way. I was like 25 plus two. But then on with the second factor, I factored it and I was like four times 10 so that I could then just multiply by 10.
It doesn’t really matter. What matters is if it’s efficient for you, right? Like we’re talking about flexibility and efficiency. And I think that what Vandewald describes is like, we want students to have these different strategies in their pocket. And a lot of them rely on decomposing and composing number, but we need a lot of opportunity to live in these strategies.
Kyle Pearce: Well, and one thing I want to make sure we don’t like gloss over here. I did not hear you say like take the zero and place it over here for a bit or anything like that. Like you were very clear that you actually factored the 40. And I think for us trying to get clear in our own minds as to what I’m actually doing when I decompose numbers, when I factor numbers, like these are very important for us to understand, maybe not for the student yet, but
why it needs to be clear for us is so that we can model that and we can help them better understand what’s going on. Because if we start using tricks or like what appears to be magic for a lot of students where like we take a zero and put it over here and then we’ll bring it back in later, like if there is not a clear understanding for them, they will start taking digits and doing random things with them at certain times because they think, you know, the magic will sort of, you know, take over. So I really think it’s
critical that when we’re using some of these strategies that we do it, we do the work ourselves, but then we also try to think of like, how are we going to articulate to students what happened here? And then also, how do I articulate to a student what they did? Because sometimes they’ll be flexible with the numbers, but they can’t describe it themselves. That communication takes time. And I think that’s a really important piece here because
If we start getting flexible, but we’re not clear on why or how, and a student asks a question, that’s where things get a little bit muddy really fast. And I think that’s where sometimes we might shut down and go like, I don’t know. I don’t know if this is the right move for me. And we just have to be comfortable that that’s going to happen sometimes. But let’s make it a goal of ours to try to be very clear as to why what we’re doing makes sense so that our students can understand and apply those things as well.
Jon Orr: Right, like I think what you’re describing here and I would have bet it was alluding to is that we need to create opportunities where students use their flexible strategies, use their own thinking to try to solve this problem. But then also like I think what we need as teachers is what does that look like? Like does that look like it’s a free for all in the classroom? How does the consolidation look? is everyone trying something different in groups? Like talk, maybe share some of the insight here.
If a teacher was like, okay, it sounds like what you’re saying is I need to give kids more upfront, maybe friendly numbers to experiment and work with these types of flexible strategies on their own, but then it’s like, do I lead them to this algorithm anyway? Like how does the lesson end? Like what am I really trying to do here from a perspective of like where we’re trying to go in terms of the learning goal with students?
Yvette Lehman: So I think that I will be clear that with 27 multiplied by 40, I probably wouldn’t lead them to the algorithm. I don’t think the algorithm is the most efficient strategy when you’re working with numbers that are friendly. I think that what you’re saying though is like we’re not just gonna throw 27 multiplied by 40 out and allow any type of strategy efficient or inefficient and not create some scaffolding so that students are starting to own.
new, more efficient strategies. And that’s where I think, and we’ve talked about this all the time, like carefully crafted problem strings are a really great way to do this work because you are facilitating the conversation. You’re listening for particular strategies to emerge, then you’re modeling them on the board. You’re being explicit. might be incurred. Okay, this student just shared this strategy where they factored. Let’s look at another one. This is another one where, you know, you have a multiple of 10.
Can we use that same factoring strategy with this next problem? Now you go and practice it and try it on your own. So you’re definitely creating this scaffolded opportunity where you as the facilitator have the learning objective in mind. So like if I want students to see that they can factor 40 into four times 10, or any multiple of 10 or 100 can be factored and then we can multiply it by 10 at the end, I’m gonna select
particular problems in the string where that strategy makes sense. And I’m going to facilitate learning to get us there by the end of the lesson, by the end of the math talk.
Jon Orr: Yeah, yeah, and we said like that, the thinking that you just described there is like, you think about it in terms of like when you flip the page to say like tomorrow I’m gonna do two digit by two digit multiplication, that’s nowhere to be found. You know, like that’s not in the book that says like, structure it this way, you make sure that you scaffold it this way. the learning goal actually isn’t.
to just multiply any two-digit by two-digit numbers. Actually, the learning goal here today was for us to decompose these numbers this way or to think about factoring this number this way. And that’s the kind of pathway I want you to go down because our goal spread across a number of lessons, likely, is that we’re trying to build flexibility in terms of strategies that says, and almost like give kids permission, it’s okay to solve problems or multiply in
different ways and that’s the goal is actually to understand and unpack how can we multiply in different ways so that you feel comfortable with that strategy or this strategy or this model or say this algorithm when we say unpack the algorithm itself. Like I think there’s a lot there in that statement that you kind of said.
Kyle Pearce: Well, oh, no, that’s okay. I was going to just hop in and say, you know, like the one thing I love so much about different number strings and such. So for example, Kathy Fosno’s work, know a lot of the work that we’ve done at math moments have taken similar paths to get there is like that 27 times 40 instead of just randomly starting there. The string might be like, you know, it might actually be 25 times four to start and then it might be 25 times 40.
Yvette Lehman: Well, and then you did. Sorry, go ahead, Kyle. Then I’ll jump in.
Kyle Pearce: And then it might be 26 times 40. Then it might be 27 times 40. And then there might just be a random one that’s a couple moves away but follows the same pattern so that we can really be explicit for students, almost like it backmaps what you’re doing, but right from the start, from the thing we knew, the thing that felt obvious, and then making small adjustments to kind of increase that flexibility. And I think that
That is so critical for us that when we give 27 times 40, you did it to us, but I think you knew we had a little bit of background here where we could play with some of these. And you can do that with your students at some point. But when we’re trying to introduce some of these moves, we want to make sure that we give them low hanging fruit at the beginning, and we inch our way or inch further from that low hanging fruit so that they can then go, you know what? When I do see something that isn’t as familiar, I can kind of work my way back and get there.
Yvette Lehman: So you mentioned the standard algorithm and there’s such a debate right now. Like I see it all the time in social media, but like whether we need the algorithm or not, I always like to say, I think we live somewhere in the middle of that debate. And so van de Waal did also explicitly state in the chapter, know,
there are situations where that is the most efficient because decomposing it is going to become so complex that, you know, it’s going to be hard to hang on to and, and all these things. So the example he gave us 486 multiplied by 372. And I think the problem that a lot of our grade, you know, five and six teachers face is that’s the problem that will be in the book on day one. The first, like it’s like in these textbooks or resources that I’ve used at this grade level in the past, it’s like they,
interpret the grade level expectation at grade level without any scaffolding leading up to it and with very unfriendly numbers. so teachers are almost, they feel like I have to just jump to the algorithm. So what we would argue is, you know, go back, work with one digit by two digit, two digit by two digit, one digit by three digit, take the time, work with friendly numbers, build up students flexibility and understanding because the reality is,
they’re not going to encounter these really unfriendly three digit by three digit often in the real world where they can’t use a calculator. So like to spend time, you know, banging your head against the wall with these facts and these facts only that are super unfriendly, I don’t know is the best use of time, but does that mean that we never teach it? I don’t think that’s true either. Like I do think that there is an opportunity for us to build understanding of the standard algorithm.
as another tool for their toolkit when the numbers are unfriendly and reasoning through it is gonna be too labor-some. But what we often see in textbooks is they jump right to the steps and they jump right to memorizing the steps without the conceptual understanding. And Kyle, that’s where I did a ton of learning with you and from you around the use of the array model and how powerful that tool is as a starting point for the standard algorithm.
even a concrete array. And the example that Vandewaal gives actually is like starting with the concept of area. So like use area of a rectangle, know, create a context, like a garden and the garden is 46 meters by 12 meters. And we’re trying to figure out the square meters of that garden. So it’s very concrete. And then basically it’s like, we are going to learn the steps, but the steps built on the visual and built on the conceptual understanding versus just expecting that they’re going to memorize and be able to put the zero in the right place or shift the digits without any understanding of why they’re doing it.
Kyle Pearce: There’s a huge bonus too with like really giving you an opportunity to talk about units of measure, which we did a lot of work together on as well, Yvette, in terms of, you know, how often are there scenarios where kids come up with a number, but then there’s no units or they don’t know what the units are. Is it centimeters? Is a centimeter squared? Is it centimeters cubed? Like instead of just having these rules that like area is always squared and volume is always cubed and
you know, all of these things, you can actually make sense of it. And it makes it obvious to students. So when we do play in that area model, you literally can count these like squares, you know, and like students can really get familiar with like, there’s a reason why we’re doing this. And it’s not just some random rule. And you start to see students making more and more sense, not just around multiplication.
but around measurement and they start to understand other parts and they start to see math as that connected subject that we say it is, but that a lot of students never actually experience themselves. for me with the standard algorithm, if someone said you could only teach one strategy for students to be flexible with, it would be partial products because it does.
connects so nicely to the standard algorithm. Now, that is not me suggesting you should only focus on one, but I’m saying if there was only one, like that one is going to have a huge amount of value, especially since whether we agree or not that the standard algorithm should be taught or shouldn’t be taught, the reality is as many curriculum, it is there. And therefore, if you are going to be doing the things that you’re supposed to be doing as a math educator,
Like that’s going to be a huge, huge model. So it’s a great place to start. If let’s say you’re going like, listen, I’ve always just taught the algorithm. I know that it’s not helping all students. Where do I begin? Like that I would say is a great place to start. It’s not the only place. It’s not the place to end, but you’re going to see some quick wins in my opinion. When you get more flexible with it and you help your students to become more flexible with it, because you’re going to start, they’re going to start to go, my gosh.
this is the exact same thing, which it really is just following a very specific way to partition or to decompose the digits.
Jon Orr: Okay, I’m gonna unpack the elephant in the room here just for sec because everyone who’s listening, either they’re supporting teachers or they are, you you are a teacher and you’re thinking about this and you’re thinking, okay, like I’ve typically been jumping in this way where I’m supporting a teacher who’s always just kind of gone by the book or gone by the resource that they have and it does start with 486 by 372 so I have no choice but to teach the algorithm. The timing, talk to me about the timing. Talk to me about time itself because I think the elephant is like, well,
How do I stretch this across my little is it all typical time? How do I how do I make this work if I if I’m dedicated to helping kids develop flexible strategies starting with you know easy numbers flexible numbers working on those strategies giving them practice time on those strategies introducing the model that actually like makes sense if it is the area model and then and then using that area model with those strategies and then all of sudden ending with the algorithm eventually because it is like you said you’re not going to not teach it so
Where did, like, because everyone’s like, that’s a lot of time. Like, is that a year’s worth of time? Like, where does this fit in? Like, help address, like, what are the sort of creative approaches you guys have taken?
Yvette Lehman: Do you see me set up for this? I really excited. I was actually reviewing a curriculum that a district was looking to adopt recently. And right away, I was really scared because I noticed that the unit on multiplication and division was in May in the pacing guide for fifth grade. And like, even just looking…
Jon Orr: I saw you. I knew you were… I knew you were with me.
Kyle Pearce: There will only be adding and subtracting from now until then.
Yvette Lehman: Well, and it’s like, of course they’re doing other strands and those strands are going to integrate multiplication division, but the actual explicit instruction on multiplication and division where they’re likely tackling three digit by three digit was, you know, three weeks in May. And I was really scared, even if a teacher just looked at the pacing guide at a high level view, that the story that that would tell is that we’re not multiplying and dividing until May. And I truly believe that multiplication division are a year long concept.
and it cannot be limited to a three week cycle or a four week cycle. It’s like this has to live and breathe within your, and that’s, think that’s maybe why we’ve struggled with it to be honest. It’s like we treat it as a unit, but that’s never going to be enough time. Unless we’re really explicit, right? Like we’re really looking at the multiplication and division that exists.
Jon Orr: Exactly. Okay, I’m glad you said this. So you’re fitting it in, right? You’re fitting it in here, you’re fitting it in here. It might be the beginning of this warmup or this warmup. Maybe you have a small group over here. You have this activity that’s running. It’s an all year thing. And by the end of the year, you’ve covered all of these pieces and you’ve broken it up. you’re talking about space practice. You’re talking about space learning versus mass practice, mass learning. And I think I’m so glad you said it because in a way as a high school teacher, that’s exactly how I treated algebra at
say the ninth grade, the 10th grade, when we introduced say, you know, expanding, factoring, all of that, it was a semester long tackle. So that wasn’t, we weren’t waiting until the quadratics unit before we got into that. We were multiplying strategically with different ways all the way through, just like you’re suggesting. You’re gonna approach two digit and three digit multiplication.
Yvette Lehman: If anybody wants to join us when we tackle multiplication, that’s going to be our topic for October. So typically it’s on a Tuesday, Wednesday in October. If you aren’t receiving that communication, reach out to us and we’ll share the link with you. And this month is going to be addition and subtraction. That was the second most popular topic that came in from the request from the community. So we’re going to start with addition and subtraction in September and then in October, we’re going to focus on multiplication. We’re going to model some of the strategies that we described here today.
Jon Orr: Awesome. You can find all of our, all of these events, all these trainings over at makemathmoments.com for slash training. If that’s where you’re gonna find, say, the subtraction webinar, you can register right now for that if you’re listening to this in live time, when it airs. Every month we’re gonna put a new one up. So you can always go back there to that link and see what’s coming up or see what’s available for you to register to. Also, we’re also gonna put.
the replays up there too. So if you miss it, and you can always see also what we did last year. We had a year’s worth of trainings up there now to go back and have a peek in. Like last year, September, I think, what’d we do? We did division. Yeah.
Kyle Pearce: My friends, hopefully, hopefully this has been helpful for you. Head on over to makemathmoments.com forward slash trainings if you’d like to check those out. And we’re looking forward to digging into some more of these popular topics here as the new school year emerges.
Thanks For Listening
- Book a Math Mentoring Moment
- Apply to be a Featured Interview Guest
- Leave a note in the comment section below.
- Share this show on Twitter, or Facebook.
To help out the show:
- Leave an honest review on iTunes. Your ratings and reviews really help and we read each one.
- Subscribe on iTunes, Google Play, and Spotify.
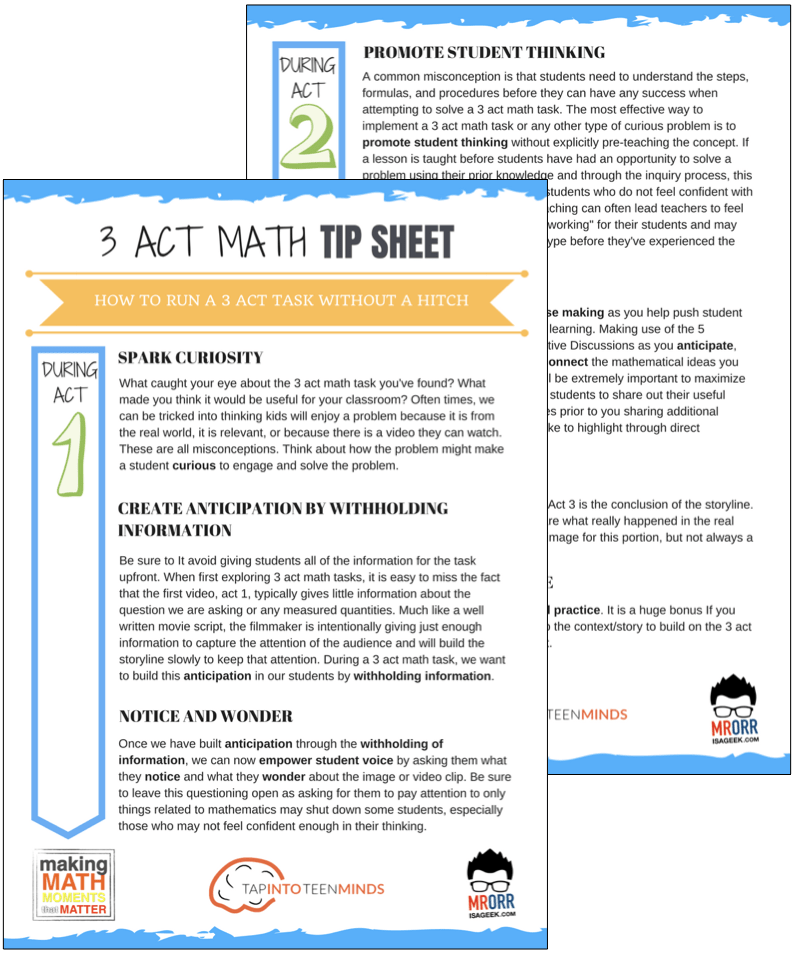
DOWNLOAD THE 3 ACT MATH TASK TIP SHEET SO THEY RUN WITHOUT A HITCH!
Download the 2-page printable 3 Act Math Tip Sheet to ensure that you have the best start to your journey using 3 Act math Tasks to spark curiosity and fuel sense making in your math classroom!
LESSONS TO MAKE MATH MOMENTS
Each lesson consists of:
Each Make Math Moments Problem Based Lesson consists of a Teacher Guide to lead you step-by-step through the planning process to ensure your lesson runs without a hitch!
Each Teacher Guide consists of:
- Intentionality of the lesson;
- A step-by-step walk through of each phase of the lesson;
- Visuals, animations, and videos unpacking big ideas, strategies, and models we intend to emerge during the lesson;
- Sample student approaches to assist in anticipating what your students might do;
- Resources and downloads including Keynote, Powerpoint, Media Files, and Teacher Guide printable PDF; and,
- Much more!
Each Make Math Moments Problem Based Lesson begins with a story, visual, video, or other method to Spark Curiosity through context.
Students will often Notice and Wonder before making an estimate to draw them in and invest in the problem.
After student voice has been heard and acknowledged, we will set students off on a Productive Struggle via a prompt related to the Spark context.
These prompts are given each lesson with the following conditions:
- No calculators are to be used; and,
- Students are to focus on how they can convince their math community that their solution is valid.
Students are left to engage in a productive struggle as the facilitator circulates to observe and engage in conversation as a means of assessing formatively.
The facilitator is instructed through the Teacher Guide on what specific strategies and models could be used to make connections and consolidate the learning from the lesson.
Often times, animations and walk through videos are provided in the Teacher Guide to assist with planning and delivering the consolidation.
A review image, video, or animation is provided as a conclusion to the task from the lesson.
While this might feel like a natural ending to the context students have been exploring, it is just the beginning as we look to leverage this context via extensions and additional lessons to dig deeper.
At the end of each lesson, consolidation prompts and/or extensions are crafted for students to purposefully practice and demonstrate their current understanding.
Facilitators are encouraged to collect these consolidation prompts as a means to engage in the assessment process and inform next moves for instruction.
In multi-day units of study, Math Talks are crafted to help build on the thinking from the previous day and build towards the next step in the developmental progression of the concept(s) we are exploring.
Each Math Talk is constructed as a string of related problems that build with intentionality to emerge specific big ideas, strategies, and mathematical models.
Make Math Moments Problem Based Lessons and Day 1 Teacher Guides are openly available for you to leverage and use with your students without becoming a Make Math Moments Academy Member.
Use our OPEN ACCESS multi-day problem based units!
Make Math Moments Problem Based Lessons and Day 1 Teacher Guides are openly available for you to leverage and use with your students without becoming a Make Math Moments Academy Member.
Partitive Division Resulting in a Fraction
Equivalence and Algebraic Substitution
Represent Categorical Data & Explore Mean
Downloadable resources including blackline masters, handouts, printable Tips Sheets, slide shows, and media files do require a Make Math Moments Academy Membership.
ONLINE WORKSHOP REGISTRATION

Pedagogically aligned for teachers of K through Grade 12 with content specific examples from Grades 3 through Grade 10.
In our self-paced, 12-week Online Workshop, you'll learn how to craft new and transform your current lessons to Spark Curiosity, Fuel Sense Making, and Ignite Your Teacher Moves to promote resilient problem solvers.










0 Comments