Episode #413: When Tools Steal Thinking: Rethinking Technology Use in Math
LISTEN NOW HERE…
WATCH NOW…
In this episode, we dig into the tricky question every math teacher faces: When is a calculator a helpful tool—and when does it actually rob students of valuable mathematical thinking?
Yvette shares a personal story about a conversation with her son on whether he should use a calculator for an upcoming test. The discussion quickly expanded: is a lower score worth it if it means students are pushing their math brains harder? Jon and Kyle weigh in on the role of calculators and AI in classrooms—acknowledging that sometimes these tools provide necessary accommodations, but other times they shortcut the very cognitive work that builds fluency, number sense, and problem-solving stamina.
Together, we unpack:
- The difference between appropriate accommodations and missed opportunities.
- Why productive struggle and mental math strengthen students’ “math muscles.”
- How to help students and families navigate the balance between tools and thinking.
- Parallels between calculators and AI—when they accelerate learning, and when they rob students of meaningful connections.
This is not a call to ban calculators—but a reminder that timing, context, and intention matter.
Attention District Math Leaders:
Not sure what matters most when designing math improvement plans? Take this assessment and get a free customized report: https://makemathmoments.com/grow/
Ready to design your math improvement plan with guidance, support and using structure? Learn how to follow our 4 stage process. https://growyourmathprogram.com
Looking to supplement your curriculum with problem based lessons and units? Make Math Moments Problem Based Lessons & Units
Be Our Next Podcast Guest!
Join as an Interview Guest or on a Mentoring Moment Call

Apply to be a Featured Interview Guest
Book a Mentoring Moment Coaching Call
Are You an Official Math Moment Maker?

FULL TRANSCRIPT
Jon Orr: In this episode, we are going to go on the way back machine here just for a moment. It’s been a while since we have had a math mentoring moment episode, which is a episode structure we’ve used for many years, which is where we interview a teacher, an educator just like you, and together we brainstorm pebbles in their shoes and ways to overcome them. Now, our guest today.
is a voice you’ve heard familiar, know, we’ve been familiar if you’ve been listening for the last year and a half or so. Yvette Lehman is our mentoring, mentee, mentee. So Yvette has brought us a question here to, that she is, know, is the pebble rallying around in her shoe right now? Kyle and I are here. We are going to unpack the pebble with Yvette. And again, together we’re gonna brainstorm some strategies. to make Yvette feel a little bit more comfortable here. Yvette, welcome to the show. Let’s get into it.
Yvette Lehman: Thank you. It’s nice to be a guest today. You know, I just, I’m a guest. Yes. Said I’m going going to monopolize this time for you to help me work through my pebble. So last night, yeah.
Kyle Pearce: Yeah, getting vulnerable, getting vulnerable.
Jon Orr: All right, let’s do it.
Kyle Pearce: I’m super excited because we have no clue what this is. So I want to make sure everybody. Yeah. A surprise for us, a surprise for everyone. So it’s a true mentoring moment episode. So, I’m, leaning in here.
Yvette Lehman: Okay, so here’s the context. Last night I saw on my son Leto, he’s in sixth grade, I saw on his class homework board that they have a quiz coming up this Thursday. And I know he’s been working on multiples factors, prime and composite numbers. We’ve been working on them all week. We throw out a number, we talk about what we know about that number, what we know for sure it can be factored by, what we know for sure it can’t.
And so of course, you know, being the good mom that I am, I’m like, leto, how are you feeling about this quiz? You know, are we feeling good? Are we feeling ready? Do we need to do any practice? And he says to me, it’s all good. I can use a calculator.
Jon Orr: So, you’re smiling though, so it’s okay. So you’re laughing. So, see, if you’ve listened to Yvette on the show for the last year, you know that this is gonna trigger her. join us in asking Yvette, like, what is it about this comment that has got you so riled up?
Kyle Pearce: Okay, okay, so that is, it’s triggered you, I can tell it’s triggered you a little bit.
Yvette Lehman: gosh. Yeah. I’m triggered. Yes. Well, I’m glad I didn’t say much at the time. I needed to think about it. But of course, you don’t woke me up at 5 a.m. this morning, which is why we’re here. I couldn’t shake it.
And the reason that it bothered me, I guess, or it’s something that I need to figure out, like that’s why we’re here, right? To think about what my best move is in this situation is because I feel like him practicing for this quiz this week, doing his reps, and then writing the assessment using a calculator is just such a missed opportunity for him because I know that he is capable.
Like I know he can use his reasoning skills. He can use what he knows about the properties of numbers and he doesn’t need to guess and check and punch things into his calculator. And it got me thinking about calculators as an accommodation in the classroom. And sometimes, you know, I’ve taught sixth grade, I understand it’s like, we know that a calculator might be an appropriate accommodation for one. And so we make it available for all. But for him,
Like I want him getting a workout for his neural pathways. I want him digging into this all week long and revealing the divisibility rules and drawing conclusions about when we know it’s not for sure divisible by eight.
Jon Orr: I, so here’s what I, I’m just gonna, I’m gonna throw back maybe an interpretation of what I think you’re really after here is that, you know, while the quiz is trying to assess his understanding of probably factors and multiples and whether he can probably produce some factors and produce some multiples, you’re actually saying, I would rather this learning goal on this quiz be more about the mental workout that he’s gonna get.
than actually demonstrate his understanding of, like you’re putting more of a priority on the actual cognitive workout he’s gonna get by removing the calculator than just the assessment of whether he knows this or doesn’t know it. Is that an accurate statement for you today?
Yvette Lehman: exactly our conversation. So I did approach him this morning after being up since 5am about this. Pretty much.
Jon Orr: Did you go wake him up? Like you were like, Leto, I’ve been, you could imagine that it’s like, she’s sitting in the dark in the living room. He comes down and flips the light on and there she is. Just like scares the crap right out of him. And she’s been, I’ve been up at 5 a.m. I’ve been worried about this comment.
Kyle Pearce: It’s like, mom, mom, why are the batteries stolen from my calculator? I’ve been thinking about you. Yes.
Yvette Lehman: Yes, exactly. This is what happened. I tried not to go at him right away. Like I let him wake up a little bit and then I was like, so let’s talk about preparation for this quiz and when you write this quiz. And I said, you I don’t think you need to use a calculator. And I said, and frankly, I think it’s going to rob you of
some really good thinking this week and some like really good reps and some really good, you you can uncover some of these divisibility rules that are, as we know, Kyle, like we’ve talked about the divisibility rules. They’re hard to teach if you’re just teaching them as rules. You really have to emerge them because you recognize patterns in numbers. So I was like, you know, I just think you don’t really need a calculator. And I said, I just, I think you’re going to miss the opportunity for some really good thinking. And I described it like a workout.
I was like, you are working out your neural pathways when you engage in mathematics with your brain. And I said to him, like, I know your brain is capable of this work. And so I just don’t want you relying on that tool because I don’t think you need it.
Kyle Pearce: I think your approach is honestly, it’s fantastic because the reality in my head as you were describing this scenario is like, I immediately want to go back to the teacher. And you think about the teacher. And as you had mentioned, I think you articulated it so well. The teacher is wanting to make sure that, OK, I’m focusing on this specific concept. And they want to make sure that all students have
access to that concept, which makes perfect sense. And then of course, on your end, you’re going like, but that, you know, that can be taken the wrong way. And the messaging you gave to Leto, I think is the messaging that you in a way want to share with all the students. But then at the same time, now how do you do that in a way that’s not going to be isolating to a student who needs that calculator, you know, really relies on that calculator. So I just want to, I guess,
speak to all the teachers out there who are grappling with this type of situation and recognize that this is really hard situation to be in. And in some ways, part of me is going, do I try to encourage certain students to try it without a calculator first? At what point do we actually encourage? So for example, let’s
you’re able to use this calculator. Like at what point does it make sense for you to now maybe go, OK, I tried it. I put in some good effort here. I’ve given myself a bit of a workout. But I’m kind of stuck on this one. It’s almost like ongoing training to help students recognize the why behind the work that we’re doing in the first place. Because I’m going to be honest, I’ve never used a divisibility rule in my everyday math.
and therefore like I would argue the reason why they’re worth looking at. Yeah, yeah, yeah. You know what I look at and I say I I want I want kids to have what I think you want, which is the goal for introducing a lot of these concepts is so that they can build their brain so that they can become more, you know, flexible fluid and flexible. So how
Jon Orr: Oh baby, we’re gonna get in a fight now. Yeah, we’re gonna get in a fight now.
Yvette Lehman: You pain me. I feel stabbed.
Kyle Pearce: Finding that middle ground, I think, is a really hard piece in it. In a way, it makes me think how as educators can we share that same messaging that you shared with Leto, but to the greater group of students, right? So that all students are along this journey going, I have a calculator. I can use this calculator if and when it makes sense to. However, I want to try to push myself as far as I can get to without just sort of like, you know,
throwing up my arms and just grabbing the calculator because it’s fastest. You know, I can get through this activity as quickly as possible by just grabbing the tool that’s going to make it as easy for me as possible.
Yvette Lehman: one of the things Leto said to me. So he said, some of them are going to take me a long time and or I might make a mistake if I don’t have the calculator and so then we had a conversation about effort versus result and I said to him you know I’d rather you get a B on this test and it be demanding and put you in a productive struggle where there’s high cognitive demand then you get perfect and it was low cognitive demand super you know not a lot of thinking because you were just
punching and plugging. So the, you made a really good point. So I think my next move, and I asked Leto if this was okay. I was like, is it would it be okay if I contact your teacher so we can talk about identifying and helping you to identify what types of questions lend themselves to using it the, cause he couldn’t really articulate to me right now yet when he needs it versus when like you’re just using it as a shortcut.
Like if we’re just using it because it’s easier or it’s going to be faster, yet we have the ability, you know, we have access to the understanding to be able to use mental math to solve it. I’m like, that to me is just taking like the easy road. You just don’t want to do the work where it’s like, when are the, you know, the numbers really unfriendly or is when, when is the question really complex that, you know, it is inefficient to use a mental math strategy and you are going to rely on a tool.
Jon Orr: And, and this particular topic, it’s it’s multiples in factors. So it’s, so we’re not we’re not talking about these ugly, ugly situations where we like, look, I could, I could, I could, you know, the, the most efficient strategy is to break out the long division algorithm, you know what mean? Like, and then it’s like, because none of the other nice strategies are going to play because the numbers don’t have any relationships, or they’re not nice. Now, let me ask you this, though, like, do you see in a world like, because I think what you’re after is to say, I want
high cognitive load on my, my, my, my child or students. want students to think, do you see a place where the calculator actually allows that to happen faster, easier about a certain, like, like think about a topic. It’s like, it’s like, you know what? If I don’t use the calculator, actually the high cognitive load actually can happen.
Yvette Lehman: So I actually thought about that this morning. I actually, have the advantage of sixth grade because I’ve taught it eight times. So I told Leto, like I’ve been in sixth grade nine times, once as a student and then eight more times as a teacher. So I have lived and breathed this curriculum for eight years. Truthfully, I cannot think of a single concept unless it’s like you’re working with, you know,
let’s say surface area or volume or something, volume is not even in the grade six curriculum anymore, like where you’re working with really unfriendly decimals and the relationships are ugly and there’s a lot of steps to do. Like let’s say you’re doing surface area of something with a lot of sides and you’re trying to keep a lot of numbers and you’re multiplying decimals. Like in that case, I would be like, you know what? It’s not worth the cognitive load. Like what I want here is for you to understand spatially how to find the surface area of this.
this three dimensional shape, at this time that calculation is not the point. But truthfully, there are very few I can think of.
Jon Orr: Well, you’re bringing up a good, because I think if you’re not actively thinking about what you’re thinking about, which is like, want my students to be constantly working with numbers and thinking about number relationships and strengthening number relationships all the way through all year long, if you’re not making that the priority, then you can see that when you just grab a worksheet off Teachers Pay Teachers and you’re saying, well, today we’re just doing
division and all the division problems are, number, you can’t use, they’re unfriendly situations and then therefore you can’t strengthen that up and at the same time unpack division strategies or just unpack division in general is then therefore it’s like, well then you have to use a calculator and then that’s the situation I think a lot of teachers find themselves in. It’s like, well, how else am I supposed to, like we want them to divide, but I want them to divide
this part with the calculator or I want them to do this type of area problem but we can’t access it because the numbers are so ugly but it’s like, but you could have just chosen nicer numbers, right? You could have just like orchestrated this situation so that it was accessible to get at the higher level thinking then because I think as a high school teacher, we used to say this all the time. It’s like, I would rather let the calculator or the machines
do the work of like the minutiae, know, like we all know that, you know, like because we want to get to the calculus ideas or we want to get to like, we can’t do it because the numbers are too ugly. But I mean, like we got to always structure the numbers to be prettier. And I used to think about this when I was a teacher is like when I was in first year, second year, third year university, you weren’t allowed to calculate.
Like we couldn’t have a calculator on our exams or calculate, like you could have it during your assignment, but you weren’t allowed to bring a calculator into an exam in university. But all the numbers were nice. know, like if you did it wrong and you needed a calculator, you knew you were doing it wrong. In a way, like in high school and elementary school, it’s like we don’t structure it that way because we don’t take that time to think about what is it really we’re doing here and how can I create this so that we can get to it and use our brains
and our thinking so that we can, we don’t need that calculator. We rely in a way heavily on that calculator so that when we argue, well we have to get to the factoring, you know? In order for us to get to the factoring, we have to know multiples and factors. But I’d rather them know how to factor when to factor. So let’s bring the calculator in there, speed that up. But in a way, it’s like, well what are we really emphasizing? And how can we structure it so it is easily emphasized?
Kyle Pearce: Well, what it really, like to me, think like what, while this is a very specific scenario, I think it really, when we blow this up or we zoom out and we go, what is it that is causing us as educators to sort of allow kids to rely so heavily on the calculator, it’s fluency and flexibility in general, right? So I mean, really, if we can get to the core of the problem, which is we need to focus more time and attention from the beginning.
on fluency and flexibility with numbers and operations. I feel as though students would almost naturally be able to get sort of what you’re after here, Yvette, which is like reaching for the calculator actually is slowing me down. know, like imagine if we were in that world where we go, it’s actually because we’re picking numbers like John, had mentioned, like we’re going to be more strategic about the numbers we’re picking and about the things that we’re asking students to do. But because they have confidence with
fact fluency and their understanding of how operations behave, we might get to a place where it’s like, maybe this isn’t, you know, something that’s such a big deal. But I think we’re so far away from all students having fluency and flexibility that, you know, we rely so early on the calculator and we can make the excuses to this is the part I want to like call it and, and, you know, you know, try to get this off people’s minds. But people, see the arguments about
Siri and Alexa and like, don’t need to, you you just ask Siri and it’ll give you the answer. And it’s like, that’s such a cop out to suggest as though it’s like, you know what, let’s just like, let’s be creative and let’s not worry too much about the nuance when in reality, let’s get fluency and flexibility under our belt. And we can then use the technology when it does make sense to with things that are very complex or very difficult to calculate.
Jon Orr: I want to get you guys both take on this because I think I think the argument for AI the argument for technology to support us in our thinking is to say that some of these some of the details and it depends like this is where we have to make decisions like what are the right things to like allow technology to help us and what are the right things or the things that we don’t want technology to help us because you know Kyle we had Conrad Wolfram on the podcast last year two years ago and
you know, we’ve been, we were trying to get him on the podcast for a while because, you know, he’s, you know, he’s, you know, worked with, helped start, you know, Wolfram Alpha, which was an AI generative tool a long time ago and helped kind of, you know, solve math problems for you. And one of his arguments is to say like, well, I, the higher order thinking, to him was like, do I want my students to be able to factor?
in maybe factor. And I think he was talking about factoring trinomials or do I want them to know like when to factor? And then therefore I can tell the computer factor this for me so that I can use that factored form to solve this problem, this problem, this problem. And I knew that I needed it factored because it does this and it does this and it does this. The factors form of this expression is actually really helpful here and here and here. And I actually need to know that factored form. So his argument was like, I would rather them know
the when and not the how because the computer can solve the how faster and more efficiently and accurately than us. So why don’t we use the computer to allow us to do the higher order thinking and do more of the higher order thinking, but we have to decide on what the higher order thinking actually is. And I think that’s the, sometimes that’s the argument that gets used. I’m like, why we should be using calculators? But then it’s like we have to, like I said, like,
Right now I know Yvette is like ready to pounce because she’s saying, well, what’s higher than like number of
Kyle Pearce: Yeah, well, I was just going to say it’s like, how can you think in a higher order, like any type of higher order problem if you don’t have like first principles thinking, right? Like if you’re not able to like get all the way back to the most basic of that situation, we’re going to be in trouble. Like imagine we fast forward 30 years from now and it’s like, and we sort of go one extreme and say, let’s not worry about any of this basic stuff and let’s just do higher order thinking. And we get down the road. It’s like,
who’s gonna fix the problem when the AI machine doesn’t work? You know, like we’re gonna have to like have people that are able to do that type of work. And I think it’s like, let’s not waste time on things that we don’t need to waste time on. But I think foundational understanding of number sense and operation is probably the thing that we need to spend the most time on so that students can then be thinking more flexibly in these more higher order thinking situations. But Yvette. Where’s your head going on this one?
Yvette Lehman: Yeah, I think the example that you gave John is true once you have the foundation. Right? Like it’s like there’s like right now the goal at sixth grade is to be able to identify prime and composite and to be able to identify factors and multiples. And there’s probably some more minimal application of that understanding at this grade level. Like that is the top, right? So imagine like if that’s the…
product or the outcome or the the goal for this learning. I want for my child anyway for him to like deeply understand relationships not because once he has mastery of it that he needs to do a hundred of them. know like once he’s demonstrated that he has the ability to think through and reason through like and I guess that to me is the advantage of this type of work is the reasoning skills. Like it’s almost like you reveal
generalizations or truths or behaviors about numbers that you won’t forget because you’re not just memorizing rules, you’re actually emerging them yourself by doing the work.
Jon Orr: So let’s assume like by Friday, let’s assume the quiz is on Friday, you know, and let’s assume by Thursday night, you’re like, I know, like you’ve got this inside out, we’ve done this, you know, you’ve clearly confidently consistently can replicate, you know, this thinking anytime. Are they allowed to use a calculator the next day? Because now they’re at that point, it’s like, well, I’ve…
I’ve hit that, I’ve hit the assessment goal. I know this. now it’s kind of like I’ve built the foundation to do the factoring tool that Conrad Wolfram was saying. Now can I just ask the calculator to do it because I’m now more concerned about speed today than not?
Yvette Lehman: why I guess. Okay, so my question is, would the calculator even be faster at that point? Like if you just know, right? Like if you’re like, I can look at a number, I can look at 84 and I can right away reveal, because other, I think the calculator is like a guess and check strategy at this point, right? Like, I don’t know that it’s faster. Like I think that my expectation is that by Friday, he has automaticity.
Jon Orr: Sure, yeah, if you could look at it and know, then you’re right, it’s definitely not faster. I see. But then he won’t need it. He’s like, actually it’s worse if I grab it. Right.
Yvette Lehman: Like he can look at it. Right. Right.
Kyle Pearce: Well, well, and I think too, like, I think kind of to your point there, you’ve had, it’s like, you know, you want to look at it and it’s like, if you’re looking at it and you’re looking at it and you’re like, and maybe you try to break it down, but you’re like, you know, it’s an odd number. And I’m like, I’m not sure. And you’re stuck for a bit. That’s kind of when I think you want to have kids build in the trigger that it’s like,
Maybe I wanna now go to guess and check, cause like I kinda guessed and checked in my mind, cause that’s essentially, it’s either I either have the automaticity, I am seeing something that maybe I’m gonna be able to emerge the pattern by slowly breaking it down, or I’m like, I’m just, maybe this is a prime number, like maybe I can’t factor this, but I need to double check, like let me divide by some of these larger numbers and really see, but.
you can see how over time, yeah, like you were saying, you should be able to see and almost see the decomp or the factorization. should say it’s not decomposing, but a factorization of the number at least to the next stage. Right. And then it’s like, now I might be decomposed or, or, factoring down again, another level in the tree and so forth. But ultimately at the end of the day, I think, I think,
What we have is the majority, and this is a very bold, no data to support claim just from anecdotal, but we have probably the majority of kids that reach for the calculator before even looking at the number. And that’s the piece that I think we’re really trying to halt so that it’s a look at the number and then decide what the next step is. It’s like when my daughter asked me for help with her homework, her, her go to is dad, how do you do this? And I asked her, well,
tell me about the problem. And it takes so long for us to get to a point where she will actually read the problem and then communicate it to me. I will not go over and read it for her. And she gets very frustrated and I get very frustrated, but it’s like, we’re trying to build this place where it’s like, I want you to actually read it first because I have a sneaky suspicion. You might not be asking me yet for help, maybe later, but you need to at least look at it and do a little bit of thinking upfront. regardless of what that concept is that you’re working on.
Jon Orr: I’m thinking about the sixth grade class for a second here, and it’s like, because I think what you’re also after here is that, and I think this is where we feel like we’re landing, is that ideally you want Leto to self-assess that this is a problem I got out of the ethnicity for, it doesn’t make sense for me to grab a calculator, and I think lots of students get to that point for certain ideas, certain skills, certain topics, strands. But you also.
You also want them to be like, this is a problem I do need the calculator for, which is a self-assessment, which is one of the highest order of thinking, I think, that we can ask a student to do. So imagine you have your class now, it’s like, how do I help? What are the moves in your sixth grade class? You’re the nine year expert. What is the move to help all the sixth grade class just self-assess more? You know what I mean?
Is it, not gonna use calculators to do this task, but where’s the line and how do I help decide where that line is? And is it really just a constant reaffirming to students? Is that we don’t need it yet or you might not need it yet, let’s try without it. If we need to grab it, we’ll grab it. You know what I mean? We know that you’re constantly trying to strive towards only accessing it when you absolutely need it. And I think that’s an important skill for kids to take away, but how do we help that class do it?
Yvette Lehman: hope that that’s the outcome for us, for Leto. I, first like my gut reaction was I want to say no calculator ever. And it’s like, even if he grapples through a really complex calculation, like that to me is better. And if he’s, it’s wrong, it’s wrong. And that’s okay. But like, I’d rather him even attempt it first, you know? But I think you’re right. I need him to be able to identify. So that’s actually what I asked him. I said, bring home your review work. And I want you to show me the question that you think.
the calculator would be helpful for and why so that I can understand where and when he thinks the calculator would be appropriate and maybe he’s right, you know, so that’s something we’re going to do this week. But to your question about individual students, I guess it depends on what we value. And that’s what I was trying to explain to him is like, if we value productive struggle and like we value
sitting in that that deep thinking and hard work because that’s the outcome we want for math classroom versus like sometimes I think all of us are guilty of like there’s a lot of curriculum to cover. We need the path of least resistance with the greatest success. So we take shortcuts to get us there because we have to move on. We have to make sure we want everyone to be as successful as they possibly can. So we’re going to put this accommodation in place. We’re going to make this easier. But I guess
It depends on what we value and what we want the outcome of math class, the math classroom to be. And like for my kid, like I said, like I’d rather him take longer and not even finish the assessment or get questions wrong. If it means that every other day this week, he’s, he’s working hard. Like he has a workout for those neural pathways. He’s making connections. He’s put himself in a place where he has to have some productive struggle. There’s like this, this rigor.
And that goes back to kind of the question you asked earlier about, you know, at what point does AI get in the way of some of that just heavy work? And I think about like our own cognitive decline. Like if we are relying on AI to do things for us that we can do, we’re actually not giving our brains the same level of workout, like, you know, vocabulary retrieval, things like that, like actually digging into the research ourselves.
Having to construct my own question in response to a standard or a curriculum expectation is a lot more rigorous for me and it actually helps me deepen my understanding than asking an AI tool to do it for me. So it’s like finding that balance between efficiency because we have a lot to do and a lot to cover but not robbing ourselves of the opportunity to strengthen.
know, our cognitive abilities, and especially for our students. Like, I would hate for us to be robbing our students of the ability to, like, build their brains, you know? Like, build those connections and those pathways in their brains because we’re taking shortcuts.
Kyle Pearce: I think this really speaks to how important mindset is when it comes to education, not just mathematics and then really all things in life is like, it’s so easy for us to fall into the trap of like, we’ve just got to get this done, right? And I think as educators, we’ve just got to get the curriculum done is sort of what is going on in our minds. Instead of this curriculum is something that we can use to help grow
these kids’ brains, right? And so that they can be better and they can think, you know, more flexibly and fluently. So I think it’s really important that we as educators not only remind ourselves of that, but then also make it very explicit for kids. Because that, think, is going to be the key piece is that every time we’re coming to school, that mindset piece, it can’t be just something that we put on the wall or we set on day one, you know, that, hey, in this class, we do these things. John, you talk about your pillars.
Right? You can’t just speak to the pillars on day one, put a poster on the wall and hope that kids understand what that means. It’s like, how do we build that into everything we’re doing on a daily basis? So that routine is there so that we’re constantly reminded of why we are here. Like, why are we doing what we’re doing? And it’s not just to get it done, right? Even though that’s where I think a lot of us land over time. that
to me is maybe my big takeaway from this conversation is like, we’ve got to make sure that it’s explicit, us educators, parents, but then also very explicit to the kids as to like, what really matters here. And I think you’re doing a great job with making Leto understand what really matters when you go to do that quiz test or even just show up to math class on a daily basis.
Jon Orr: in true math mentor moment episode style. We have to ask Yvette, well, what is your big takeaway from this conversation? What’s your next move?
Yvette Lehman: think that my big takeaway is like, I want to be like all or nothing. You know, like I feel like I am so like, I just want to be like, this is it, you know, like blanket statement, like, give me your calculator. this is like, it’s the opposite of an accommodation. But I think what I heard, which was one of the ideas that was in my mind is like, I just need him to be able to be better at self assessing and like to not take the shortcut.
like in the theater are going to be questions where it’s like, you know what? You’re right. Like this isn’t worth the time or cognitive load it’s going to take. Go ahead and use a calculator. But for the other eight on the quiz, the calculator is actually going to slow you down because you have automaticity of these facts.
Kyle Pearce: Hmm. I always break it down to like exercise and fitness and things that, you know, it just feels so obvious, but it’s like, if you’re constantly taking the shortcut in a workout, you’re at hockey practice and you’re constantly not doing the drill correctly, or you’re constantly like in a way it’s like you’re robbing yourself of that improvement. And I think it’s, it’s easy to lose that site when we’re doing things like cognitively, right? Because it’s like, you’re not physically seeing
you know, the shortcut, right? It’s all up here and it’s very easy to miss. So I think it makes it even harder. But then think about as humans, like we take shortcuts all the time in areas that we really shouldn’t be doing. So, you know, kind of give yourself that permission to go, this is hard, but you know, I think if you continue down the path that you’re on, you know, you’ll have more success with at least him over time, being able to better identify. That’s why we’re doing what we’re doing.
And if he can build that into his math learning, think of all the other aspects of his life that he’ll be able to apply the same thing. I know he’s going out for the play, you know, and he wants a lead role. It’s like, Hey, are you going to take the shortcut on trying to get those lines down? Are you going to, you know, put in real effort when you take 20, 30 minutes a day to, you know, to practice those lines or to practice that dance move that, you know, we know he loves doing as well. So I like this discussion.
Jon Orr: We want to hear from you as well. What’s your take on the calculator use in your classroom? Reach out to us at our email. If you’re on our email list, hit reply in any emails you get from us. We send at least one each week. If you’re not on our email list, then head on over to makemathmoments.com for us to report. There’s an assessment there you can fill out. It helps kind of identify some of the key areas of a strong math class.
fill that out, you will also be added to our newsletter, the weekly email that we send out, and then you can respond to us to let us know what is your take on the calculators in the classroom. Thanks everybody for joining us, and again, thanks Yvette for being our mentee today.
Thanks For Listening
- Book a Math Mentoring Moment
- Apply to be a Featured Interview Guest
- Leave a note in the comment section below.
- Share this show on Twitter, or Facebook.
To help out the show:
- Leave an honest review on iTunes. Your ratings and reviews really help and we read each one.
- Subscribe on iTunes, Google Play, and Spotify.
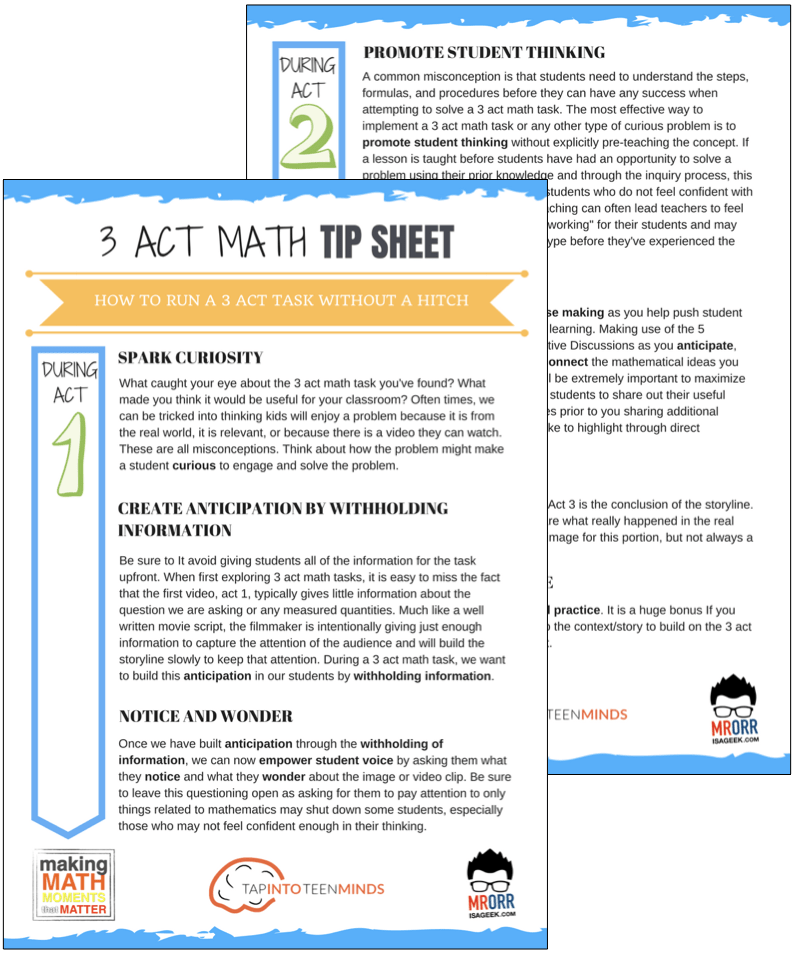
DOWNLOAD THE 3 ACT MATH TASK TIP SHEET SO THEY RUN WITHOUT A HITCH!
Download the 2-page printable 3 Act Math Tip Sheet to ensure that you have the best start to your journey using 3 Act math Tasks to spark curiosity and fuel sense making in your math classroom!
LESSONS TO MAKE MATH MOMENTS
Each lesson consists of:
Each Make Math Moments Problem Based Lesson consists of a Teacher Guide to lead you step-by-step through the planning process to ensure your lesson runs without a hitch!
Each Teacher Guide consists of:
- Intentionality of the lesson;
- A step-by-step walk through of each phase of the lesson;
- Visuals, animations, and videos unpacking big ideas, strategies, and models we intend to emerge during the lesson;
- Sample student approaches to assist in anticipating what your students might do;
- Resources and downloads including Keynote, Powerpoint, Media Files, and Teacher Guide printable PDF; and,
- Much more!
Each Make Math Moments Problem Based Lesson begins with a story, visual, video, or other method to Spark Curiosity through context.
Students will often Notice and Wonder before making an estimate to draw them in and invest in the problem.
After student voice has been heard and acknowledged, we will set students off on a Productive Struggle via a prompt related to the Spark context.
These prompts are given each lesson with the following conditions:
- No calculators are to be used; and,
- Students are to focus on how they can convince their math community that their solution is valid.
Students are left to engage in a productive struggle as the facilitator circulates to observe and engage in conversation as a means of assessing formatively.
The facilitator is instructed through the Teacher Guide on what specific strategies and models could be used to make connections and consolidate the learning from the lesson.
Often times, animations and walk through videos are provided in the Teacher Guide to assist with planning and delivering the consolidation.
A review image, video, or animation is provided as a conclusion to the task from the lesson.
While this might feel like a natural ending to the context students have been exploring, it is just the beginning as we look to leverage this context via extensions and additional lessons to dig deeper.
At the end of each lesson, consolidation prompts and/or extensions are crafted for students to purposefully practice and demonstrate their current understanding.
Facilitators are encouraged to collect these consolidation prompts as a means to engage in the assessment process and inform next moves for instruction.
In multi-day units of study, Math Talks are crafted to help build on the thinking from the previous day and build towards the next step in the developmental progression of the concept(s) we are exploring.
Each Math Talk is constructed as a string of related problems that build with intentionality to emerge specific big ideas, strategies, and mathematical models.
Make Math Moments Problem Based Lessons and Day 1 Teacher Guides are openly available for you to leverage and use with your students without becoming a Make Math Moments Academy Member.
Use our OPEN ACCESS multi-day problem based units!
Make Math Moments Problem Based Lessons and Day 1 Teacher Guides are openly available for you to leverage and use with your students without becoming a Make Math Moments Academy Member.
Partitive Division Resulting in a Fraction
Equivalence and Algebraic Substitution
Represent Categorical Data & Explore Mean
Downloadable resources including blackline masters, handouts, printable Tips Sheets, slide shows, and media files do require a Make Math Moments Academy Membership.
ONLINE WORKSHOP REGISTRATION

Pedagogically aligned for teachers of K through Grade 12 with content specific examples from Grades 3 through Grade 10.
In our self-paced, 12-week Online Workshop, you'll learn how to craft new and transform your current lessons to Spark Curiosity, Fuel Sense Making, and Ignite Your Teacher Moves to promote resilient problem solvers.










0 Comments