Episode #418: Math Fluency in Action: Observing What Proficient Students Actually Do
LISTEN NOW HERE…
WATCH NOW…
What does it really mean to be fluent in math—and are we measuring the right things in our classrooms?
Math fluency is often reduced to speed drills and memorization—but true fluency goes much deeper. In this episode, we unpack the key differences between fact fluency, computational fluency, and procedural fluency—and why it matters for both teaching and learning. Drawing on research from Jennifer Bay-Williams and John San Giovanni, we explore what fluency actually looks like in action, and how educators can spot it beyond just correct answers. Whether you’re a teacher, coach, or leader, this conversation will challenge you to rethink how fluency is developed, observed, and supported.
You’ll walk away with:
- A clear understanding of the three types of fluency and how they’re interconnected
- Observable indicators that a student is truly fluent—not just fast
- Insight into how to shift classroom practice away from rote performance and toward meaningful fluency development
Press play to rethink fluency and gain practical insight for monitoring its development across your schools or district.
Attention District Math Leaders:
Not sure what matters most when designing math improvement plans? Take this assessment and get a free customized report: https://makemathmoments.com/grow/
Ready to design your math improvement plan with guidance, support and using structure? Learn how to follow our 4 stage process. https://growyourmathprogram.com
Looking to supplement your curriculum with problem based lessons and units? Make Math Moments Problem Based Lessons & Units
Be Our Next Podcast Guest!
Join as an Interview Guest or on a Mentoring Moment Call

Apply to be a Featured Interview Guest
Book a Mentoring Moment Coaching Call
Are You an Official Math Moment Maker?
FULL TRANSCRIPT
Yvette Lehman: One of the topics that we unpack often with the districts that we support is fluency. feel like it is a big topic right now, probably paralleling the work that’s happening in literacy around just to focus on foundational skills right now. I don’t think anybody, whether, know, whatever side of the debate you’re on, nobody thinks that students shouldn’t be fluent. Like that to me is universally understood that of course, you know, we want students to be fluent and flexible. But I was asked a question the other day that got me pondering and I wanted to bring it to our conversation today. We often hear different terms when it comes to fluency, right? We hear procedural fluency, we hear computational fluency, we hear fact fluency. And the question that I was pondering is what’s the difference?
Jon Orr: Right. Right. And then someone’s like, is there a difference?
Kyle Pearce: Hmm. That’s interesting. Yeah, well, and I would, I mean, when you say certain things like fact fluency versus procedural fluency, to me, what pops in my mind right away is those are actually different, but is it the process that’s different or is it the thing that you’re actually fluent with different? So for example, you know, when we talk a lot, John, you and I for many years had been talking about how we taught very procedural. Right? So we, we memorize steps and procedures. And when I think about that, that’s very different than say fact fluency where fact fluency, I’m looking at that as something where we’re talking about, you know, probably more of those basic facts, multiplication tables, some of the division facts that you want kids to sort of know, and even addition and subtraction that we want students to sort of know with automaticity. So I mean, I look at those two and I see those as very clearly different, but as you kind of lay out all of these other scenarios and the ways, the way we describe some of these things, think oftentimes we believe they’re interchangeable and sometimes that can cause some confusion as to how we might go about them. So I’m really excited to dig in.
Jon Orr: Yes. Well, well, I think like the way that you’ve I think just tried to clarify, you know, procedure like fact what fact fluency to you was and thinking about like these facts, but then there’s procedures, which is a I think you were saying we taught procedurally, but it’s like so I’m leaning towards like being fluent procedures, but I completely agree that that someone and most teachers are saying that’s all they’re all the same like like we’re talking fluency. So that to me that means like what popped into my mind was automaticity. It’s like I just know it and that’s and that’s what I really after. I just want kids to know it and it’s like that’s fluency. So then therefore it’s like well what’s the difference between all three of these is fact fluency automaticity is procedural fluency automaticity around procedures is you know like there’s there’s these kind of terms and I think and then here’s the other question is like do we need to know what all three really mean. Like what do we need to know that? Like you know there’s teachers asking that, you know? Isn’t it all the same? John, Kyle, Like is it worth our time here? Okay, let’s dig in. Yvette, you’re up. Like let’s first maybe unpack the differences here between all three with some smarter minds other than us.
Kyle Pearce: At least as we know them or as we believe them to be now, right? We’re again, reserving the right to learn and change our thinking down the road.
Jon Orr: Right, right, I like that. Right, loosely held.
Yvette Lehman: Well, I went to figuring out fluency from Jennifer Bay Williams and John Zangiovanni to do some relearning. I’ve read the book more than once, but it’s like I need to go back to it over and over again to make sure that I deeply understand. So I think that the way that they describe the difference is the scope. OK, and they show it in almost like they’re nested. So they’re interconnected because they live within each other. But it’s like there’s almost like the scope. It’s larger and larger. So let’s start at the bottom. So Kyle, you described fact fluency as like basic facts, automaticity, and they describe it very similarly and they say it’s facts with single digits. So it could be like a double digit by a single digit, but whenever there’s a single digit involved in the computation, that would be a basic fact. So even eight times 10, nine times 12, like these are basic facts, computation involving a single digit. And I think that to your point, these are facts that ideally are automatized. They require no steps.
Jon Orr: Right? Now they might not, so here’s the worry part, right? Is that, it’s like, wait, those are facts, therefore we should just fact drill them in. And not actually work on the other two pieces to actually help them become fact-focusing. So help me understand this, is like, because they’re intertwined, is there like, I feel like there’s this like, Task-going flowing model here that like goes like hey this flows into this yeah flywheel. It’s like when I build this I get more of this
Kyle Pearce: Yeah, it’s a flywheel, John. Yeah, you like to talk about the flywheel.
Yvette Lehman: Well, let’s describe the other two terms first. So fact fluency is, know, automaticity and not memorization, but automaticity of basic facts. Next is computational fluency, which is a larger scope because it’s basically fluency with all four operators with a variety of numbers, right? So it could be double digit, three digit, decimals, fractions. Like now we’re talking about operating with all four operators. And this is where we really start to see you know, strat strategies, like because these aren’t straightforward computations, they’re not, I can’t necessarily automatize all of them. I’m going to need to rely on my strategies in order to be efficient. Procedural fluency brings in all of the other procedures beyond just computation. So it’s finding the area of a triangle, it’s solving a proportion, it’s geometric properties, like it’s more. Right.
Jon Orr: Completing the square.
Kyle Pearce: It’s like a recipe to do stuff. Yeah.
Yvette Lehman: It’s more complex than computation alone.
Jon Orr: Got it. I the recipe idea Kyle that helps me kind of like think about the difference it’s like if I need a recipe my my step-by-step algorithm and That’s the that’s a difference between like just multiplying two digit by two digit because to me it’s like well there’s a procedure to multiply two digit by two digit, but what you’re saying is that is more computational fluency to know those steps versus the more complex procedures like recipes to solve problems or to find values out.
Kyle Pearce: Right. And even that computation piece. And I like the nesting. Like, I’ve got that visual in my mind right now. Hopefully people are listening to this and kind of envisioning where this is, is, you know, if you want to be computationally fluent, you’re going to need those basic facts, right? And otherwise you’re pulling a calculator out to try to, you know, utilize what you know about computation, right? So they all kind of build off of each other. And I think that’s going to be really important here. And I, I’m still picturing this as a bit iterative as well, right? Because we can do all of this work very early on at an appropriate stage, right? So certain students in kindergarten or grade one, when we’re trying to develop their procedural fluency, we want them to be able to apply some of the facts they know, some of the computational skills that they have and the fluency there, and be able to use it to come out with you know that finished recipe right.
Jon Orr: Yeah. Yeah. Like I’m imagining like, because when I think about procedural fluency specifically, and as a high school teacher for 20 years, and I think a lot of my early years were like, I was probably viewing like, I, I’m not here to teach fact fluency. I’m not here to teach computational fluency. I’m here to teach really, like my job was like, but I never said this out loud, because I never thought about it this way, right? But I was like, I was teaching procedures. And that was what I was highlighting every day. It’s today we’re going to learn about how to find the slope of the line. And here’s the process on how to find the slope of the line. Let’s now go through that example, example, example, practice, practice. Let’s, let’s take note. Like I was, I was probably thinking mathematics to me is teaching procedural fluency so that we could have the procedures down so that when I see the scenario, I can apply the procedures to solve the problem. But I was always like, I’m not gonna like, fractions are gonna show up in this question here. Just get your calculators out because that’ll speed up the process so that we can better accumulate or better attain the procedure. Because that is the be all end all here and not say understanding computational fluency or back fluency because that’s where I put the the value and I think we all, when we think about what math class is and we’re hearing about our classrooms and say traditional teaching, I’m using air quotes here, I think this is where I think a lot of us think is like procedural fluency is just, is that’s what we’re really doing here in class.
Kyle Pearce: Well, well, and John, how many how often when we were trying to again, find the slope of the line where we’re doing some pretty basic right? So basic facts that we want students to know, like, you know, two was nine and why why one was six and kids are getting out a calculator. And that would see when I think of these tiers, go, well, that’s basic facts that that students struggling with yet. We’re trying to get them to understand a recipe for something much more complex. And I can totally relate to what you described. It’s almost like, you know, going back to our recipe analogy here that we were creating like line cooks that would just follow a process, maybe not know why they’re doing what they’re doing, but they would, you know, we wanted them to be able to like get the food down the line instead of chefs, right? Like we actually want students to be able to like think on their feet and be able to utilize some of these things and know, hey, when It doesn’t taste right. Like, what am I going to have to do to make this better? And I think the three layers here are the three levels of fluency that we’re describing, I think are all essential in order for that to happen versus someone sitting there sort of going like, now what? Like, now what do you want me to cook? Now what do you want me to do? Right?
Jon Orr: Right. Yeah. Yvette, let’s answer this question. What does it look like when a student is fluent?
Yvette Lehman: think this is a question that a lot of our districts are trying to answer because we’re trying to monitor how we will know when we’ve increased fluency across the district or across the school, across the system for both teachers and students. And so in order to monitor the impact of our action steps that we take, we need to know what the observable behaviors are so that we can notice and name them when we see them. And so again, I look to figuring out fluency and they’ve identified some actions, these observable behaviors that when a student is truly fluent or a teacher is fluent, you might see some of these things. So the first one is they select an appropriate strategy. And so the example that they shared in the book was 419 minus 297. Treating this as, and if there’s no context, of course, and they’re just working through the computation and it’s like, do they have computational fluency? If you have computational fluency for this particular subtraction scenario, you’re likely not thinking about it as removal subtraction. You know, it just, it’s like, it really, because 297 is so close to 300, it’s like, I could just shift this up and I could just see the difference between 422 and 300, like just like selecting an appropriate strategy because I know that when I have a number that’s close to a whole so whether that’s a 10, 100, a 1 if you’re working with decimals so I’d be looking for students to use an appropriate strategy but again like appropriate for me it might be different than appropriate for you depending on the strategy that you’re most efficient with but
Jon Orr: Yeah, so like you’re saying, like that’s an element of, like if I’m working with a student, or let’s say I’m working with an educator and we’re solving that problem and they select an appropriate strategy, am I demonstrating that I have stronger computational fluency over someone else? am I, like you’re saying, because like earlier you said strategies live at the computational fluency level and not procedural fluency, so am I? Am I after one versus the other or am I just trying to witness where they are? Because I think if we have to answer, when have we got better on fluency? Where’s the better lie?
Yvette Lehman: I guess I’m going to tell you when I would know that a student doesn’t have this behaviour. Imagine they were working through a variety of subtraction problems and they use the same strategy every time.
Kyle Pearce: Right. And here’s the interesting part too. I was gonna throw this in there. It doesn’t necessarily mean like my head went to, okay, so if a student uses the same strategy, maybe they’re procedurally fluent. In reality, they’re not even procedurally fluent. They know a procedure. And that doesn’t necessarily mean that they are fluent with the procedures that could be utilized for that specific scenario. So this is one of those scenarios where it’s hard first going all the way back to John, were saying like, does it matter? Like, does it matter that we know the difference? And I think as we’re digging in here, we’re starting to recognize that we really, we do need to know the difference because we need to know what we’re looking for. And most often, I think what’s going to be most helpful is when they’re not showing those signs, it could be hard. they use great strategy here or a great strategy there. doesn’t necessarily mean they’re fully fluent. but it’s definitely showing some signs that they may be, which is I think what makes this work so difficult because is there a finish line? And I’m going to argue there isn’t. It’s just continually trying to get more and more comfortable and fluent.
Jon Orr: So Kyle, because you said something interesting there about like, they may not be procedurally fluent. So to you, are you saying like, if I can, if I’ve memorized, you know, steps in a process, and every time I get thrown a question, I got that. Like I just apply the process. Like there’s no numbers here that messes me up. Like am I procedurally fluent then?
Kyle Pearce: I would argue personally, would argue unless I can’t think of a scenario where there’s only one procedure to do a thing in mathematics, like where you’re where you know a procedure, that’s great that you’re able to follow this particular procedure. But when I think of fluency, I think of like, could you do it another way? And that part makes me wonder.
Jon Orr: You wouldn’t call me fluent. So it’s not, so I just wanna be clear for everyone listening too. So we’re not saying like, I think what you’re not saying is you’re not saying like procedural fluency doesn’t exist for like the one procedure or this procedure. It’s more all encompassing than I’m procedurally fluent with completing the square. I am procedurally fluent with the long division algorithm. Like you’re not saying that each process or each procedure we are fluent or not. more all encompassing, we’re procedurally fluent with. So then, so now I have to go back though, because what makes that different? Like, you, cause you were saying like, computational, the strategies live at computational, so how do I know, like what does it look like then, when I’m procedurally fluent versus computationally fluent? Because if I select a strategy, is that, that’s indicating that I’m computationally fluent? Okay.
Yvette Lehman: Okay, I got a scenario for you. Yeah, okay, here we go. I’m so glad you asked, I’m ready. I came ready with my example. So as a team last week with our leaders, we worked through a problem. And it was a problem of the week from the University of Waterloo, and it was an area problem, okay? So imagine, it was kind of like parks and playground a little bit, Kyle, from Kathy Fosnows unit, where you essentially have a rectangular park and different areas of the park are different types of area. So you have wooded area, you have play area, and you have open space. But of course, you know, there were different sections shaded. So wooded area, maybe there’s a triangle on the left, and then there’s a trapezoid on the right. And you’re basically trying to figure out what area of the park is wooded, what area is open, what area is play. So this is where I think I can distinguish the difference. The procedural fluency was in applying the our understanding of how to find the area of different shapes, how to find the area of rectangles and triangles and trapezoids. Like that to me was like how I was applying the procedure. It was executive functioning to solve the problem. It was a multi-step problem. It required different types of operations.
And I was procedurally fluent because I was able to navigate. It’s almost like the application phase. The computational fluency came into play when I had to, for example, add two different areas of wooded and they weren’t super friendly. I was like adding 122 plus 87 and I actually had to use a strategy to do that addition. So that was where like my computational fluency was at play. And the way that I added those two areas was maybe different from the way that I added the other two areas because the numbers were different. So I used different strategies depending on the relationships. I also used my fact fluency because sometimes I just had to multiply 6 times 10 and divide by 2 to find the area of the triangle and that was automatized. I didn’t need any steps.
Jon Orr: So I think what I’m hearing from you there is that procedural fluency was like, it’s still about selection. So you’re saying fluency, your first example there with like 419 minus 297 was like, when a student selects an appropriate strategy to solve that problem, they were exhibiting signs that they were more computationally fluent. But what I think what you’re saying is like when I have maybe a scenario, or when I have a complex situation, the ability to fluently select the procedure amongst many procedures, amongst my arsenal. You I’ve got my tool belt here and I, right, so I have a lot to choose from and now I’m more procedurally fluent because I can fluctuate and I can be fluent in choosing the right one at the right time, but also going like, I think that procedure works better than that procedure.
Kyle Pearce: Sure. Which recipe should I take out?
Yvette Lehman: great. rate. But was also beyond just computational because I had to understand the properties of the shapes within the, like I had to understand the properties of a trapezoid to be able to understand how to use the procedure for finding the area of a trapezoid where actually I chose to subtract the two triangles. But it’s like, that’s procedural fluency as defined by, it’s like, it’s bigger. The scope is bigger. It’s not just computation, it’s application of computation through our other strands.
Kyle Pearce: Right.
Jon Orr: selection. I like it.
Kyle Pearce: Well, I wanna pause here for a second because I think it can be really easy for us to miss this, but I’ll go back to your slope example, John. And when I think of the way I was teaching then all of the opportunities that students in my class were missing to develop their computational and their fact fluency, because we kind of like had the calculator there as the crutch because like we didn’t want to like derail the lesson when in reality that procedural fluency, I would argue the students that were struggling with computational fluency and fact fluency and weren’t being given the opportunity to develop those also probably struggled with the procedural fluency as well, right? Cause like you don’t have a solid foundation. You don’t have confidence in what you’re doing because you don’t see the numbers. You don’t see what’s going on. And that’s gonna make even if I’m like the best teacher at, you know, communicating step by step, what you need to do every time you see slope of a line, it’s like they still just don’t have this confidence to trust that things are gonna go well for themselves because things always seem to go wrong, right? And that I would argue is part of this foundational piece here where really those I now recognize that those procedures were actually not a whole, you know, not doing a whole lot for students in my classroom when they weren’t given the opportunity to strengthen the other two tiers or the other two layers here of fact fluency and computational fluency.
Jon Orr: Alright, what are some other look-fors you bet?
Yvette Lehman: I’ll kind of go through them quickly and then maybe we can unpack them after. So these were the ones that were identified and maybe pick some that you’re like, want to know more about and I’ll do my best. I’m going to obviously tell people, read the book though, because this is my interpretation of these actions at this time. So select.
Kyle Pearce: Sure. You’re not that fluent with the book yet is what you’re saying.
Yvette Lehman: Exactly. I’m, yeah, exactly. So selects an appropriate strategy. I said, you know, I would like to see students using different strategies depending on the relationships between the numbers. And so if a student used the same strategy every single time without looking at the relationship between the numbers or the quantities, that would tell me that they don’t have true fluency. Solves in a reasonable amount of time. This one can vary, right? So the length of time it takes for a grade four student to add fractions versus a grade seven student is going to be different. But the general idea is they don’t get stuck or bogged down. So, you know, they’re not, they’re not stuck or they’re not overwhelmed or really, it doesn’t become really demanding. They trade out or adapt a strategy when it’s not working. When they get, know, they go to apply one of their strategies and they’re like, actually, you know what, this isn’t going to help me. It’s not reasonable. I’m going to swap it for another strategy that tells you they have fluency.
This is one of my favorite ones. Another action is they can apply it to a new problem. So let’s say, for example, we’re doing addition 48 plus 56 and they use the compensation strategy to make it 50 plus 54. Can they apply that to decimals? Can they apply the strategy to new situations that are novel, but the properties remain the same? So now when they see four and eight tenths and five and six tenths, can they just make a whole and do five plus five and four tenths? They complete the steps accurately. So of course, that’s something we probably would have looked for in the past. Another one we would have looked for in the past, they get the correct answer. And I think the one that I love is they check for reasonableness, but not just at the end throughout. It’s like they’re actually asking themselves, like, this going to be efficient?
You know, if I do, if I decompose this way for my break apart to multiply strategy, is that going to be efficient or am I going to get a fact that’s actually going to be unfriendly? What’s a different way that I could decompose so that I have more automaticity with this fact? We shared one recently, remember when we were multiplying 27 times 40? And I was like, I’m going to do 25 and two because it’s like 25 is really nice, but I probably would have started with 20 and seven and then been like, actually, no, 25 is friendlier when I multiply by four, I’m going to decompose it this way instead. So it’s like checking for reasonableness, not just at the end, but throughout the process to make sure that your strategy is going to be most efficient.
Jon Orr: Hmm. Mm-hmm. Now, when I think about trying to witness this with students, it’s like, okay, so we’ve got, we’re gonna look for appropriate strategies. Can they trade that? We have to also create scenarios where we can see that type of thing if we’re looking for that type of thing. But in the work that we’re currently doing, we’re supporting schools and school districts right now in helping each teacher build their procedural fluency, computational fluency, fact fluency for the students. But I think what a lot of leaders right now, coordinators, math coaches are, you know, not necessarily just realizing, but new all along is that a lot of our teachers, and especially us, maybe we also need to strengthen that part. how many, how many, when you say like trades out and adapts a strategy, how many, when you’re working with teachers, how many are doing that on a regular basis for their when they’re multiplying themselves? Or are they just turning to the calculator, right? Like how are we doing that? Because I think that’s the crux right here is like so many schools are trying to say like we want to increase this, we want to increase fluency. We’ve got to know the difference between these three so we know what to look for. But do we also know what to look for when we’re working with adults?
Kyle Pearce: Hmm.
Yvette Lehman: I if solving a problem like the one that I described that we did with the leaders last week in a PLC or in small groups in a staff meeting might start, whether that’s, know, so imagine now we’re talking about teachers. It’s like we work through a problem collaboratively where it’s a multi-step problem. It requires the application of procedures in another strand. There’s going to be computation in there with double digit numbers. are going to be opportunities for some automatized facts as well. and we look for these observable behaviors because what I’m wondering is, imagine I did this with a student, I gave them that problem. A seventh grade student, I sat down with them and I gave them that problem and I just observed them and I talked to them as they were thinking through it. I feel like if I did that problem, I could probably get to the underlying issue. Like, is it with the procedure of finding the area? Like they don’t understand the visual relationship between you know, the rectangle and the triangle or the trapezoid. Like, so is that where we’re falling apart here? Is it in the actual computation when they got to some of the more challenging addition and subtraction, they just didn’t have a strategy without a calculator or they were using an inefficient strategy? Or when I saw them, you know, it’s like maybe they know how to find the area of a rectangle, but they couldn’t multiply the single digit numbers.
Kyle Pearce: Right.
Yvette Lehman: So it’s like, think that if we engage in a task like this as an entry point, and you talk about this all the time, like start with the task, start with the task that is a high cognitive demand and application task. And then once I’ve observed those behaviors, I might be able to diagnose like, where are we falling off? Is it that we don’t know our basic facts? Is it that we don’t have strategies for computation when the numbers become more complex? Or is it that we actually don’t understand the procedure of how to decompose and find the area.
Jon Orr: All the above.
Kyle Pearce: Yeah, well, and I was going to say, like, I’m envisioning when we’re working as a group, I put in the same group of educators as we’re trying to learn and build our content knowledge. If I had to put money on it, I’m going to say the part that we are probably needing most attention is going to be in the middle, which is that computational fluency, right? It’s like, most of us are pretty good with, you know, a good chunk of facts, and most of us are pretty good with a certain amount of procedures and maybe even where we might apply those procedures, but it’s that middle ground that I think we’re probably needing to focus our time and attention on because without us having that, we can’t provide those opportunities for students in our classroom to develop their computational fluency as well. So. This is really interesting. I’ve had some mini epiphanies here as we’re working through these three layers.
Jon Orr: Well, I think I would say all of the districts that we’re currently working with supporting and talking with on a regular basis, we talk with lots of districts and lots of schools and every single one of them will have said that fluency is a major focus. It’s an objective or it’s a major area of focus for the work that they’re trying to do. And you have to ask yourself, like, okay, even if we know the differences between the three and we know some some strategies to help students develop this, if we’re not also developing those strategies for the educators, but then having the set of like the look-fors that you talked about, Yvette, being like, do we know what we’re looking for? Because down the road, you’re gonna wanna know, did we improve fluency? If it’s one of our objectives, one of our focus zones is how do we know that we made improvements this year? Like we wanna work on it, but it’s like, do we just look at student test scores and that’s gonna tell us?
Probably not because there’s a lot of cloudiness right there from one year to the next. And especially if we know that the, what you just said, Kyle, is that probably a lot of our educators we’re working with need to strengthen their computational fluency strategies and their fluency up so that they’re better positioned to do this with their students. It’s, well, how do we know we did better there? Like, how do we know? And that’s why making that look for list, the walkthrough list. Like, what does it look like when a teacher is more fluent in the, and therefore in the classroom teaching lessons, because really those are the look-fors you’re going to want to look for, right? So it’s like, if I’m going to, if I’m going to math coach or coordinator, and I want to be able to answer that question, did we improve or get better or are we stronger as a system or as a school on fluency in these grades? When I walk through classrooms or I work with teachers, what am I looking for to know that we’ve made improvements there because I think it looks different from like I’m clearly solving problems and I’m demonstrating that I’m computationally fluent, I’m procedurally fluent or in fact fluent as a learner, but as an educator, I think there’s in a way a slightly different set of look-fors, because when you’re in the classroom, the teacher is the one not doing all the computation. But you know when you walk into a classroom whether that teacher has strong fluency across all three areas or not.
Kyle Pearce: Hmm. Well, the part that, you know, for me, I think is really important for those who are listening right now is to kind of zoom out a little bit and think about what it is that you are working on in your classroom, in your grade band, in your school, in your district. And if you think about that, you know, we always talk about trying to get clear, right? And we try to get narrow. And when you think fact fluency or just fluency in general feels pretty narrow. Right? It feels narrow. But what I think we’ve just highlighted is that it’s not narrow enough. And what we really need to identify is what specifically are we looking for? And then I also want to like rope in some others because there’s lots out there.
A lot of the districts we work with that start with problem solving, right? Or they start with, you know, building, you know, the, the skill around problem solving and think about how important these three, you know, pieces, these three pipe types of fluency, how important they are in order to be able to become a strong problem solver, right? So the question then becomes is like, is it really problem solving? Is it something else? Is it something deeper than that? And as we get deeper and deeper and as we better understand what’s really going on, we can then identify the more specific changes that we can make in order to build our own content knowledge and then be able to actually implement some of these things in our classrooms so that we’re not focusing on something that’s broad. And John, at the beginning of the episode, we said a lot of times people kind of look at it as this one thing. And the reality is, is that it’s actually not. And in most cases, I would argue there’s always deeper, like we can always go deeper. when you think you’re at the answer, There’s probably five more questions to ask to get deeper and deeper and deeper so that you can get to the real root, the real problem, the real pebble that’s in your math leader shoe.
Yvette Lehman: Speaking of pebbles, I’m going to share one that many of our districts are facing currently, and it’s similar to what we’re facing in literacy as well. It is very hard to monitor fluency without sitting one-on-one with students. And so when you’re trying to system-wide support the implementation of any type of screening tool or diagnostic or collection of student thinking or growth, This is maybe a pebble that people are experiencing is that, and I know that I’ve seen Jennifer Bay Williams speak before as well, and she talks about how we can monitor fluency and it’s like the interview style, sitting and observing students, asking them about their metacognition is always going to be the best way. And that seems to be a hurdle that some of our districts are facing is, you know, buy in that this is time well spent or finding a place for it within the classroom. But I always, know, one thing I always go back to is it like, doesn’t need to be, you know, 30 questions that kids are solving. It can be one problem and you visit every student in a week to see them work through that one problem. So you can really gather some good evidence of their thinking and identify where is the breakdown happening.
Jon Orr: Yeah, and I think it’s also hard when you don’t know what you’re looking for, right? So you have to be clear to yourself, what am I actually looking for here in this situation with this student? If I’m a leader, I’m a coordinator, what am I actually looking for when I want to answer this, you know, the question of are we more fluent as a school or a grade band or a classroom? Like, we want to be able to say, what are we looking for? And that starts with defining that look for list and then also you know, monitoring that look for list, are we getting better? Are we stronger? Usually, the teams that we’re working with are developing continuums that they can see growth on over the course of a time or timelines that they’re looking to strengthen.
And you know, these are bigger issues, because it might not necessarily be fluency or procedural fluency or computational fluency that you’re actually looking for growth in no matter what, no matter when you’re what you’re trying to improve. You have to get clear on what is it that I’m looking for to see improvement, can I define it so that I can then look for it and measure it or capture it? And this is an important process. Like this is school improvement planning process. It’s a thing that you have to be going through every single year of like, how do we define what we’re looking for? What are we looking for growth? How do I know that we’ve happened? It’s part of our four stage process and it’s the beginning. We have to get clarity there and we help teams do that.
And that’s why when we say we’re working with schools and school districts, we’re helping teams develop the clarity around what is it that they’re trying to improve and what’s the process that they can install into their school system or their operating or their districts or their classrooms so that they can see progress and get traction along the way. That’s what we’re trying to do here at Make Math Moments and the work we’re doing. So if you want us to Have a peek and talk to us about what you’re currently doing to answer those questions or what your look-for list looks like or your tools that you’re using to monitor progress. Let us know. We’ll hop on a call with you. You can book a call over at makemathmoments.com. We can be talking about what those measurements look like and you can be able to answer at the end of this year, are we making progress in strengthening fluency at our school or in our school district?
Thanks For Listening
- Book a Math Mentoring Moment
- Apply to be a Featured Interview Guest
- Leave a note in the comment section below.
- Share this show on Twitter, or Facebook.
To help out the show:
- Leave an honest review on iTunes. Your ratings and reviews really help and we read each one.
- Subscribe on iTunes, Google Play, and Spotify.
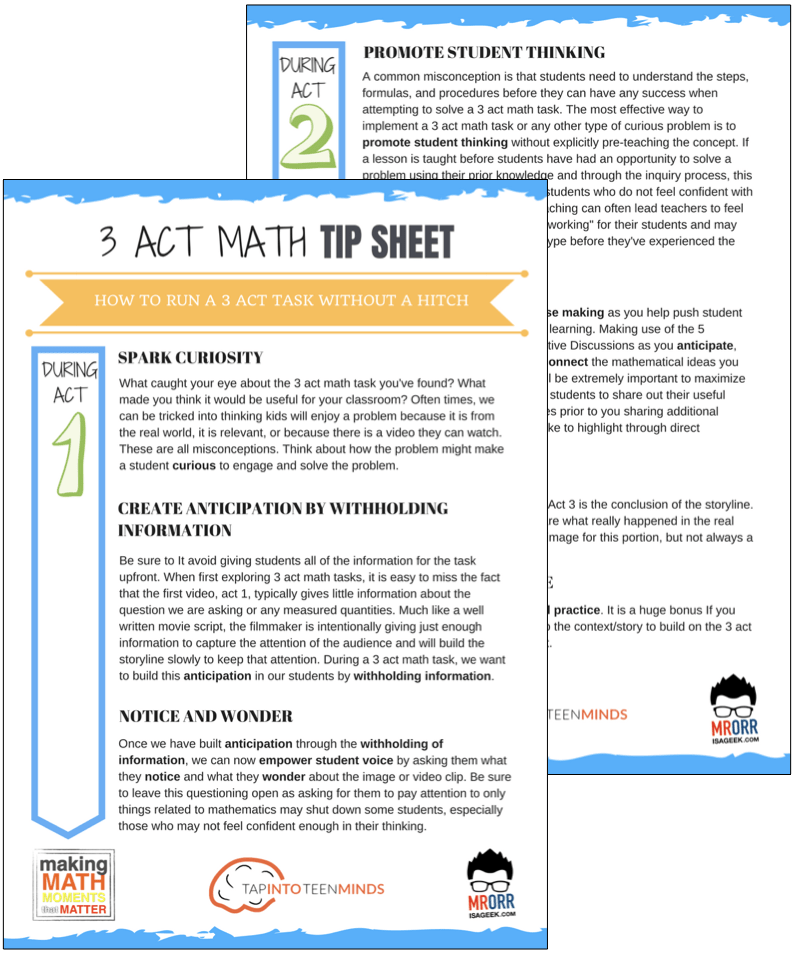
DOWNLOAD THE 3 ACT MATH TASK TIP SHEET SO THEY RUN WITHOUT A HITCH!
Download the 2-page printable 3 Act Math Tip Sheet to ensure that you have the best start to your journey using 3 Act math Tasks to spark curiosity and fuel sense making in your math classroom!
LESSONS TO MAKE MATH MOMENTS
Each lesson consists of:
Each Make Math Moments Problem Based Lesson consists of a Teacher Guide to lead you step-by-step through the planning process to ensure your lesson runs without a hitch!
Each Teacher Guide consists of:
- Intentionality of the lesson;
- A step-by-step walk through of each phase of the lesson;
- Visuals, animations, and videos unpacking big ideas, strategies, and models we intend to emerge during the lesson;
- Sample student approaches to assist in anticipating what your students might do;
- Resources and downloads including Keynote, Powerpoint, Media Files, and Teacher Guide printable PDF; and,
- Much more!
Each Make Math Moments Problem Based Lesson begins with a story, visual, video, or other method to Spark Curiosity through context.
Students will often Notice and Wonder before making an estimate to draw them in and invest in the problem.
After student voice has been heard and acknowledged, we will set students off on a Productive Struggle via a prompt related to the Spark context.
These prompts are given each lesson with the following conditions:
- No calculators are to be used; and,
- Students are to focus on how they can convince their math community that their solution is valid.
Students are left to engage in a productive struggle as the facilitator circulates to observe and engage in conversation as a means of assessing formatively.
The facilitator is instructed through the Teacher Guide on what specific strategies and models could be used to make connections and consolidate the learning from the lesson.
Often times, animations and walk through videos are provided in the Teacher Guide to assist with planning and delivering the consolidation.
A review image, video, or animation is provided as a conclusion to the task from the lesson.
While this might feel like a natural ending to the context students have been exploring, it is just the beginning as we look to leverage this context via extensions and additional lessons to dig deeper.
At the end of each lesson, consolidation prompts and/or extensions are crafted for students to purposefully practice and demonstrate their current understanding.
Facilitators are encouraged to collect these consolidation prompts as a means to engage in the assessment process and inform next moves for instruction.
In multi-day units of study, Math Talks are crafted to help build on the thinking from the previous day and build towards the next step in the developmental progression of the concept(s) we are exploring.
Each Math Talk is constructed as a string of related problems that build with intentionality to emerge specific big ideas, strategies, and mathematical models.
Make Math Moments Problem Based Lessons and Day 1 Teacher Guides are openly available for you to leverage and use with your students without becoming a Make Math Moments Academy Member.
Use our OPEN ACCESS multi-day problem based units!
Make Math Moments Problem Based Lessons and Day 1 Teacher Guides are openly available for you to leverage and use with your students without becoming a Make Math Moments Academy Member.
Partitive Division Resulting in a Fraction
Equivalence and Algebraic Substitution
Represent Categorical Data & Explore Mean
Downloadable resources including blackline masters, handouts, printable Tips Sheets, slide shows, and media files do require a Make Math Moments Academy Membership.
ONLINE WORKSHOP REGISTRATION

Pedagogically aligned for teachers of K through Grade 12 with content specific examples from Grades 3 through Grade 10.
In our self-paced, 12-week Online Workshop, you'll learn how to craft new and transform your current lessons to Spark Curiosity, Fuel Sense Making, and Ignite Your Teacher Moves to promote resilient problem solvers.










0 Comments