Episode #379: Why Your Fact Fluency Fix May Have Failed (So far) & What To Do Next
LISTEN NOW HERE…
WATCH NOW…
On a recent coaching call, we spoke with a new teacher who was feeling great about a math quiz her students had just aced—until she wasn’t. The quiz focused on using the array model for multiplication, and students were awarded points for drawing the array and getting the right product. But when we looked deeper, something didn’t sit right: Did these scores truly reflect her students’ understanding and grade-level expectations?
In this episode, we unpack what was missing from the math assessment and why simply getting the “right answer” isn’t enough. We explore the importance of strategy sophistication, the difference between additive and multiplicative thinking, and how to design math assessments that actually measure mathematical proficiency.
In this episode, you’ll discover:
- High scores don’t always mean high levels of understanding in math.
- Strategy sophistication matters—especially in assessing multiplication.
- Math assessments should reflect not just answers, but the thinking behind them.
- Teachers can refine math assessment practices to better capture student growth and proficiency.
Attention District Math Leaders:
Not sure what matters most when designing math improvement plans? Take this assessment and get a free customized report: https://makemathmoments.com/grow/
Ready to design your math improvement plan with guidance, support and using structure? Learn how to follow our 4 stage process. https://growyourmathprogram.com
Looking to supplement your curriculum with problem based lessons and units? Make Math Moments Problem Based Lessons & Units
Be Our Next Podcast Guest!
Join as an Interview Guest or on a Mentoring Moment Call

Apply to be a Featured Interview Guest
Book a Mentoring Moment Coaching Call
Are You an Official Math Moment Maker?

FULL TRANSCRIPT
Yvette Lehman: John, thinking back to your experience as an elementary student, how did you feel about multiplication tables?
Jon Orr: Hey, I think I’m on record here on this podcast of saying I was a master multiplier. Yeah, like I was my jam. And, you know, I, that was my math moment. You know, if you’ve listened, if you rewind and go back to episode one, two or three, and if you’ve listened that long, you know, this is, we’re in the three hundreds now, but if you listen that long, you’ll hear my moment. My moment has always been.
that I used to get these puffy stickers for multiplying. Like I just crunched multiplying, you know, two digit by two digit, two digit by one digit, one digit by one digit and like those elementary grades and it made me feel like super awesome. However, cause I would just pump through and I think I had like on my desk, the multiplication chart, but I could like carry the one and put this here and put a zero here, you know, like I do all of the structure, but I remember
And this is where the moment actually came from is because when my mom pulled out a long time ago, like 10 years ago, pulled out like an old test from that multiplication time, I remember like grade five, just being able to, or maybe was grade four, like just being able to do this well, pulled this test out. Even though I had all these stickers and these like workbooks, all of a sudden on the test, I it was like 18 multiplication questions. And I had done probably something
like looking at it now as a math teacher looking, had probably done the same mistake over and over over again on that one test. And, but at the very top, there was a comment from the teacher and the comment said, terrible work. It was like just harsh, terrible work. like, and I forget there was another subcommon I, terrible like work carefully or something like that, but it was just like the terrible was there.
you know? And so that was that was hilarious about that because it was like, felt like I was really good because I had all these stickers. But then it was like when push came to shove on that moment, on that day, something didn’t didn’t click for me. And I clearly wasn’t showing something either I didn’t know it because I don’t remember myself back then. Like I learned multiplication just like we all did, you know, memorize the multiplication tables, and then transfer that into just following the algorithm. So
So I could follow algorithms well, obviously, but I had missed something along the way to get a terrible comment from my teacher.
Yvette Lehman: My husband was the same as you. He actually, one of his core memories in elementary was that he always wanted to be the fastest and he still knows the name of the student, right? That he was caught, like if we see her out in public, he’ll remind me of the time that she beat his score on the multiplication quiz. Like he was really motivated to be really good at it. And he still to this day, like really felt like it worked well for him.
where I am, of course, as you know from my previous episodes, like the worst, I still don’t know my multiplication facts by memory. Like I still use strategies and I can get them pretty quickly, but I don’t have them memorized. I still don’t, I can’t memorize anything. And so we know, right, that, you know, that strategy of rote memorization is probably going to work for some and not others. And Like you described, John, it’s like even for those that it works really well for, like they have a great working memory and they’ve had enough practice to hang on to the skill. It doesn’t mean that it’s necessarily going to transfer to their ability to reason with quantities or understand the relationship between quantities.
Jon Orr: Right. For sure. Kyle, what’s your memory of multiplication in elementary school?
Kyle Pearce: you know what I think I just remember feeling actually at the time I don’t think I felt lucky. think looking back on it, I just know that I was sort of lucky, you know, because I didn’t really try a whole lot like I didn’t. It wasn’t like I was like hyper focused, but I knew them. I think my mom used to do some like flashcards with me at home because that was the expectation. So I
luckily have a fairly good memory. Like I was able to, you know, and I think a little bit, I recognize some patterns which may have just sort of happened, but again, all luck. And I don’t know how other than mimicking through like mimicking my way through school, as I’ve talked about on many episodes before.
it, I didn’t really know how to problem solve, you know, and it was like, almost like gave me the mindset of like, if I don’t already know the answer, I don’t want to even engage because it was like, I knew that I don’t remember doing that before. And I thought math was all about knowing or having experienced a specific thing in order to be able to provide any sort of value, right? And it was almost not worth engaging in. And I now recognize how wrong and incredibly wrong that is. but you know, it was something that for me, just felt like what math really was. That’s what it was defined as based on my experiences.
Yvette Lehman: So when I was a grade two teacher, it was at a time when there was a shift away from, let’s say flashcards, rote practice, memorization. I feel the message that I received at that time was that that is bad. it’s like, it’s like, it’s almost like if you got caught with a mad minutes, like you were, you were in trouble because of, and I understand why, like research tells us that
You know, as far as student confidence and self-esteem as a math learner, it can be incredibly detrimental. We know that it doesn’t yield the results we want, which is students who can reason and justify and problem solve and make connections. And that it’s really, you know, a band-aid solution that masks, you know, gaps in underlying conceptual understanding. I get that. Here’s the problem though. When everybody came in and told me, you know,
ditch the flashcards, ditch the mad minutes, ditch the multiplication tables, ditch homework because we don’t want to have kids practicing after school, they need to be kids. My issue is that I just didn’t replace it with anything else because I didn’t have anything else to replace it with.
Jon Orr: And what happened because you didn’t, let’s say you didn’t replace it, like what did you see? Like what was, what were you noticing? And maybe you didn’t notice, you’re like, I just, I’m supposed to just not do these anymore. Did I, did you see a difference? Did you feel like something, something needed to come in or? Because I think when you think about ditching it, it’s like, okay, well we need to do all problem solving. We just need to engage ourselves in tasks and get SIDS to kind of do the reasoning on their own and get the discourse happening. But then, Like, did that just work for you and your students?
Yvette Lehman: think you can imagine that, I mean, that year in second grade, I don’t know that it was as evident that it wasn’t working because we could still, the numbers were accessible enough that we could still rely on strategies like counting and skip counting. And that was, you know, developmentally appropriate. I think where I started to really see the result.
is imagine me, I actually taught the same kids in grade six, which was a cool experience. So my very first class of grade two, I taught again when they got to grade six. They are my most memorable class for sure. I had them twice. They were my first class. That’s when I saw the impact.
Kyle Pearce: Hmm. You know, it’s, it’s funny. And I think there’s a lot of people out there and educators specifically out there that also had that message. I know I had that message where I was sort of like, almost like trying to, in order to make it what I thought in my mind was accessible for all my students. This was when I was teaching grade nine and typically a class of students who have traditionally struggled.
in mathematics, I was like, well, if I could help them become really good problem solvers and like they don’t need to know their math facts because like we’ll just use a calculator for everything, you know, and like that was sort of my my first, you know, jump into this world. And what I started to recognize, you know, over time was, shoot, now they’re just memorizing what the punch in a calculator. And that’s also not that helpful. Right. And they weren’t able to think through some pretty basic, you know,
calculations. Now, they didn’t need to have an exact number, but to be able to just reason through right ahead of time what it was that we were asking them to do. I wasn’t providing that for students for a period of time. And it took a while until I started to recognize that. Doing like repetition is very important, but there has to be understanding with it. Right. So this is where I think we always come back to this middle, this middle ground of, you know,
there’s it’s somewhere between the two extremes. It’s not all rote memorization with no understanding and it’s not all inquiry and you know, just sort of like, you know, problem solving to do everything and no actual repetition. We do need to give students those reps and I, I try to apply the same thing when we think about sports, for example, it’s like in baseball where I’m coaching baseball right now, we could do grounders all day long and make it routine.
But if we never incorporate the actual thinking of the game, right? What do you do once you get the ball? You don’t always throw the first, you you have to think and you have to know where to go. But we do want part of it to be automatic. And I think when it comes to, you know, number sense and math facts and all of these things, it’s like, how do we take the best of what I was given as a student? Because again, there was some value there. There was some value. How do we take the best of that?
and add maybe some of the best of the parts that maybe were absent and bring those two things together. And I think, you know, now after many, many years of sort of, you know, trying this, and I always say like, unfortunately, you know, trying it on some students that may not have gotten my best, you know, the best side of me as an educator, we can at least as a whole, try to get a little bit closer to this middle ground that we’re really seeking out.
Jon Orr: Yvette, you, like when you were talking about the results in grade six, like you saw, like those are the choices you were making in grade two, grade six. Like some people are like leaning in going like, okay, tell me more about the results. Like were they impactful? Like was the things that you were doing in grade two carry forward all of a sudden? like your grade sixes were like just dominating or where, you know, tell us about what’s going on. Tell us, give us the details here, what’s going on.
Yvette Lehman: Absolutely not. No, they were not, John. What I noticed, and I think you already alluded to this, Kaya, like what I did, I think was create a safe space for learning, know, being vulnerable myself about math and honouring student thinking and, you know, highlighting a variety of strategies. But when it came to the cognitive load, of actually performing the computation.
We did not have efficiency and it was not done with ease. And the problem is when you are struggling through, you know, two digits subtract one digit with regrouping as part of a problem, when you’re putting that much time and energy just to figure out or you even maybe don’t even have the skills to do that, you really can’t get to problem solving.
Like either you’ve now gone down the wrong track. We actually just saw grade four and five students recently who were doing an assessment at the end of the year with subtraction with regrouping. And do know what they were doing? Which was shocking to me. When they had multi-digit subtraction, so it’s like, let’s say three digits subtract two digit, they had clung to the rule that you never subtract a smaller number by a larger number, which is again, a rule that expires, but they were switching digits within the subtraction. So if let’s say the tens digit in the first number, they were swapping the digit in the minuend and the subtrahend so that there would be no regrouping.
Jon Orr: hey, let’s just put that one up there.
Kyle Pearce: Yeah, you can’t, well, you can’t move. Yeah, you can’t. This number is small. You know, I can’t do that. Swap it around.
Yvette Lehman: Right, so now it’s like we have a cohort of students that, this is a blanket statement, okay, so like don’t take this harshly math community, I’m just gonna say there are some students within our community who didn’t have repeated practice of basic fact fluency when they were in my grade two class. They’re now let’s say in sixth grade and that computation is not only very
Jon Orr: There’s no borrowing happening here. Okay. Put an asterisk around this, folks.
Yvette Lehman: onerous and demanding for them, they may not even really, they still, like what we wanted was reasoning, right? Like it’s like we said, stop doing memorization because we want to support reasoning and problem solving. But if they can’t fluently work with all four operators with numbers up to a hundred, with ease,
Jon Orr: So this is like why the teacher’s like, well, let’s just go back to front loading. Let’s go back to memorizing so that we can get to the problem solving. And then for how do I do that faster so I can have more time problem solving? then you get this circle because it’s like, well, we got more problem solving. Let’s ease off on the timing for how much memorization and rote learning we’re going to do so that we can problem solve.
Kyle Pearce: Yeah, well, it’s funny too, because I think that the further along we go in the journey, right? And the bigger we’ll call it, the bigger the gap is in this number sense or fluency and flexibility. Like the more I challenging it becomes as the educator to say, like, is it too late? You know, like, is it too late for these students to get what I want them to have? And I would argue it’s never too late. Like, it’s only going to be helpful.
if even if it means doing subtraction when you’re in grade nine and you don’t have, it doesn’t have to be single digit subtraction, but you might have to start with single digit subtraction to help them understand the model and the strategies that you’re using. But when they start to get these strategies under their belt and they start to gain confidence, it’s like you can make such gains. And I think it’s such an important aspect and it’s something that we can do.
every single day, I would argue, at the start of class, because I feel like there’s so much time in education. I know time is always of the essence, but I feel like there’s so much time that we lose and it just slips by, you know? Like, it’s like we do bell work at the start of class, and usually that’s so you can do your attendance routine, for example, right? And it’s like, how much time gets dedicated there? And like, I would argue, how much of those minutes sort of
Jon Orr: Whoa, you just, everyone’s listening now.
Kyle Pearce: slip through the cracks that I could go, okay, I could be very intentional and do something a little bit different and actually get some big gains there in order to start to see students thinking a little bit more when they’re doing some of these, these pieces and really building their ability to become more efficient because it’s very difficult to be a very good problem solver. If everything is hard, you know, like if all the thinking, all the numbers, all the calculating,
is hard, it’s just a distraction. And then we think about those students who have the greater needs, right? When we have certain learning needs and how cognitively demanding some of that work could be and how hard that can be for them to try to keep up with the thinking and the rigor. I would argue it’s something that’s so needed and so necessary if we wanna have success with the other work that we’re doing, problem solving and such.
Yvette Lehman: I think that brings us to what should I have done? So when I was that second grade teacher and I was told, know, don’t rely on rote memorization, don’t rely on speed or mad minutes or flashcards to learn basic facts. We need to support reasoning. We need to build understanding.
what should I have done differently? Because I stopped doing the things that I was told were bad and that were detrimental to students’ identity as mathematicians and that weren’t getting us the results we wanted. But I myself didn’t have the capacity to replace it with something. So what’s our advice to past me on if we believe that fact fluency is important? And I don’t think any of us
would ever say that that is not a critical priority for a math education system. yes, we need our students to have fact fluency. We need them to be able to compute with ease. That shouldn’t be a barrier for access. What does the teacher need to do then?
Kyle Pearce: I’m looking at, was like, John, you get to go first.
Jon Orr: Well, like, we’re establishing that, you know, we need, we need definite practice here, you know, we need to be to bringing out the strategies in our classrooms that that that are that are promoting reasoning, like through what we would argue through context through problem solving, you’re developing a need to say there’s a strategy that evolves here. And then now let’s
Let’s talk about this strategy or this, maybe there’s a model that we’re highlighting today that uses a certain strategy. And now we’re going to make sure that you’re planning for practicing that strategy or selection a strategy that, that helps to solve problems. Like this is the way that we’ve talked about those things here on this podcast for, for a number of years of, of using problem solving to bring out the, need something here.
And let’s now go and explore why that’s something or bring that something forward so that it can help us relieve say tension in this problem or that we’re working on, or maybe it is something that we do initially to engage our students so that they have a tool to solve a problem with. But I think the part that we’re really saying here is that you do need to still plan for productive practice and purposeful practice around the learning goal.
the learning goal on the strategy or the method or the technique that you’re looking to students to say have and walk away with, which is about knowing the success criteria. What does it look like sound like? You’ve hit it, Yvette, that you do, like we do need to know what those strategies are ourselves so that we can then bring those out and we can make sure that they’re here. We need to think about like if I’m teaching multiplication, like what are these things that I do need to do that isn’t just
rote memorization and the memorizing of the tables. Like what are those strategies that help my students? I need to learn them too. And so it’s it’s recognizing that that’s still needed, but then recognizing you need to like take that on so that you can then design your lesson to include the practice, but also the problem solving that brings out why we need to practice.
Kyle Pearce: You know, the part I’m going to go right at, like, let’s say I was doing blank and now I not doing that thing anymore. Like I would say, what, what can I change about that thing? I was doing that activity, that process that I was using to try to help students build their, their fact fluency and really maybe not fluency, but actually having wrote, you know, automaticity of, of certain math facts. And I might say,
Are there any elements to that that can still be helpful to do that? But also, can I be more aware and conscious of what negative could come from how it’s happening? So what I mean by that is like, how are students feeling when they do this? And are they very clear on the very specific purpose of why we’re doing that activity? So for example, if a student is looking at this as,
individual and that it’s them versus themself to try to get better and try to promote. How can we do that in a way that it also protects them from feeling like they’re not doing what everyone else is able to do or achieve, right? Because here’s the problem. I think when we know that something’s having a negative impact on a student’s mindset because maybe they’re not at the same place as some others or maybe even the majority of the class around them, that can
open the door for them just shutting down completely. But the problem is if we completely remove any opportunity for them to get better at that, all we’re doing is pretending it doesn’t exist, which isn’t helpful either. That’s not gonna help that student. It’s actually gonna hinder that student. So the real, to me, I think the real thing that we could do is we could look at how do we get the benefit we’re after, but how do I do it in a way that it doesn’t have to feel bad or negative for those particular students? Again, baseball analogy.
We’ve got some kids that we can throw up there and pitch and they’re doing great things. And then there’s some kids on the team that are not ready to pitch and you almost are like, I don’t want to put them out there. I don’t want to put them through that. Well, so do we not help them to get better at pitching? So they just never become a good pitcher because now we don’t want, no, we have to find a way that we can give that student what they need to get a little bit better each and every day so that they can feel more confident and that they can.
Kyle Pearce: eventually do that thing that right now they’re not feeling super confident to be able to achieve. So while I’m not giving you an exact do it this way, I think the answer really lies in what have we done in the past? And then how do we do it in a way that will allow you to get the good out of that activity without maybe getting the bad out of that activity, right? Yvette, what would you say you’d do differently?
Yvette Lehman: I heard a few things. So I heard one is that we ourselves need to build our own fluency. That’s step one, I think. So I think that we need to focus on our own proficiency. And I’ll talk a little bit about ways that I know we’ve built our proficiency over the years when it comes to fact fluency. What I heard is that we need to give opportunity for practice. And I honestly think that we have in a lot of ways, I’m going to be, this is going to sound harsh. Okay.
but I know I harmed students by not giving homework and not giving them opportunities to just practice a skill. Because I think that even for myself, when I’m trying to learn a new strategy, right, if I’m working on a strategy and I’m trying to build my proficiency with that strategy, I have to do it a lot. And you talk about that all the time, Kyle, like those reps. Like I have to do it a lot with a lot of different numbers.
Yvette Lehman: so that it’s an automatic strategy in my toolkit that I use, you know, with that automaticity. And I also heard you say, Kyle, and this is gonna be a bold statement, but I used to be, yeah, I know, I used to be so anti-timed because I feel like that was really stressful for me as a student because I was so poor in all of the things we’re describing. But I think there is something to building efficiency and getting
Jon Orr: You’re full of bold statements today.
Yvette Lehman: more efficient over time through like what you’re describing is like is it like we’re graphing our own you know we work through some problems and we want to see if every day we can solve them a little bit faster using the strategies in our toolkit and we’re graphing our progress we do this with reading right where students read the same passage over multiple days and they’re trying to increase their fluency over time
I think there is something to measuring efficiency and increasing our efficiency and tracking our efficiency. That’s something that I would reconsider. And again, not to pin students against each other, not to make it a competition or to add pressure, but just that students have a goal for their own efficiency. I’m just going to share briefly with the community, you know, being somebody who can’t memorize facts without understanding what I, what I’ve done, you know, to better position myself if I was to go back into a grade two class next year.
One of the really critical parts of my own journey was problem strings, in particular, Cathy Fosnows mini lessons. Like actually, not only just doing them with my students, but doing them myself. Like I needed, and what I like about problem strings is that it naturally builds in those reps. Because if you engage in eight problems in a string, you’re using that strategy eight times in a row with different numbers and different relationships. So that to me was a really, you
critical part of my journey is just to not only use problem strings with my students, but actually carve out time in my own life, which I still do. Like I just bought the new problem mini lesson books that are the grade level ones from Kathy Fosno recently this year. And I commit to once a week carving out time to work through a problem string just to keep my mind. And my husband actually said this the other day. He said, you know, math is a lot like a second language. It’s like when we’re not using it routinely, we start to lose it.
Kyle Pearce: 100%, 100%. That’s, you know, I used to have this up on a bulletin board in my classroom where I said like mathematics is the universal language, you know, and, but I never thought of it like that, right? Which I think is a really important aspect. And then the interesting part is I think the more you dig into any language, so not only if I stop utilizing it, can I lose it.
But the more I utilize it, the more efficient you become, the better you can communicate in that language, right? And the more, we’ll call it elaborate, your use of that language can become. And what you’ve kind of highlighted here is really a huge part that we as educators, I know I didn’t know this until very late in my journey.
but I feel like very few educators recognize how important it is for us to be doing mathematics ourselves and not just knowing the example we were going to do in class, right? Like it’s actually like thinking about it differently and constantly learning. And as we do that work, it makes you so much more prepared to be able to handle anything you could come across in a classroom.
Right? And it’s like each and every day you become a better facilitator of mathematics instruction because you start to recognize some of the things kids might be doing that maybe a year ago or five years ago would be meaningless to you. Right? And when you see a student working through a problem and they’re off and it looks like they’re way off track, the more depth of understanding that I have, the better off I can read what they’re doing and actually start to make some.
decisions about what might be going on. And then of course I can ask them more to elaborate, but without that, I would just say like, it’s very hard not to just shut a student down and say like, just do it this way, right? But if I can see what they’re doing and I actually can kind of see the connection to some other aspect here, I might be able to kind of help, you know, bring them back towards, you know, the logic that, that is helpful for, solving that problem. So,
Kyle Pearce: I don’t know. I think what I’m hearing from you is the only way we’re going to get better at this is by getting better, you know, ourselves. And as we get better, we could then do more for our students in the classroom instead of, you know, essentially where we are in a lot of places, which is sort of this either or mentality. We can sort of get closer and closer to that middle. And I would argue it’s not a perfect middle, but it’s somewhere in the middle.
And I’ve heard you say this before is like the answer lies somewhere in the middle and we’re not gonna state it’s like a little more this way or a little more that way. And I would argue it probably moves a lot depending on the student and on the concept. yeah, I’m hoping that people will get a takeaway from that.
Jon Orr: Yeah. Well. For sure, for sure. it’s like, I think commitment, know, commitment is going to be based off what you can commit to. So for example, it’s like, I’m not gonna all of a sudden radically know and dive into every single concept that I’m teaching in grade two, and I’m gonna be an expert on it immediately so that I can then relay that information to my students. Like know that it’s going to take time, and it’s going to take a number of years to do that as well. So it’s like, can I commit to saying,
I’m going to make sure that I know this topic well, as it’s coming up and you know, down the road so that I can then develop that lesson or modify that lesson or, you know, and adjust it so that I engage in making sure that I have the purposeful practice, I’m bringing in these elements, I’m going to be like making sure that I feel confident with the math. But that might might be it for a while because you then you know, you know, you need to survive and you need to be thinking about something else like for a while there, when I was engaging this type of work.
I remember thinking that in this unit, this is the key lesson. So that’s where I’m going to make sure that I really dig into making sure that that lesson is involved well. it kind of like spill in it. What happens is it spills over into the before and after. And then, then I know that my mental bandwidth and my energy and my, learning that I need to do is really around that key concept in that unit. But then it’s like, well, what’s my, my, my next unit.
which is in a couple weeks, like what’s that lesson going to be that I’m really unpacking? Like I remember going through that process and then eventually it became like the process of like what part today am I gonna be really making sure that I enforce? And why I say today is because I taught say three different math classes in one day, three different grade levels or three different preps. As a high school teacher.
And I knew that when I was going through this process, I couldn’t commit to every class unpacking something, you know, really, really essential for students as I’m trying to learn this every day, because I couldn’t commit to that type of learning. You only have so much planning time or prep time to commit for that work. So it was like, well, what’s the one today that I’m going to make sure? Is it this course or is it that course or is it this course? Or maybe it’s maybe this year, I’m going to really focus on that course as really being the impactful
you know, the impactful learning that I’m going to do so that I’m better prepared and then over years of doing that type of work, you get better. And I think that’s like where you have to decide on where those commitments lie.
Yvette Lehman: So if we have teachers listening who are thinking right now, well, we’re heading, if you’re listening when this episode is released, it’s going to be June, we’re heading into the summer. What can you commit to? I like that word commitment because I think this is a commitment. What can you commit to over the summer to better position yourself to support fact fluency and just general computational fluency next year? So I’m going to give two ideas. The first one is the one that I already shared, which is
get a problem strings book and actually work through it yourself. Commit 15 minutes a day, 10 minutes a day of just working through problems and commit to building your own capacity by doing more math, committing to doing more math. The other recommendation is if you want to learn about strategies and you want to be able to identify high yield strategies for all four operators, then Figure Out Fluency in Mathematics by Jennifer Bay Williams and Johnson Giovanni is a great read, especially the
the one that is general, it’s not specific to each operator because it gives you seven high yield strategies that can be applied to all four operators. So if you want some, you know, a commitment to summer reading this summer, I think that’s the way to go. Cause I don’t know if we’ve actually said this yet on this episode, but we do believe that a strategies based approach is the way to solve this problem.
that we can build fact fluency, automaticity, efficiency, not through memorization, but through understanding or being able to use a variety of strategies with a high level of efficiency and understanding. But to get to that place, we have to build our own ability to use these strategies, as John already mentioned.
Jon Orr: For sure, for sure. And so we’ll put those links in our show notes. So as you just scroll down and click in there and you can kind of get to those links to add to your reading list and your, I guess, your math list as you’ve had as say unpacked here was it could be some summer learning for you. And if you do want to say take a little bit more time to do a little bit of digging into strengthening all six components of your classroom.
tree as we like to call it here. We talk specifically around, you know, with the branches of the tree look like strategies, what are our lessons need to look like, building, you know, practice, problem solving, those we call those the branches of our tree. But like many pieces that we talked about here on the podcast, as well as that in order for us to strengthen that component, we do need to build on our roots of our tree, which is our own proficiencies towards mathematics, our own
conceptual understanding of mathematics. we talk about strengthening that. That’s where that leads into that kind of say summer learning. can learn about all six components that we would recommend you digging into, which can be found over at makemathmoments.com forward slash report. Makemathmoments.com forward slash report and fill out your survey there and you’ll get your assessment on your six components of an effective mathematics classroom. Talk soon, everyone.
Thanks For Listening
- Book a Math Mentoring Moment
- Apply to be a Featured Interview Guest
- Leave a note in the comment section below.
- Share this show on Twitter, or Facebook.
To help out the show:
- Leave an honest review on iTunes. Your ratings and reviews really help and we read each one.
- Subscribe on iTunes, Google Play, and Spotify.
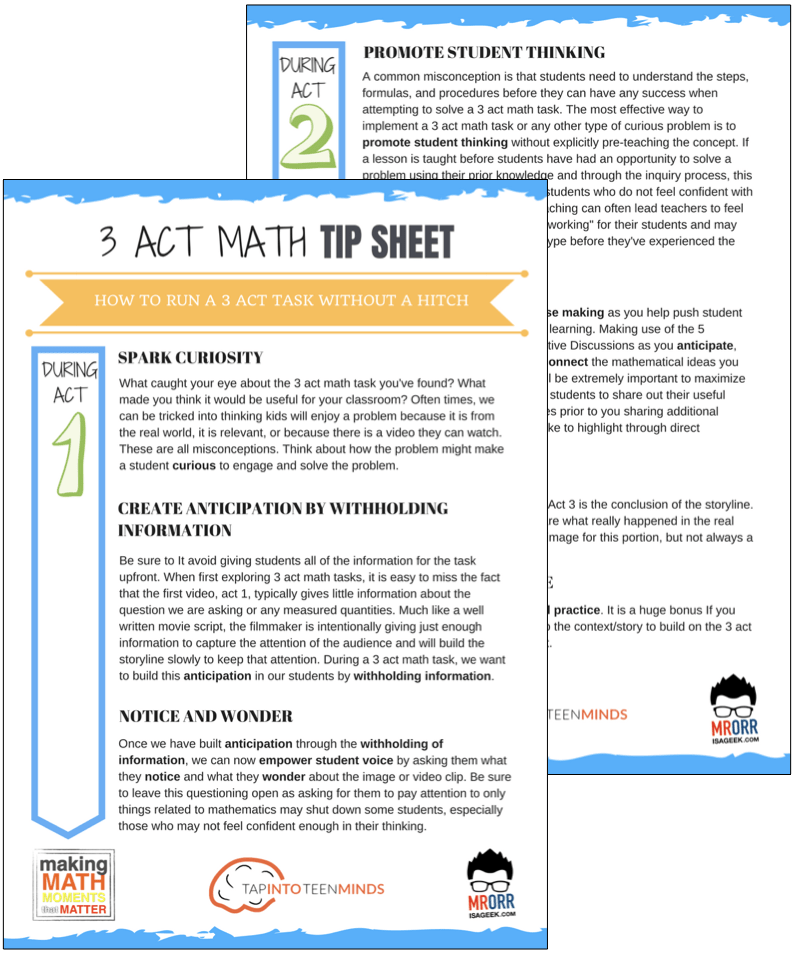
DOWNLOAD THE 3 ACT MATH TASK TIP SHEET SO THEY RUN WITHOUT A HITCH!
Download the 2-page printable 3 Act Math Tip Sheet to ensure that you have the best start to your journey using 3 Act math Tasks to spark curiosity and fuel sense making in your math classroom!
LESSONS TO MAKE MATH MOMENTS
Each lesson consists of:
Each Make Math Moments Problem Based Lesson consists of a Teacher Guide to lead you step-by-step through the planning process to ensure your lesson runs without a hitch!
Each Teacher Guide consists of:
- Intentionality of the lesson;
- A step-by-step walk through of each phase of the lesson;
- Visuals, animations, and videos unpacking big ideas, strategies, and models we intend to emerge during the lesson;
- Sample student approaches to assist in anticipating what your students might do;
- Resources and downloads including Keynote, Powerpoint, Media Files, and Teacher Guide printable PDF; and,
- Much more!
Each Make Math Moments Problem Based Lesson begins with a story, visual, video, or other method to Spark Curiosity through context.
Students will often Notice and Wonder before making an estimate to draw them in and invest in the problem.
After student voice has been heard and acknowledged, we will set students off on a Productive Struggle via a prompt related to the Spark context.
These prompts are given each lesson with the following conditions:
- No calculators are to be used; and,
- Students are to focus on how they can convince their math community that their solution is valid.
Students are left to engage in a productive struggle as the facilitator circulates to observe and engage in conversation as a means of assessing formatively.
The facilitator is instructed through the Teacher Guide on what specific strategies and models could be used to make connections and consolidate the learning from the lesson.
Often times, animations and walk through videos are provided in the Teacher Guide to assist with planning and delivering the consolidation.
A review image, video, or animation is provided as a conclusion to the task from the lesson.
While this might feel like a natural ending to the context students have been exploring, it is just the beginning as we look to leverage this context via extensions and additional lessons to dig deeper.
At the end of each lesson, consolidation prompts and/or extensions are crafted for students to purposefully practice and demonstrate their current understanding.
Facilitators are encouraged to collect these consolidation prompts as a means to engage in the assessment process and inform next moves for instruction.
In multi-day units of study, Math Talks are crafted to help build on the thinking from the previous day and build towards the next step in the developmental progression of the concept(s) we are exploring.
Each Math Talk is constructed as a string of related problems that build with intentionality to emerge specific big ideas, strategies, and mathematical models.
Make Math Moments Problem Based Lessons and Day 1 Teacher Guides are openly available for you to leverage and use with your students without becoming a Make Math Moments Academy Member.
Use our OPEN ACCESS multi-day problem based units!
Make Math Moments Problem Based Lessons and Day 1 Teacher Guides are openly available for you to leverage and use with your students without becoming a Make Math Moments Academy Member.
Partitive Division Resulting in a Fraction
Equivalence and Algebraic Substitution
Represent Categorical Data & Explore Mean
Downloadable resources including blackline masters, handouts, printable Tips Sheets, slide shows, and media files do require a Make Math Moments Academy Membership.
ONLINE WORKSHOP REGISTRATION

Pedagogically aligned for teachers of K through Grade 12 with content specific examples from Grades 3 through Grade 10.
In our self-paced, 12-week Online Workshop, you'll learn how to craft new and transform your current lessons to Spark Curiosity, Fuel Sense Making, and Ignite Your Teacher Moves to promote resilient problem solvers.










0 Comments