Episode #215: What To Do Instead of Rushing to the Algorithm – A Math Mentoring Moment
LISTEN NOW…
WATCH NOW…
Together we help Megan see how starting with models and strategies before rushing to algorithms will strengthen students’ proficiency.
This is another Math Mentoring Moment episode where we talk with a member of the Math Moment Maker Community who is working through problems of practice and together we brainstorm possible next steps and strategies to overcome them.
You’ll Learn
- How to approach multiple representations and why they are important for building mathematical proficiency;
- Why it is important for students to show how and why they got their answer;
- Why building fluency and flexibility with strategies and models before introducing an algorithm is extremely important; and,
- What you might do if an algorithm was introduced before fluency and flexibility was achieved with prior strategies and models.
Resources
Sowing Seeds – 2-Digit By 1-Digit Division Unit
Niagara Falls – 3-Digit and 2-Digit by 2-Digit Division Unit
How to Teach Division: What Teachers Need To Know [VIDEO]
Take Your Learning To The Next Level:
Join the Make Math Moments Academy
District Math Leaders:
Learn if your district is a good fit for our Make Math Moments District Improvement Program

FULL TRANSCRIPT
Megan Garner: I think that's probably what was intended when the teaks were written. They just, no one had explained it to me. And just understanding that the fluency and what I really want them to be able to do is to look at a problem and be able to determine reasonableness and determine which strategy works well for them. That's really where I want to go with it because I've been drilling in your standard algorithm and your traditional methods for years that it's just not going to work like that for everybody. But I think I just want to explore how do I inaudible -
Jon Orr: In this episode we speak with Megan Garner, a fourth grade math teacher from Liberty Hill, Texas. Megan is just in her fifth year of teaching and is aiming her sights on helping her students develop flexible strategies around division and other basic number sense skills. But she's finding it a little frustrating when students want to always resort to that standard algorithm.
Kyle Pearce: Yeah. So together we're going to help Megan see how starting with models and strategies before rushing to algorithms will help to strengthen students' proficiency and flexibility. This is another Math Mentoring Moment episode where we get to chat with a member of the Math Moment Maker community just like you, who's working through problems of practice and together we brainstorm possible next steps and strategies to overcome them. Here we go.
Welcome to the Making Math Moments That Matter podcast. I'm Kyle Pearce.
Jon Orr: And I'm Jon Orr. We are two math teachers from makemathmoments.com. Who together...
Kyle Pearce: With you, the community of Math Moment Makers worldwide who want to build and deliver problem-based math lessons that spark curiosity...
Jon Orr: Fuel sense making...
Kyle Pearce: And ignite your teacher moves. Welcome everyone to another math mentoring moment episode with a fellow Math Moment Maker just like you. And Jon, I don't know about you, but chatting with someone who's been teaching for five years yet is pushing so deeply into trying to ensure their students have more than just the algorithm is something that makes me feel so great about where we're headed for math education. I do know about you, Jon. I know your story, so I do know this about you, but I feel like it took you and I a lot longer to see that math class was more than just sort of memorizing and mimicking the steps and the procedures.
Jon Orr: And just from saying that and noticing that so many teachers we talk with on the podcast, I think there's a lot in that boat too, Kyle, which means I feel like there's a lot of momentum for teacher change, for math instruction change, especially happening at younger ages. And so imagine these younger teachers, you're saying, we didn't do that for the first 10 years of our career, but we've got a whack of teachers who are doing that and think of the wave that's going to happen as they get older. And then they've got that skillset even far deeper than we have our skillset because they started so much earlier, so excited for this wave and to be part of that wave coming to our future. So excited for that. Now let's jump into this episode because we've chat with Megan all about kind of flexibility strategies, fluency strategies, how best to get your students to understand that they can use multiple strategies. And so we've all about that. We want to share that conversation with you. So let's get to it.
Kyle Pearce: And hey, listen, if you've got time, flip over to YouTube to check this out. Because later on we actually dig in with the document camera. So if you want a little more context here, a little more visuals to go along with it, hit us up on YouTube. But otherwise listen in and here we go.
Jon Orr: Hey there Megan, thanks for joining us here on the Making Math Moments That Matter podcast. How you doing this evening?
Megan Garner: I'm doing well. How are y'all doing?
Jon Orr: Awesome. Awesome. And do us a favor and do our listeners a favor. Let us know where are you coming from, what's your teaching role look like right now and fill us in a little backstory on the teaching journey thus far.
Megan Garner: All right, so I am a fourth grade math and science teacher in a town called Liberty Hill in Texas. It's about 30 minutes from Austin. This is my fifth year teaching and I did third grade, then fifth grade, and now fourth. So kind of right in the sweet spot in the middle. And I've been lucky enough to teach math every year and I just recently started teaching science as well.
Kyle Pearce: Awesome, awesome. So you've had some experience. So you've been teaching math it sounds like for the most part for your entire schedule. Now you're doing some science as well. How are you liking that? Would you rather be just going straight up math so you could focus or are you kind of liking the variety?
Megan Garner: Yeah, my boss will probably hear this. No, I like having the variety. I do. I'm very aware of how much I love math and I feel like I'm very strong at math and understanding the content and just kind of digging deep into it and I need to get there with science. I don't think I'm a bad science teacher. I know that man, I am stronger on the math side.
Kyle Pearce: There you go. I love getting people's perspectives on that. I know that there's some educators who they just love being with the same group of students all day long and kind of rolling from one subject to the other. But I'm definitely the advocate of sticking to a subject area so that you can really dig in, really understand. And I think with math especially, I was just working with my son upstairs before I hopped on and he struggles with spelling and I realize working with him how little I know about helping students understand how to spell. So I can only imagine again if I had to teach all the different subject areas. So thanks for giving us a little perspective there. Before we dig any deeper, we want to roll back into your past, into your math experience. It sounds like you're kind of enjoying this role as a math educator. Go back to that K to 12 experience. What would be that math moment that pops out in your mind? Is it positive, is it negative? Is it somewhere in between? Take us on that journey.
Megan Garner: It is definitely positive. I remember the exact location, I remember where I was when I learned about variables.
Kyle Pearce: Doesn't everybody though?
Megan Garner: I feel like it's not always positive, but hopefully, I don't know. But I remember they gave us balances and they gave us two different colored ponds and they're like explore and they had different weights and we're messing with them and finally we're like we wanted to balance it and eventually figured out two red ponds is equal to three blue. And I was just like, my mind was blown that right there. It was a puzzle. There were two things that looked identical, but they represented something that was a number and I knew it was a number, but what I was looking at wasn't a number. And it just completely opened up a whole nother world of math and possibilities for me.
Jon Orr: That is very, very interesting. And I'm wondering if you could elaborate a little bit more on that, a world of possibilities for us before we kind of venture forward. How did that kind of open doors or what did that look like for you after it was like, oh my gosh.
Megan Garner: I really wish I knew what instruction looked like in the classroom when I was say a fourth grader because I feel like I had been learning it and it was probably a lot of just memorizing things and just kind of drill it in and lots of worksheets. In that moment I realized that I had seen a puzzle, I had seen a math problem that I had never seen before. I'd never seen anything like it, and I was able to solve it. And I realized in that moment that you could represent things mathematically that weren't necessarily, they didn't look mathematical on the surface. And just as a person that's not a teacher outside of here out in the wild, I think mathematically if I'm running, I'm like, man, I'm one eighth of the way done. inaudible. Kind of just assessing everything that I see and I do through a mathematical lens, it helps me feel grounded. I feel like when I can mathematically assess the situation, I know where I'm at and I know where I need to go. And for me, I need that in my life.
Kyle Pearce: The analytical mind. I love it.
Jon Orr: Math is like a grounding, it keeps us level, it keeps us humble, but also it keeps us kind of moving forward in a sense. And I think these things stick with us for reasons and they stick with us into our teaching journey as well. How do you think that moment has influenced your teaching style in the classroom?
Megan Garner: I don't think that it really influenced me to start off with, I did the alternative certification and I started in January when I was first hired and I was just kind of thrown in and just kind of finding my feet as I was going for sure. And I was kind of just going with what people were giving me. And I talk a lot, I talk with people though with the kids, with the students, and just talking with them about how I see things and how I analyze things and having those discussions with them has really helped me understand how that particular moment shaped me and how powerful it was. And so empowering for me to be able to do that on my own. And I in turn want to give that back to the students. And I think, and that's part of the reason I had this pebble in my shoe and I sent in the question is I think about math in so many different ways. Whenever I am looking at questions and if I'm solving it in my head while they're working on something at their desk, I realize that I'm doing things that I want them to be able to do and I just want to be better to fully execute that and make it happen for my students, if that makes sense.
Kyle Pearce: I love it. I was going to ask you for a quick win here, but you've already, I feel like you've given sort of a quick win in terms of even just your own math moment and how you want to bring that out in your students. So I can almost envision what that probably looks like and sounds like in your classroom. So let's start digging in here a little bit. I'm wondering can you dive a little deeper there because we are going to ask you we're curious about that pebble in particular. Maybe start with what's going well and then maybe we can kind of shift to where maybe that pebble starts showing up in that shoot where things start becoming maybe more challenging or more difficult along the way. Do you mind taking us on a bit of that journey?
Megan Garner: Yeah, so for many years I struggled with looking at the teaks, looking at the skills and it saying students had to be able to show mastery solving a problem two different ways. And I was like, why would I spend twice as long teaching them to solve it with a standard algorithm and with the expanded form or whatever the other might be, just so they can answer it two different ways on the test. So it did not seem like a good use of time and I didn't really feel like I was doing a whole lot of good by doing that. And I don't remember specifically what episode it was that I listened to, but it was talking about the mental math and then the fluency versus automaticity episode changed my life y'all. Thank you. And just understanding, I think that's probably what was intended when the teaks were written, they just no wanted to explained it to me and just understanding that the fluency and what I really want them to be able to do is to look at a problem and be able to determine reasonableness and determine which strategy works well for them.
That's really where I want to go with it because I've been drilling in your standard algorithm and your traditional methods for years that it's just not going to work like that for everybody. But I think I just want to explore how do I best meet the needs of kids that see it different ways. In talking to them, I've realized that I see problems multiple different ways when I'm looking at them and I quickly choose the strategy that I know is going to work best in that moment and I just want to know how to get them to that point to where they have the confidence and the knowledge and the skills to make that happen.
Kyle Pearce: Gotcha, gotcha.
Jon Orr: Mm-hmm, mm-hmm. What are you doing currently in the classroom to... You're witnessing this pebble, you're feeling the pebble and right now you're probably all of us who when we have these pebbles we kind of try to shake them loose a little bit and see what happens. And so what is that shake look like for you right now?
Megan Garner: When we come in I have kind of my warmup routine and in there two or three days a week, I have a puzzle up there that has five different lines and different pictures just like images. It's from Mashup Math.
From there and y'all won't believe this, but I have them give me a variable so I don't have to redraw those pictures when we're solving it. And where I've gotten to now after the first few months of going through and solving them is whenever we have two variables on the same side of the equation, I'm like, how could we rewrite that possibly using the inverse operation to solve it? So we plug in a value that we've just figured out and now we only have one variable and it's on one side of the equation and what we know is on the other. And so I'm kind of exploring with them looking at a picture and then realizing what it's asking and then how are we actually going to solve it. I feel like when they see the shift from one side of the equation to the other, it helps them kind of expand on that flexibility.
Kyle Pearce: Yeah, it's interesting because kind of going all the way back to your initial reference of some of the standards around sound like multiple representations, being able to be fluent and flexible with say two approaches, standard algorithm and maybe some other approach. And here it sounds like in that activity you're really trying to draw on again that fluency and that flexibility piece. You're trying to ensure that students aren't just solving it the same way every single time, but actually like, hey, what happens when we do this or hey, what happens when we do that? So when you're doing that sort of activity, where is this challenge sort of emerging for you? Where are you getting hung up? Are you feeling like you're losing students? Are students having a hard time understanding why it's important to be flexible or fluent here? Take us a little deeper.
Megan Garner: I don't think most of them have realized why it's important to be kind of fluid and flexible with it. I do have a few kiddos that have really latched onto, I have one friend that multiplication facts, they're not sticking and he is very, very good at taking one of the factors. We're going to split it in half and then even if he doesn't know the half, he's like, oh, if it's a double of something, I know that I can add my doubles instead of multiplying by two. He's got that down and he builds his way back up and he is one kiddo that is really taking off night and day difference. Most of my kids that are able to rearrange the equations, I feel like they just think it's fun, which is okay with me if somebody thinks math is fun.
And then I have some other kiddos that they see it and I know that the information's sinking in, but it's not something that they're wanting to in turn try on their own to do later. For example, they just started learning long division, that's what we do in fourth grade here and we just introduced remainders and one of the questions required him to do 30 divided by seven and most of my kids are like, okay, I'm going to do some long division here for 30 divided by seven. I was like, let's think about it. Let's think about what you guys know. And just kind of getting them to realize that that is not always the most efficient option for solving a problem.
Jon Orr: Okay, yeah, I see a little bit of what's happening here. Megan, I'm curious about when you present these puzzles, these problems, some students are maybe solving them in different ways and some aren't and they're kind of just resorting back to a particular strategy. I'm curious, what does the consolidation or the connect part of your lesson look like for you? In the sense that I'm trying to see that the problems presented, kids are working and then when you're seeing solutions, what is your move next?
Megan Garner: So when we're doing that, it's a whole group.
Jon Orr: So everyone's doing and you're taking suggestions from the big group and you're maybe modeling that up on the board from what the group is saying.
Megan Garner: I am and it's a no pencil time. I don't want you writing on your paper, I don't want you figuring out stuff on your paper. I want to talk about it. And everything I'm presenting is things that could be done with mental math or with estimation and we can get there. So that's how it's presented. The pencils weren't always like a no at that time, but I saw a lot of kids that were still going with the one way that they knew and I really wanted them to focus on not so much getting it right and getting it done quickly, but how else can we do it?
Jon Orr: So you're bringing these strategies from them and maybe are you interjecting with any ideas to yourself leading that same math talk time?
Megan Garner: I am happy to report that I've been able to pass the torch somewhat and we're getting better at it. It's been probably about two months since I started really asking and let's look, how can we rearrange this so that it looks like an equation that we're used to solving? And if it's any kind of repeated edition, I'm like, no, what else can we do? What's more efficient? Those poor kids are like, "Oh, Miss Garner's talking about efficiency again." What can we do?
Jon Orr: Right. And so what I'm hearing is you're feeling some successes in small pockets here. This is often something that we think about when we have pebbles and I think about when I have pebbles is I ask myself, what does it make me feel like what I'm doing isn't the right thing? What isn't working? Because you're describing some great moments here, but you're still going like, ugh, it's not it, but how do you know it's not it?
Megan Garner: Yeah, I'll see, like today I had a student that was doing 30 minus 28 and we got 12, and I know that if they'd have just been like, oh, if I'm 28, I only need two more to get to 30, and if they'd just thought about it a different way, we wouldn't have needed to even write it down to do it, but we did. And then that brought in struggles with regrouping and it just showed an underlying issue that is bigger than just the regrouping, just not understanding the relative values and they have more skills that they can use and they're just kind of stuck in a rut.
Kyle Pearce: Hmm, interesting.
Megan Garner: That make sense?
Kyle Pearce: Yeah, no, totally doesn't wondering. I want to dig just a tiny bit deeper into let's say the actual problems students are solving here. I'm curious, would you say that the problems are typically with context, so a contextual problem where there's call it a story problem where these quantities are representative of something in that you can imagine in your head like they're dealing with apples or they're dealing with whatever that context might be. Would you say it's more contextless or sometimes we call it naked problems where they're operating or they're solving or they're evaluating, or is it somewhere in between? What would you say if you had to pick one of those three options there?
Megan Garner: I would say we're still at the stage where I'm seeing these types of struggles with just the computation, like no word problem or context in there. The way our units are kind of set up is they're fairly isolated at the beginning and what's coming up next is going to be all our operations where we're really assessing the situation and what type of problem it actually is. I talk about it all year, but as far as where I see the error pattern starting, it's definitely still at the computation level. I don't think that the context is necessarily contributing to that.
Kyle Pearce: Interesting. You know what? I'm more curious, are you giving them contextual problems or not that it's adding to the problem. I'm wondering are you starting with context or are you starting more with just computation problems and then once they've achieved a certain level of success with computation problems, then we add in the context or the storyline?
Megan Garner: I would say we're probably doing two, maybe three days if I'm introducing something new like long division with just the computation and then adding in the word problems. I feel like especially for fourth grade in division, this is a whole nother world for them. We were dividing within a hundred before and it was something they could kind of think about on their own. I feel like it was overwhelming seeing the bigger numbers and I wanted to give them a couple days of just kind of exploring it first.
Jon Orr: Right, right.
Kyle Pearce: Yeah. And I'm kind of wondering, let's use long division as an example. So let's say you're introducing long division. What might a problem sound like you had given the 30 divided by, I can't remember if it was like eight-
Megan Garner: Seven.
Kyle Pearce: ...Or seven? =Would that be sort of your starter as like, hey, 30 and divided by seven to introduce long division or what might that look like or sound like?
Megan Garner: We started with multiples of 10 and multiples of a hundred of the basic within 100 multiplication facts. So we know that 25 divided by five is five, so then we're going back to the place value knowledge. So 250 divided by five is going to be 10 times greater, started with that.
Kyle Pearce: Super cool.
Megan Garner: Slowly. Before we went in, so with the compatible numbers and then we also expanded upon compatible numbers and exploring the difference between rounding versus a true compatible number to get a reasonable answer.
Kyle Pearce: Interesting, interesting. Now, would you be modeling that for them because you know that they could figure it out? So it's interesting because something that kind of jumps out at me as this, at least if I was to maybe articulate what I'm hearing this challenge is involving or this pebble in your shoes involving is it's like we're introducing these algorithms or these procedures long division, but then it seems like sometimes the question doesn't fit the algorithm. It doesn't seem like a reasonable time to use the algorithm, but then students are trying to use it in some cases instead of maybe using other strategies. Would that be highlighting that pebble in a nutshell or?
Megan Garner: That was one that came up today. I think I see good rich discussions happening with the compatible numbers and just understanding multiples of 10 and how we can use that to understand if our answer is anywhere close to correct. But then once the discussions are gone or the discussions are over and they're not at my table, are not working with me, it's like we've forgotten that we had that skill and I'm struggling with getting them to understand the importance of it. And then on the other end, I have kids that are like, oh, you can just estimate. I don't have to show my work on anything. And they just kind of go on and they round everything after that. And I think that was kind of the anarchy I was alluding to whenever I sit in that pebble, I was like, I have kiddos that aren't utilizing it when I know that if I'm there with them and supporting them they can. And then I have other kids that are like, oh yeah, that's the only way to go. I'm going to use mental math for everything and I'm out of here. Yeah, my own kid included. My goodness, y'all. My own kid.
Jon Orr: Megan. So if we gave you a magic wand that took you into the future and the pebble is solved, it's already solved, right? You've got it figured out, it's ready to go. I want you to imagine what does your classroom look like on these math talks? What should that look like for you?
Megan Garner: Just the being able to tell me how and why they got their answer. Just, I multiply these two numbers. I knew I needed to multiply because I saw equal groups and I was looking for the total and I chose this solution and I got there this way. Got it. There isn't a specific answer that I want. I just want them to feel comfortable and confident I guess that that's really what I want.
Jon Orr: Got it. Now when you see what they wrote on their board or on their desk or maybe they're telling you, right? I often ask my students to draw, write as much as they can before they tell me what does that look like right now? Doesn't have to be that problem you talked about, but just imagine what are you seeing? We've already got the answer. They're flexible, they're ready to go. They're about to tell you. What does that look like on their desk or their paper.
Megan Garner: I feel like I'm at the point where having groups of three or four kind of work together and I've strategically kind of grouped them at their desk working together. I'm at the point where I feel like I get the richest conversation and I get the most out of it for everybody. Like I said, when they're working together, they're working with me. I'm getting decent answers, but it's when we take that away that it's not happening for everybody.
Jon Orr: What do those answers look like though on pages? Is it just calculations or are there pictures.
Megan Garner: Oh no I make them write it. I tell them they're in the math court of law and their answer is going to justify their position. They better convince me and the jury that their answer is and tell why.
Jon Orr: Got it. Right, right.
Megan Garner: We do our writing prompts every week. So I start them at on Monday with a quick check for what we're doing for the week. It's not graded like going on report cards, but we work towards Math Stream throughout the week. And then one of the assignments they have to do before they take their quiz at the end of the week is a writing assignment where it's almost never requiring them to complete any sort of computation, but it's digging deeper into the how and the why behind a concept. And then they switch journals with somebody and they have a rubric and they do a peer review and kind of grade it on content and clarity and were we using academic vocabulary. And I tell them like, if you can write about math, you can do it. For some of them I think they still think I'm quite evil, but we're getting there.
Kyle Pearce: I love it.
Jon Orr: When I imagine my students to be flexible and fluent, which means they're swapping out strategies when one doesn't work or when they look at the numbers they're seeing this strategy might be better here. I might be able to decompose these two things here because I'm looking at the numbers. When I imagine that solution in the future of seeing what's written on their desk, I'm usually imagining in my mind visuals that accompany say these strategies. So when we talk about models, we talk about strategies that go with those models. When we're working with proportions, are we drawing number lines that show scaling and tandem along those number lines? And students don't come up with these on their own. What happens is when they speak answers, we kind of do an automatic start to draw these models that help them understand their strategies that they can be visually represented.
If you're doing multiplying, you're drawing an area model. But when they talk about, oh, I multiplied these two things together, I'm at the board kind of going, oh, can I draw it this way? You're describing multiplying these two digit numbers together, or maybe you're dividing these digit numbers. I'm going to draw this area here. And when you say this multiplied by this and there's this many groups, is it okay if I draw this many things here and this many things?
I find that when I model their thinking using visual models that I want them to use so that they can be flexible. Okay. It puts it in their mind so then the next time they go to do a problem, I see them drawing those models. Because a lot of the times they won't draw visual representations of some of the thinking and the strategies until they see me model it for them using those and then it kind of spirals from there. That might be something that can be in your arsenal is start to think about how can I represent their thinking since you're already doing these great math talks and hearing great strategies, giving them a tool that they can use to be flexible. Like say an area model if you're multiplying number line, if you're thinking about proportions or counting or multiplying, any sort of tandem quantities. Kyle, what do you think about this model strategy moving forward for Megan?
Kyle Pearce: I was right with you there, Jon. I had this all prepped up here. I'm going to pin this here, spotlight this for a second. And those who are listening, you can check this out on YouTube, but just kind of going back even to this ideas while something that kind of jumped out at me, which I was envisioning myself in the classroom when I was asking about the context piece. Because what we tend to do, or at least what I used to do and the way I remember learning was we start with calculations and then we slowly add context later.
And this is sort of something that Jon and I have been on a journey to realize that actually context is sort of the glue that allows students to understand what's happening, which allows them to build more flexibility. So if my end goal and on the screen for those who are with us, if my end goal is long division, there's a couple things that I can do in order to get that to emerge in my classroom. I could ask students and now here's the tough part with division, my first question is, what type of division do I want to elicit here? Because if I just say 30 divided by seven, there's two ways we can look at that. When I add context, it becomes more clear because I could say that I have 30 apples and I want to divide 30 apples into seven baskets.
Megan Garner: This one did have context.
Kyle Pearce: Oh did it?
Megan Garner: My apologies.
Kyle Pearce: OK, awesome, what was the context?
Megan Garner: This one did but there were other ones that didn't. I have 30 cupcakes. My joke is always cupcakes. I'm always talking about eating cupcakes. I was like, I have 30 cupcakes and I want to eat the same amount every day for seven days. And then I gave them two questions. Because we just started interpreting remainders and it was how many will I be able to eat each day? How many would be leftover?
Kyle Pearce: I love it. So now if I want to come at this. Now, maybe you guide me here because this particular problem, if it did have context, amazing. My wonder is did you ask them to solve the problem before introducing long division or did you say, here's long division now I want you to try this problem. Or what did that look like or sound like? Because maybe I've got it wrong in my head of how that might have looked or sounded.
Megan Garner: This is week three of long division, but this is week one of remainders and this is the first time they've been introduced to remainders. So numbers are smaller and I did not anticipate that we would go straight to long division for 30 divided by seven. I did not see that bump in the road coming.
Kyle Pearce: Oh, interesting. Okay. Now I guess my wonder would be is let's partake for a second that we were just introducing long division. If I'm introducing long division, what I want to do is not introduce it at all and actually have kids solve it with whatever tool they have. Because what I think I heard you say was your challenge was students were using maybe an algorithm when maybe there was other methods that could have helped them get there. So one of the keys when we're introducing an algorithm is to make sure that they're really fluent with other strategies that are going to get closer to how that algorithm actually works. So for example, if we're looking at seven days, if I look at it this way and go, okay, well I have seven days, and some students might even think, okay, well if it's seven days, then it's like, oh my goodness, okay, well seven is not fun to partition, but I'm going to do my best anyway.
So there's 1, 2, 3, 4, 5, 6, 7 days just like that. And I'm trying to figure out all together, all of these days are going to require 30 cupcakes in total here. What I don't know is actually how many are in each one and what you're doing when you're asking this particular problem, 30 cupcakes, seven days, I want to have the same number per day. That's actually revealing a rate which makes that partitive division. So I'm going to take the 30 cupcakes, I'm going to chop them into seven different groups. So you can kind of see the groups outlined here. If kids don't know the algorithm, they're probably going to do something like this. Some kids might fair share and they go, okay, well one for you, one for you all the way through. Okay, seven are used up. Maybe they go, okay, now 14 are used up. Oh, some kids might go, wait 14. I know 14 plus another 14 is going to be 28. Oh my gosh, there's going to be four in each group.
Megan Garner: And I think my struggle was that my students that are still working on mastering long division didn't realize that they had this tool in their pocket and I feel like I'm having good math talks and I feel like I'm showing them different things and I don't know how to get them over the hump to where they remember and they're using that and they know that they can.
Kyle Pearce: Well, and I guess that's kind of where I want to lead this conversation. And this is only an idea and only you'll be able to test this theory out in your classroom because we're not there and we only hear this very small segment of what's going on in the classroom. But my wonder is whether the algorithm maybe was introduced maybe too soon before students were actually flexible and fluent using the strategies and the models. So on the screen here we have the array is the model that I've used. Now for a lot of students, it's not going to start as an array. What a lot of kids are going to do is go seven-
Megan Garner: inaudible. Yes.
Kyle Pearce: And this is where we as the educator have a lot of work to do to help them go, okay, listen, it's fine to go one for you, one for you, one for you and do this.
But wow, imagine if we could get this more organized. You talked about efficiency earlier. The kids are like, ah, there's that efficiency word. We can be more efficient here and it doesn't have to be long division. More efficient from here would be taking all of these different cupcakes out of these circles and putting them into rows and columns to help students emerge this idea of the array. And they need to be really flexible with that model before moving to an algorithm. Otherwise they're like, well geez, if this feels like I'm memorizing it because I'm not fluent with the array yet, and then you introduce this algorithm, they're going to be like, what's the one most recently that we used? It's long division, so I'm going to go there. And long division works but the key would be when I can get to a place where kids can pull out this strategy, this model, in this particular case the array is the model, but the strategy might be fair sharing that they one by one fair shared, or maybe they did two by two fair sharing.
That would be the strategy. Once they've got that down where it's like second nature, then in only then do we start to now help them see how this actually works over here where you start to go, wait a second, what did we do first? We put one in each group. Okay, so I want one cupcake times seven days and over to the side I go, okay, I just want to mark that down. It's like, wait, so I used up seven cupcakes, I'm going to put them right here and let's figure out how much do I have left? Oh, I've got, wait a second, 23 cupcakes left. And I go, okay, what did we do again? We fair shared another seven cupcakes. Okay, now I've got less cupcakes to work with. So now I'm at 16 cupcakes. What did we do then? We want, wait a second, these two groups right here, if you remember, for those who are listening, you're like, what's he talking about?
But these two groups right here, we knew were 14 and we're like, wait a second, there's another 14 in here that's two cupcakes per day. That's that extra 14. And now we have these two remainder left over. All we've done now with this long division is we've done their strategy that they used and we helped them to see that their strategy is baked into long division. They're actually not different. The model is different. This one's very symbolic, but you'll notice this one's more flexible. It's not the traditional long division algorithm. You'll notice I chunked it in a very friendly way to really help them see we did one cupcake per day, then we did another cupcake per day, and then we did two cupcakes per day. And you can see that one cupcake, one cupcake, two cupcakes, and all of a sudden it's like, wait a second, all the same numbers are emerging.
Here's a seven, there's a seven, here's 14 right here. There it is right there. 7, 7, 14, and we had 28 and there's two left over. I've got the same exact math happening here with a different model, a different representation that we have here. So I guess in summary, what I'm wondering is if there's maybe a topic coming up where you're like, Hmm, I've got to get them to this algorithm, to this procedure, but I don't want to find myself in the same situation where students are sort of going, forget everything else I've ever done in my life and now I'm only going to use this one thing. Maybe taking it a little slower, Jon, and I call it avoiding the rush to the algorithm. Not saying avoiding algorithms, but avoiding the rush to getting to the algorithm I think is maybe something that might give students maybe a little bit more time to actually build in that fluency and flexibility versus maybe just going, okay, I'm just going to go to the last strategy that we focused on because it's got to be the most efficient. That's the assumption that students make. What are your thoughts there?
Megan Garner: Yeah, I'm glad tomorrow's a Saturday, so I can put this into use tomorrow. I love it. And I can see how doing that for all of them, division's the last algorithm were going to be really tackling in fourth grade, everything after that is geometry and other things like that. I can see how if I had started that sooner, it would have huge, huge payoff whenever it came time to like the all operations unit where we're really having to think and assess the situation and how that could help. So I'm just going to work on a plan to undo any damage I did with algorithms this year and salvage it.
Kyle Pearce: Well never look at it as damage. It's definitely not. But one thing that you could do, because even though you might not have necessarily a new algorithm coming up, maybe the next time, say for example long division, next time that comes up, maybe you intentionally give them a problem.
Megan Garner: Oh, for sure.
Kyle Pearce: Maybe a lot of kids go straight for the algorithm. Maybe you model it with another model, whether it's the array or like Jon said, maybe the number line, whatever tool you think is going to be helpful for that particular context, and then help them to explicitly see the connection. And I have a funny feeling, a sneaky suspicion that if you do it sort of like what we just did here where they're like, oh my gosh, they might not realize how closely connected they really are. And the reason why I say that is because I taught for 15 years and I had no idea that there was another way to show how long division worked.
I just never asked a question, I just did it and that was it. But now I'm like, wow, when I see those representations and going all the way back to the initial struggle of showing it in multiple ways, helping kids to see why that's valuable. And the way I used to think as well was like, why would I spend double the time doing it two different ways? It's like to actually strengthen that connection, the connections that we make between those representations can actually be the thing that sort of keeps kids grounded, especially when things get hard or too abstract down the road.
Megan Garner: Oh, I'm so excited. They worked on that problem yesterday and some of them finished it up today. So when they come in tomorrow that 30 divided by seven is fresh on their mind and I'm am ready to have that moment where they're just like, mind is blown like, oh. Oh, I can't wait. Thank you so much.
Kyle Pearce: Do you promise to let us know how it goes?
Megan Garner: Yeah. For sure.
Jon Orr: Awesome. Yeah.
Megan Garner: And I promise to keep using that strategy. Man, this has been so awesome. Thank y'all so much.
Jon Orr: No problem, no problem. We're glad that you've got your next step ready to go, even ready for tomorrow. And that's something that Kyle and I constantly think about is what model or what strategy can we highlight here before we jump into that algorithm. So moving into geometry, moving into measurement, also take that same approach. How can I hold back on the main strategy first and then think about what can help my students kind of move towards that? So Megan, sounds like you've got some great next steps for you and we want to thank you for joining us here and if you'd have us, we'd love to have you back. Let's say, ooh, maybe near-
Kyle Pearce: Tomorrow.`.
Jon Orr: Yeah.
Kyle Pearce: No.
Jon Orr: Maybe near the end of the school year and we can hear some more successes and some more pebbles. What do you say about that?
Megan Garner: Yes, yes, yes. That would be amazing.
Jon Orr: Awesome.
Kyle Pearce: Awesome. That's fantastic. Megan. It's been a pleasure having you on. And again, we don't say it enough, but to our Math Mentoring Moment guests to be vulnerable and come in with a pebble and to chat about it because so many people, again, listen, we get so many emails, comments, things like that where people say, wow, I was struggling with that same issue. I'm so happy that someone was brave enough to come on and share it with the world. So thank you on behalf of the Math Moment Maker community and hey, we're wishing you all the best. Let us know how things go. Super curious to see if that helps you take one step in the right direction or continue in that direction, I should say, towards that magic wand waving classroom that we were describing earlier.
Megan Garner: Awesome. Thank you. Thank you.
Jon Orr: All right, take care.
Kyle Pearce: All right, have a great night. We'll chat soon.
Megan Garner: Thanks. Bye.
Kyle Pearce: Well, as always, both Jon and I learned so much from the Math Mentoring Moment episodes like this one here. We love just digging in to some of these challenges. And as Jim Strachan says, it's like whether that's just a tiny little bead of sand, one of those little tiny grains of sand, or whether it's a massive boulder, it's great to be able to have a conversation with folks just like you becoming vulnerable and really just trying to get it out there. Oftentimes just chatting about it can allow people to sort of almost emerge their own next steps in order to grapple with this challenge that they might have in front of them. So hopefully you learn something here today and hey, where are you going to write it down? Are you going to tell a neighbor, are you going to leave us a comment on YouTube? Are you going to maybe leave us a rating in review on Apple Podcasts? A rating and a review is a great spot for you to give us some feedback and let us know what you learned from this episode here today.
Jon Orr: Yeah, maybe they're going to be jumping over to our free private Facebook group, Math Mo Makers K to 12, or maybe hit the blog, which is the make mathmoments.com and check out some of the posts over there, or maybe Kyle, they will flip the switch here and join us for a math moment maker episode themselves. Remember that we only have episodes like this because of folks like Megan here who've reached out to us and asked for a conversation on her pebble. And you can also do that as well. Just fill out a little form here as one question. Tell us a little bit about what pebble you have. Talking about that pebble can often dislodge it in your classroom, make a world of difference, but also make a world of difference for other teachers who are going through that exact same pebble. So head on over to makemathmoments.com/mentor. That's makemathmoments.com/mentor. Fill out the form and we'll have a chat.
Kyle Pearce: I love it. I love it. Hey, show notes, links to resources and full transcripts, including I tucked in a couple links in these show notes. A couple division units that we have. One's called Sewing Seeds, the others called Niagara Falls. They involve division. They also share strategies and models, one of which is the area or array model that we shared or highlighted in this episode. So those are tucked away in the resources over at makemathmoments.com/episode215. Alternatively, if you just hit the makemathmoments.com site, hit podcasts and you'll see the episodes listed there. Give it a click and you'll be at the resource page. Well, until next time, my math moment maker friends, I am Kyle Pierce.
Jon Orr: And I'm Jon Orr.
Kyle Pearce: High fives for us.
Jon Orr: And a high five for you.
Sign up to receive email updates
Enter your name and email address below and we'll send you periodic updates about the podcast.
DOWNLOAD THE MAKE MATH MOMENTS FROM A DISTANCE CHEAT SHEETS
Download the Cheat Sheets in PDF form so you can effectively run problem based lessons from a distance!
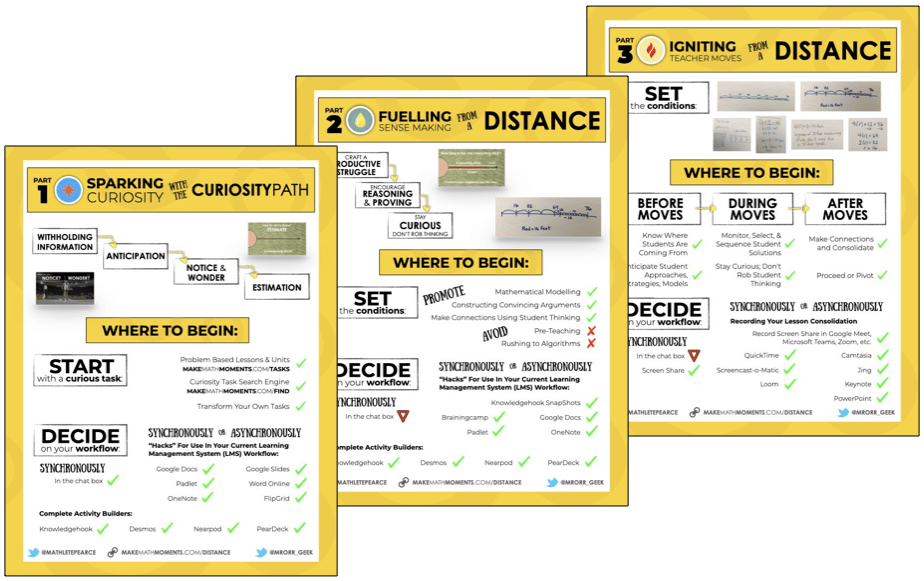
UP YOUR DISTANCE LEARNING GAME IN THE ACADEMY
There is a LOT to know, understand, and do to Make Math Moments From a Distance.
That’s why so many Math Moment Makers like YOU have joined the Academy for a month ON US!
You heard right: 30 days on us and you can cancel anytime. Dive into our distance learning course now…
Thanks For Listening
- Apply for a Math Mentoring Moment
- Leave a note in the comment section below.
- Share this show on Twitter, or Facebook.
To help out the show:
- Leave an honest review on iTunes. Your ratings and reviews really help and we read each one.
- Subscribe on iTunes, Google Play, and Spotify.
ONLINE WORKSHOP REGISTRATION
Pedagogically aligned for teachers of K through Grade 12 with content specific examples from Grades 3 through Grade 10.
In our self-paced, 12-week Online Workshop, you'll learn how to craft new and transform your current lessons to Spark Curiosity, Fuel Sense Making, and Ignite Your Teacher Moves to promote resilient problem solvers.


0 Comments