Episode #167: Decluttering Proportional Relationships – An Interview With James Tanton & Ted Coe
LISTEN NOW…
WATCH NOW…
James and Ted hop on the show today to dig into the collective work of a group of mathematics education leaders involving one of the most important yet misunderstood concepts in mathematics: Proportional Relationships.
Stick around as we dig into ideas around proportionality and what we can do to help declutter this crucial middle school math concept.
You’ll Learn
- How so much of the mathematics we explore in school is cluttered and what we can do to declutter your proportional relationship unit;
- How math is not just about the act of doing, but also the act of thinking and habits of thinking;
- About James’ fascination with emu eggs;
- Why you want to start with the most difficult problem first; and,
- Why we should be thinking about the words we use and say in math class.

FULL TRANSCRIPT
James Tanton: I feel like we've got so much clutter in the K through 12 world, and I think proportional reasoning is being particularly clutter-fied when it really is a beautiful chance to just teach students the confidence to rely on their wits and common sense, their thinking as we'd be saying all along. It's a beautiful example of that. It's absolute, absolutely cluttered with jargon, rate, unit rate, rate scale. I don't know, this goes on and on, on. Just common sense. Great chance to use your common sense. So that actually makes me quite angry and sad that we've taken away a beautiful story by making this three-year experience, at least in the US grade six, seven and eight, chapters that go on and on for something that is really just a beautiful chance to engage in common sense thinking. crosstalk
Jon Orr: In this episode, We speak with James Tanton, mathematician at large for the Mathematical Association of America and founder of the Global Math Project. And we're also talking with Ted Coe and WEA's director of content advocacy and design.
Kyle Pearce: James and Ted hop on the show today to dig into the collective work of a group of mathematics education leaders that I actually had the pleasure of being involved with on one of the most important yet misunderstood concepts in mathematics, education and friends, you know we've talked about this idea so much, we've done so much learning for so long on the idea of proportional relationships. Make sure that you're sticking around with us as we dig into these ideas around proportionality and what we can do to help declutter this crucial middle school math concept. Here we go. Welcome to the Making Math Moments That Matter podcast. I'm Kyle Pearce.
Jon Orr: And I'm Jon Ore. We are from makingmathmoments.com and together.
Kyle Pearce: With you, the community of Math Moment Makers worldwide who want to build and deliver math lessons, that spark curiosity.
Jon Orr: Fuel sense making.
Kyle Pearce: And ignite your teacher moves. My friends, Math Moment Makers, we are so excited to welcome on two awesome, awesome math educators from ... that inspire all over the place here. We've got James returning. This is his third time on the episode. He claims it's only two and a half though, because he's joined today with Ted Coe, one of our colleagues and a co-presenter that I've had the pleasure of presenting with on this concept of proportional relationships. We're so excited to dive into this concept, to get into the muddy waters and start to declutter. Jon, what are your thoughts here as we enter this episode?
Jon Orr: Yeah, it was a great conversation, lots to take away. I especially love this idea of the decluttering mathematics. James explains it so well, and I can't wait for you to hear it, so hey, let's get right to it.
Kyle Pearce: Here we go. Hey, hey there, James and Ted, thanks for joining us here on the Making Math Moments That Matter podcast, it's been a long time coming, but maybe not so long for half of you. I mean, James, I think you are now going to be taken the crown for the third time, but you'd like to argue because Ted's with you. It's only two and a half times. How are you both my friends?
James Tanton: So Ted, how are we both doing? You answer that question.
Ted Coe: I'm doing fantastically well. How about you, James?
James Tanton: All is good and grand here in sunny, Arizona well, it's evening now so the sun's going down, but beautiful, warm, sunny Arizona in the middle of winter. Yes, all is good.
Jon Orr: Yeah, he's rubbing it in, we're always jealous about these warm weather guests who come on here and flaunt this hotness in front of our cold spaces here, up here in Canada.
James Tanton: Shameless, I am.
Jon Orr: Awesome stuff, guys. We've chatted with James on the podcast, oh, back in episode six, which is one of the first and episode 45. Ted, why don't you fill us in a little bit and tell us a bit of your backstory. If you're a listener right now and you're like, "Wait a minute, why'd you just skip past James?" Hey, take a moment. Go and listen to episode six, go and listen to episode 45, get yourself filled in. Then come on back to us. Ted's going to fill us in on what's your role in education? How long have you been in the field of education and what's that journey looked like for you? Oh,
Ted Coe: Well, thanks for having me on the show. I'm excited about this. Again, I've been playing in this math education game for over 25 years now. I started off as a high school math teacher and loved that. It was just a highlight of a career. From there, I went to work in the community college system and the Maricopa Community College is in the Phoenix area. I was a math professor there, the chair at two different colleges. I even did little time as an assistant dean at a university.
Prior to where I'm at now, which I'll get to, but then I went over to Achieve, which was a Washington DC based education policy reform organization. I was a director of mathematics air for a while and I got to see things happening all around the country, the continent. It was just fantastic. And for the past year and a half, almost two years now, I'm the director of content, advocacy and design at NWEA based in Portland where I get to, just like my title says, advocate for content. And it's just a great thing to do. So that's how I got to where I am, the kinds of experiences that I've had along the way. We'll talk about more is that hour goes on. I'm sure.
Kyle Pearce: I love it. It's interesting because I actually didn't realize, but in this moment, I'm now realizing you and James have almost the opposite, you're like inverse experiences, where if I recall from episode six and episode 45, James, you began more in that post-secondary world and then came into the secondary world, if I recall correctly and Ted the opposite.
James Tanton: Absolutely, just call me an inverse kind of guy. Absolutely, I do things backwards all the time, yes.
Ted Coe: But James, you and I first met, I always had Achieve, and you were with MAA still at that point and you were just moving. Our offices in DC were a couple of blocks from each other and then you end up moving to Phoenix and now we live just more than a few blocks from each other.
James Tanton: What can we say? The whole destiny thing's going on here?
Jon Orr: Yeah, is destined to be close to each other.
Kyle Pearce: Actually, I do need to know this, because I didn't ask you before we hit record. But last time we all presented together, you two gentlemen were doing magic tricks where Ted's arm would show up on James's camera and really freaking people out, which, is that possible here today? Or is that not a possibility given ...
Ted Coe: My arm is not two or three miles long.
Kyle Pearce: Oh, look at that.
James Tanton: I can only do a one screen version?
Kyle Pearce: I love it, that's fantastic. Once again, promoting why you should be watching this on YouTube, my friends. James just did a magic trick and you only get to see if you go check out the YouTube channel. All right. Let's keep moving this thing along here, my friends. Sorry, James. We're going to spend a little more time with Ted here because we are going to flip this one to Ted. We always ask our guests about their math moments and my friends, definitely go back, check out James' math moments. But Ted, I'm curious, when you hear math class, what sort of math moment pops into your mind that you might be willing to share with the audience today?
Ted Coe: Well, obviously lots. There's lots of experiences pop in ... Let me go back to maybe the earliest that was perhaps a bit formative in my space. That was an episode in eighth grade. I went to a smaller school, where there was one class per grade and we were learning eighth grade math and we were doing something, I don't remember what it was, I think it was dividing fractions.
Kyle Pearce: Favorite topic of most young children.
Ted Coe: There was a worksheet and they taught me how to divide the fractions. And I had thought that I come up with a better way to do it. I'll put a little thinking into it. "Well, this is clever. I'm going to do this." And I proceeded to get all of them wrong on that worksheet. Then not only was that humiliating enough, but then I had to stay in during recess to fix it. So it's like, well, that's an interesting consequence for trying to be creative with your mathematics and the push back or the correction wasn't to talk through what was cool about what I was doing or not cool about what I was doing, it wasn't about the thinking that went into it. It was about, "Well, you're doing it wrong and so go do it right." It ties into my framing that whenever I talk about mathematics, teaching and learning in sort of a situation where anybody will listen to me, I say after all this time that I've spent in this business and in this world, I like to point back to three things that need to be a part of math, teaching and learning.
And one is that we do have the ways of doing right. We do care about ways of doing in mathematics, but we really care about ways of thinking. The ways of thinking are the things that really undergird all of that and keep it from becoming this scattered collection of mishmash, memorize as much as you possibly can. So in my eighth grade experience, there wasn't anything about ways of thinking. It was just ways of doing, but we got ways of doing, we got ways of thinking, and then the finally, I put in there as habits of thinking. So if we just settle for the ways of doing, then we're going to end up in situations where we don't recognize where the math actually exists.
A case, something I'll often use is I'll give an example and I'll ask adults, "When have you ever actually done division of fractions in real life? In a real life situation?" As you hear things back, it's kind of like, you know actually, that's not a division of fractions. That's more like multiplying by one half or something like that. I go, "Well, why do you think that is?" It's because you were taught division of fractions as strictly a way of doing disconnected from ways of thinking, so you never had the opportunity to see where it actually connects back in real life. You're going to hear more about this as we talk today, right? James is nodding. The ways of doing ways of thinking and habits of thinking are what we want to constantly bring back to the table when we're talking about mathematics.
Jon Orr: Yeah, so true. Sometimes I like to think about the progression or evolution of a teacher's journey. When you talk about that math moment, I always think ... and you brought up how that influences your teaching now. But we have so many new teachers listening to this podcast and I wonder what that ... right out of the gate, when you went to become a high school teacher, was it like, "I have this math moment that I remembered and I got to change math instruction?" Or is this like a gradual discovery that you were like, "You know what? This is the way math education needs to be." And it was a change for you. I'm always interested in this change or where this happened because I was a math teacher who taught math the way I was taught for many years. I didn't have coming out of the gate going, "I'm going to revolutionize everything." I was a very traditional teacher and it took me years to figure out what you have just said. But I'm curious about your journey there.
Ted Coe: Very similar, out the gate as a young high school teacher, I didn't see it quite this way yet. Maybe one of the most pivotal moments for me, if I can have another math moment. Is that all right? Can I have two?
Jon Orr: Yeah, sure.
Kyle Pearce: Yeah. But that means that James gets another one next then, okay? I think it's only fair.
Ted Coe: James gets another, all right. So another math moment though, was where my friend, who was the physics teacher in the high school, while I was the calculus teacher, he had fun. He was able to get minds thinking and engaging and they got to ...
Kyle Pearce: Because they do math with units, they would say, right?
Ted Coe: They got to think about quantities, right. And units and things like that. I'm like, "I'm going to make my classroom more of a place where the mind is engaged and where we're thinking about these things and we're making sense of things." Now that said, I read Peter Liljedahl's book recently. My takeaway was, I wish I had seen like this stuff earlier in my career and it wouldn't have taken me 15 years to get close to it, to try to figure it out on my own.
Kyle Pearce: I love that. Like Jon was mentioning as well, yeah, we're always curious about that. And I think for many educators, it's a process and we're on this journey and we continue on this journey. So the question for you James, is maybe not necessarily a math moment, but I wonder, is there something more recently that, maybe it's a new revelation, a new thought or a new, maybe something that you bumped into that you'd like to share? I know I'm putting you on the spot here, because we said, "We're going to skip right over James at this part." But what are you thinking?
James Tanton: So let's see, so I'm actually doing some work for a particular company somewhere in the world. I shan't mention countries and all the rest, but I'm looking at their curriculum. They've asked me, James, "Can you please make some videos to support this curriculum and make it human?" Which is an interesting charge, they actually used the word human. So I look at the materials and I have to say, I agree. They're somewhat inhuman right now. So, it's 11th grade high school mathematics and one of my jobs is to actually look at some of exams that are given out by this particular state slash province, slash canton, I'm not going to say what. I looked at these exams recently and I was truly horrified. I mean, this is something like from 40 years ago. It's like Ted's experience, divide these fractions. You're wrong when you get the correct answers but do a different method, unexpected, it's that level of work there.
Then I realized when I make these videos to support these new practice exams, I can actually talk about not so just much mathematics, but also the psychology behind this, what's really going on? It's not actually a matter of memorizing all the jargon and so forth. You can actually just use your common sense, take a deep breath, step back and figure out what do they mean by the terminal angle of the arm of an angle and standard position. I mean, there was some really whacko terminology that I as a professional mathematician had never used. But if you just sit back and think, "Okay, what's the context here? I'm doing trigonometry. What does everyone mean by the terminal point of an angle of an arm?" You realize well, we're doing unit circles, it must be, I don't know, where the star is at the end of an arm. Bingo.
So, I realized that a lot of my work is not so much teaching the mathematics, but teaching the confidence to rely on your own personal common sense, not to be ... Sorry, to have the agency to take charge of your own learning and doing, which is actually my greatest wish for the next generation, to actually teach the next generation the confidence to rely on their common sense, to be flexible in their thinking, to have self agency and to take action. Even in the most rigid of boring environments of a mathematics exam, still stuck from 40 decades ago of thinking, you can still find those moments.
So, my videos are now more like not just teaching the math and thinking behind the math and the habit of thinking, but also the meta analysis, you can actually say, "What's the author here want me to do apparently?" And I don't know this jargon, but I can figure out what they mean because common sense will tell me if I just give myself the permission to just think my way through it, on that level.
Jon Orr: Yeah, that's such a great realization moment because ... and something that I've been trying to stress in my students for so long and a couple episodes ago, we talked about the four pillars of starting a math class or getting kids into math class. And one of them is having that confidence to be creative. In so many of our math classes, that what I taught so long, it was like, "Thou shalt do it this way." We talk about, how many kids have ever heard the phrase ... or they were working at home with mom and dad and mom and dad might be showing them how to do math. But then the kid says, "But that's not the way the math teacher wants me to solve that problem." It's like, kids are all throwing their hands up and we say in our class, I want you to be creative. We want to hear your strategies before I say the teacher strategy. So, I'm glad you definitely brought that up. I know that's a big thing for me and the big thing that we all need to remember and emphasize.
James Tanton: And that what leads to a bit of a paradox box in terms of how mathematics is still perceived to this day. For example, we're all meant to teach the long subtraction now but many parents expect their kids in fourth grade, fifth grade whatever it is to do long subtraction, but they could ask someone, "Well, do you really expect a shop clerk when working out your change to go, '100.00 minus 9.87, carry the zeros, carry the ones,' do long subtraction to work at your change?" No, you want to teach them flexibility of thought. "I'll get three more cents to get into 9.90, 10 more cents gets me to $10. I owe you 13 cents." Now, I know that's not realistic example anymore because your cash register will do that for you. But my point is, there's a strange expectation what math is as perceived by the general populace. "You must do this with my child," whereas no one expects anyone in the real world to do it that way. Just as Ted was asking, when was the last time you actually divided a pair of fractures as a real practical need?
Kyle Pearce: It's coming back to even just this idea, and you had mentioned, you had used the term common sense. I use the word intuition a lot, like regardless of what term you use, it's like you're utilizing your experience and your thinking. Right there is that common theme that we've heard from everyone here is thinking. You're going to think about the problem and you're going to attack the problem based on what your gut, your intuition, your common sense is telling you is going to help you get to that answer versus going, "You know, wait a second, let's write this down." I always say 1,001 minus 999. I do that with parents a lot and I say like, "How would you subtract that?" Most parents say, "Well, it's two." Well, what did you actually do? And it's like, well, you know that the difference is two but-
Ted Coe: You thought about it, you didn't do it, right? That's the-
Kyle Pearce: Yes, exactly. And imagine if I said, "You're wrong." I was curious back with Ted's example, whether his creative approach was actually on track or was it way off track? Or my gut was suggesting that maybe the teacher was just like, "Just shut down this idea completely." Because no, it didn't look and sound like the way that they had thought it should be.
Ted Coe: It was probably flipping the wrong thing or something and trying to, but-
James Tanton: Could it be minus? Little tweak would've done it.
Kyle Pearce: Totally.
James Tanton: I know, there's this notion of showing your own work. I mean, it actually drives me bonkers. Show your work if it's interesting. I mean, if there's nothing to say about the work you did because the answer too, then just say two, but if the question's more interesting, then maybe you've something to explain, say it.
Jon Orr: Totally. Well, gentlemen, Kyle has talked, oh my ear off for the last few years, about this experience that he had a few years ago, he had gone down to Arizona and he went to this symposium on proportional relationships. I know the average listeners of the podcast know, that he and I talk about proportional reasoning all of the time. He had such fond memories and wanted to share so much of what he's learned there. I'm curious myself about that proportional relationship symposium. You had such a great group of educators, including yourselves. What inspired the formation of that group? And maybe take a moment to reflect on the thinking versus where you're thinking is currently on that group.
Ted Coe: Well, I think it started one night while I was helping my then middle school aged daughter with her math homework and we were doing something in her class, unit analysis, you string these things together and you cancel them out and so forth. I'm like, "Why are we doing this? Why are we doing this in this class?" Then I flipped and it said, "Oh, you're doing standard such and so we're on the proportional relationship standard." I'm like, "No, we're not." What? And then you dig into the textbook and you start to realize that they've taken all of this beautiful uniformity and unified thinking that goes into proportional relationships, and just broken it out and stuck this in there along with it, you're not thinking ... She wasn't being asked to think about changing units based on proportional relationships. It was just based on chopping out words and it was completely just totally out of bound, it was just completely without meaning.
Jon Orr: Is this like put the millimeters on top and the millimeters on the bottom and then just divide out and boom, you've got a new number?
Ted Coe: Boom, right. And it's like, "Well, where's the proportional thinking in it? Where is that?" So, when you say something is proportional, you got to be able to talk about what that means. I know that earlier, I had at one point in working with teachers and doing professional development, stopped and asked myself that question, what do I really mean when I talk about a proportional relationship? And had to go try to figure out what I, myself, how I myself would answer that. We started digging into standards and we started to see how you could misinterpret some of what's in there right now. It's set up for a really nice answer, but it's not necessarily clear right out the gate. It wasn't necessarily super clear either, in the progressions documents with regards to ... it was still disjointed, at least as much as I thought.
So, started to dig around, look into that curriculum and try to ... it's really hard to find curriculum that's handling this well. We were running the EQuIP reviews at Achieve and when I was there and trying to find exemplars of things, and we had a vacuum in that space, there wasn't a lot there. And so we started asking around and James, we looped you in at some point, there was a meeting with Dick Stanley at ASU somewhere along the line, where he gave a presentation, you and I rode out there together, and then ... How do you remember it from that point on?
James Tanton: Well, I mean, this all fits into my general mission. Obviously I'm a strange fellow here who wants to actually revolutionize the math education in the K through 12 world as we see it because I want to declutter everything. I feel like we've got so much clutter in the K through 12 world. I think proportional reasoning has been particularly clutter-fied when it really is a beautiful chance to just teach students the confidence to rely on their wits and common sense, their thinking, as we've been saying all along. It's a beautiful example of that. It is absolutely cluttered with jargon, rate, unit rate, constant rate scale. I don't know, this goes on and on. Just common sense, great chance to use your common sense. So that actually makes me quite angry and sad that we've taken away a beautiful story by making this three-year experience, at least in the US, grade six, seven and eight, chapters that go on and on for something that is really just a beautiful chance to engage in common sense thinking. And what a great meta lesson for the kids, engage in common sense and trust your fabulous wits. You've got wonderful brains, here's your chance to use them. So anger for me, is what came out of it, Ted.
Kyle Pearce: Well, and I remember quite vividly that the first time we all came together and listening to the conversation, the conversation initially, it was like we went down this rabbit hole of we started with, "Hey, what is a proportional relationship?" But then we went to, "What's a quantity?" And we went through all of these things and what I realized in that moment, and I can only speak for myself was, "Wow, I've never really thought about any of this." And that was from my secondary teacher background, I was new on this journey as a K to 12 math consultant and coach. That experience for me was a huge eye-opener of how much is going on and how much we don't think about. We talk about intentionality a lot on the show now. Back then, what that taught me anyway was that, wow, I say and do a lot of things in my math class that I don't even know if I have clarity around and yet I'm using these terms interchangeably at times.
Of course, we could dive into proportional relationships and all of those terms that are directly related to proportional relationships as well, when I'm like, "Wow, I actually don't have a clear differentiator." The one for proportional relationships that pops in is listening to people, try to define what a ratio is versus what a rate is. Different parts of the world have very different views on that as well.
So for me, that was such a huge eye-opener and it got me thinking, and I continue to think about a lot of these ideas and how so much of the elementary math we do connects to this work we do in proportional relationships, proportional reasoning, and so on and so forth. So I'm wondering, for you two gentlemen, what is a proportional relationship to you and has that evolved since that meeting, or maybe since before that meeting? How has your own personal journeys with proportional relationships grown over time?
Ted Coe: We didn't leave that meeting with everything locked up, not at all.
Jon Orr: You didn't solve all the world's problems?
Ted Coe: We didn't know and nor is there ever going to be complete agreement on it? And Kyle, I don't know if you remember, but I seem to recall, even in the first few minutes of that symposium, it was like a lot of folks didn't seem to think there might even be a problem, but about 15, 20 minutes in all of a sudden we were like, "Oh yeah, we're all talking about different things here."
Kyle Pearce: Absolutely and I'll be honest because I only really knew James at that point, James invited me into this world. So, I just sat and was an observer. I was like, "I'm going to just stay quiet on this one." Because you could see that there was some heels getting dug in and you could see how that would be true, especially for people who their life's work is mathematics and whether they had thought about it deeply, or maybe it just hadn't occurred to them. You could see how people were at very different places in their own understanding.
Ted Coe: Yeah. And then even in post that meeting, we all got together again, a few of us got together again, Phil Darro, April Strom, Dick Stanley, to continue to try to chisel down how we might talk about and present this in a way that makes mathematical sense and pedagogical sense at the same time.
Kyle Pearce: And James, you're thinking?
Jon Orr: He's been quiet over there.
James Tanton: Well, you just saw me go fetch something from my cabinet to my right. So, I'll explain what I fetched in just a moment.
Jon Orr: Looked like an avocado.
James Tanton: It does look like an avocado, but it's not, could be related.
Kyle Pearce: It's an emu egg.
James Tanton: You bet it is. Oh, inaudible it's an emu egg.
Kyle Pearce: Knew it, knew it.
James Tanton: Of course Kyle knew it was an emu egg. Every cool Canadians knows what an emu egg looks like. So, let's see, so has my thinking changed? So I hadn't thought deeply about this topic in the sense that I've really focused, at least my K through 12 board chiefly on high school mathematics, so proportional reasoning hasn't really come up as a core topic, it tends to be the middle school in the US, starting grade five grade six, going up to about grade eight. Only place it really came up for me as a high school teacher when I was teaching high school was the formula Y equals K X is considered a representative proportional relationship, and then off we go, because algebra's under the belt and there's no intuition behind it.
So, it was only with this thinking that Ted brought me into that really made me think, "Okay, let me do my usual Tanton thing." Let's try to strip away all the clutter. What's the kernel of the idea that's really going on here? Those sorts of things, year long processes that takes a long while to really cut down. But what is the key story? I will tell you, I think the key story is really not much to be honest, which sounds very insulting, but here's what I mean. I mean, I'll take the standard textbook problem, which says, suppose I figure out I can make 10 ... let's make it 33 omelets with 10 emu eggs. So here's an emu egg and I recognize I can make 33 omelets for 10 of these emu eggs. Great. Then the natural question you might ask and a textbook is, "Well, how many omelets can I make with 20 eggs eggs or 100 emu eggs? If I want to make seven omelets, how many emu eggs do I need?"
You realize, okay, there's the textbook question, so the culmination of all the theory that you should go through six graders, seventh graders with, and you think about it, okay what's going on? I've just given you a scenario. There's emu eggs and there's omelets, we counted emu eggs and we counted of omelets. So, there's two quantities going on and qualities could change. I can imagine they change. I can change the number of emu eggs, I can change the number of omelets, so things can change. In fact, that doesn't changing independently of each other, they're linked. I mean, if I changed number of emu eggs I used, I would change the number omelets I can make and vice versa. So, there's two link quantities.
So once I realized that I say, "Hang on, common sense tells me, my real world experience, something more going on." They're linked in a very nice way. I've said it already, so with 10 emu eggs, I can make 33 omelets. If I double the number of emu eggs, I bet I can make double the number of omelets, common sense tells me that. 66 omelets. Or if I half the number of emu eggs, I bet I can half the number omelets I can make. Here's math, I can't do that. So, that's 16 and a half omelets now. Or if I quadruple the number eggs I use, I'll quadruple the number of omelets I make. They're scaling in a very nice way. If I scale one quantity up by some factor K, whatever that number is, the other quantity has to scale as well. They're linked by scaling and tandem, I like to call it, and that's it. That's it. There is a proportional relationship, proportional reasoning.
In fact, the reasoning goes now, suppose I want to change the number of omelets I make. Well, let's think. 10 emu eggs, 33 omelets. 20 emu eggs, so double, 66 omelets. If I quintuple now, 100 emu eggs, five times 66, that's 330, I think, omelets. 100 emu eggs, 330 omelets. Oh, let's bring it down to one emu egg. One emu egg would be divided by 100, 3.3 omelets. Oh one emu egg makes 3.3 omelets. Oh, let me go to high school math like I did as high school teacher. What if I scaled by a factor N, N the emu eggs, I increase the number of emu eggs by a factor of N, the number of omelets I make increases by factor of N as well. So, N times one emu eggs, N emu eggs, makes 3.3 times N omelets. There's my formula. So, whoa, that's it. I can answer any question you want about number of omelets I can make, how many eggs I'll need, or how many eggs I've got, how many omelets can I make? Every standard textbook questions is now just there by common sense.
The young students can do this. My high school students could do this. I don't even need to mention rate, unit rate, ratio. In fact, I've used none of those words, common sense solves everything a textbook asks you of that question that right there.
I mean, so the point was, we stripped it down. You just need a real world scenario with two quantities that you can measure, that you can imagine these quantities can change in their measurements, how the base can change, inaudible can change. And they're linked in a very nice way, that they scale in tandem. Triple one quantity, the other one triples as well. Scale one by a fifth, the other one scales down by a fifth as well. Bingo. And then common sense will lead you through anything you might want to go about those two quantities, done.
Kyle Pearce: Well, and I love ... and the scaling in tandem, by the way, which we were joking over many of our symposium meetings, we called it scaling in Tanton, but either way, you know what though? We use that terminology in so many of our Math Moments units now, that I've had this experience over these past few years, and you'd have to remind me, was it 2018 when we began these meetings, maybe it was '17? I'm trying to remember.
Jon Orr: I think it was before that, yeah.
Kyle Pearce: Yeah. So whatever it was, that really has influenced, especially when I'm working with educators, working with younger students. So I know that our work was in the middle grades, working into secondary. We realized that high school students oftentimes didn't have this fundamental flexibility. It was like, again, they weren't given the opportunity to use their intuition. They weren't given the opportunity to use common sense when it came to proportionality.
What I see when we're working with younger students is this difference between additive thinking and multiplicative thinking. So James, you were highlighting this doubling, this halving, tripling, thirding, there's students where when you see them entering into this world, and they're stuck adding eggs and adding omelets or subtracting, you can clearly identify-
Jon Orr: "Well, every time I add an egg, I add 33 omelets."
Kyle Pearce: Right and it's like they're attempting to scale in Tanton but they're not there yet, but I'm thinking of from a teacher move perspective, if teachers are aware of this, they can be identifying that and they can be formatively assessing, as students are doing this thinking and doing this work to help them along and maybe select different quantities that might make it a little bit more attainable for them. So, instead of 10 and 33, maybe our quantities are two and three, whatever that number might be, that's going to help students move along that journey.
James Tanton: May I point out a potential danger then that actually just reinforces the worry you have. So I see in curriculum all the time that we insist that students make tables of data, one emu egg, two emu eggs, three emu eggs, so on. And then you see you're forcing students to think additively right then and there. "I add an egg, add an egg." The consequence of proportional reasoning is that actually the count of omelets I've got inaudible as well. But that is a consequence what the true story's about. You notice I didn't actually go to one egg, two eggs, I went 33. Then I went to 66, I went to 100, I went down to five. I went all over the place as the natural human brain does. I don't organize it in a natural way.
And yes, you can find consequences like that. Additive thinking does occur, but distracts from the story and if the students are still struggling between additive thinking, and multiplicable thinking, you're just inaudible some additive thinking to muddy the stories so they have multiplicable thinking. I say don't, I mean, actually don't do organized tables. I mean sure, organize your work in a nice row if like, but you don't have to do one egg, two eggs, this. Do 10 eggs, do five eggs, then do 20 eggs and do 100 eggs.
Jon Orr: James, a lot of the visuals that we've been putting together with our problem-based lessons is when we scale in tandem, we show a number of line or a double number line. What are your thoughts on showing and organizing your thinking along a number line to show ... because the table, I agree with you in the table, that the sense when you just start stacking them, there's no actual ... like I'm trying to capitalize on the physical distance sometimes when we're looking at numbers.
Ted Coe: Spatial magnitude, right?
Jon Orr: Yeah, spatial, exactly. And when you just put numbers in a table, you don't see that or feel it. But when you put them along a number line, I feel like you can see when I double this, all of a sudden I have to double this, but if I go up by three and that's not double, then it's a little bit more clear to see when I'm doubling and when I'm adding.
James Tanton: Oh. So I'll give my response and I'll stop talking as Ted should be really shining here, but I like the double you're showing on the screen right now because that's an actual double line that's in the context of the problem. You're showing a stack of books and you're seeing how the heights changes side by side. What I worry about is we make it an abstract notion of a double number line, most textbooks do, they'll draw a whole set of one, another whole set of one. It's not at all obvious why things should always keep lining up because you're actually relying on yet another proportional relationship that distances from the origin, scale and tandem. They're having to match the scaling in tandem that goes on from your physical scenario. It's a double layer of abstraction, it's not obvious.
So, what I love about what you are doing is keep the double number lines true to the problem that you're dealing with right now. Then it's like, "Well ... common sense." Now I can see what's going on. I can see adding three books is not doubling. I mean, going from five books to 10 books by adding five books is not the right thinking here. Well actually, it kind of is.
Ted Coe: Totally agree with you there, James. I was thinking, yeah, the double number line without any sort of quantities or relationships of the quantities, or thinking about why the quantities behave the way they do is just becoming another way of doing.
Kyle Pearce: You know what too, I think as well, it's like I'm seeing this concrete to abstraction continuum, I'm not suggesting that we move along it and never go back concrete or anything like that. But it's making sure that they're not proceduralizing the model too quickly. So, they look at this double number line, they look at a table like you were saying there, James. And it's almost like, "Oh, I see table. I do this." Versus, "I actually created this model because it actually helped me with my thinking." Or it helped me model my thinking so someone else can understand it. And that for me is a huge a-ha as well, is that I realized that even when I was using math models in my own classroom, I tended to try to teach kids, "Here's what you do." When you see this, you use this model and this is where you go versus letting the thinking take you.
I really like your idea of you had created essentially a table, you created a ratio table with your emu eggs, but you just did it in what we call a nontraditional, intuitive sort of way and it's going to look maybe out of order and it's going to look maybe messy. But you think about everything in the world and we talk about this a lot on the podcast now, that how come math class is the only place where we don't promote doing work and doing all your thinking and then making a better final copy later? An essay never starts as an essay, it starts as a jumbled mess of ideas all over a page. That's what math class should probably look a whole lot like too and then we can organize it and present it and share it with your math community. But I feel like we're always so concerned about students doing everything so neatly and organized and correctly the first time.
Ted Coe: One of the things, and if the listeners haven't seen the paper yet, that we're going to point to before the end of this, is we don't ever in this whole analysis, this whole approach, we don't ever set up and solve a proportion because that's not what we're getting at. Because we're trying to really build up that way of thinking about quantities that scale in tandem with each other in such a way that later on, that's fine, bring it in, bring in the way of doing. But right now, we want to make sure that your focusing on the way of thinking. The payoff is huge. I mean, we, we didn't even touch yet on percentages and how this just makes happy times of working with all the different kinds of percentage problems.
Kyle Pearce: Happy times, I love it, Jon, where are we heading next there? I got all distracted here.
Jon Orr: You've been throwing stuff up on the screen.
Kyle Pearce: I know, I'm getting all excited over here. I'm sharing all of kinds of visuals here. You know what? Let's talk a little bit more about that paper actually, and I'll bring it up. I'll put a visual up. We'll also include the link in the notes. Maybe we'll go back to you there, Ted. Through this work, we had been really trying to create some clarity. In our first presentation we had done a few years back, we used the word muddy, like the muddy waters, the muddiness of proportional relationships. Really what we're trying to do is create at least some sort of clarity, so that both educators and hopefully in turn students, have a better sense of what's going on and really bringing to light the beauty we're talking about, that is proportional relationships, instead of using the staircase for unit conversions or creating a ... or looking at ratios and always setting up a proportion and cross-multiplying or whatever the trick may be. Tell us a little bit about the paper and where we went with that paper and I'll pull it up and ensure we have the link in the show notes for those who want to dive in.
James Tanton: Okay, Ted just raised his eyebrows. Okay, so let's see. I mean, I think the paper ... What's the paper called? It's called Decluttering. Proportional Relationships Decluttered At Last. So, the mission is to declutter all that thinking. So, it really just starts off exactly how I started with my emu egg here. Can you recognize, you're in a scenario, it's a physical situation, has a two quantities that can be measured. The quantities can be varied or can be imagined to vary in the measures. And the two quantities are linked in some way that you change one, the other one has to change in reaction and vice versa and three, four, can't count, four that the key thing is are they actually scaling in tandem? Once you've got that, common sense will prevail. As Ted said, you always work from examples, like example if I tell you 80% of a quantity is equal to 120, your brain says, "80% of a quantity inaudible abstract. Well, I guess I'm talking about 80% of something and I'm also talking about 120 things, I guess."
I can now see my mind's eye I'm talking about two different quantities, a percentage amount and the actual quantity of whatever I'm measuring. And my brain says, "Oh, okay. If I half the percentage, I'll have half the amount. So 40% goes with 60. Oh, then I'm going to quarter that 10% goes with 15. Therefore 100% goes with 150." I mean, I'm just scaling in tandem right there. I recognize scaling in tandem in that situation right there.
Or taxes, for every dollar earned, I decide to give 43 cents to the government. In which case, if I earned $10, I guess I give 10 times 43 cents to the government. I guess this is just another situation of scaling in tandem. So, the paper's about really identifying that.
Then it goes through the language in the various ... Oh yeah, it's going through various scenarios. I was having fun with the paper here. Then what's the standard curriculum language? What does rate mean? Unit rate, ratios, all those. Draw these things about lines through the origin, all the stuff there. We just try to make sense of that. It really does fit with this just common sense thinking. Even the word scale. If I give you a map and I say the scale is one to 500 on the map and I see two trees on the map that are three centimeters apart. Oh, I guess scale means one centimeter on the map goes with 500 centimeters in real life. Therefore, three centimeters on the map goes with 1,500 centimeters in real life. I'm scaling with tandem. Again, common sense thinking in all those scenarios.
So, on screen right now, we're going through one long, long, long work example about buying Kewpie dolls before we've even done any curriculum work. You can just launch right into it like I did with emu eggs and omelets, you just follow your nose, all will fall into place. And then if you have to teach all the jargon and language, because you're in a situation you have to teach all the jargon and language, there's now context for it. It'll actually makes sense and nothing to memorize actually, because you always fall back on, "Well, I guess I have to answer this question, figure out what's going on here. If it's scaling in tandem, just muck my way through it. Things will fall into place, off we go."
But here's the lovely thing about this, is the chance to teach kids the competence of relying on common sense thinking. So, let me give you some scenarios that are quite questionable. I mean, if I tell you for example, it takes 22 minutes for seven socks on my mind to dry, how long will it take 14 socks to dry? Then you realize, well my real world experience is, well, it won't take double the amount of time for 14 socks to dry seven socks, they'll just all still dry in seven minutes, inaudible minutes. That's not scaling in tandem. So you have to rely on your actual common sense.
What's the danger, if you're thinking too hard, everything will go down the rabbit hole. If you're going to go into the line. Well, what do I mean by dry? What I mean by measurement of minutes? What I mean by this, this and this? Well, of course you'll go down the rabbit hole. At some point you got to rely on our own sense of the real world and how to make sense of that real world. Then you can start to become a physicist and say, "Well, what I mean by unit? What I mean by quantity?" When I say one yard is the same as three feet, actually, I guess I'm doing scouting and tandem again, I'm giving different names for units. Therefore two yards is the same as six feet and 60 yards is the same as ... times that by 30, whatever it was, feet. Off we go. All that unit conversion stuff actually is scaling in tandem again and there's really nothing new. It's just actually same one idea over and over again.
So to me, the point of the paper is it's the same one idea over and over and over again, over and over again. We do if for three years, the same one idea over and over again. And we never say what the actual idea is. So, we're saying it, that's what the point of the paper is.
Kyle Pearce: Well, and I love it because it's like we do it for three years, but I feel like we haven't been doing it for three years. We've been kind of doing some stuff, but again, going back to Ted's point doing the doing and taking these ideas and again, teaching them as siloed ideas. Today we're going to do unit conversions and it's like this whole other thing that we painted up and we say this big experience is going to be this whole thing you've never seen before. When in reality it's like, well actually, no, you've been doing all of this all along over here. And it's just such a beautiful way to make it connected and while it is big and it's massive, that is such a positive thing for the learner. To be able to say, "Wow, holy smokes. There's a lot that I can do all based on the same fundamental ideas."
I look at this paper as a really great opportunity for educators like myself, who three, four, five years ago, I was not necessarily doing a great job at understanding proportional relationships and how complex they are. Complex, but in a good way complex, because I could take that complexity and I could use that to make math class feel more intuitive. But it does force me to do a little bit of my own learning along the way as well.
Jon Orr: I feel like I'm seeing a couple things that teachers inaudible there's some nuance here that teachers, we want to make sure that I think hit home for them. What I mean is when I'm thinking back to my old self and teaching proportional reasoning in my say, ninth grade class, and I'm imagining the textbook and the textbook has ... Kyle, you call these naked problems, right? So, it's just they're context-less problems. They're just, you've got this fraction, you've got a proportion, you've got a fraction.
Kyle Pearce: There's no emu eggs.
Jon Orr: No, there's no eggs. So it's like, there's a fraction, there's other fraction. There's a missing value. One of those fractions, sometimes it's on the top, sometimes it's on the bottom and we cross-multiply to solve? It was like, there's this solving proportion section of the textbook, that always starts with naked problems. And then at the end, we put in context. So, what I'm hearing for you guys is ... because I don't think we ever physically said it is that if a teacher is like, "Look if I'm going to redesign my proportional unit, my proportional relations unit," in one of these grades and they're pulling from the textbook and the textbook is doing that. We're saying, "Hey, you got to start with context." Is that a no-brainer?
James Tanton: So, I'm going to be really, really bold. I mean, I'm going to say, sorry, so much of the equipment is designed nowadays, teach stuff kids that they need to know later on, which is not how the human brain works. Either do it when you need it later on or do the later on now. In fact, I'm going to offer do the later on now. I say-
Jon Orr: Go do the later on now, I like that.
James Tanton: Go to that hardest problem at the end of that textbook chapter and present that first and say, "What are we going to do?" Have a messy conversation that probably gets nowhere and that's okay and then just practice just trying stuff. Well, I guess we've got emu eggs. Let's just start saying the obvious things. We've got omelets. Start saying the obvious things and we just start listing things and you start having a conversation that goes from the obvious things to state, to the even more subtle things to start stating. I'll bet you'll start making some progress and then you'll start seeing the context of the things the chapter starts with. And then if you actually want to teach cross-multiplying, which I say ... Well, I've got my own personal thoughts about that, but at least you now have a context and a place for it. It's not a be all and end all. I mean, no one in their right mind would cross-multiply and you're not really cross-multiplying, I don't know what that means. You're multiply both sides by one number, then multiply both sides again by different number and you're just putting fractions on both sides. That's all you're really doing.
Kyle Pearce: Absolutely. And what I'm hearing as well, and then I want to flip to Ted and get your thoughts on this as well, I'm hearing this idea that it's really hard. It's really hard to use your common sense or your intuition when there's nothing to really be thinking about, unless you really ... If I really understand fractions, which most students tend to not really understand fractions by the same connection to proportional relationships, same downfalls that we've traditionally taught fractions and introduced fractions. But if there is some context, if there is something worth solving, then I can at least take that and I can use my background experience with that idea and use it to again, naturally work within proportional relationships. Ted, what are your thoughts there in terms of teachers are listening, they're going, "Okay, this seems awesome." Any tips? Any thoughts or wonders for our friends?
Ted Coe: Yeah. So, we often talk about meaningful mathematics discourse, having meaningful teaching practices, mathematical discourse, meaningful. You got to stop and ask, what does that mean? What does that mean? Well, you can't have meaningful mathematics discourse without focusing on mathematical meanings. You have to come back and you have to think about what it is, the thing that you are saying means. For too long, we all just said proportional relationships and we all assumed we meant the same thing. We quickly found out we did not all mean the same thing.
And so the question is now, well, what other places are there like that? You talked about fractions. So we've got one project that I'm working on right now, we're calling formative conversation starters. We're trying to get into how are students thinking about these things? And so we ask questions like, "Is a fraction one number or two numbers? Can you access ways of thinking that can make those things work in your head?" We ask you, "Hey, how do you think about division? What ways do you have to think about division?" Then let's ask you about division of fractions. Are your two answers different between those two things? What ways of thinking, what are the meanings that you're bringing to the table? That's where the meaningful mathematical discourse has to start.
Jon Orr: Totally. Gentlemen, we've had such a great time chatting about this and I know that we could probably keep going and we could probably fill another hour or however long. I definitely want to meet up with you guys in the future, as long as we can start to get together in physical, face-to-face environments and conferences. I can't wait for that to come about again, here in Canada. It hasn't happened yet. But before we say our goodbyes, I'm wondering for each of you, what big idea or takeaway would you want to leave with our listeners as a final thought?
Kyle Pearce: Yeah, let's start with James.
James Tanton: I like what we said earlier. Start with the hardest question at the end of the chapter at the beginning of the chapter with your kiddos. Do that, see how it goes.
Kyle Pearce: I like that, good tip.
Ted Coe: For me, it's slow down and ask yourself and your students, what do you mean when you say this? There's too many things that we assume that we all mean the same thing and we don't.
Kyle Pearce: I love it. And you know what? Hearing both of those things I think is going to be really helpful. I hope that friends who are listening to this episode, I know that they're going to take a lot away from it. But me personally, even just hearing both of you reiterate those two things, I think about it and Ted, you had just mentioned this idea of having these conversations and really again, the thinking emerges. As soon as, hey, you take that harder problem and you start with it thinking happens and hey, if we ask each other, "What do you mean when you say blank?" We have to do some thinking. And once again, I think that really drives home a huge idea, something that I know for many years, not enough thinking was happening in my own classroom and that's been a journey that I've been on for many years now, and I'll definitely take those two thoughts into the future and continue to work on this journey here.
So thank you both, gentlemen, for hanging out with us. It's awesome. I know it's only virtual these days. It seems like forever since we've all been together but again, like Jon says, crossing fingers that we are coming around the bend here. It has to be, we have to be, I don't know what else to say here. But thank you both for coming on the podcast, sharing your thoughts with the world as you always do. I'm sure we get you both on again the future. James, you might run away with it, right?
Jon Orr: He's got a record to keep going.
James Tanton: Right, okay, I'm going to work on it then. No, guys, thank you so much. A real honor, real pleasure. The work you're doing in the world is just tremendous, so thank you so much for all the good you're doing in that world, really touched to hear, so thank you.
Kyle Pearce: Agreed, thank you so much.
Jon Orr: Thank you, gentlemen, and have a great rest of your evening and we'll talk soon.
Kyle Pearce: Well, as always my friends, and you heard it, we are so excited to have welcomed James and Ted onto the show. We're definitely going to have to have both back on the show, maybe together, maybe apart, but one thing I must say is that with every episode I take away something new. I've had the opportunity to co-plan much of this work in proportional relationships and co-learn with these two individuals, as well as that symposium, that group of educators who joined us for the proportional relationship symposium. So my wonder to you is what is the new learning that you are taking way?
Today, one of the big themes I heard was thinking, it really came down to thinking. What we're doing in the classroom. Are we thinking about the math content that we're teaching? Do I fully understand the math content we're teaching? It's okay if you don't, but you need to be thinking about it and thinking about the intentionality and maybe have that discussion with your students. Make sure that you're doing something to reflect on that learning so that it sticks. So, create a plan for yourself to take action on something that you've learned here in this episode today.
Jon Orr: Right, and what you could be doing as well is reach out because you are not alone here. We have a vibrant community of Math Moment Makers here to support you. You can reach that group over on Twitter @makemathmoments, or on Instagram, or in our Facebook group, Math Moment Makers, K to 12. Get in over there, we've got lots of folks chatting and answering questions and assisting fellow educators, just like you.
Kyle Pearce: Yes. And my friends, if you weren't laughing, when James pulled out an actual emu egg and put it on the screen, that's because you're probably not watching this on YouTube. Head over to the YouTube channel, hit that subscribe button, hit the like button, leave us a comment. And remember, we have weekly videos being released with tips, tricks, and a little bit of guidance, a little bit of inspiration for you in your own math classroom. So, do us that huge solid, hit that subscribe button and let's make sure you see us over on YouTube.
Jon Orr: Yep, show notes and links to resources and complete transcripts from this episode can be found and downloaded over at makemathmoments.com/episode1R67.
Kyle Pearce: Well, my Math Moment maker friends until next time, I'm Kyle Pearce.
Jon Orr: And I'm Jon Orr.
Kyle Pearce: High fives for us.
Jon Orr: And hey, here's big high five for you.
Sign up to receive email updates
Enter your name and email address below and we'll send you periodic updates about the podcast.
DOWNLOAD THE MAKE MATH MOMENTS FROM A DISTANCE CHEAT SHEETS
Download the Cheat Sheets in PDF form so you can effectively run problem based lessons from a distance!
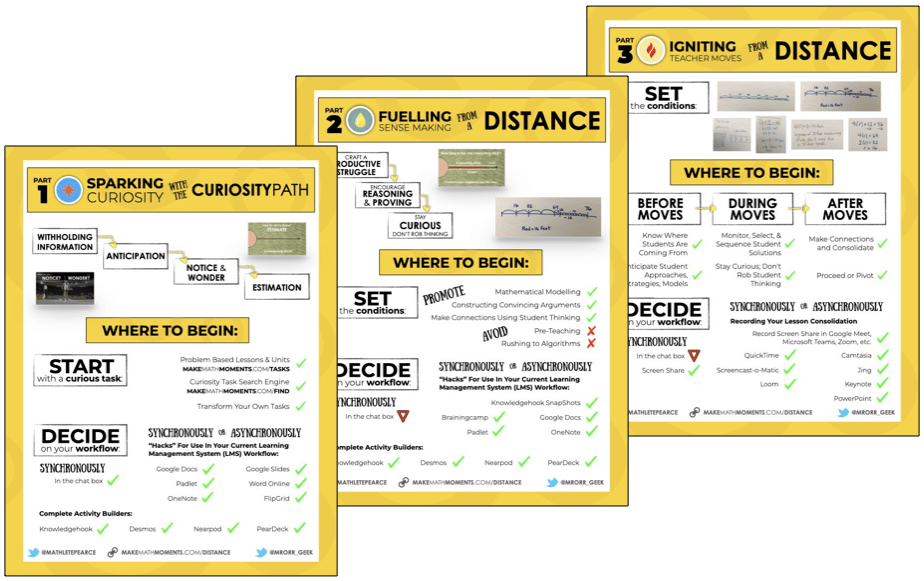
UP YOUR DISTANCE LEARNING GAME IN THE ACADEMY
There is a LOT to know, understand, and do to Make Math Moments From a Distance.
That’s why so many Math Moment Makers like YOU have joined the Academy for a month ON US!
You heard right: 30 days on us and you can cancel anytime. Dive into our distance learning course now…
Thanks For Listening
- Apply for a Math Mentoring Moment
- Leave a note in the comment section below.
- Share this show on Twitter, or Facebook.
To help out the show:
- Leave an honest review on iTunes. Your ratings and reviews really help and we read each one.
- Subscribe on iTunes, Google Play, and Spotify.
ONLINE WORKSHOP REGISTRATION
Pedagogically aligned for teachers of K through Grade 12 with content specific examples from Grades 3 through Grade 10.
In our self-paced, 12-week Online Workshop, you'll learn how to craft new and transform your current lessons to Spark Curiosity, Fuel Sense Making, and Ignite Your Teacher Moves to promote resilient problem solvers.


0 Comments
Trackbacks/Pingbacks