Episode #331: How Diverse Math Teaching Styles Help You & Your Students
LISTEN NOW HERE…
WATCH NOW…
Are you maximizing the strengths of your background when teaching mathematics, or could collaborating with educators who think differently unlock new possibilities for your math classroom?
Math instruction often falls into two camps —conceptual or procedural(The Math Wars). But what if the secret to reaching every student lies in combining these perspectives? This episode dives into how diverse teaching experiences can transform math education.
- Understand how connecting conceptual understanding to procedural fluency creates lasting math retention for students.
- Gain insights into the power of collaboration between educators with differing math backgrounds.
- Learn how to value and validate all students’ mathematical thinking while fostering equitable learning experiences.
Press play now to discover how embracing diverse teaching approaches can inspire growth for you and your students!
Attention District Math Leaders:
Not sure what matters most when designing math improvement plans? Take this assessment and get a free customized report: https://makemathmoments.com/grow/
Ready to design your math improvement plan with guidance, support and using structure? Learn how to follow our 4 stage process. https://growyourmathprogram.com
Looking to supplement your curriculum with problem based lessons and units? Make Math Moments Problem Based Lessons & Units
Be Our Next Podcast Guest!
Join as an Interview Guest or on a Mentoring Moment Call

Apply to be a Featured Interview Guest
Book a Mentoring Moment Coaching Call
Are You an Official Math Moment Maker?

FULL TRANSCRIPT
Yvette Lehman: Hey John, today we are going to talk about the two diverse experiences that math educators bring to the classroom. And I think that it’s actually perfect that you and I are doing this episode together because I think that we represent these two diverse experiences.
Jon Orr: Okay, what do mean diverse experiences? me the lowdown on what you’re meaning here.
Yvette Lehman: So I know that for you, are obviously a secondary math educator. you know, went through school to focus on math. Math was probably the subject that you excelled in. Right. And it was probably pretty easy for you. And you probably found that the way that math was taught worked for the most part. Like there’s a reason that you chose it as a career path.
Jon Orr: Right. Yeah. I was a memorizer. I was a memorizer and I got a lot of satisfaction of memorizing and then regurgitating. And it was like, I loved that part about math. It was like, I can follow this pattern. Because that’s what everything came down to for me. was like, I could follow this pattern quickly.
And then I could use that same pattern to solve this other pattern over here or this this problem over here. I was never a great problem solver. You know, I was always like, I can I can follow this this procedure, and I can then recreate that procedure over here. And I get a pat on the back when I do it right.
Yvette Lehman: Well, and I was the complete opposite. I always describe it’s like math was like mud to me. Like it’s like they might as well have just like smeared the entire chalkboard because none of it made sense at all. And I can’t memorize that way. It’s like if I, without meaning, it will not stick for me. And so I even remember being in elementary school and being taught the formula for area, which to me now is like such a simple concept.
But man, it’s like I could not remember it. And on top of that, I just wasn’t, I didn’t have any fluency. I had no operational sense. But then imagine, you know, we both end up becoming math teachers. So here, you’re secondary math and I taught mostly, you know, junior intermediate. So sixth, grade six and seven predominantly in the classroom. And yeah, go ahead.
Jon Orr: Right. Yeah. So I was just going to say like you, you’re highlighting our backgrounds, right? So it’s like, I came from the secondary. I have a math degree. you know, I went to all the school for math. you’re an element, you’re an elementary teacher. We’re both teaching math now, but, why, why does it matter? Like you, let’s talk about like the two dynamics here. Cause like everyone in different buildings has a version of this, right? You’ve got, you’ve got that math.
focused teacher, whether it’s in elementary and they’re teaching grade eight or grade seven, and they’re like, Yep, I’m the very procedural math teacher because I taught like that for a very long time, like my first 10 years, very procedural taught the way I was taught most of us did right, most of us do, except for you. And then, you know, you’ve got kind of that I follow the procedures, this is the be all and all is like, let’s make the procedure, the mimicking the getting it out, you know, that was what math was for us. And for me, and this is how I learned it.
What you’re, that’s, you know there are people in your buildings like that and they will stick to the, you know, math speed is a factor of math. Accuracy is the most important part of math. Getting the way to write it down this way is the most important part of like doing well in math class. But then you also got a, you know, teachers in your building like you who are coming at math from, I never understood it.
I’m really trying to understand the conceptual because I’ll admit, I was never bothered by the understanding of like why this worked and why that didn’t work. Like I never remember asking those questions when I was a student. So it’s like, you’ve got that experience coming in. Like I want to make sure everything makes sense for me so I can make it make sense for kids. And that’s a priority in your world.
which might not be the priority in that other teacher’s world or my world for their first 10 years. But what we’re saying, I think what you’re trying want to make here and what we want to talk about here is that we need both in a way. Like you need to kind of like, in a way have both, but like you need to rely, like each of those two different people need to rely on each other.
Yvette Lehman: exactly it John. It’s like we are a perfect match and people might be surprised to hear that, that like somebody like me who had you know a very let’s say challenging math experience as a student who now you and you summarized it perfectly. It’s like I cannot teach math without understanding it and so therefore I create an experience for my students that’s rooted in understanding. It’s like we’re gonna build it, we’re gonna see it, we’re gonna use context because if it doesn’t make sense there will be no retention for me and I imagine many of my students. But we’re, go ahead.
Jon Orr: Right. Now, I was going to say that that makes sense. Now, this is just because I’ve grown to know that these are important things to have in our classrooms. So when you think about it, and I think everyone listening right now is nodding their heads, being, I want that for my students in my classrooms. They’ve been striving towards having, creating sense making for their students in a different way than they’d learn math.
So why does it make sense that you should go and find someone who was like me as like an important part of your learning as a teacher?
Yvette Lehman: It’s a great question. at the end of the day, and I actually, you know, this is not my idea. This is from Cathy Fosnow and leveraging a lot of Cathy’s resources. But at the end of the day, after we’ve engaged in these rich tasks and we’ve made sense of mathematics and we’ve represented it and we’ve used context, we still have to formalize it. Like I still have, I’m the one, the teacher is the one who is responsible.
for connecting the mathematical representations. So I have to take what we did, what we acted out, what we drew, what we modeled, how the math behaved, and I’m the one that actually guides the students to the formal representation or the more procedural representation. And this goes back to the debate between conceptual and procedural. Of course, you and I both firmly believe you need both.
It’s not enough to just conceptualize math and it’s not enough to procedure, you know, do a procedure. The actual strength is in the connection of the two. But my problem is I actually, and maybe this is also my gift. Kyle actually used to joke with me all the time. My problem is I actually don’t know the procedure. I don’t know the rule or the trick. Like if you tell me…
Jon Orr: And I didn’t know the conceptual.
Yvette Lehman: Right. And so what I would often do is I would have to, particularly when I was in the classroom and even in other roles, it’s like I could make sense of something. So I would, you know, solve the problem in the ratio table or on the number line or in an array. But then I would go to somebody like you and I would say, OK, now, John, show me how to solve this algebraically, because I need to take my representation and match it to your algebraic thinking. And both pieces are really critical to support student understanding.
Jon Orr: Totally. In our opinion, and in the work that we’re trying to do, is that is the math that we want to learn, is that connection. is to say, we have the conceptual, we’re going to move towards the procedural fluency. Both are equally valid and not one is weighted more than the other. And I think when we think about conceptual understanding, if we’re in that, say, wanting that for our students, we put a lot of emphasis over there. And if I’m the very procedural teacher, I put all the emphasis over here.
But we want to make sure that there is that balance between the two. the power is connecting the two. That’s the teaching that has to happen. And that’s the learning, the outcomes, really, that we need to help students make. Because if you think about it, we can’t have students just always drawing this over here and taking, let’s say, a long route to get to a particular answer. We want them to get closer to that procedural.
the representation of the abstract representation because there’s power in the abstract representation that you can’t always have in the conceptual and vice versa is true as well. And it’s like, think of it, the history that math was developed was probably rooted in the conceptual anyway. And we moved it towards procedural because it allows us to move quickly. It allows us to like represent our thinking in very standardized ways that other people can represent, you know, see and understand and make sense of because they
also have that same standard of representation. Like there is power in say, going to this abstract representation, but very much power in the conceptual. So both need to be matched. And I think you’re right, like having it shown to you is allowing you to like make those connections. And this is the same that needs to be true for that person who’s, you know, very procedural. And I think a lot of us listening right now are
work with people who are very procedural. And we would love for them to have like this conceptual understanding. And then we want to make like, it would be great to have that person it’s like, hey, the two of us are going to kind of join forces and bounce different ideas off each other to see what are you doing conceptually? How do I link it to procedure? What are we doing procedural? How do I link it to conceptually? Like, I think there’s a lot of a lot of effort to go one route right now, because there’s a lot of procedural teachers out there.
Jon Orr: and we’re trying to bring the conceptual to them versus vice versa because more people have the procedural than the conceptual, I would think.
Yvette Lehman: So how do you develop the conceptual? I mean, so you’ve shared that that was part of your journey, right? Is that you started really strong procedural and you didn’t really have the understanding. So what worked for you?
Jon Orr: Mm-hmm. What were, yeah, what worked for me, think, I think was, it was specific PD trainings that allow, you know, allowed me to have say witness what this could look like when I, when I understand it and what my, students understand it. Like it’s not something that I just stumbled across because I actually used to gloss over it. I used to be the teacher and there’s a lot of teachers still like this is that the core resource that we were using.
You know, when they shifted, I was teaching, say, I think it was ninth grade, there was algebra tiles and area models all embedded in that core resource for multiplying binomials. And I used to skip over that and go, I’m just going to show them the right way to do it, because it’s quicker if I do it this way. to me, my philosophical approach back then was math was about getting to the standard algorithm, was like getting to this procedure so that we can do it.
and use it when we solving problems. So it’s like, well, why not just go right to it? I could show you clearly. And to me, teaching back then was about how fast could I get you to understand that or get you to follow that? Like if I can, if I can explain this very, very clearly and step by step, I was a really great teacher, right? Like that was my goal. And I think that’s still the goal of many, many teachers. So when I was put in positions of representing
that different in different ways or seeing the power of like it modeled well for me and I could see my own I got like a feeling of like I saw the like when it was clearly pointed out the connection between the say the area model and multiplying that’s when I’m like like that that’s we call that the math epiphany like it’s in a math epiphany where I’m like I did not know that that
thing that was in that core resource, that textbook that I used to skip over. That’s what we were talking about. Like I used to just think, what is that? It’s just like, and this is what teachers still say. Like that’s a tool for kids who can’t go quickly into the, to the algorithm, which is not, not the case. But when I felt it and I, and I felt that power of like, my gosh, like it doesn’t matter if I do it in this order. If I, it doesn’t matter if I draw it this way or you know, like you got the flexibility of this connection. When we teachers have say,
that, I guess, in a way, an emotional response to something, that epiphany, that’s when you usually switch from one side to the other, or you switch to saying, I’m now going to use this because I can’t unlearn it.
Yvette Lehman: and you know I’m going to be very honest I certainly didn’t come into the profession with conceptual understanding either I had neither so I had I didn’t have conceptual understanding and I didn’t have procedural fluency what I had was math anxiety you know and I’m just a negative I I had a poor sense of my own ability in mathematics but what I did have I guess the strength that I brought was recognizing
that I needed to do something different than what I had experienced. Like I just, knew that that wasn’t good enough for kids. And I knew that I would be leaving kids behind if I just followed the textbook and modeled and had them mimic. So my big moment was I attended a PDU, it was actually with Kyle at the time. And I learned about the math proficiencies and I’ve shared this before. And I walked away from that session, realizing that math was visual.
and that math could be seen and manipulated in your hands. And it wasn’t just this, you know, symbolic, confusing representation. And so for that first year, we made a commitment, my teaching partner and I, to represent every single concept concretely, everyone. And it’s like if we couldn’t represent it concretely, that meant we didn’t understand it and we had to seek outside consultation from somebody who did.
And that was like, we committed to ourselves and we committed to our students that in, and you know, evolved from there. Like I realized later that, you know, some concepts aren’t great concrete, you know, fractions for examples are better with pictorial. And so obviously my understanding of visual representations evolved over the next few years, but that commitment to ourselves and to our students that we would follow, you know, the concreteness fading model.
was the shift that I needed to build my own conceptual understanding, which then was almost like the catalyst for all of the change that I made in math instruction.
Jon Orr: And I think the important, like, regardless of like that impact that you had on yourself and your learning, I think the real, the real, you know, think about, think about what Yvette has just said. It’s like, I made a commitment to always doing this action. And that right there is, is, is like the gateway to like change in my, in my opinion, because I remember like, I’ve, I’ve said those words in different ways.
throughout my career and every time it made an impact like early in my career before I had that conceptual understanding like I remember someone handing me the TI calculator and it was like this new calculator is gonna be great for kids to explore you know how transformations work with with you know parabolas and quadratic functions and any type of functions because you know the TI inspire had like engaging techniques and I’m like that’s
That thing, it looks like it’s so confusing to use. And I remember saying like, I’m just going to commit every time I’m going to do something on a calculator, I’m going to use that calculator. And that was like my first couple of years of teaching. then it became normal. It became part of your routine. So that’s one example. I mean, every time I had a similar experience when I
when I realized the power of the number line for proportional reasoning and solving proportions. And I taught high school, right? So it was like, every time we are solving a proportion, I’m going to represent it in front of the students on a number line so that we can see how, say, the scaling works and see how the additive and multiplicative relationships exist on the, the number line.
And it was a commitment that I made to myself in my, know, to say, I’m gonna do it, which means I had to like know it before I could do it in front of my kids. And I had to feel confident that I knew what I was kind of thinking about and trying so that I could show the kids and explain it when we needed to explain it. But it’s like every time I know that I had that epiphany moment or that kind of shift in my teaching, it was when I said those words you just said, which is like, I’m gonna make a commitment to always do this. And I think.
Jon Orr: I think that is the huge kind of movement maker when it comes to educational growth.
Yvette Lehman: Yeah, and I think that, you know, kind of going back to the start of the conversation, that journey for me where I said to myself, you know, I’m going to commit to representing every single concept that helped me with my conceptual understanding, but it didn’t help my procedural fluency necessarily in a more, let’s say, formal or symbolic way. And that’s where I had to leverage the expertise of other people in my building. And I, you know, I remember vividly
I had had this epiphany, I was representing something either concretely or visually, and I knew that it worked and I trusted it I’d made generalizations, but I didn’t know how it would be taught formally or I didn’t know how to represent it symbolically or what the steps would be. So I remember going to a grade eight teacher in our school to basically say, okay, can you show me how you would solve this symbolically? And I needed that.
Like I needed that bridge between what I had conceptualized and understood and that formal. And we talked earlier about, has anybody ever, you can probably picture this person, you know, who again, strong math background, confident in their ability to teach math, very efficient, knows the procedures. Like I needed that person, but what that person maybe didn’t realize at the time is that they also needed me.
Like with, we’re talking about creating accessible experiences for all students, if we want to shift from being gatekeepers and saying only some students should have access to higher levels of math education, then, you know, I needed that grade eight teacher. I needed him to show me how to formalize this or, or represent it algebraically. But, you know, the time we spent during nutrition breaks, he probably didn’t realize he also needed me to show him symbolically or the visual.
Jon Orr: Right. Now, did that materialize into any you showing him or was it a one-sided kind of conversation? I can imagine.
Yvette Lehman: I mean, I think I probably benefited more. I probably benefited more. But even the fact that, you know, we always say anytime you do math with others, you know, taking time during your lunch break or during, you know, any prep period where you’re just literally standing side by side with another adult solving math problems is time well spent. Like there’s no more powerful professional development opportunity than just
solving math problems together and I think it’s even more powerful when you actually bring people who are coming from the opposite ends of this experience.
Jon Orr: Yvette, is that the big takeaway you want, you know, the listeners to take away today?
Yvette Lehman: I think so, yeah, for sure. We say this all the time, but we’re gonna be more specific today in the find your people. And don’t just find like-minded people or people that share the same experiences or strengths that you do, because that’s helpful. It’s helpful to find people who are going on the same journey that you are, but there’s actually tremendous value in finding the opposite person.
Jon Orr: It’s how we grow. I think you get tested. You get to test and get tested on the things that you have beliefs on, which are important pieces of growth. Before we hit record here, I guess it’s a quote or a phrase or a statement that I think…
hits home, you know, hits well here is that we should have strongly held beliefs, but loosely held, which is, which is like, I believe, I believe this to be, know, if I believe this to be true, then I strongly believe it. Like I, you know, if I, if I strongly believe that conceptual understanding is the gatekeeper to math understanding, then I’m going to be like, I’m all in, let’s do this. But then the mo and why we say loosely held is because the moment you have, you have new evidence that says maybe
this thing over here might be the better approach, then we should consider it. We should go, how does that blend with what I know to be true? How does that blend with my current understanding of this particular topic, particular idea, and does it hold any weight? And should I bring that into my thinking? Because that’s where we grow, is when we start to think about new ideas.
and how they influence the things that we already know to be true or untrue. We can be strong in our beliefs, but we need to be ready to be like, adjust if we have new evidence that presented. So, you know, that’s a growth mindset type of thinking. But you know, that teacher who is probably that teacher that you were talking with was strongly held beliefs, but strongly held. And that’s a scary thing to be, right? Is that I always believe this, and I’m…
never going to waiver, even when I’m presented with evidence that maybe this is a say an alternate strategy that can have more of an impact in say, whatever, you know, whatever, you know, fields we’re talking about, because this is not like that phrase isn’t just a math phrase or math teaching phrase. This is like this is everything, right? So it’s like, do I do I waiver? Or do I adjust my beliefs if I have new evidence that support otherwise?
Jon Orr: That’s why you want to have them loosely held because if you strongly hold them, you’re basically saying like, I’m never going to switch my thinking here. And even though it’s staring me in face.
Yvette Lehman: And I guess the, you know, just to conclude here today, like why does this matter? You know, like why is this work important and why should we be striving to build up wherever we’re lacking? Like, is it your conceptual that needs to be strengthened or is it your procedural that needs to be strengthened? Like, why do we need to engage in this work? And I’m gonna give you a personal example of why this matters to me.
I think we can all agree and I’m sure all of the listeners today agree. We want students to have a productive, like I don’t want students to say math is the class they hate. Like I just don’t want that for them. Like I want them to see that math is interesting and math is, know, positions you to be a problem solver and that they’re capable. And I’m gonna give you a perfect example. So my son who’s in grade five.
is working on patterns right now. He’s working on linear patterns and he had, you know, a very standard growing linear pattern. The pattern was three, six, nine, 12, 15, 18. He was asked to write the pattern rule two ways. And the first one said, write the pattern rule using addition. And so he said, okay, start at three, add three each time. The second question said, write the pattern rule using multiplication. And he got this one wrong.
Jon Orr: Okay. Okay.
Yvette Lehman: And he said to me, he said, know, I don’t know, I was overthinking it. It’s just multiply by three. It’s like three X. Like I should have known that. But this is how he interpreted it. He looked at the relationship between three to six to nine to 12 multiplicatively. So he was like multiply by two, then multiply by one and a half, then multiply by one and a third, then multiply by one and a fourth. Okay, because he understood the multiplicative comparison between the numbers in the pattern.
Jon Orr: Nice.
Yvette Lehman: Can you imagine though, like if I had a very procedural teacher who was coming from your end of the spectrum, right? Wrong. But in reality, like amazing thinking for a 10 year old that he’s like, he was like, I need to look at this pattern through a multiplicative lens. He wasn’t, you know, of course, like he wasn’t thinking the relationship between X and Y. He was looking at the values of Y.
Jon Orr: Yeah, that’s wrong.
Yvette Lehman: and he described how they were being multiplied. And so there’s two experiences he can have, and this is just one kid. He can be told he’s wrong and get a zero and that’s it. Or his thinking can be valued and that will affirm his identity as a mathematician.
But in order to be positioned to affirm student thinking, to help them be thinkers and critical thinkers and see themselves as that like math is about making sense and seeing relationships and reasoning, we have to be positioned to see it. And if we don’t see it, math class becomes very black and white for kids, right and wrong.
Jon Orr: Very much so. Yeah, it’s the belief we have about what math is and what math class is versus I guess that’s it. It’s like, what do you believe to be true about the experience you’re providing? Like, what is it that you’re trying to do in that class? Because my first 10 years, I was probably that teacher. I would have marked that wrong because I held strongly, you know, I had strong beliefs and I strongly held them about what math was and math was about.
doing, you I taught you this and now you need to show it to me over here. And hey, wouldn’t, Leto, why wouldn’t you know that I meant, you know, three X, come on. Like I went through example one, two and three already, you know, and it’s like, because you have these like beliefs of like, this is what it’s supposed to look like. This is what I’m looking for. This is the answer. Otherwise you’re wrong. That’s a strongly held belief, strongly held.
Yvette Lehman: Yeah, so this is why the work, right? This is why we have to take the time to strengthen both our conceptual and our procedural. And I think that, and our mindset for sure.
Jon Orr: And her mindset like, like, think about like, that right there. It’s like, if I, in a way, here’s, here’s another, you know, one of your big, one of our big takeaways here is like, everyone should find someone with the opposite viewpoint, and try to learn from them. So you’re, you’re actually going, I have strong beliefs, but I’m loosely holding them. And I’m going to learn from this person. And they’re going to have something to teach me. And
If it’s a mindset shift about what you’re doing in your math class, then find that person who has the opposite mind mindset and have that conversation. What are they, what are they doing in their class and what can you pull for your experience to help with your students? And then maybe, maybe they also have some of that open mindedness at that point to have that say, get that next step from you, even though that, that experience for your example before wasn’t the case, that teacher wasn’t looking to learn anything from you.
you learn from them and you needed to take what they had and apply it to your learning, we can do that with mindsets as well, other than just conceptual understanding to procedural fluency.
Yvette Lehman: think if we can do this work, if we can find these people, if we can learn from each other, then we’re going to avoid the math wars or these big debates because none of it is black and white and none of it is all or nothing. Of course we need students to know their facts and we need them to demonstrate fluency. Of course we want them to be able to be efficient and generalize and use algebraic representations. Of course we do. That’s the goal.
But that doesn’t mean that we have to do that by relying solely on memorization. Because we just know that, like me, it’s not going to work for everybody. We’re not going to reach as many students if we focus on this one approach that worked for, you know, let’s say you. We just know it’s going to leave out so many students. So can we get to the same result?
but in a way that’s going to create a more equitable math experience for all learners that’s rooted in understanding that’s going to support retention.
Jon Orr: Love it. Find your people, folks. Find those people that are not your people. Both of those, the messages here. And, you know, it’s hard work to do that. You know, you have to put yourself out there, but also you have to be ready for the, say, that person who is, isn’t going to say, be part of that conversation when you need them to be or want them to be. But, you know, these are some of the big takeaways we’re hoping you have going forth and doing the great work that you’re doing in your classrooms.
Let us know, what was your big takeaway from this conversation that Yvette and I just had here? Let us know. You can reach out to us on all social media platforms, at Make Math Moments. You could hit reply on our email list. know, we’re putting, you know, we’re probably sending you a few emails throughout a week or every couple of weeks. Hit reply, let us know what is your big takeaway from this particular episode. And we would love to hear from you about that.
Thanks For Listening
- Book a Math Mentoring Moment
- Apply to be a Featured Interview Guest
- Leave a note in the comment section below.
- Share this show on Twitter, or Facebook.
- Leave an honest review on iTunes. Your ratings and reviews really help and we read each one.
- Subscribe on iTunes, Google Play, and Spotify.
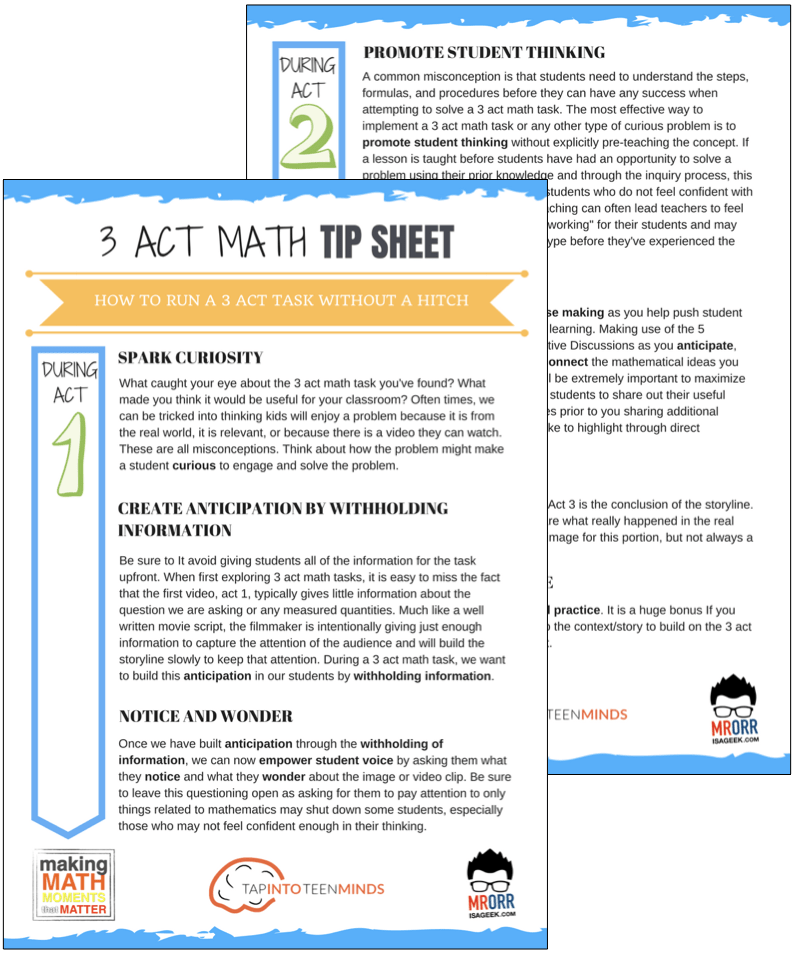
DOWNLOAD THE 3 ACT MATH TASK TIP SHEET SO THEY RUN WITHOUT A HITCH!
Download the 2-page printable 3 Act Math Tip Sheet to ensure that you have the best start to your journey using 3 Act math Tasks to spark curiosity and fuel sense making in your math classroom!
LESSONS TO MAKE MATH MOMENTS
Each lesson consists of:
Each Make Math Moments Problem Based Lesson consists of a Teacher Guide to lead you step-by-step through the planning process to ensure your lesson runs without a hitch!
Each Teacher Guide consists of:
- Intentionality of the lesson;
- A step-by-step walk through of each phase of the lesson;
- Visuals, animations, and videos unpacking big ideas, strategies, and models we intend to emerge during the lesson;
- Sample student approaches to assist in anticipating what your students might do;
- Resources and downloads including Keynote, Powerpoint, Media Files, and Teacher Guide printable PDF; and,
- Much more!
Each Make Math Moments Problem Based Lesson begins with a story, visual, video, or other method to Spark Curiosity through context.
Students will often Notice and Wonder before making an estimate to draw them in and invest in the problem.
After student voice has been heard and acknowledged, we will set students off on a Productive Struggle via a prompt related to the Spark context.
These prompts are given each lesson with the following conditions:
- No calculators are to be used; and,
- Students are to focus on how they can convince their math community that their solution is valid.
Students are left to engage in a productive struggle as the facilitator circulates to observe and engage in conversation as a means of assessing formatively.
The facilitator is instructed through the Teacher Guide on what specific strategies and models could be used to make connections and consolidate the learning from the lesson.
Often times, animations and walk through videos are provided in the Teacher Guide to assist with planning and delivering the consolidation.
A review image, video, or animation is provided as a conclusion to the task from the lesson.
While this might feel like a natural ending to the context students have been exploring, it is just the beginning as we look to leverage this context via extensions and additional lessons to dig deeper.
At the end of each lesson, consolidation prompts and/or extensions are crafted for students to purposefully practice and demonstrate their current understanding.
Facilitators are encouraged to collect these consolidation prompts as a means to engage in the assessment process and inform next moves for instruction.
In multi-day units of study, Math Talks are crafted to help build on the thinking from the previous day and build towards the next step in the developmental progression of the concept(s) we are exploring.
Each Math Talk is constructed as a string of related problems that build with intentionality to emerge specific big ideas, strategies, and mathematical models.
Make Math Moments Problem Based Lessons and Day 1 Teacher Guides are openly available for you to leverage and use with your students without becoming a Make Math Moments Academy Member.
Use our OPEN ACCESS multi-day problem based units!
Make Math Moments Problem Based Lessons and Day 1 Teacher Guides are openly available for you to leverage and use with your students without becoming a Make Math Moments Academy Member.
Partitive Division Resulting in a Fraction
Equivalence and Algebraic Substitution
Represent Categorical Data & Explore Mean
Downloadable resources including blackline masters, handouts, printable Tips Sheets, slide shows, and media files do require a Make Math Moments Academy Membership.
ONLINE WORKSHOP REGISTRATION

Pedagogically aligned for teachers of K through Grade 12 with content specific examples from Grades 3 through Grade 10.
In our self-paced, 12-week Online Workshop, you'll learn how to craft new and transform your current lessons to Spark Curiosity, Fuel Sense Making, and Ignite Your Teacher Moves to promote resilient problem solvers.










0 Comments