Kyle Pearce: Hey, hey, hey Math Moment Makers from around the globe. Do we have another great episode ready for you to gobble up today?

Jon Orr: We are bringing you another Make Math Moments masterclass. Do you know what concept is holding your students back the most? Just say it out loud right now. Go ahead. Don’t whisper it.

Kyle Pearce: Say it.

Jon Orr: What is holding your students back? Don’t worry about who gives you looks. If you’re in the teacher prep room or on the train or even if you’re on your run and someone hears, just give it a try. Go ahead. What is holding your students back the most?

Kyle Pearce: Jon, do you know what I think is holding my students back the most?

Jon Orr: I think I know what you think.

Kyle Pearce: Proportional reasoning.

Jon Orr: Bingo.

Kyle Pearce: We have found that reasoning proportionally is the concept that prevents so many students from developing a deeper level of thinking towards number sense, algebra, measurement and functions. When we say that math facts like multiplication tables and students’ lack of ability to recite them is the problem, then sometimes that’s just the canary in the coal mine.

Jon Orr: In this episode, we’ll explore why our students are struggling with this concept, how we can help students from various grades and how you can develop a deeper understanding of proportional reasoning so you can ensure your students get that deep learning you’re looking for.

Kyle Pearce: So, if you’re ready, my friends, you should hang on tight because…

Jon Orr: Here.

Kyle Pearce: We.

Jon Orr: Go.

Kyle Pearce: Welcome to the Making Math Moments That Matter podcast. I’m Kyle Pearce from tapintoteenminds.com.

Jon Orr: And I’m Jon Orr from mrorr-isageek.com. We are two math teachers who together…

Kyle Pearce: With you, the community of Math Moment Makers worldwide who want to build and deliver math lessons that spark engagement…

Jon Orr: Fuel learning.

Kyle Pearce: And ignite teacher action. My friends, welcome to episode number 65: the concept holding your students back. We’ve got another audio master class for you.

Jon Orr: We are pumped to share this episode with you and we’re so happy to hear how pumped you are when we read your ratings and reviews on Apple podcasts.

Kyle Pearce: Just like Apple podcast listener, This Podcast Matters. We’re not kidding, that’s the actual name of the person-

Jon Orr: That’s the name.

Kyle Pearce: … who left this review. This podcast matters left us a five star rating and a review that said…

Jon Orr: Changed my teaching. This podcast has been so instrumental in changing my discourse with fellow teachers about math and math resources. I have introduced so many people to the resources and ideas I’ve heard here because it has made me excited again about working with students and letting them do the problem-solving and explaining. Thank you for all you are doing to improve math instruction around the world and support and encourage teachers.

Kyle Pearce: We are now at over 190 ratings and over 80 reviews on Apple Podcasts alone and we can’t thank you enough. Keep them coming because the more ratings and review the show gets, the more educators who will be able to find it online on their favorite podcasting platform.

Jon Orr: All right. Before we dive into this audio masterclass, we want to get a goodie into your hands that’s going to help you solidify the learning you’ve done here with us in this episode.

Kyle Pearce: We’ve built a roadmap to proportional relationships starting at comparison using spatial reasoning all the way through counting, additive thinking, multiplicative thinking and into ratios and finally proportional relationships. The Make Math Moments course titled the concept holding your students back uses this roadmap to take educators on a journey through nine modules of proportional reasoning bliss to highlight some of the areas that students and even we, the teachers have struggled with in the past or have just been completely unaware of until now.

Jon Orr: To grab this great one page roadmap to proportional relationships cheat sheet head to makemathmoments.com/proportion. That’s makemathmoments.com/proportion.

Kyle Pearce: All right, let’s dive into the learning.

Jon Orr: All right. All right. Let’s get into this. Kyle, how are you doing this day? How are things going over on your end of the County?

Kyle Pearce: Oh, I am doing just fine, my friend. How about you? I know that recently there’s been a few little labor disputes here in Ontario and you took the brunt of it and had to go walk a line for a little bit today, I think.

Jon Orr: That’s right. That was my day today. Sometimes we do big wins here when Kyle and I do our audio masterclasses. And my big win today, I wasn’t in the… actually, it’s not really a big win. I was not in the classroom today. And yeah we were walking the picket lines today, kind of a standing up for education here in Ontario. So, that wasn’t too awesome that we had to do that, but we have to do that. Kyle, what was your big win over on your side today?

Kyle Pearce: Yeah, for me, I got the chance to hang out in a classroom because right now we are dealing with some job action issues here in Ontario. The negative is that a lot of PD recently had to be rescheduled because of all the different job actions going on with unions. But on the bright side, the one thing that I do get to do more now is I actually get to go and hang out with even more students and teachers. So I’ve been in a lot of classrooms and today I got to do a bunch of really cool algebra stuff using a context for learning unit.

Kyle Pearce: It was the frog jumping unit from Kathy Fasano and she was on one of our early episodes. But what a cool unit. We were using the double number line to help students essentially bump into the idea of algebraic substitution and then trying to help them see it both symbolically as well as visually and making that connection so that they can move towards solving systems of linear equations.

Jon Orr: I like it. I’d be interested to hear more about that in particular. But today let’s dive into this audio masterclass all about the concept holding our students back. We want to talk about today what is it and what is that concept holding our students back exactly and why is this concept the one that is holding our students back? Kyle, I know that you’ve gone on a journey on this recently. And actually not recently, but over the last couple of years. And I’ve been learning a lot from you that I’ve been applying in my class, but let’s talk about proportions. That’s our focus here on this episode. Let’s talk about how we can help our kids on that. And maybe before we get into how we can help our kids on that and why it’s the one holding our kids back, maybe we talk about what we did with proportions.

Kyle Pearce: Right. Right. Yeah, absolutely. I know Jon, you and I having been down many of the same roads in terms of the courses we’ve taught, one of those courses we talk about a lot on this podcast it’s like the one that has that soft spot in our heart is all of those grade nine courses that we taught and there’s a heavy focus on proportions and leading into linear relationships. And for many years I felt like I had a grasp on it. Like I could solve proportions, I could identify proportions and scenarios that had proportional relationships.

Kyle Pearce: And I would just teach them very procedurally. And Jon, I know you were very similar in terms of how you were taught and how you approached it, but I was always trying to look for the way to make learning math of all types, but also proportional relationships as easy as possible. So, I was constantly handing students tricks and I know one that many people would be familiar with is this idea of cross multiplying.

Kyle Pearce: And Jon, did you have any like go-to strategies that you would handover to students that now I know that you and I have both really, really pumped the brakes on that and said, “Whoa, Whoa, Whoa, there’s a better way.” But what were some of those ways just for those who are listening? Maybe there are some people out there they’re like, “Hey, I used to do that too.” Or maybe, “I’m currently doing that,” and we’re trying to shift beyond that.

Jon Orr: Yeah. You know, you bring up cross multiplying and I remember my grade eight, grade nine years and trying to cross multiplying and confusing that idea with solving equations and always thinking I have to multiply that by that. And I didn’t understand why that worked. It always stuck with me and as I got into teaching, I was one of the first things I really did not want to teach my students. I was never a cross multiply kinda teacher. Like I never showed my kids cross multiplying.

Jon Orr: And instead I tried to show them just the basics of solving equations. But Kyle, it was still very procedural at that time even though I knew that I wasn’t a cross multiplying, I just didn’t want to go down that route because I actually probably didn’t understand exactly why it worked anyway, so I developed other procedures. I remember not even too long ago telling kids how to solve proportions in the grade nine applied class that we would just say, “Okay, you set up this proportion.”

Jon Orr: I’d always make sure that you’ve got these two fractions equal to each other. And I even used the words, like I made the step-by-step procedures. Like step one was divide the side you know. There was always one variable on one side, right? You don’t know that side and you don’t know that value. So you divide the two that you do know. And then it was okay, now multiply by the opposite denominator. That was it. That was like my two, three steps.

Jon Orr: However, I remember teaching that whole semester those steps, kids could solve proportions like the wind. And you know what showed up on that standardized test Kyle? The unknown was in the denominator. So it’s like-

Kyle Pearce: Crush and burn.

Jon Orr: … kids are dividing the side they know and then multiplying by the number and they’re getting it all wrong. I’m like, “Oh geez.” I’m just showing them how to solve this proportion, but we never really looked at a ton of problems where the thing was the denominator. You know what I did after that Kyle? I said, “Okay, step one needs to modify. Make sure the numerator is the unknown. Flip it around.” It was just kind of just modifying for all these different scenarios.

Kyle Pearce: Like a bandaid solution. Right?

Jon Orr: Exactly.

Kyle Pearce: Bandaid solution that you had to get you out of one more jam. Yeah, I totally can relate. It’s been for me, very similar journey. And I think when we zoom out now knowing what we know, when I was in that moment, it never occurred to me that there was an issue with that. I think it’s because I had such a narrow thought of what my hope was for students in terms of learning in the math class. It was like I was all about answer getting and if they could get the answer, then I thought that’s what the game was all about.

Jon Orr: We’re good move on.

Kyle Pearce: You know, I just didn’t know any different. And for those who are listening, if you feel like maybe you’re stuck in that zone, don’t beat yourself up over it. I mean it’s, once you know better you do better. And for us, how did you ever break free of that Jon? What was some of the things that helped you emerge from there?

Jon Orr: I think it was actually some of the learning that we did together and we built off, I built off you and you showed me some nice tools that we can use in our classrooms to help model what a proportion might look like. And since knowing that, I’ve shied away from those standard procedures of just showing kids how to do this. And I think Alex Lawson calls these things models with legs.

Jon Orr: It was great to be like, “Let’s use tools that can do more than just this one thing.” And I think that has helped me a lot and I know that you have helped me along that journey, but we’ll get into all of that and how that can help us with proportional reasons and what specifically we’re talking about. But Kyle, let’s go back a little bit because I know that you’ve been helping me, but I know that you got help with other people. So, let’s go into a little bit of the background on your learning, but also this will set the stage for why this topic is so important for our students and not just so they can solve proportions, but so they can do so many more math topics.

Kyle Pearce: When I think back, and you had referenced how we had done a lot of work together on planning our grade nine course and we were talking about models. And I remember at that time because we were so new at it, we had bumped into some different models. And even though I still think we were doing way better than we were prior to introducing the models. Even then we were using those models more procedurally. Right? Like teaching kids how to use that model versus emerging it somehow. And that’s been the journey we’ve been on really. I think it’s really hard to realize what you don’t know.

Kyle Pearce: I was having a discussion online, I think it was on Facebook and we were talking about ratios and the discussion of like is a ratio a fraction or not? And interestingly enough, even research that’s out there, there’s some confusing language out there as to whether a ratio is a fraction or is a ratio and a rate the same? So we were having all these discussions and back then, my understanding is now evolved since then, but I had a pretty convincing argument for why a ratio could be a fraction.

Kyle Pearce: I now don’t believe a ratio itself can be a fraction. I actually believe that you would have to reveal a rate to essentially convert it into a fraction, but we’ll talk a little bit more about that later. But it was through this discussion and we’re going back and forth, and James Tanton was in on that discussion and randomly a few days later, he had sent me a message and said, “Hey, do you want to come to Arizona? We’re doing a proportional relationships symposium.” I’m like, “Oh wow.”

Kyle Pearce: I know James, I didn’t know him really well at the time, but he said, “I’d like to have your voice there and really to bring some of the teacher voice to the forefront and really just get a bunch of people in a room and do a think tank.” So, we had a list of, I want to say it was 25 different people were there. Some of the common core writers, like Phil Daro was there and Will, or Bill McCallum is there. He’s now with the Illustrative Math and all kinds of great people, including researchers. James was there, Scott Baldrige from Eureka Math was there. And just having this discussion with so many knowledgeable people, knowledgeable others in the math space was just mind blowing.

Kyle Pearce: And I remember telling you after the first maybe hour I was in the room and there was essentially a debate about what is a quantity? And everyone had different definitions of what that meant to them and what’s required and so on and so forth. And I was just mind blown at how many nuances there were to the math that I thought I understood and then I realized I really didn’t.

Jon Orr: Right. Like no agreement.

Kyle Pearce: Right. Right.

Jon Orr: Is that what you’re saying? Like everyone had their own thoughts on like this. It’s something that we take for granted thinking about what’s a quantity and it’s all of a sudden everyone has got a different opinion and that seems crazy.

Kyle Pearce: And it seems so simple too. Like someone says it’s simply, but then somebody else says, “Well no, not really.” And then they add a little and then you kind of see everybody’s, in their eyes, you see them thinking through these ideas and going like, “Yeah, I guess that makes sense.”

Kyle Pearce: And I remember in that conversation as well, something I learned and it was, we were there for two days. We actually did this twice, so we had two weekend gatherings. And it was through this group that I was introduced to the two types of division, which anyone who’s followed any of the things I do on mathisvisual.com or are part of the Academy or the online workshop, they see this idea of these two types of division constantly coming up. And it was through discussions at this think tank that I was like, “Oh my gosh, I can’t believe that I was completely unaware of this. I have a math degree and it just never dawned on me that when I’m dividing I’m doing one of these two types.

Kyle Pearce: And it’s probably highly likely that half of the time it was one and the other half of the time it was the other and I just had no idea. So, that was just mind blowing to me.

Jon Orr: Wait Kyle. Kyle, I am a math teacher who also has a math degree. You got to fill me in. There’s two types of division?

Kyle Pearce: Yeah. And it’s so crazy and I mean, I guess it’ll give us a little bit of foreshadowing into what we’re going to talk about today with this roadmap because the two types of division are actually really important for getting us closer to this idea of proportional relationships is that there is something going on with these two types of division that if I don’t have that experience, it can really hinder my understanding, my conceptual understanding or my ability to conceptually understand some of the more complex things like developing a proportional relationship or building an equation, a proportional equation or an algebraic equation for a proportional relationship.

Kyle Pearce: But if you think back, typically when we introduce division to students, we typically introduce it through this idea of fair sharing, Jon. Like I’m sure you’ve been in that scenario, or you remember with your own kids even. You’ve got cookies and-

Jon Orr: There’s 24 pencils and we’ve got to give them to six people, right?

Kyle Pearce: Yeah.

Jon Orr: So it’s like, let’s fair share.

Kyle Pearce: Yeah. So you’re going to fair share that, right? I go to this idea of like cookies and today I was at work and we’re having a discussion about types of division and a few things with a colleague of mine, Yvette Lehman. And she likes to use the scenario of cookies and plates. It could be people but like cookies and plates is her way to go. So if I was to frame that and say, “Okay. Well, I’ve got 12 cookies and I’ve got three plates and then what do you do?” You take one cookie, you put it on one and then one for this one, one for that. And you keep doing this over and over again until you run out. And what do you know? You end up with four cookies on each of the three plates.

Kyle Pearce: That is one type of division. That fair share division is often called partitive division because we’ve taken it, we say there’s three plates. It’s like we’re taking the 12 cookies and we’re going to partition it into three parts, into three different plates of cookies. But if we think about it, I could also take the same context and give you a different amount and say, Jon, instead this time we have 12 cookies and I want to make sure that everybody gets three cookies each. What are you going to do now when I tell you that?

Jon Orr: I have to ensure that everyone gets three cookies each. So I have to figure out how many plates.

Kyle Pearce: Yes. So you don’t know how many [crosstalk 00:19:02] there are.

Jon Orr: I have to figure out how many plates there are.

Kyle Pearce: Exactly.

Jon Orr: Okay, so then-

Kyle Pearce: So what you’ve just uncovered is this other type of division. So, go ahead and think about how you would do that if you didn’t already have the known fact of what 12 divided by three is.

Jon Orr: Yeah, I would think that almost like the three is now a plate. So I think I put three over here and three over here and I keep doing that until I showed up. Oh, I got four groups out of that.

Kyle Pearce: Holy smokes. So it’s like same idea, but because I’ve given you the other piece of information, this idea of like I told you, the rate is what I gave you. I said I want everyone to get three cookies, I think.

Jon Orr: Three.

Kyle Pearce: I’m losing track of what I gave you, but I think I said three per person. So, when I say that three per person, what I’m giving you is I’m actually giving you the rate. Before I give you the parts, now I’m giving you the quota or the quantity per group. And now you have to tell me how many groups I’ll get. And actually when you do that division, whether you realize it or not, sometimes people feel like it’s still fair sharing, but you’re not actually doing that. You’re actually repeatedly subtracting three from the group.

Jon Orr: Right. That’s what I was doing.

Kyle Pearce: So you think I had 12 and I take three away. I put them over there, I take three more away, I put those over there. So it feels like fair sharing because you’re still putting them somewhere, but the difference is, is that before I had to like one to one fair share and now it’s like no, no, I’m going to take away units of three until I run out.

Jon Orr: Interesting.

Kyle Pearce: Yeah. And some kids will repeatedly add three until they get there. So they use more of like additive approach versus subtracting. Yeah. But those are the two types of division. And again, right under my nose and right under your nose, but it’s like until you actually draw your attention to it, we as educators oftentimes we just do this stuff and we don’t even think about it. And interestingly enough, when we start with young children, we tend to do fair sharing we’re like, “Here, split up the cookies or split up the pencils like you said.”

Kyle Pearce: And then we get to long division, teachers will rush to the long division algorithm and then we’ll switch the language on kids without even telling them and without us even realizing it we’ll use words like goes into. So, the second scenario was a goes into. How many times does three cookies go into 12 cookies?

Jon Orr: Right. Because then you’re going to repeated subtraction.

Kyle Pearce: Repeated subtraction. So you flip the script on the kids without them realizing it and without you even realizing it. And it’s all because when we were younger, we just thought division was division and that’s it.

Jon Orr: This actually is so interesting because it goes back to the discussion you guys are having at that Arizona mathematics partnership, that there’s all these intricacies and these things that this guy knows this or this girl knows this and this person knows this, that they’re bringing to that table that you guys all sat at and add this into it. It’s no wonder that there’s so much confusion happening.

Kyle Pearce: I guess the part I always want to make sure we’re really clear is, anyone who’s listening, I don’t want anyone to feel anxious or stressed about this. This isn’t like, “Oh my gosh, I don’t know anything.” It’s not about that. It’s about us just having that awareness because I had no awareness of what I didn’t know. Right?

Jon Orr: Yeah.

Kyle Pearce: I just was ignorant to it. And now that I know-

Jon Orr: Kyle, I just learned this tonight.

Kyle Pearce: Yeah, yeah, exactly. It was like how many years old? I was today years old when I learned that or something like that.

Jon Orr: Yes. That’s what I was going to tweet out right now. I was today years old when I learned that there was two types of divisions.

Kyle Pearce: Right. And this is happening in math all the time. It’s happening all over the place. And when I think back to one of the people that was there was a really, really passionate math educator, Dick Stanley, he’s from Berkeley in California and he has been on this proportional reasoning, proportional relationships train of trying to make education and middle school better and really trying to un-muddy the waters, clear the waters in those middle years to try to help kids get over this big hump.

Kyle Pearce: And he shared with me a story when he was presenting back in 2014 and he was at, I can’t remember the conference, I think it was in Arizona as well. And he asked a group of middle school educators and it was, I think 50, a hundred people in the room. He said, “What does it mean in general to say that one quantity is proportional to another quantity?”

Kyle Pearce: And then he asked them to be as precise as they can and gave some turn and talk time to let them go. And I’ve now done that. Any time I’m presenting in regards to proportional reasoning or proportional relationships, I ask this question so we can get this discussion going. And he said, it was actually disturbing when he got the confusing jumble of responses is what he said. He said the confusing jumble of responses here is disturbing. At the very least it points to a lack of common understanding within the school math community of this very basic and important subject.

Kyle Pearce: And he said it would certainly be wrong to blame teachers, but rather he believes the culprit is a general lack of mathematically sound grade level appropriate presentations of proportionality that have been available to teachers. And I think he couldn’t have said that any better. By, again, this is not a point the finger and blame teachers, it’s the fact that none of us were exposed to any clarity in this area, so how is it going to be possible for us to all be clear when we try to come together and discuss something like. I mean, math is complex but proportional relationships. It seems so easy when you look at it from a distance, but then when you actually go and try to unpack it, you realize there are so many things going on that can go unnoticed.

Jon Orr: Yeah. This confusion is actually like what Dick Stanley there said like disturbing. But with all these educators having this confusion, I’m wondering what is happening to students? This has got to be a reason that our students are falling behind on proportional reasoning. Don’t you think, Kyle?

Kyle Pearce: Absolutely. And if you look at even standardized test results here in Ontario, Ontario’s been taking a little bit of a raw deal when it comes to like-

Jon Orr: Especially in grade six.

Kyle Pearce: … [crosstalk 00:25:17]. Yes. In grade six there’s been a lot of media coverage really bashing the idea of how math education isn’t working in Ontario when in reality, our standardized test is actually assessing quite deep thinking of students. And yes, there have been some struggles. But in particular, what’s been uncovered through the data over many years now is that one of these big areas that students tend to struggle in is this idea of proportional reasoning and proportional relationships.

Kyle Pearce: And in particular, on the 2018 junior assessment, which all grade six students here in Ontario take the summative or this, I should call it a standardized assessment at the end of grade six. One question in particular really stood out to us at our district because it was the question that students struggled on the most. And when we compared it to the province, the province also struggled with it the most. We were like, in some ways it was a relief. It wasn’t just us, but also all the students in Ontario. And some people could point the finger at, maybe it’s just a bad question, right?

Jon Orr: Yeah.

Kyle Pearce: But I think it’s more than that. And Jon, I know you know the problem.

Jon Orr: Yes sharing.

Kyle Pearce: Do you mind sharing what is the problem we’re referencing?

Jon Orr: We actually just shared this problem on our webinar that just went out, the four different webinars we did in January. We asked teachers in that webinar to read this problem and then try to do a makeover on it to make it more curious and engaging. But this is the jugs of milk problem from the 2018 released materials from EQAO here in Ontario. I’ll just read this out loud. We’re going to put an image of this up on the website. So, if you’re heading to makemathmoments.com/episode 65 that’s where you’ll find this image.

Jon Orr: So, if you’re on a computer right now, you can head there and you’ll see this problem that we are going to read through here. So let’s read this problem here. It says Tyson empties six jugs of milk into a container. Each jug contains four liters of milk. He uses the container of milk to fill cartons. Each carton requires 250 milliliters of milk. How many cartons will he be able to fill? And then there’s four options here. 16 cartons, 24 cartons, 63 cartons or 96 cartons.

Jon Orr: Yeah, Kyle, this looks a little complex. You’ve got grade sixes who are now have to think, I’ve got these milk containers and there’s so many of this and this and there’s so many of this and this and how many of these we got to fill up? There’s a lot going on here.

Kyle Pearce: Yeah, you’re absolutely right. And I think, again, I really don’t think it just comes down to poor wording of the question or an unfair question. I don’t think it’s an unfair question at all if students have developed proportional reasoning skills. And I think the key word is reasoning, right? If they can reason through this problem, I don’t see them having a huge issue. There is one key piece of information that students would have to know and they would have to know that there are 1000 milliliters of liquid in one liter. That is really the only piece of information that they need to know.

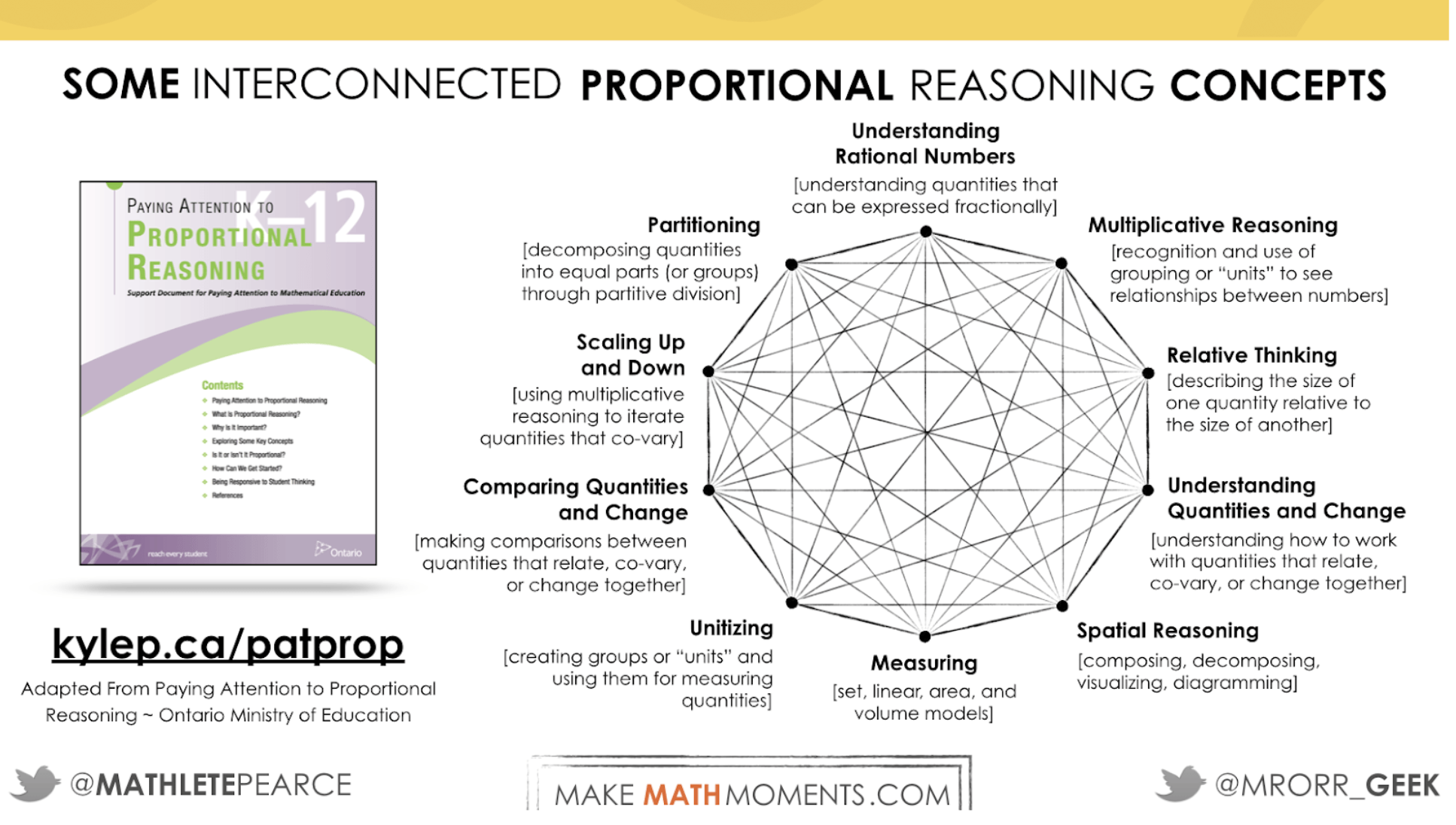
Kyle Pearce: And I mean here at the metric system that’s not like a huge stretch for them to know that. So, I really don’t feel confident that that’s the actual issue. But when we rolled back to some of the resources that are out there, and in particular for me, one that really caught my attention through a lot of the PD that I had been a part of over the past number of years. Here in Ontario, we have these documents that were titled paying attention to and there were actually five in the series. The first was mathematics and then they had spatial reasoning, and proportional reasoning and algebraic reasoning. And I think the other was fractions.

Kyle Pearce: And when you open up the proportional reasoning guide, they had this thing they called the interconnected proportional reasoning concept web. And it’s like this web showing all of these big ideas. And there’s about 10 ideas here that talk about all of the key understandings that you need to build proportional reasoning skills in order to be able to think proportionally and multiplicatively. And when we looked at all these in this problem, we actually saw that essentially every single one of them could be connected to that particular jugs of milk problem, which to me was completely mind-blowing that that many concepts could in some way, shape or form be connected to that one particular problem.

Jon Orr: And you know what’s interesting about this interconnection I find is that the reverse thing has to be true too. It’s that we have to be good at all these to be good at proportional reasoning. But also to be good at proportion reasoning, we have to be good at these things too. So, they’re connected. Here are a couple of things, you have to understand rational numbers, we have to understand multiplicative reasoning, relative reasoning, spatial reasoning, measuring.

Jon Orr: This is something that sometimes you just take for granted that there’s so much measuring. In this particular problem we got the jugs of milk, there’s measuring involved in here and measurement. However, you sometimes take it for granted that in order to, say, solve problems with measurement, you’ve got to be good at proportional reasoning. So, there’s unitizing on this web and comparing quantities and scaling up and scaling down. It’s very interesting all of those connections and no wonder if you have to be good at all of these things to be good at proportional reasoning. It’s tough to say the kids are not doing great proportional reasoning. There’s so many things involved in it.

Kyle Pearce: Absolutely. I think if I was even maybe two, three years ago, I look at that problem, I would just say, “Oh, it’s just a conversion probably.”

Jon Orr: Right, exactly.

Kyle Pearce: It’s just conversions, it’s no big deal. Get a staircase, get a whatever. It’s a word problem. That’s the issue. Yeah. And to me now it’s so obvious now that I’ve been diving into this so deeply. But again, it would have never been obvious had I not done or had that opportunity to go and really be exposed to it. So, that’s really why we’re sharing this episode with folks now. And for us in our district when we went digging through and we were running a workshop and we were really trying to think about how can we help educators from K through 10? K through grade 10 in our district get an understanding?

Kyle Pearce: Because we have a firm belief that if I’m teaching in the early years, I don’t necessarily have to know all the way to grade 10, let’s say, but I do need to know a fair ways off into the distance of like where kids are going. And we say that all the time-

Jon Orr: Exactly.

Kyle Pearce: … on this podcast as well as in our online workshop. But then the opposite is true as well. If I’m teaching grade nine, like Jon, you and I, we taught grade nine for over 10 years before we were starting to really dive into this and the reality is it’s like I didn’t know what kids needed in order to build the reasoning skills, the actual ability to participate in the mathematics that I was hoping for them to learn in my classroom.

Kyle Pearce: And if I didn’t know that, then it made it really difficult for me to even notice what they were missing, let alone try to actually do something about it and help them out. For us, we looked in grade four and we saw that in the grade four curriculum here in Ontario, the word rate comes up for the first time. One of the expectations is demonstrate an understanding of simple, multiplicative relationships involving unit rates.

Kyle Pearce: And I have a philosophy on unit rates itself. We talk about rates and unit rates, and now I’ve come to realize that really a rate’s a rate’s a rate. It’s not really a unit rate. But again, when I look at that and I look at grade four and say, “Wow, if there’s so much confusion out there about what a proportional relationship is and what a rate is, let’s say, or a ratio is, that’s really difficult.”

Kyle Pearce: So we went and we said, “Let’s do this PD.” So we said, “Let’s pull a couple sample problems right from the textbook so that we can help teachers work with what they have and do some learning.” So we pull out the grade four textbook, open it up, I’m scrolling through the book, I’m flipping pages, and I remember Yvette at the time, and Andrea at the time were flipping through the book and we could not find anything. I said, “Oh, I’ll just go to the back. I’ll just look at the index, the word ratio, proportion, multiplicative comparison.” These ideas were not in the grade four textbook. That’s a tragedy obviously.

Kyle Pearce: We’re like, all right. Well, let’s just go to grade five and we’ll be done. We go to check there, same issue, not in the grade four or grade five textbooks. So I wonder how as an educator you’re going to have a resource to be able to help their students see these stuff.

Jon Orr: So, it’s in the curriculum documents and if those of you listening not from Ontario curriculum documents for us are the standards. So if it’s something that we’re supposed to teach, it says involving unit rates through investigation. And in grade five it says whole number rates in multiplicative relationships through whole number rates. And you’re saying that the textbooks that most teachers rely on for their sequencing and how they’re laying out their courses is not even in those, say, Ontario’s certified textbooks.

Kyle Pearce: Right. Yeah, exactly. And this is one of these challenges that, especially here in Canada where a lot of publishers, I think the rule is, don’t quote me on this, but I think the rule is for it to be added to what we call the Trillium List. I think 80% of the curriculum has to be covered in the textbooks so that it can be added to this, we’ll call it approved list. But that also means they could have a bunch of other stuff added, right? So it’s like 80% coverage, but there could also be another hundred percent of something else. Right?

Kyle Pearce: So not only are you dealing with maybe not having everything from your curriculum there, but then also you might have a bunch of other stuff that you have to filter through and say, “Is this actually my curriculum or is it actually in some other curriculum?”

Kyle Pearce: So, there are those challenges, but then it makes me wonder why in grade six we’re struggling so much here in Ontario. I wonder if many districts are encountering the same issues where maybe some of their core resources are missing some of these fundamental concepts that kids aren’t getting inappropriate amount of experience with. Again, not the teacher’s fault, this isn’t a fault thing. It’s just an awareness thing for us to be like, “Wow, if that’s not happening, then kids aren’t developing those concepts if I’m not intentionally bringing them to the forefront.”

Jon Orr: It’s a definite shame that the main resource that most teachers use it is not in there and you’re absolutely right. By the time they get to grade six, by the curriculum standards, it’s saying they should have had two years already of working with rates. If anything, Kyle, I think this is a huge indicator to do something we’ve always preached is, is to make sure that you are referring to the curriculum guideline, the curriculum standard and not the textbook so that you can make sure that you’re covering what you’re supposed to be covering.

Jon Orr: But like you said, not normally the fault of the teacher only because most schools will say follow this textbook, this is what we’ve provided for you for that class. But yeah, big hole rate there would suspect why all of a sudden in grade six on our standardized assessment, which does have rate problems and proportion problems. No wonder we’re getting killed on that jugs of milk problem.

Kyle Pearce: Absolutely. And even if all of those things weren’t working against students, in our case anyway, it is like one of those muddy areas anyway. So, it’s like double compounded here where we’ve got a bit of a double edged sword working against us where we’re missing some of those resources, maybe that awareness, but then we also have a bit of that confusion and we talked earlier in the episode about the two types of division. I don’t know if I want to drop this on everybody right now, but when we look through this roadmap, part of that roadmap is this idea from spatial reasoning and doing comparisons spatially to doing measured comparisons like through counting.

Kyle Pearce: And then we moved to additive thinking and multiplicative thinking. Then and only then can we get into this land of actual multiplicative comparisons where we start to name these comparisons as ratios and then in some cases we can think of the ratios as rates. And as we work through this roadmap, there’s all of these hidden, I’m going to call them treasures. I know it might feel stressful to people, maybe they’re like, “This is not a treasurer at all. This is actually like a horrible thing to find out.”

Kyle Pearce: But when you get to that additive stage and you work with addition and subtraction and you realize that, “Oh my gosh, not only are there two types of division, but there’s also more than one type of subtraction.” That is always a mind-blowing one for educators as well and different ways to look at it. But typically, we’re telling kids things along this roadmap, along this journey and we’re not telling them the whole story. So, when we say division is this, instead of it can be this or this, or when we say, “Hey, when we’re subtracting, subtraction means take away.” Well that’s actually not always true because we can also look at subtraction as comparison.

Kyle Pearce: We could say, how much more money does Jon have been me? I’m not taking anything away here, I’m just comparing your $80 to my $40. And although I can remove my 40 from your 80, it’s not really removal that’s happening. It’s more of a canceling process. Or if you pictured on that number line, it’s like a jump on the number line between the end of my quantity and the-

Jon Orr: It’s a space. It’s a distance. Right?

Kyle Pearce: And yours. Absolutely. It’s like the distance, that difference between. And we could look at missing subtrahend problems. And all of these things that are hidden in the background, this is a lot of stuff for us to try to know just out of the box, because we don’t all have math degrees. And even if you do… I know Jon, you have a math degree and I do as well and I thought subtraction was takeaway, but there’s more than one scenario. I just thought it was one thing. So, this is like what our journey has been for the past little while, is trying to build our own content knowledge as we try to muck through this.

Jon Orr: So, it sounds like we’ve talked a little bit here about why our students are struggling with proportional reasoning. We’ve given some background on where that might be coming from. So, why this concept is holding our kids back. But so let’s dive into, it sounds like the tip you want to give teachers here on this episode is, one, thinking about this proportional roadmap, being able to dive yourself into some of the learning on what those steps look like, being able to name them when you see them, and then know where the kids are coming from.

Jon Orr: So, if you’re teaching grade four, know what they’ve been exposed to in the past on the curriculum guidelines. Have they been doing? For sure, most people have been doing the spatial comparing, you’re doing that from early, early ages. Like your example, Kyle, we talked earlier tonight about being able to say I can walk through this door, I can spatially see myself go through that door, which is an unmeasured comparison and then moves into a measured comparison.

Jon Orr: You’ve just talked about some additive terms and some multiplicative terms, but this roadmap that you’ve put together here is quite helpful for teachers. And I think one big tip for our teachers here on this episode is to know the roadmap so that you know where your kids are coming from, where they’re going to be going and knowing the terms and the different kind of levels of the math behind this proportional reasoning. I think that can be very, very helpful in moving forward to strengthening the proportional relationships in your own students. Well, what do you say, Kyle? Do you want to talk a little bit more about this roadmap?

Kyle Pearce: Yeah, and we’ll definitely at the end of the episode we’ll also be sharing a link for you to grab this little, we’ll call it like a roadmap cheat sheet. And we’ve done a lot of thinking about this over time and you’ll see all kinds of different scenarios out there. And I know Pam Harris, for example, and she’ll be coming up on one of the, I would say in the next five episodes, I think she’s coming up. And she talks about the road, or the thinking, or the continuum from counting all the way to proportional relationships.

Kyle Pearce: Here this is something very similar, but we’ve broken it down a little bit more granular based on teaching elementary and middle school mathematics developmentally. So that’s like a Vanderwall book and all of his wonderful colleagues as well as the student continuum of numeracy development by Alex Lawson. That was something that I looked at myself and Yvette Lehman looked at to gain a better understanding of where this all intersects. And at the end of the day really it’s just to provide a roadmap for teachers to be able to start where they are.

Kyle Pearce: So it doesn’t mean you have to start right at the beginning. You can start in the middle, you can start wherever you think that your interest lies. So like if that division conversation got you really interested, then you probably want to be hanging out or at least thinking about that multiplicative stage, right? Somewhere in there and going, okay, what’s going on here? But then you’re going to find that no matter where you start, you’re going to start wanting to go up and down to try to see how it all connects. And you’ll notice that, oh my gosh, all of this stuff is so important. And it’s not important to memorize. It’s important to get this understanding of how it all connects. And really you start seeing it everywhere and you start to bump into scenarios where you start to wonder to yourself like, “Where would that fit along here? How is it connected?”

Kyle Pearce: And really, everything is connected. And I would argue that this is probably one of the most important continuums or trajectories that we need to be focusing in on because it has so many implications both in early math, but then also as we move into more complex concepts, like for example, trigonometry, it’s all based on proportional relationships, right? And linear expressions, we’re building off of this idea of proportionality. And so, these are all things that we’ve spent a lot of time and really we’ve had so many people go through our online workshop who also want to dive deeper into that content knowledge.

Kyle Pearce: So we’ve actually put together a full course that’s nine modules together that we’ll be sharing some details in, I would say what probably three to four weeks time when this goes live about how people can learn more about diving deep into this particular roadmap so they can build that content knowledge.

Jon Orr: For sure. For sure. One of the other tips I think we can give teachers here is going back to this idea about one of those, the models with legs or the power tools. And this is something that really helped me, Kyle, and then I know that you helped shape this for me, and this is how I moved away in my ninth grade class when teaching proportions to our grade nine applied students. I was teaching that procedural way and the step-by-step let’s do this, let’s do this, let’s do this. And then with talking with you and the learning that you’ve been doing, we moved all of that to a double number line.

Jon Orr: And that double number line of representing proportions, representing ratios, fractions, solving equations, it’s all been really connected to that number line and it’s such a useful tool that you can move through the course with, move through these connected ideas and represent so many things on that double number line to help solve problems.

Jon Orr: And I really grasped to it when we represented just some basic proportion work on it when you’re solving a proportion. You don’t have to set up the unknown to be in the numerator if the unknown is in the denominator because it’s on the bottom of the number line, it doesn’t change anything in that solving of that proportion, which is awesome to show students. Like you don’t have to set this up, and then divide by this, and then multiply by this. It becomes pretty awesome. And then when to compare it with unit rates is built rate into using a number line.

Jon Orr: Solving equations on the double number line became very nice. Seeing when a linear relation was a direct variation or partial variation that gets clear on the number line when that occurs. So, I’ve always appreciated you sharing some of those models with me that has shaped how I do proportional reasoning in those classes. Now I’ll never go back because I think it’s such a visual model but also helps you with the conceptual understanding between the multiplicative relationships between the numbers.

Jon Orr: I think one of those key pieces, and I think if there’s only one thing that you take away from this episode I think is what you just said there, Jon, I hope people are hearing this idea that if we go to mathematical models and we build them in, and you can’t bring them all out all at once, you can’t learn them all at once, but if you pick one to at least start learning about yourself and then starting to figure out how you can incorporate it into your practice, and then building more in over time, what it really allows you to do, like I was picturing as you were talking about that double number line. I’m picturing one of the main things that bringing math models, these visual math models, into play is it allows students to reason through the math instead of just relying on steps and procedures like we were so used to doing and just so accustomed to teaching our kids.

Jon Orr: So, to me, it’s like if we can get our kids’ reasoning, that’s such a great place to start. So, if you haven’t started that journey yet, why not think about doing that and just that right now. You could even Google double number line, you’ll probably land on some of the things we have out there as well. But just to get yourself started. And for those who are interested to take this cheat sheet with them, we will be offering that for you.

Jon Orr: If you head to makemathmoments.com/proportion, that’s makemathmoments.com/proportion you can grab that PDF, grab a copy of it and use it as just a place to get your head thinking about what’s going on along this trajectory. Whereabouts are my kids in my room? If I’m teaching grade one, for example, where are they? They’re probably more in that spatial, to counting, to additive stage, right? Somewhere in that zone. And some students are going to be struggling in that additive stage. And as we go into the grade three and four classroom, we start to see, well we want kids to be moving into this multiplicative stage.

Jon Orr: And you start to realize, “Ah geez, some of the kids are spinning their tires in the additive stage still.” So by giving yourself a starting point to get an idea of where along this roadmap are students spinning their wheels? That might be a great place for you to start thinking about how you can dive deeper a little bit on your own professionally and work with the colleagues in your buildings so that you can start developing a deeper understanding of proportional reasoning in general, but then also how it impacts and influences where students are along that particular trajectory.

Kyle Pearce: Awesome stuff. Awesome stuff. I think those are some great tips for our listeners here. And in this episode we’ve really hoped that we’ve shown you why our students are struggling with proportional reasons, where that has come from, the history there, how we can help our students. We’ve hoped we’ve shown you or given you some tips on how you can help your students from various grades and also how you can develop a deeper understanding of proportional reasoning so that you can get that deeper understanding for your students.

Kyle Pearce: If we’ve done any of those things, give us a thumbs up right now wherever you are. Some people are probably looking at you weird if you’re just giving thumbs up in the middle of wherever you are. Say you’re cutting the lawn and you’re just giving a thumbs up to the sky. People might be laughing at you, but do it anyway. Come on. So yeah, we’ve hope we’ve helped you here. Thanks.

Jon Orr: And thanks for listening in on this master class.

Kyle Pearce: Yeah, we’ve had a blast there, Jon. I hope everyone’s enjoyed this conversation about that concept that’s holding our students back. And I know for me for many years was holding me back. Again, very hard to go in depth into all nine modules from our course. But we will be giving you some details in the upcoming episodes about how you can take advantage of diving deeper if you so choose with us in the Math Moment Maker community. But as always, both Jon and I learn so much from all of our conversations together, but in order to ensure that we hang onto new learning, you’ve got to reflect on what you’ve learned.

Kyle Pearce: So, an excellent way to do this, to make sure the learning sticks is to reflect and create a plan for yourself to take action on something you’ve learned. Is it going to be exploring a part of this proportional reasoning roadmap? Is it going to be thinking about the two types of division or those different subtraction structures? What’s it going to be for you? Make sure you write it down, make a plan, and take action on something that you’ve learned.

Jon Orr: You can do that also by tagging us @makemathmoments on social media or in our free private Facebook group, Math Moment Makers K-12, hit us up in there with some messaging.

Kyle Pearce: In order to ensure you don’t miss out on new episodes as they come out each week Monday mornings at 5:30 AM Eastern time, make sure that you hit that subscribe button. Don’t just hit it, smash that subscribe button on your favorite podcasting platform.

Jon Orr: And be sure to smash that five star rating button as well and leave us a quick sentence or two in that review box. Each of these reviews help us gain a wider audience so that we can make Math Moments worldwide.

Kyle Pearce: Awesome stuff. Show notes and links including the link to the roadmap cheat sheet from this episode can be found at makemathmoments.com/episode, 65 that’s makemathmoments.com/episode 65. Well, until next time, my name is Kyle Pearce.

Jon Orr: And I’m Jon Orr.

Kyle Pearce: High fives for us.

Jon Orr: And high fives for you.