Pam Harris: I think many of us look at the standards. And no matter where you are, your standards are fairly like the Common Core. Sorry, if you’re one of those states that doesn’t think they are. And so if you look at whatever standards you’re supposed to teach, I think a lot of us think I’m a seventh grade teacher, I’m supposed to teach these content standards instead.

Pam Harris: What if our imperative, what if our mandate was to create, to develop mathematicians, to develop students who did the math practice standards, who lived the math.

Kyle Pearce: You’re listening to today’s guest on the making math moments that matter podcast. It’s Pam Harris. Pam is a former high school math teacher, turned math consultant living in Austin, Texas. When she’s not teaching pre-service teachers at Texas State University, she’s out and about leading K through 12 mathematics professional development sessions, writing books, and leading courses.

Jon Orr: We’re eager to share this fantastic conversation with Pam about what it means to do math, defining the end goal when teaching a concept, discussing the difference between models and strategies, and why math is figureoutable.

Kyle Pearce: I think we are ready to dive in with this conversation with Pam Harris.

Jon Orr: All right, let’s go.

Kyle Pearce: Welcome to the making math moments that matter podcast. I’m Kyle Pearce from tapintoteenminds.com.

Jon Orr: And I’m John Orr from mrorr-isageek.com.

Kyle Pearce: We are two math teachers who together with you the community of math moment makers worldwide who wants to build and deliver math lessons that spark engagement, fuel learning, and ignite teacher action. John, we’ve been waiting for this episode with our good friend Pam Harris for quite some time.

Jon Orr: Of course, Kyle, of course, we are super pumped to bring you this episode as always, and you know what is fantastic? Opening up Apple podcast and seeing a brand new five star rating and review from the math moment maker community.

Kyle Pearce: Just like this five star rating and review from MW Math Sy, “Always gives me something to reflect upon. I’m so enjoying this podcast, great variety of shows, and there has been at least one nugget in each show that really gets me reflecting on my own practice. Even after three decades in the classroom, I like to see what I can do better.” That sounds like a typical math moment maker over there. MW Math Sy, thank you so much for leaving us that five star rating and review on Apple podcasts.

Jon Orr: Yes, Kyle, we want to thank our fantastic math moment maker community like MW Math Sy who took the time to help ensure the podcast reaches the ears of more math teachers around the globe.

Kyle Pearce: Well, my friends who are listening at home, go ahead. What are you waiting for? It only takes a minute to fire us an honest rating and review. Grab that phone, pull it out of your pocket, and go ahead and do it right now. As you’re listening, it means so much to us.

Jon Orr: Also, you’re clearly interested in getting kids leaning in to learn during your math lessons with the goal of building of conceptual understanding, number fluency, and a flexibility. Well, how do we know? Well, you’re listening to a math podcast, of course.

Kyle Pearce: Want to take a dive into the make math moments three part framework? You can download our three part framework guidebook by visiting makemathmoments.com/framework.

Jon Orr: In this downloadable ebook, you’ll be able to take the learning with you and build your own understanding of how you can spark curiosity, fuel sense-making, and ignite your teacher moves in all of your math lessons.

Kyle Pearce: Go ahead and grab it now by visiting makemathmoments.com/framework. That is makemathmoments.com/framework.

Jon Orr: Okay. Now onto our chat with Pam.

Kyle Pearce: Hey there. Pam, welcome to the making math moments that matter podcast. We’re super excited to have you on the show today. How are things on your side of North America?

Pam Harris: Hey, Kyle and John, I’m thrilled to be with you guys. Thanks for having me. Things here are cold at the moment, but we’re doing well.

Jon Orr: Awesome. Awesome. That is fantastic, Pam. You know, we’ve met a number of times, but like always, we’d like you to just fill our listeners in a little bit about yourself. It’s possible that they might not know who exactly you are. So, could you fill us in a little bit about your role in education? Where are you coming from and how did you get into teaching and education? Fill us in a little backstory for us, please.

Pam Harris: So at the moment I’m in Austin, Texas. I teach Texas State University. But honestly, what I do the most is a lot of professional development. I work with pre service teachers at the university, but I do a lot of inservice professional development with teachers around the country. Keep hoping to get to Canada one of these days.

Jon Orr: We’d love to have you, come on up.

Pam Harris: I do a lot of work K-12. I began as a high school math teacher. I had a great time teaching high school. I love teaching juniors and seniors. They made me happy. Freshmen made me slightly crazy. Really enjoyed teaching. I’m going to date myself just a little bit. When I began teaching, graphing calculators had just come out and in my student teaching experience-

Jon Orr: The TI83s?

Pam Harris: The TI81s.

Jon Orr: Whoa. Well, if it was the first one, would it be like the TI1 or something like that?

Pam Harris: I actually started with the 81, very first one I used was at the university. There was an HP calculator that my professor said, you could use it if you wanted to, but you didn’t have to. We were at a complete disadvantage. Those of us who were taking linear algebra, who didn’t have it, as my boyfriend at the time actually had one.

Pam Harris: He took about 38 minutes on the first test and I took three and a half hours because I did all the computation by hand.

Jon Orr: You probably got more out of it though, right?

Pam Harris: So let’s talk about how to teach with technology. If you’re going to teach with technology as a tool, you have to be aware of the assessments that you give because you could definitely put students at an advantage or disadvantage, especially if you give them a choice whether they’re going to buy that expensive tool or not.

Pam Harris: So, because I landed in my student teaching, Pam Giles was an amazing teacher. She was one of the very first teachers who’d ever taught with graphing calculators. She went back to the Ohio State University with Frank Deman and Burt Weights. They were the professors that were sort of the grandfathers of graphing calculators and really learned how to teach math using the power of visualization.

Pam Harris: I give her a lot of credit for my beginning years as a teacher, so in a huge way that student teaching experience flipped everything on its head and I learned there was a better way to teach math than the way that I was taught. I could play with the math. I could play with… I’d never heard of a parent function before. I never heard of transformations. And all of a sudden I could put a trig function in there and I could mess around with the parameters and I could see what happened. It was so much fun to just play with the math. And it really opened up my experience to a different way of thinking and reasoning about secondary math.

Pam Harris: So I’ll tell a short version of the story. I had four kids, my own personal children, and when they were growing up, I was fascinated by the kind of math they were doing. We just messed around with numbers a lot at home. We bake together and count it a lot and play some math games. And my personal children were just messing with numbers in a way that I never really had and I just became really fascinated by it.

Pam Harris: The short story is I started volunteering in their classrooms because I noticed that the math they were sort of doing with me was really interesting, exciting, and they were really thinking and reasoning, but they were bored in school. I knew that there was a better way to teach secondary math. I learned that with graphing calculators. I began to wonder if there was a better way to teach arithmetic. And so I’ve volunteered in schools, dove into the research about how we could teach arithmetic better, and learned that indeed there is a better way that we could teach kids to really have powerful numeracy. And I give my own personal children a lot of credit for that.

Pam Harris: So I learned that. Like I said, I volunteered on my kids’ classrooms. Over a period of about five years, I kind of took over my kids’ school. I did all the professional development with the teachers, K-5. And then as my kids grew up, I did the professional development K-8 and my kid’s district, we had about 13 elementary schools. Honestly, we made a lot of mistakes. We sort of dove in and tried some things that I, as a secondary teacher, I thought, oh, everybody must know this stuff. But what I didn’t know is I had landed in some research that was really quite new.

Pam Harris: And so we tried a bunch of stuff, learned a ton of things. At that time, I had been working with Texas Instruments. Because my cooperating teacher and graphing calculators, and so I was also doing PD around the country teaching teachers how to teach high school math better with graphing calculators. While I was really building my own numeracy. I was learning that I hadn’t had any numeracy.

Pam Harris: Like sometimes I’ll joke a little bit that I had negative numeracy, and so when I was doing the PD with graphing calculators at break, I would say to my fellow secondary teachers, hey, did you know you can actually think about subtraction? And they were, for the most part, surprised and intrigued and kind of interested, and teachers began to tell me, you know, we would go to a workshop on that. So I kind of began to give my own workshops on building powerful numeracy. Some of those beginning workshops, I look back and man, I really didn’t know. I would ask teachers a question. I would say, okay, how do you solve this problem? And then I would really have to think to be able to understand.

Pam Harris: And often now I use a PD move, a teacher move, where I’ll ask people to restate someone’s strategy. Or if somebody could explain… if Kyle had given a strategy, I might say, John, could you explain Kyle’s thinking? Or could you restate his thinking? But in the beginning days I had to do that just so I could understand Kyle’s thinking. There’s like, I had no idea really what people were doing because I was literally building my numeracy along with people at the same time.

Pam Harris: And so in that work, I began to basically spend about the next 15 years traveling around the country talking about building powerful numeracy. And so I wrote a couple of books, did tons of workshops for numeracy, and I’ll just kind of finish up my story a little bit by saying that about eight years ago, I turned my attention back to secondary math and I realized that there were some things that I’ve learned in building and teaching numeracy that I could actually apply in teaching higher math. So when I was talking about building powerful numeracy, often the workshops I gave for secondary teachers were if we could build some numeracy in your secondary students, then look how that will help you teach the content that you’re actually supposed to teach them.

Pam Harris: We did a little bit of subtraction into the slope formula. Wow. Kids actually understand, but it’s the difference. That’s subtraction sign in the slope formula has everything to do with the distance between those Y values. The distance between those X values has nothing to do with takeaway or removal. And so I was doing all this numeracy work into high school content or middle school content, but then I turned my attention back and I actually realized that there were some things I learned in teaching elementary math that I could now apply in teaching secondary math, like lesson structures, ways of teaching, ways of interacting with students, high leverage teacher moves.

Pam Harris: And my favorite lesson structure that I learned is kind of the one that I champion now, it’s called problem strings. A lot of people think they’re like number talks and it add some elements that are similar to number talks, but in a huge way they are I think the inroad for teachers. I think if teachers are interested to change their practice more towards real math and the thinking and reasoning, using relationships, what I call real math, I think problem strings could be the place for teachers to start.

Pam Harris: And so for the last few years I’ve really worked hard on writing problem strings for middle and high school teachers really with like high school content, algebra problem strings, geometry problem strings. And I also worked really hard K-12 on sequencing tasks. So that’s another interest of mine is how can we take things like problem strings and number talks and rich investigation, rich tasks, like three act tasks and how can we sequence them?

Pam Harris: I think rich tasks are cool. I think number talks are neat. But I think really when we can put them in concert with each other, when they work together, that’s really where the power comes in and we really can help students develop as mathematicians.

Kyle Pearce: That is quite the story. I’ve taken down some notes and I know through our conversations, and actually recently, spending some time at the NCTM regional together and having a chance to really sit down and grab a bite to eat over lunch and just chat about math. I see so many of the same experiences you’re describing that have been happening to me maybe more recently because again, folks who are listening, they know John and I both came out of the secondary classroom. John’s still in secondary classroom and I’m geeking around K-8 a lot. And even recently, we just did some workshops last week. And when you bring up this idea of takeaway or removal, subtraction versus the difference or the comparison subtraction, we actually did a Cathy Fasano mini lesson with our PD group highlighting that and just in how sometimes even the values we’re working with will sort of like lend to certain strategies.

Kyle Pearce: And this one particular mini lesson was really cool for those who are listening. You know, if you were to think about how you would subtract 74, subtract six. If you think about 74 subtract six, typically what people tend to do with that is they tend to think of it if it’s no context, right? If the context is there, then you sort of tend to ride the context as to whether you’re actually taking away or you’re doing the difference.

Kyle Pearce: But in that case, people tend to take away, because you’re only taking away six. It’s like it’s pretty easy to do. You know? I could take away four and then two. And boom, we’re good to go. But then when we look at larger numbers, when we’re subtracting like 86 minus 78, while you can take away 78, it’s a lot more work.

Kyle Pearce: And what people tend to do, not everyone, but what people tend to do is when the numbers are closer together, they tend to think of it as a comparison or a different subtraction versus a removal or takeaway. And a colleague of mine, Yvette Lehman, she says she has to like deprogram her son who’s in kindergarten because he thinks subtraction. When he sees that symbol, he thinks takeaway, and there’s actually more than two types of subtraction. You can also think about missing add in and missing subtrahend problems as well. But for him, he thinks everything’s takeaway. And in reality, there’s this whole other world of comparison, subtraction, or the difference, finding the difference between two values. And for me that really resonates and I’m hoping we can keep diving into your journey here.

Kyle Pearce: I think I’m going to really geek out on this one because I realized as well, I had very little. I love your expression of negative numeracy. I had very little, I was a memorizer and I could calculate whatever you threw at me, but I didn’t really have a strategy. I couldn’t articulate my strategy. So I think we definitely connect on that level. So before we go any deeper though, I want to go and dig back. You’ve given us an inside scoop as to your own professional learning journey as a mathematics educator and now consultant. I’m wondering if you can roll back to your experience in math class. Is there a memorable math moment that sticks out for you when you think back to math class?

Pam Harris: You bet. I’ve got a couple, but I’ll share this one with you. I was in seventh grade. I had no friends. I looked around and I thought, I’m good at math. I’d always been good at math, which for me at that moment meant I had been quick, I memorized well. I sort of went around the world in third grade. I was the first to do long division in fourth grade. I didn’t really know what I was doing. I definitely couldn’t articulate why it was doing what I was doing, but I was able to mimic the teacher well, what I now call fake math. I sort of knew I was good at that. And I looked at the math club. There was a math club that met, didn’t know before.

Pam Harris: I saw that’s a place I could go belong, sweet. Maybe I could find some people I could fit in with. I’ll go to the math club. So I went to the math club. The kids were already sort of working on some things. I sat down and coach handed me a piece of paper with some problems on, and I looked at the first problem. I’ve never seen the first problem. I had no idea how to do it. So I skipped the first problem into the second problem. I’m seeing a pattern, I didn’t really know how to do any of them. I knew how to play the game. I know what you do in math class. So I raised my hand. Coach came over. I said, hey, you know what?

Pam Harris: I’ve never seen these problems before. If you wouldn’t mind, if you just teach me how to do these, then I’ll happily solve them correctly. And I know how to play the math game. And he smiled at me and he said, oh, you know, that’s not what we do in here. We just sort of use what we know. We kind of play around with the numbers, and we solve a problem.

Pam Harris: His description of what I was supposed to do to solve those problems was so foreign to me. It was so different than my experience in sort of school fake math. I didn’t know what to do with it. I kind of looked around the room. I was so uncomfortable. I stood up, walked out, never came back. I just put it out of my mind.

Pam Harris: I thought, well, whatever that was, I didn’t understand. They’re weird and I literally just didn’t really know what to do with it, so I kind of just ignored it and went on with my life. It’s so interesting for me now to look back on that experience and realize why that was so different for me and what I could have done in that math club really was just think and reason and use what I know. But in a huge way, I wasn’t able to hang onto relationships until, and I’m going to give a lot of credit to Kathy Fasano and her young mathematicians at Workcrew. You’ve mentioned earlier that you guys were using a mini lesson from her work. When I mentioned that I dived into elementary research that had just come out in a huge way, it was her stuff and reading a lot of the research that she and [inaudible 00:17:59] had put out. A lot of it is based on the idea of making thinking visible, of helping students take up thinking because they’re using powerful visual models to represent the relationships visually.

Pam Harris: I had had teachers before. Here’s another memorable moment for me. I was in eighth grade and we had just learned how to foil. So we were doing linear binomials times each other, multiplied by each other, and the teacher had taught this foil thing. Well, then she was absent the next day and had a substitute, Mrs. Newburn, I will never forget, said to me, “Hey,” she kind of knew that I liked math.

Pam Harris: She said, “Hey, you know, you could use this distributed property that you’re doing. You could use that to multiply numbers together.” And I looked at her and I was like, whatever weirdo, like I don’t know what you’re talking about. I remember that moment because she was so excited about it and I had so little access to what she was talking about. I knew that math was about memorizing. It was about mimicking the teacher and spitting stuff out. And so when she tried to tell me another way to get an answer, I had ways to multiply. I knew how to multiply, multiplied well, and multiplied with the best of them. And so when she says, you know, you could multiply a whole numbers using this other strategy, to me that was like, I’ve got a way to do it.

Pam Harris: If math is all about rope memory, then I’m trying to shove it all in my head. If you could see me right now, I’m like plugging my ears because if it’s about rope memory, why would you give me extra. That’s like mean. Ff I have one way to do it, don’t try to put more in my head. It’s going to start leaking out one of my ears. I can only hold so much in there at a time. But what I didn’t realize is what mathematicians do. Mathematicians use what they know. They use the relationships among the numbers. And in a huge way, I was finally able to start doing that when those relationships became visible, when I could start seeing an open number line and I could put numbers that I needed to mess with on the open number line.

Pam Harris: And I could say to myself, what are friendly numbers near these numbers that I could use or an open array, an area model, if I was going to work with multiplication that I could really sense the chunks of numbers that I’m dealing with area. The area to me as a student meant, wait, is that the one where you multiply or you double and add? Because I had completely known that there was finding perimeter and there was finding area and I just needed to kind of remember which formula was which. And then I was done with area and perimeter. Oh. But I could actually use an area model to really think about relationships with multiplication. And by doing that, then I built my multiplicative thinking and building my own multiplicative thinking just opened up the whole world of proportional reasoning and functional reasoning that I can actually use other relationships to solve more and more complex problems.

Pam Harris: The more relationships I was able to take up because they were made visible, the more that I was able to use to solve other more complex problems.

Kyle Pearce: It’s so funny because you’re trying to memorize all of this stuff, like I totally can relate and I find that there’s a lot of students that we tend to consider to be quote unquote math people. And they have that same perspective as well, and it’s likely that they just got kind of lucky that they’re able to memorize things without actually having a connection. Like they have that rope memorization and they don’t necessarily have that automaticity, like actually being able to reason and problem solve and actually use it for different problems that they haven’t seen before.

Kyle Pearce: And you know, it really reminds me of what we might hear when a teacher shifts from this traditional method of teaching, like essentially more of a traditional style that maybe most parents and folks that are our age actually experienced as students. We tend to hear things like I don’t understand this new math. I don’t get what they’re doing. They’re complicating things. Like there’s even videos on social media where I saw one recently, it was like side by side of a teacher trying to show connections with multiplication, with the area model. And then on the right, the guys using the standard algorithm and he’s done in like 13 seconds.

Kyle Pearce: And then it shows him like cooking things in the microwave and like doing all this other stuff. And really just basically giving this impression, like you had said, that it’s like my only job here in math class is to gobble up all of this information and regurgitate it, and I can’t actually take on anything additional.

Kyle Pearce: And actually in that sort of learning environment, I would agree that actually they would get confused because they don’t understand what they’re doing anyway. So I’m wondering. What do you say to a teacher who has that? I know what I might say, and I know John, you’ve had this discussion before too, like what would you say?

Kyle Pearce: What would Pam Harris say if let’s say a teacher you’re working with in PD is saying, I’m fearful that a parent’s going to push back on what I’m doing and that their kids getting confused? And it’s often like a frustrating sort of experience moving from that traditional model to a more conceptual model.

Kyle Pearce: I’m wondering like what are your thoughts on that? How might you help someone who is trying to ditch that procedural rote memorization without connections sort of method to something more conceptual with connections and reasoning and problem solving.

Pam Harris: Yeah. You bet. If I could actually first talk just a little bit about that social media video that many of us have seen. I actually think one of the problems with that video is less sort of the guy on the right who does the algorithm and then goes and gets a cup of coffee and puts them in… all the stuff that he does. But actually the thing that’s on the left with the area model is actually, if it’s the version I saw is also fake math. It’s someone who’s using the area model in a very procedural step-by-step way. I actually just saw a tweet today where someone was sort of saying, yay, look at how I’m doing conceptual stuff in my math class. But when I looked at the pictures that were in the tweet, I saw a student multiplying seven times a two digit number.

Pam Harris: I don’t remember what it was, but had drawn a four by four square and had written zero seven as the dimensions on one side and then whatever the other two. In other words, the students sort of splitting by place value. Memorizing this way to use more of a graphic organizer instead of actually what would a seven by 23 look like? Well, it wouldn’t look like a square for heaven sakes. It should look like something’s short, something much longer 23, and then why would I ever consider zero plus seven. That’s the two chunker. That’s a seven by 20 in a seven by three. I could add those together.

Pam Harris: So whenever I see somebody using an area model as just another procedure another thing to memorize and a good clue is if kids have written seven to zero, one dimension, then I’m also going to push back against that. It’s not about the model. One of the things I try really hard to help parents and teachers understand is that it’s not about the open number line. It’s not about the open rates. What we’re doing with them. If I say to a student, Hey, how did you solve that addition problem? And the student says, hmm, I did a number line. Then I’m going to smile and I’m going to say, what did you do with the number line? What numbers did you use? How were you using relationships to solve the problem?

Pam Harris: It’s not about the number line. Often, we’ll ask students how they did a multiplication problem, and they might say, I did a ratio table. To which again, I’ll sort of grin and I’ll say, what did you do with the ratio table? So differentiating between models and strategies and helping teachers realize that there’s a difference between those two is one of the most important things that we need to help teachers who want to take that jump that you’re talking about. We need to help them understand. It’s not about just taking a new picture and applying now a new set of rules to a picture. I mentioned earlier that the visual representation is important, but the visual representation should be of the relationship students are using, not of just another set of memorized steps.

Pam Harris: So another thing that I think is really helpful in this conversation is the difference between a strategy and an algorithm. I just actually talked to a fairly highly respected secondary PD person the other day in Salt Lake, actually not too long after I talked with you, Kyle. And he said something about, well, if a student creates their own algorithm, they use these relationships and they’ve sort of created their own algorithm.

Pam Harris: I’m going to have to pause right there for a second. Students rarely create an algorithm. So let’s define algorithm and strategy real quick. An algorithm is a series of steps, a step by step procedure that’s designed to solve any problem in the class. What that means is it’s a generalized procedure. It’s all the steps all the time. It is the thing that computers must have. Computers have to have algorithms because they have to just shove the numbers in and do all the steps all the time because computers cannot be judicious problem-solvers. Computers can’t look at the numbers and let the numbers influence how they’re going to solve the problem.

Pam Harris: For example, if I were to add 99 plus anything, I don’t know. Pick an ugly digit, two digit number. 99 plus 47. If we were going to add 99 and 47, a computer with line those numbers up, just like we all learned in first grade, would work with the digits first, would regroup the numbers as they go right to left, small to big, because the computer has to do that.

Pam Harris: But if you get anybody with numeracy or any kid before we’ve sort of ruined them by stressing the traditional algorithm. If you ask any kid 99 plus 47, a lot of people, when I do that 99, I sort of activate some prior knowledge. I activate this idea that you’re inclined to go 99, 100. Well, if you’re thinking about 99 and 47 is 99, 100, you still have to add. You were supposed to add 47, but you’ve already added one, so you still have 46 left. Now, really wish I’m showing this on an open number line so we could hold on to these relationships better, but 99 plus 47 simply becomes a hundred, plus that left over 46. Well, 146, that’s pretty doable.

Pam Harris: That’s an example of a strategy. A computer’s not smart enough to choose to do that strategy. That’s far more efficient than using the traditional algorithm to add 99 and 47. And let me go a little further. An example of the traditional algorithm for multiplication. If we were to do 99 times 47 for multiplication, we would have to do all the steps all the time, including the magic zero and all the addition and all the things, and it would take quite a few steps to do 99 times 47. Let’s activate that prior knowledge one more time. 99, 100. Could you think about 99 47s as 100 47s. If I’ve got 100 47s, but I only want 99 47s, I just need to get rid of 47. So now I need to know something about 4,700 minus 47 and we’re maybe back a little bit to what we were talking about earlier with subtraction, how important subtraction is.

Pam Harris: To really understand and be able to feel. A quick story. I was actually at a math conference several years ago. The math focal points had just come out, and a lot of people recognize them because they were kind of short-lived and we didn’t do a lot with them here in the states. But NCTM at one point had funded the writing of the math focus points. And one of the authors was a good friend of mine, and we hadn’t just never had this conversation. And so in the middle, she’d given a presentation on the math focal points and in the middle of presentation they had a question and answer. And I raised my hand and I said, my question for you is, why did you put so much emphasis on the traditional algorithms in the focal points?

Pam Harris: And she glared at me from across the room because she knew I was bringing up kind of a hot topic. She gave a fine sort of politically correct answer. And then we were done. And she came up to me after the session and she was a little frustrated with me. And she said, why did you do that in front of everybody?

Pam Harris: And I said, because I really want to know, like I’m actually really interested, why are you putting so much emphasis on the traditional algorithms? And she said, well, Pam, your secondary, you know as well as I do that there are times where you just want to do the quick and dirty thing to get the answer. To which I replied, 99 plus anything, 99 times anything, and I’ll never forget. We were kind of walking down the hallway in this very busy math conference, very busy hallway, all these people, and she stopped. Several people ran into us like, like piled up in the hallway. And she looked at me and she said, is that what those people are talking about?

Pam Harris: I thought that was so interesting. Here, we had a university person who was expert in her field who actually didn’t even really realize what a lot of us had been talking about. When we advocate children learning and developing alternative strategies, it’s not because we have some weird goal of just like getting them to kind of understand some things and then the goal becomes the algorithm. Here’s maybe where I differentiate myself from several people that I think are really good out there. They’re trying to accomplish really good things and I would differentiate my work from, like I said, lots of people that are doing good things, good work, really good work.

Pam Harris: If I described their work in a huge way, they’re advocating that we help students understand conceptually what’s happening with place value and numbers and relationships so that the students can then understand the algorithm better, but their end goal is a traditional algorithm. They do all of the learning and the thinking and the reasoning and the trying to help kids really estimate and get better at the relationships, but their end goal is still the kids then get good at a traditional algorithm. Not my goal.

Kyle Pearce: What is your goal then, Pam?

Pam Harris: So my goal is that I help kids become mathematicians. Now, when I say that, I pause a little bit because I’m realized that there might be people out there that say, Pam, Pam, I mean, maybe your students are becoming mathematicians, but you don’t know who I’m teaching. You don’t know my population. They’re not becoming mathematicians. I might have maybe two or three students that might someday become a mathematician, but caution. I don’t mean mathematicians to be, I want to mentor mathematicians in the here and now. I want my students to mathematize. I want them to actually do the work that a mathematician does at their grade levels.

Pam Harris: So if I’m working with freshmen, I want them to have ninth grade mathematicians. Sort of like when we teach kids to read, kids read. When we teach kids to write, they write. When we teach kids to do math-

Kyle Pearce: They calculate.

Pam Harris: We don’t have a verb for that. Right? So Kathy Foza coined the verb mathematize and I think mathematize means what a mathematician does when they are doing their mathematization. When they’re mathematizing, when the part of their brain that lights up, when they do their work. That’s the part of the brain I want to light up in my students. I want them to be thinking and reasoning, using relationships and connections they own. That’s my definition of real math. Not fake math. My definition of fake math is a disconnected set of facts to memorize and rules and procedures to… In fact, if I can just add one more quick thing.

Pam Harris: Often when I talk to teachers or when I hear teachers, they’ll say, hey, show me your work. If you show me your work, I will give you partial credit.

Kyle Pearce: Show me the steps [crosstalk 00:32:19].

Pam Harris: Yeah, I’ve given you the rule in the box. I’ve clearly shown you the steps. We’ve worked three worked examples, and now it’s your turn to go do. And if you will mimic my steps correctly, I would give you partial credit.

Pam Harris: Well, that’s not what I’m after. I’m not after the mimicking me. I’m after them learning the major strategies for each of the operations. This also differentiates me, I think, from a lot of people’s work is I’ve identified what I think are the major operations that students need to know for each of the… Excuse me. The major strategies students need to know for each of the operations so that they can solve any problems that’s reasonably solved by a calculator. They can quickly use one of those sets of relationships, and most of the time they will be more efficient than the traditional algorithm.

Pam Harris: Every once in awhile I’m as efficient as a traditional algorithm, but you know what? I’m never less, I am never less efficient than a traditional algorithm, and most of the time I’m more efficient. But even more important than that, I’m mathematizing. Like I’m actually using my brain and relationships to do what mathematicians do. It’s so empowering to know that I can think and reason using and what I know I actually own.

Pam Harris: I’ll take a breath. What are you guys thinking about?

Jon Orr: I’m just going to throw in a quick comment here. These big ideas that we’re talking about right now come down to what you just said a moment ago about what you want your students to think about math. Like most teachers think like what is doing math or what is being good at math mean?

Jon Orr: And so many of us just think like math is calculating. Math is getting answers and not memorizing, and like just doing the homework. Like we’ve talked about it here on the podcast before, that math is like the do subject. It’s like we’re supposed to just do this and then move on to the next thing. And you know, there’s such big ideas here to think about if we have a view of math as a just do subject and get done subject or do we have an idea of what you’ve said and suggested? Are we creating mathematicians? Is math about problem solving and thinking about strategies and coming up with their own strategies and becoming mathematicians? It’s a huge idea to think about and it’s such a huge mind shift that we have to help other teachers other teachers learn because we all were.

Jon Orr: We were those teachers that… I was that show me the extra credit, show me the steps, let’s get all this done and we’ll move on to the next piece. So it’s a huge mind shift for us to switch gears and think about math as not just getting these things done and memorizing, and doing math questions, but actually having our students develop strategies and use their own strategies or mathematize.

Jon Orr: It’s a huge thing that we’re talking about here.

Kyle Pearce: I can’t help but go back to this image in my mind. When Pam, you had mentioned this idea of like mathematizing in the part of the brain that you know is working. And on the other hand, I’m picturing like, do we want the part of the brain that’s working like the longterm memory only, like retrieval, like that regurgitating? And you had given some examples of the 99, 100 scenarios there and what strategies students might use. And like another big one that immediately popped in my mind was 1001 minus 999, right? Like talk about a complete mess that that is. If students literally are like, well, the only way I know how to subtract is to line them up.

Kyle Pearce: If I line them up wrong, then I’m toast. If I line them up right, if I borrow and I do something wrong here, I’m going to do a lot.

Pam Harris: Remember the nine versus the zero, right?

Kyle Pearce: Yeah.

Pam Harris: Zero sometimes and a nine sometimes.

Kyle Pearce: That ones such a doozy and it just immediately popped into my mind when you said 99 plus whatever. I was like, yeah, like it’s two apart, like it’s so close, it should pop right into your head. Something that happened to me actually today as we were sharing some… We had kind of like a monitoring assessment that we’re going to be doing like a handful of questions in our district to try to get a better sense as to where students are struggling with certain topics and like we’re routinely struggling with them.

Kyle Pearce: And we had shared a problem and we actually had a room full of administrators and they’re all great people and we’re all on this learning journey together. And something that really hit me and relates so closely to this conversation was when an administrator read the problem and then shared, bravely shared in the room that like the problem had the word difference and it had the word total really close together.

Kyle Pearce: And right away, the administrator had said like that’s probably why students are struggling. And like right away I addressed this very thing. Is that because students are looking for key words… Like, so I guess my question, and I didn’t state the question because obviously it wasn’t the appropriate time, but my real question, my real wonder is so what should we work on then? Should we work on changing questions so that keywords will still work for students, so that they can solve them? Or do we work on getting kids to become mathematical thinkers, to be able to mathematize this scenario? And if you actually look at the context of that problem as a whole, there was no doubt.

Kyle Pearce: Like there was no mix up as to what it was that they were having to do. And if they had that visual, as you mentioned, like the scenario would have been perfect for a number line and it was not a difficult problem, but it was like immediately going right for those key words. And then finally, I had this one on the tip of my tongue for a while, was talking about this idea of way back to that video on social media where what I see a lot of times and what you hear a lot of times as teachers start to begin shifting to a conceptual sort of approach. They tend to still think in that, I’m going to show you approach. So it’s like, I’m going to show you the area model versus Kathy Fasano. I know, you know this, is this idea of emerging models, right? So through students strategies, we’re going to actually emerge models.

Kyle Pearce: We’re not going to say like today, we are going to uncover the area model, and here’s how you do it. And here it is and you’re going to set this up. And that’s such a hard shift for educators to actually wrap their heads around. I’m sure you’ve probably got a bunch to say about that as well.

Pam Harris: Yeah, absolutely. So one of the things that I would share with teachers and leaders that are trying to make that shift. One way to think about it, I really wish I could remember who I’m quoting. I heard this about six months ago, and I honestly don’t remember who said it. So if anybody knows who it was, please shoot me an email. I’d love to be able to give them credit. But basically the idea is that I think many of us look at the standards. And no matter where you are, your standards are fairly like the Common Core. Sorry if you’re one of those states that doesn’t think they are.

Pam Harris: And so if you look at whatever standards you’re supposed to teach, I think a lot of us think I’m a seventh grade teacher, I’m supposed to teach these content standards. And I’ll teach them using the math practice standards. So my job, my goal, my imperative is that I need to teach these content standards, but I’m going to use the math practice standards, try to get my students to do some of those math practice things as I teach my imperative.

Pam Harris: I wonder about flipping that on its head. Instead, what if our imperative, what if our mandate was to create to develop mathematicians, to develop students who did the math practice standards, who lived the math practice standards. If we develop students who really were reasoning abstractly and quantitatively, and they really were making sense of problems and persevere in solving them, they really were modeling and using tools strategically and attending to precision and looking for and making use of a structure.

Pam Harris: If we really had students doing that. Oh yeah, that’s my imperative, my mandate, and how do I do that? Well, I’m a seventh grade teacher. I’ll use the seventh grade content to do that. Or I’m an algebra one teacher, I’ll use the algebra content to do that. Or I’m a third grade teacher, I’ll use the third grade content to do that.

Pam Harris: If our mandate or job, the thing that we really were focusing on was helping students do those math practice standards, become mathematicians, and how do we do that? We’ll use the content that’s our grade level or it’s our subject. Maybe I’ll use geometry because I’m a geometry teacher. I’ll use that content to help my students become mathematicians, who use those math practices.

Pam Harris: That’s a little bit of an interesting shift that I wonder if that might help some people realize more what we’re going for.

Kyle Pearce: For sure. It’s for most teachers done the opposite way, right? It’s kind of like I have my content standards to teach and then I gotta make sure I throw in an activity that gets kids to reason or communicate ideas and those kinds of things. So I think that would go a long way. And I think the teachers who have figured that out, Pam, are making the bigger difference in their students to get them to become those mathematicians and getting our students to actually think about math class. And then that makes the math moments matter for our kids.

Kyle Pearce: And I think those are the moments that kids actually start to remember about math class that are positive. It’s like, you’re going to get that kid later on, 5, 10 years from now, that says, you know what? I had a teacher that cared more about my learning than say, the content standards all the time. And I learned so much about just solving math problems.

Kyle Pearce: And I think that’s what we’re always gunning for. And that’s partly why we’ve created this podcast. And we’ve created our website and all those things we’re trying to help change. And I think that’s a great way to look at it. For sure.

Kyle Pearce: I want to keep going down this path cause we’ve been talking about so many huge ideas in mathematics and in mathematics education.And another one I think can come out of this is when I read your website, even just the title, like mathisfigureoutable.com, which is a great name for a site. We were curious about like where did you come up with this title? And then also if you think about somebody who has those negative mindsets about math education, like how do you believe or use the ideas that we’ve been talking about to help change some of those beliefs of how kids and also parents think about math. And it’s actually truly figureoutable.

Kyle Pearce: Can you just comment a little bit about the website name, where that came from?

Pam Harris: You bet. So often when I introduce myself, when I’m giving a presentation, I’ll start with math is figureoutable and then I’ll pause and I’ll kind of chuckle a little bit and say, of course, we all believe math is figureoutable. We’re all here in a math teaching workshop or a math conference. So, ha ha. We all think math is figureoutable. However, I’m going to admit that as a student and far too long as a teacher, I actually believed that math was rote memorizable. I believed it was a disconnected set of facts to memorize and rules and procedures to mimic, and I was good at that.

Pam Harris: So I liked kids and I wanted to teach and I went into teaching because of that. But now I have this whole different perspective on what real math is. Using relationships and connections you own to solve problems. And in the process, creating new math for the learner. That math really is figureoutable. And when I start a workshop with that sort of math is figureoutable mantra, it’s interesting. Usually somewhere around halfway through the day, someone will say, wait, wait, wait, wait. Something must be off. I’m really having to think here. Like I thought you said math is easy.

Pam Harris: I’ll chuckle a little bit and I’ll say, oh, hang on. I didn’t say math is easy. What I said is math is figureoutable. Yeah. It might take some thought. Teachers sometimes will push back and say, Pam, I could just quickly do that traditional algorithm and I could get that answer. I wouldn’t have to do all this thinking, my brain is really having to work to use these relationships and really have to put some mental effort into this. And I’ll smile and I’ll say, well, okay, so let’s just be really clear. What’s your goal? Is your goal to build your brain as a mathematician? Well, then I’m going to ask you to do some figuring. Math is figureoutable. I’m going to ask you to put that effort into it.

Pam Harris: Oh, what you’re saying is you just want to get a quick answer without having to think, is that what you’re saying? And people will sometimes smile and say, yes, I just won’t be able to do that algorithm because I can do it really without thinking at all. I actually had a woman tell me once, Pam, I can listen to you and I can multiply two digit numbers together and I can totally hear what you’re saying and not even put any thought into multiplying those. To which I reply, okay. If your goal is to get an answer without thinking, you know what? Let me hand you your cell phone calculator. If that’s your goal, if your goal is to be able to do something without thinking, then why not use technology?

Pam Harris: If you were an employee in a store and you chose to do something by hand where you could have done it with technology, you got to be fired. I mean, there are times where technology really is a tool for us, so I want to teach judicious use of graphing calculators or of calculators at all of, technology. Teachers often find it kind of interesting to note that I, on the one hand, do workshops on how we can use graphing calculators. Well, and on the other hand, I give workshops on mental math, because mental math number, I’m going to quote Kathy Foza here. Mental math does not mean that you do it all in your head. Mental math means that you do it with your head. Let me say that one more time. Mental math does not mean you do it all in your head. Mental math means that you do it with your head.

Pam Harris: So if you’re doing mental math and you need to keep track of what you’re doing to be able to sort of use those relationships, it’s totally legal for you to write down a couple of numbers or draw an open number line or whatever to help you kind of keep track of the relationships, totally illegal. But if you’re doing something in your head that’s a memorized series of steps and you can keep track of all those little ones and cross out, not mental math.

Pam Harris: Even if you didn’t write anything down, that’s not mental math. You were using what you know to solve the problem. You were mimicking somebody. That’s not mental math. That’s just mimicry. I’m not after mimicry or robots. I’m after creating, developing mathematicians.

Kyle Pearce: Absolutely, absolutely. And you know, John and I, we get this so often. When we get new strategies, it’s like trying to be told how to do something instead of actually figuring it out. Like when you’re actually in the workshop., I think one of the biggest challenges, and this happens too with our students who are comfortable with the game that they’ve been winning so far, right? We’ve actually been allowing them to supposedly believe that they’re winning the game of math because they’ve been blessed with like a really, really good ability to recall.

Kyle Pearce: And in reality, when we start to push them out of that comfort zone, it’s like all of a sudden they have no armor, right? It’s like, oh man, I’m not the fastest in the room anymore. Or I don’t just know the answer right away. It’s like I actually have to do some thinking. And for me, I think that problem solving process in our classrooms, like there is so much benefit from doing that work. And I look back to my own teaching and my own classroom. I had calculators out all the time in secondary math, and then I would still complain that kids had no number sense.

Kyle Pearce: Well, at the same time, while saying that, I had no idea that I actually didn’t have any number sense like you had cited earlier. So I know you’ve been talking recently all about the development of mathematical reasoning recently. We can’t go too, too deep into it. I know we’re going to be running out of time soon, but I do want to give you an opportunity just to kind of share why that is something that is so close to your heart. And I’m going to give a little bit of this cat out of the bag here because we, John and I, focus so much on this very same idea of mathematical reasoning.

Kyle Pearce: So I’m wondering, do you mind sharing like what is this development of mathematical reasoning and maybe where could they learn a little bit more about it if they want to dive deeper?

Pam Harris: You bet. You can learn about almost everything we’re talking about tonight more on my blog at mathisfigureoutable.com. And I have several blogs on the development of mathematical reasoning with some videos on my YouTube channel.

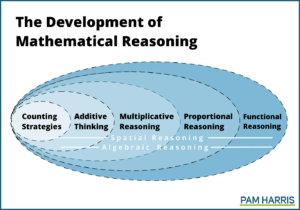
Pam Harris: But in brief, it is a graphic that I created to talk about how counting strategies lead to additive reasoning, and that leads to multiplicative reasoning. And all of these are embedded within each other. Multiplicative reasoning leads to proportional reasoning, which is embedded within functional reasoning, which I don’t love that name.

Pam Harris: I wish it was more about… because it’s not just functions, it’s also relations, but it’s that big idea of how we can really think and reason about functions and relations in high school math. And one of the main purposes for having this sort of nested set of kind of domains is to help teachers understand that whatever their imperative is, let’s say that I’m a third grade teacher. I would suggest that their job is to really help students develop additive reasoning into multiplicative reasoning.

Pam Harris: If that’s that particular teacher’s place to be, than what we don’t want to do is let them get answers to addition problems using the less sophisticated counting strategies or get answers to the multiplication problems using the less sophisticated additive reasoning. So, for example, proportional reasoning is more sophisticated than multiplicative reasoning. So when we as middle school teachers are supposed to be teaching students to be reasoning proportionally, what we don’t want to do is let them solve proportions using only multiplicative reasoning. We need to actually be helping them develop their brains to be reasoning proportionally. So all too many middle school teachers are, and to make textbooks and curriculum and the whole thing, teach students to solve proportions using cross multiply and divide.

Pam Harris: Well, if you think about cross multiply and divide, that’s multiplicative reasoning at best, if they’re even reasoning when they’re doing algorithms to cross multiply and divide. And that’s the reasoning from the level before. So I’m getting answers to a particular kind of problem, but I’m using reasoning before that. That can’t happen.

Pam Harris: We need to have teachers realize, ooh, if this is the kind of reasoning I’m supposed to be developing in students, then I want to actually develop that reasoning, not allow them to get answers using less sophisticated reasoning. So that’s kind of the big upshot of the development graphic is to help teachers realize what the different sophisticated levels are and that we need to be building that level of reasoning.

Kyle Pearce: Interesting. And you know, John and I both have taught many of the same courses. And one course in particular, anyone from Ontario who has taught a grade nine applied or a grade nine academic course. Oftentimes, I think what you’re saying, just for someone who’s been in the classroom, and I’m hearing, and I’m picturing the scenario of a student in my class that is even using additive thinking sometimes to solve proportional problems. So for example, a student building out a table and not even really respecting the fact that that’s actually this ratio table that we’re working with, and we’re actually just like adding up and down, which is an effective strategy at times, right?

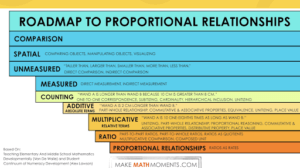
Kyle Pearce: It might be a very efficient strategy depending on what the question is asking. But if that’s where that student is always, and we’re not sort of like giving a little bit of that nudge to that multiplicative reasoning, helping them to see some of those connections through their own thinking, like listening to their work and helping to nudge that forward through our consolidations in our lesson, it is so important. And for John and I, we actually have what we call a roadmap to proportional relationships that myself and some other colleagues, including Eva Lehman, have spent a lot of time working around. And really they coincide so nicely. And I know for you, you actually have an online course built around proportional relationships and proportional reasoning.

Kyle Pearce: John and I both have one as well inside of our academy, and honestly, I look at both and I see such value in both. So for those who are listening and are really wanting to dive in, definitely check out both. I love Pam, how yours is all nested. Mine is sort of the way it’s lined up, it sort of looks like a bit of a continuum style. But all in all, they are attempting to do the same thing, which is helping people to move their own understanding a little further along as to what it is that we want students to be able to do with the mathematics and where we want them to get to with their own reasoning and their ability to problem solve.

Kyle Pearce: And essentially, to be able to notice a name where their students are, so they can help them along as well. So at this point, I’m looking at the time, Pam. We have had a blast. John, what else do we have to ask? Something really important for Pam here.

Jon Orr: Pam, if it’s okay with you, we would love to put that image of your graphic on the show notes page. Would that be okay?

Pam Harris: Yeah, absolutely.

Jon Orr: All right, so we’ll throw that on there. Plus all the other links that we’ve talked about and resources that we’ve talked about here on the show notes page. Pam, where can our listeners go say to learn more about you or get more learning from you? Where can they hit us up with some resources that we can also add to the show notes page that our listeners can learn more about you and learn more from you?

Pam Harris: Yeah, absolutely. And I love to connect, so I would love to see you on our Math Strat Chat. We launch Math Strat Chat every Wednesday evening. I throw out a question, people from all across the world throw in their strategies, explain their thinking. I try to interact as much as I can on Wednesday and Thursday. Honestly, I’ll leave it alone a little bit after that.

Pam Harris: We’re just starting a brand new part of Math Strat Chat, where we’re taking strategies that people put out on Twitter, Facebook, and Instagram, and we’re kind of compiling some of the top four or five strategies that we saw, and then we’re letting people vote on which one they liked the best.

Pam Harris: The vote is less important, but the cool part is that what we’re doing is naming strategies and words, kind of putting them in categories so people are then better able to kind of go, oh, okay. This strategy is different than that strategy. Even though they were both on a ratio table. I see how they were using different relationships. So we’re kind of helping people categorize, like getting better at those major, sophisticated strategies for each operation. So we’d love to see on Math Strat Chat. You don’t have to join us Wednesday nights. You really can look kind of any time, either Facebook, Instagram, or Twitter for that.

Pam Harris: And then mathisfigureoutable.com, if you can sign up for my weekly newsletter, my emails are actually planned out. They’re teaching emails. In a lot of the emails I actually teach something about the development of mathematical reasoning or models versus strategies or all sorts of things. So if you’re interested to connect with me that way, you can find that on the homepage at mathisfigureoutable.com.

Pam Harris: Like you guys said, I’m also developing online workshops. The first one is on developing proportional reasoning, but I’ve got several plan that will be coming out soon. And last but not least, we also have material for professional learning communities. If you meet in PLCs and you’d be interested to have really good material for you to study in your PLCs, then check out the product that we’ll be launching this fall, fall of 2020 all about material for PLCs.

Pam Harris: And there’s a few books out there too, if you’re interested. You can find them on my website.

Kyle Pearce: Fantastic. Pam, it has been a pleasure. I can’t believe how fast the time has flown. We actually had more questions for you, which means I think you’re going to have to make a repeat appearance on the podcast, if that’s okay with you.

Pam Harris: I would be honored.

Jon Orr: Awesome stuff.

Kyle Pearce: Thanks so much, Pam. We hope you have a fantastic evening and we will catch up with you either online, on Twitter, or in person at an upcoming conference.

Pam Harris: Great. Thanks guys.

Jon Orr: Take care.

Kyle Pearce: We want to thank Pam again for spending some time with us on the math moment maker community while she shared so many insights with us and you at home on our making math moments that matter podcast.

Jon Orr: As always, how will you reflect on what you’ve heard and learned from this episode. Because we all talk about some big ideas, but have you written anything down? Did you send out a tweet? Have you called a colleague to talk about this particular episode? Have you shared your learning at a PLC group? Be sure to engage in some form of reflection to ensure that the learning you did here sticks with you.

Kyle Pearce: And before you leave, we know you’re clearly interested in getting kids leaning in during your math lessons with the goal of building conceptual understanding, number fluency, and flexibility.

Jon Orr: How do we know? Well, you’re listening to a math podcast, of course. Want to take a deep dive into the make math moments three part framework? Download the three part framework guidebook by visiting makemathmoments.com/framework.

Kyle Pearce: In this downloadable ebook, you’ll be able to take the learning with you as you build your own understanding of how you can spark curiosity, fuel sense-making, and ignite your teacher moves in all of your math lessons.

Jon Orr: Go ahead and grab it now by visiting makemathmoments.com/framework. That’s makemathmoments.com/framework.

Kyle Pearce: In order to ensure you don’t miss out on new episodes as they come out each week, be sure to subscribe on iTunes or on your favorite podcasting platform.

Jon Orr: Also, if you’re liking what you’re hearing, please share the podcast with a colleague and help us reach a wider audience by leaving us a review on Apple podcasts and tweet us your biggest takeaway and tag us @makemathmoments on Twitter or Instagram.

Kyle Pearce: Show notes and links to resources from this episode can be found at makemathmoments.com/episode71. That’s makemathmoments.com/episode71.

Kyle Pearce: Well, math moment makers. Until next time, I’m Kyle Pearce.

Jon Orr: And I’m John Orr.

Kyle Pearce: High fives for us.

Jon Orr: And high fives for you.