Episode #363: My War Against Algebra Tricks – A Math Mentoring Moment
LISTEN NOW HERE…
WATCH NOW…
Have you been relying on endless algebra flowcharts to nowhere?
Are your students relying on tricks and shortcuts instead of truly understanding math? Are they seeing math as a set of disconnected procedures to apply and success comes when you figure out which procedure applies given a set of inputs?
Whether you teach elementary or high school, the tension between teaching for deep understanding and preparing students to “just get the answer” is real. In this episode, veteran math educator Maryann Greenholt shares her candid journey of grappling with how to move beyond procedural teaching—especially in the context of factoring—and what it really takes to help students understand the why behind the math.
You’ll learn:
- Why students at all levels often cling to memorized steps—and how to shift that mindset
- How using visual and concrete models can deepen understanding, from basic operations to polynomials
- What it looks like to create a calm, concept-first math classroom that builds confidence and curiosity
If you’re ready to move beyond surface-level math instruction and foster real meaning for your students, press play now and walk away with insights you can use at any grade.
Attention District Math Leaders:
How To Teach Algebra: A Course on Conceptual Understanding
Not sure what matters most when designing math improvement plans? Take this assessment and get a free customized report: https://makemathmoments.com/grow/
Ready to design your math improvement plan with guidance, support and using structure? Learn how to follow our 4 stage process. https://growyourmathprogram.com
Looking to supplement your curriculum with problem based lessons and units? Make Math Moments Problem Based Lessons & Units
Be Our Next Podcast Guest!
Join as an Interview Guest or on a Mentoring Moment Call

Apply to be a Featured Interview Guest
Book a Mentoring Moment Coaching Call
Are You an Official Math Moment Maker?

FULL TRANSCRIPT
Jon Orr: Hey there, Marianne. Thanks for joining us here on the Make Math Moments That Matter podcast. We’re excited to kind of dig in to a pebble rattling around in your shoe. But before we do, let us know. Where are you coming from? What’s your role? What’s going on in math in your world?
Maryann Greenholt: a high school math teacher. I currently teach Algebra 2 and only Algebra 2 and I teach at a technical school. the name is York County School of Technology, but we are a comprehensive technical school where students actively choose to leave their home school district. And since they’re high school, so they come here in ninth grade, they have all of their academics plus their technical area and they graduate. So it’s a really special place. We take students from 14 different school districts. all over York County. That’s where we’re located. I’ve been here for my entire career, which has been great.
Jon Orr: Awesome, awesome. When you say technical school, us a snapshot, because I know that some people are thinking, you know, I think they got a clear image, and some people are like, hmm, I wonder what that looks like.
Maryann Greenholt: All right, so we have a lot of different type of areas. I’m not going to try to give a number because it does change. But we have everything from what you might expect from old school technical schools like cosmetology, culinary, nursing, dental. We also have advanced engineering and manufacturing. We have students in mechatronics programs. We have students working on diesel trucks.
We have just so many different shop areas. Most students graduate with some type of certification in their shop area. Some will leave our high school and go right into industry making lots more money than I do. And some will go on to college and get a four-year degree and just use their technical area on the side. Or they’ll pursue a degree to get a job in that technical area.
Jon Orr: Awesome. Awesome. All right, that I think that gives us a good snapshot gives me anyone anyway, a good a good snapshot. Um, you know, the question I think we all we ask every guest on the making math moments that matter podcast is about their math moment. So when I say, you know, a memorable math moment, something pops into your mind, I’m sure, from your history from you as a student, or something when you were young, it stuck sticks with you, like you get this image of what of what math or math class looks like. And it kind of sticks with you all these years. Like, would you be able to describe what is a math moment for you?
Maryann Greenholt: So I’m gonna try, I don’t know if this is a conventional answer.
Jon Orr: No worries.
Maryann Greenholt: But math class for me, I’ve always enjoyed school certainly, because I’m still here. But I always found math class to be a calming place. It’s a place where you don’t have to constantly look at and reevaluate your work because you can check your answer, right? You know it’s correct. You know you can move on. And the first time in my life where math really showed me that was a calming type of practice was when my family was visiting an amusement park, probably Disney World. I was young.
And there’s four of us, right? We’re all standing in line to get on some type of ride with a gondola, right? That hangs on a wire. And very long line, we’re waiting there and there’s a sign that says the maximum weight that a gondola can hold is 700 pounds, right? And, you know, my brother, he’s older, he says, my parents is like, this is gonna be okay? Like, you know, are we okay here? And I looked at the sign, I looked at my family, I thought, okay.
Let’s say we each weigh 100 pounds, right? That’s 400 pounds. And then if I take all the extra weight that we all weigh over that, that extra weight has to equal 300 pounds. And there’s no way it equals that much. So we’re for sure not going to die. Like, we are fine, right? Yeah. So it was just a moment where I thought, I’m going to be fine because the numbers are working out here. And it was really just the first moment where I thought, wow, math is just this powerful thing, but
Jon Orr: We’re not falling off.
Maryann Greenholt: It’s a safety net, right? I was no longer panicked because the numbers were working in our favor.
Jon Orr: Right. Yeah. Amazing. Yeah. Like I, I don’t have a lot of the moments like that. Like I remember not, you know, I remember thinking that for me, cause my math moment was, you know, was about, and I shared that probably a few times over the years, you know, like it was a math moment about like just, I think just, just number crunching multiplication questions in the fifth grade, you know, just, just crunching these things and getting stickers and just feeling like the a million bucks because of, of this, just, just
memorization that I was doing, but I’ve never, I always saw that was what math was instead of the reality, like the realness of like where math lives in the world. I envy you for having that being your math moment. How does that transfer? Like how does that transfer into your role? Like obviously being at a technical school, it’s obviously helpful to think of it that way. And I’m sure it has provided you. great insight into the way that you’re teaching, how has it transferred into the way you teach math now?
Maryann Greenholt: So I always try to, number one, I do try to keep the classroom relatively calm environment. Students sometimes get panicked when there’s math involved. Just walking into a math class can give them anxiety. So I try my best to really remind them that it is just math, it’s just numbers, and we’re just working with them. It’s not as high stakes right now as it feels. So I try to…
give them that calming feeling that I get when I work on math. But also, I, so a few years ago, I can’t remember, I’m sorry, I’m with dates, during the summit, the online summit that you guys had, yes, there was a speaker and my husband and I, listened to it after our kids went to bed, so it was late at night.
Jon Orr: the Make Math Moments Virtual Summit, two years ago.
Maryann Greenholt: But we listened to a speaker and she said how there are kind of three reasons why people gravitate towards math. There are three types of math learners, right? There’s a type that they’re looking for connections at all times. There’s people that are desperately seeking an algorithm. And then, and those were the first two she said, I thought, I’m not either of those. And then she said, there are people that want to know why and they need to know why things work. And I thought, that’s me. That’s me.
And that is what I’ve always been seeking, is why things work, or more importantly with the gondola, why they’re gonna work out in my favor. So I really focus on that when I’m teaching. I want my students to conceptually understand why things work and not just jump straight to the algorithm.
Jon Orr: So it was safe to assume that like when you were in school, you were pushing on the why, and you probably weren’t blindly accepting, know, just know this algorithm and move on. Like were you desperately kind of going, I need to know why. was it frustrating to not know why? Because I’m sure like we all go through experiences where we have teachers where we didn’t know the why. was just like, we’re going to know that, you know, we’re going to do it this way versus that way. Did that frustrate you? Tell me about like, what that looked like a long time ago.
Maryann Greenholt: So there are certainly times, I will say, I am extremely blessed. I say all the time, I’m the product of amazing math teachers. I got all the good straws. Yeah, I got all the good straws on that. The exception to that was my freshman year of high school, I had geometry and.
Jon Orr: Hey, there’s hope then, there’s hope.
Maryann Greenholt: We have block scheduling, so we only had math class for one semester. And my math teacher, who is amazing, heard great things about her. My brother had her. She was out the entire time with pneumonia. And all they could find for us was a long-term chemistry substitute. So she certainly tried her best, but she wasn’t necessarily able to provide that y factor in there. And she really did provide us with algorithms as much as she could.
But there was one time we were just simplifying ratios. And I just remember thinking like, this cannot possibly be how this works. There’s got to be a better reason with this. was similar triangles. And that was a time where I just remember thinking that this has got to be easier than what I’m seeing. And if I could just understand why this works, it would be better.
Jon Orr: Right. Got it. Got it. Marianne, what’s the pebble, you know, around in your shoe right now? You know, like we, let’s unpack something for you. So you kind of take away and go, hey, I’m teaching algebra. Something’s rattling around right now that I wish I could pluck out. Talk to us about it.
Maryann Greenholt: All right. So my huge pebble has been a pebble for a long time is factoring. Yep. And when you guys were a couple of weeks ago, you had the podcast about tricks we use, right?
when really we should teach students why they’re working. So obviously love that one for that reason. And even though you said at the beginning of episode, this is a lot of elementary school stuff, in the back of my head I’m thinking, please do factoring, please do factoring, please do factoring. Because to me, and I’m hot off of factoring right now, we’re solving quadratics. To me, factoring is kind of two situations, right? Students are either at the mercy of remembering
an elaborate system of tricks, or they are at the mercy of having the right type of calculator that will factor for them, right? And I just thought, I’ve had a hard time of factoring for years. And again, I’m the product of great math teachers, but I will say the math background that I had in high school did not focus on factoring. We learned that it is a step that you do.
They certainly at some point taught us probably all of these ways to factor. But then at the end of the day, it was a step in a process and a problem we were solving. And we were allowed to use our calculator, which would factor for us. So that’s kind of my own background of factoring. I went to college, right? And everything was fine, truly. I have lived most of my life with no real deep understanding of factoring.
And it’s been fine. Now, as I teach all of those different strategies, your cubes, your difference of squares, I’ve gotten good, I think, at explaining to my students why each individual strategy works. I can show them why difference of squares works out. I can show them other ways to solve those. I can explain why the cubes work out. I can explain to them why each individual one works out. But at the end of the day, when they’re faced with a factoring problem, they have to go through
this elaborate flowchart, which I help them learn of, okay, first try this, then try that, and then, ooh, you got a decimal, that doesn’t really factor, and then maybe try this. It just seems unfair. It seems unfair that the students are at the mercy again of memorizing all these different strategies that may or may not work, or having the right type of calculator. And the best analogy I can give it is, and I don’t know, because I don’t teach elementary school, but,
If we stood in front of elementary school students and said, we’re going to divide numbers, and if all you ever told them was, well, if it’s even, we divide by 2. And if the digits add to something that’s divisible by 3, can divide the whole number by 3. If it ends at a 0, you can divide by 10, but also 5. If all we ever did was tell them those, but never said to them, OK, look, you can’t remember all those strategies, those nice shortcuts, well, guess what? There’s this algorithm.
that works for any number you could ever want to divide. And we’re going to show you how that works. As far as I know, the factory doesn’t have that. There’s no algorithm, there’s no concept, there’s no strategy that works no matter what type of polynomial you have. So that is the trouble that I’m having. And I’m sorry I’m long-winded about this.
Obviously, it’s something I’ve struggled with my students for a long time because I don’t want them to be at the mercy of thinking of two numbers that multiply something and add to something else, right, when there’s a bigger, better problem going on.
Jon Orr: at it. Now first, I have to say like, you feel like you’ve significantly dated me by by saying that you had a calculator that used to factor for you. and those that exist when I was in school and didn’t exist when I was teaching so are like like they they were there in the end, you know, like those last or guess I guess when I started teaching there was you could get your hands on
Let me ask you this. what you’re saying is that you want to help your students with obviously the skill of factoring and also understanding probably why when we factor or why we factor when we factor. I think going back to your moment is understanding the why is essential for you and you want to pass it on to your students. And it sounds like you’re not sure the why yet.
of like, do these work? Like, why is probably like, I think you get why we factor like that makes sense to you. Like, I don’t I’m not I’m not worried about that part. But I think it’s like, where is what’s happening, say, algorithmically here, that we need to unpack so that my students can like, see this as not three different sets of tricks, but one, you know, and I’m gonna I’m gonna ask you to reflect somewhere else that’s not on factoring. So so
what’s a situation where you feel like you’ve done a really great job of helping kids understand the why behind something and then maybe how they can be fluid with that idea versus, there’s a whole bunch of different scenarios and cases here that we now just have to show you the different scenarios and cases and you’ve got to memorize them.
Maryann Greenholt: Boy! we’ve been factoring now for a month in this classroom. And now we’re solving quadratics also by factoring. I have been in factoring land for a long time.
So I think this year I really help my students understand why special right triangles work out really well. Another area I think is powers of eye. So I did a really great job. I’ll go with that one because I think it’s a little bit easier here. I did a really great job this year I think, hopefully, of explaining to my students
why when you reduce any power of i, you’re only going to get one of four options. And I had them really develop that pattern and understand with the exponent rules how everything’s connected there. And they themselves then figured out essentially the shortcut of divide by four and looking at the remainder. And not only did they figure out the shortcut on their own, they understood why that worked and why all we cared about was the remainder.
So I felt very successful in that they understood that concept enough to come up with a shortcut and then use it. So I would go with that one. I would go with the powers of I.
Jon Orr: Got it. Got it. So you created a scenario, you created a situation and an activity for students to kind of grapple and dabble. And through the grappling and the dabbling, they found some patterns. And from those patterns, they built their own, in a way, their own algorithm to solve problems and rules moving forward. Does that sound true? Gotcha.
Yes, and I have had them do similar things with individual factoring strategies. Certainly, difference of squares is an easy one for that. Yeah, but I haven’t been able to generalize that to any polynomial.
Got it. Got it. Now, is it safe to say that all of those, that activity or that sequence of problems or the struggle or the dabbling that you were getting students to do, was this all in, were the representations you were getting students to utilize all in the abstract land, which means that we’re using symbols, numbers in this way to find the pattern or was there any sort of pictures being drawn?
representations that are not say abstract, even though sometimes pictures are abstract, but they’re more representational. So I’m talking about kind of the CRA model, the concrete representational abstract. Sometimes, you know, especially in high school, we tend to put emphasis on the abstract, which is our, our, our, our symbols and our ways we write equations, whereas, you know, most and if not, someone could argue all math could be represented in
representational, so maybe a picture or diagram, but then also concrete. So when you think about that activity that you had success on, was that just representation, or was that just say the abstract land and we’re just playing with patterns, or was there any sort of example, any sort of relation back to the concrete? And if, if not, is there any other kind of scenario out there where you dabbled or had students dabble in the concrete or the representational and not just the abstract?
Maryann Greenholt: So with powers of I, it was all abstract. It was not concrete. It is. But I have, so for the first seven years of my career here at Tech, I exclusively co-taught classes. So I started out co-teaching pre-algebra, which we don’t even offer anymore because it’s not a high school credit.
Jon Orr: Right. I is very abstract idea.
Maryann Greenholt: And I could talk remedial algebra, I could talk geometry. I could talk a lot. So I’ve used a lot of concrete models throughout the years. Some were successful than others. love, I don’t know if any of the listeners out there do this, but I love solving equations with cups and then elbow macaroni. You know, to show the value of that, love that. And I have used my share of algebra tiles. So with factoring,
When I taught factoring, when I had, we call it algebra AB, is our remedial level of algebra, or regular algebra one. I’ve done that as well. I’ve used algebra tiles to show them how to factor. And certainly it does help them truly understand that you’re finding the area, right? You’re using an area model with length and width. And then I don’t know if this jargon is gonna work for anyone, but.
then the area model with the algebra tiles translates very nicely to a strategy that we call the Xbox, which is really just factor, I’m talking about trinomials here, but it’s really just factor by grouping, but with a scaffold. Yeah, so I’ve done the algebra tiles in that respect, but not necessarily with algebra two with anything other than your GCF, your trinomials or your difference of squares.
Jon Orr: It sounds like you tried it, but you went away from it. It didn’t become a consistent component of, of like, let’s say the tools in your, in your teaching arsenal. Is that true? What’s the, what would you say is the, the, know, the reason they’re like, what, what, what about algebra tiles? Cause there’s lots of thoughts and opinions and, you know, debates around the use of algebra tiles, but what’s, what was, what would be your say? Hey, I don’t use those anymore because.
Maryann Greenholt: Mm-hmm. I’d agree with that, yeah. Truthfully, just when I switched to Algebra 2, I didn’t use them anymore. With Algebra 2, my students, which this is wonderful, they have an incoming knowledge of how to factor those items I just went over with you. So they have retained that knowledge. They did it in Algebra 1. They have done it again in geometry, which we have before Algebra 2. So they have that incoming knowledge.
The ones that we’re grappling with in algebra 2 that are new to them are your difference of cubes, your sum of cubes, and then four-term polynomials, which for them end up being easy because it’s a lot of just grouping again. And I’ll be 100 % honest, I don’t know how to use algebra tiles to do a sum or difference of cubes. I’ve never looked at it. I have used algebra tiles for completing the square. Yeah.
Jon Orr: Right. Right. You need cubes. That’s why.
Maryann Greenholt: But yeah, I’ve never used algebra tiles for the cubic.
Jon Orr: Right, yeah, yeah. Well, yeah, that’s the reason, right? Like you need cubes to be able to actually concretely manipulate what that looks like, or connect cubes. And connect cubes can work really well when you’re kind of dabbling in that area. But when you think about, say, those students, like what I heard you just say is like kids come in already having this baseline understanding.
Would you say they have a strong conceptual understanding of it or they just have that surface level? I know how to do this when I recognize the polynomial looks like this and therefore I can regurgitate the, two numbers that multiply to this, add to this, I got it. Or I can use decomposition to factor this because I learned it in algebra one. Is that the level or do you feel like your students could demonstrate, say, different representations of that and have a more deeper understanding of
representing that differently because in my experience, you know, and I did this too, is when I taught advanced functions here in Ontario, which is like your pre-calculus, we do, ours is, our courses are all kind of chunked up differently than your courses. So we do a lot of say what you just said about factoring, say higher level polynomials. So of degree three or higher.
in that class, but whereas we don’t do that in say our 11th grade as much, we wait till our 12th grade, because our 11th grade is still like, all ideas kind of jump together still like a ninth grade, ninth and 10th. So when I think about that though, is what I used to also assume that they had what they need to be able to do what I want them to do, which, but I still was treating say,
factoring at that level as what their extension of what they had learned in the past is like, they know this type of factoring. Therefore, the way they learned it was recognizing what type of polynomial I have. But basically, the mini version of your flow chart, you know, hey, this is the type of polynomial I have. A is not one, I do this. A is one, I do this. You know, then I do this. If A looks like this, or if there’s a common factor, the way I was still treating it that way, because I was relying on
that past understanding of what they were coming to me with, which was a very surface level of the algebraic representation of how to factor, which then was also based off, and you know this, being an Algebra 2 and Algebra 1 teacher, is that it’s based off of the representation, or the abstract representation of expanding. And if we could get them to expand and multiply, and using the distributive property over and over and over again, we can.
see some patterns if we reverse this, reverse it, and we start to kind of generalize that way. However, I started to make significant gains when I started to dabble with those representations that were not just the abstract, was, look, thinking of the area model and how that translates into other types of models. So trying to help our students see that
when we’re factoring, can draw area models to represent, you know, like I don’t use, don’t, I never, I never really got into algebra tiles as, as the way I think most people do because once we maxed out, know, Hey, I got these algebra tiles to actually like factor with or, or expand with, or use a distributor property with. but we ran out of tiles, you know, so we just started drawing, you know, drawing all of a sudden it became easier to draw an area model.
And an area model is a vertical model that stretches from the third grade all the way up to the 12th grade or pre-calculus because you can use that area model in lots of different ways to factor to a distributed property to, you know, there is no more rules if we say use this model because I don’t have to talk about foil. We don’t have to talk about, you know, the order of which to multiply. It’s where we’re multiplying a two-digit by two-digit number in the fourth, fifth grades. That’s the same as multiplying two binomials in
upper grades or in the ninth, 10th and 11th and 12th grades. And so when those students came in and I made that assumption, I had students in the 12th grade or 11th grade struggling to factor because they were trying to memorize this flow chart. And when I went backwards and I stopped making the assumption that they understood, like why are we factoring?
And I went back to multiplying numbers. And then we kind of in one period, this is what I used to do in my my pre-calculus class when I wanted to divide polynomials or factor polynomials with degree three or higher. We went back to learning in one one 75 minute period, we would cover why we multiply and how we multiply two digit by two digit numbers without calculator.
and without stacking numbers, like why, or we even actually go over why stacking numbers actually works and why we carry this and why we carry that. And we unpack the multiplying and then we represent it in a different way. That’s stacking. So all of a sudden we now talk about the area model. It’s like we could draw this diagram to show that we’re really finding the area of a rectangle when we multiply two digit by two digit numbers. And then that’s easily transferred into multiplying two binomials together.
And hey, we’ve got the length, we’ve got the width. know, one the pieces of the length is an unknown value, like an x, and then the other is like plus one, like plus one more. And then the width is maybe two x’s long, or two x, and then plus five. And then we find the area as a representation in an abstract way using that, and we do that again. And then what we do is we reverse it. And we say, well, what happens if we’re dividing? What does division look like? let’s divide a two-digit number by a one-digit number.
What are we doing with the standard algorithm when we do that? Like what is really happening there? How can we represent that on an area model? How can we represent division with an array? How can we represent that by drawing this picture? And what are we really doing when we’re like figuring out how many times this goes into this? maybe we all of sudden think about it in terms of repeated subtraction. There’s two different types of division. Sometimes it matters when we refer to one versus the other. So when we start unpacking the division,
from third grade, fourth grade. Because you think these kids know this, but they don’t, right? They don’t. need to be, they need that experience of seeing the beliefs they hold about certain mathematical ideas in a different way. And sometimes that way can help them see and see the algorithms that you’re trying to teach in a different way as well. So when we go through that history of…
division from third grade, fourth grade. What does it look like in seventh grade? All of a sudden algebra, why, why when we, like, what does it look like when we’re dividing polynomials? Like when we’re dividing this by this, really what we’re doing is we’re factoring. we already know if we’re dividing polynomials and we already know one of the factors, then we’re finding the other factor. When we divide this polynomial by this and all of a sudden we can start seeing the way that we can represent factoring.
in a different way than say just the area, you know, looking at this algorithmic way. Because I get, you you can go out on a limb and say that, you know, these, these, these algorithms that we’re showing kids about some of these things all are just different representations of filling in areas or filling in space, you know, cause you could represent any two digit by two digit, like any binomial by that binomial. So any quadratic, you know, that as a representation is a length times a width.
And you’re really just finding the area and the pieces of the areas and combining them together. And just the base that you’re working with is base X instead of base 10, like when you’re multiplying numbers. So when you worked with a polynomial of degree three, you’re finding, like I said, cubes is the actual concrete thing you would need. If you’re going to use algebra tiles, you’d have algebra cubes, which they do exist. can find them. They’re hard to find sometimes, but you can represent
that but really what you’re doing is you’re finding the amount in the space, right? You have length times width times height now of what you’re trying to find and now you’re still working in base X and we can then work through different patterns. But some of those techniques, like when we think about, I think you said earlier in the call was that
What are we doing to help our kids not see all these as separate techniques? But when you relate it back to one idea, students start to realize that it’s not separate techniques, because difference of squares and factoring by like factoring a trinomial where a is not one is the same process. just you have to treat it as the same process, which means like there aren’t you don’t have to show two different techniques to solve that problem. You can show one technique to solve the problem because we’re really just finding area.
of the space on the inside. So I have found success when I try to rewind and go backwards and try to go, what is really occurring here? What is the representation I actually have when I’m working with these three dimensions or with these two dimensions? And then helping our students see that that’s also the case. And all of sudden you have students, you’ll see students solving problems in different ways that you thought and factoring in different ways than you thought.
because either their trialing and airing is getting better or their algorithmic way of remembering is getting better because they can draw a picture. Or you’ll find, like I did, I had students factoring in their heads because they could visualize what was happening in, say, the three dimensions or the two dimensions. We had students completing the square in their head because we drew pictures of squares instead of, hey, find half the B and square it and then add this and subtract this.
So I guess my recommendation is take a deeper dive or take a dive into those representations and go, can I work with my students on that? if something that’s a barrier there for me right now is I don’t know how to do that, then that’s your next step is how do I unpack what it looks like, sounds like, and can I represent this without using the calculator that factors for me or using one of my algorithms? Can I represent this?
in different ways that can make sense to me. If it can make sense to me, then I can then make sense for the kids. And it doesn’t have to be like the one way here and the one way here and this ultimate flowchart. Okay, I said a lot. What’s your thoughts?
Maryann Greenholt: No, I think that’s a great suggestion, truly, because especially this year, it would have been great had I made this phone call a little earlier. Because my students this year, I noticed I do.
Jon Orr: Hahaha. Now you got a year to practice and dabble and you’ll get them next year.
Maryann Greenholt: Yeah, it’s helpful. It’s for sure to have that time in between. This year my students have, this is different for me than normal, but my students early in the year, whenever we would multiply any type of polynomials, they did automatically go towards the area model to multiply their polynomials rather than, I say errors is the other option because truthfully that acronym FOIL, it grates on my nerves like nothing else.
Jon Orr: Good. Got it. Yeah. Yeah, it’s the four letter word that starts with F.
Maryann Greenholt: I hate that one. that they would go to the area model. I noticed, yeah, I didn’t stop them, obviously. I said, this is great. Like, this is what the majority of you are doing. This is when we do problems on the board. I said, this what I’ll do. I said, I’m down for this. I said, certainly, if I’m multiplying a trinomial by a trinomial, yeah, I’m not going to have this big long line of stuff. I’m going to draw an area model. So I said, I’m here for this. So because my students this year already are gravitating towards that model with multiplying,
it would have been a very easy jump then, right, to represent the factoring that way as well. So I think this year it would have been effective. Now, I suspect, and I don’t know what I’ll teach next year. Here’s hoping I teach this again, but if I teach algebra two again next year, it’s something for me to keep in mind that my students aren’t showing that natural gravitating towards the area model with multiplying to kind of…
push it a little bit or suggest it a little bit more to front load it for the factoring to represent it that way. Now I’m wondering, and so my husband is a math specialist and he also was on your podcast a few years ago. So yes, he was. are husband and wife math to Kyle actually.
Jon Orr: What? What’s his first name? I was gonna say it’s a Kyle. Kyle first like, yeah, and putting two and two together. I recognized the last name and I was about to say Kyle. Hey, two for one, two for two, I think. There you go.
Maryann Greenholt: Yep, yep, that’s him. he, that’s right. We are all math all the time in our house. So he is currently a math specialist at a middle school. He also works with elementary school teachers on their curriculum. So he has lots of great resources for me in terms of those concrete representations, which is really helpful to have that build of support. But I’m gonna ask you the same thing. What, what,
websites can you direct me to that have kind of the virtual advertiles or possibly those virtual cubes, right, that are harder to come by physically where you can at least have it on a laptop. Our students, yay, are one-to-one in terms of technology and a lot of them coming through now have touch screens. So yeah, what websites can you recommend?
Jon Orr: There’s three, there’s three that come to mind pretty quickly. And I’ll tell you the three differences. I guess two are very similar. So one of the first virtual manipulative tools that I got my hands on a number of years ago was Braining Camp. Braining Camp, if you’ve been in some of our webinars lately, you would have.
You’d see Yvette Lehman, which is one of the coaches here at Make Math Moments, dive in with Braining Camp because she finds the middle of tools and the whiteboard very interactive. What I found, and I think she would agree, is that sometimes Braining Camp feels or has more tools towards elementary than high school. Where I say used more in the last, say, five years of my teaching career, I taught for 19 years before I became math coach, math coordinator, math consultant.
was, was Mathagon, which is now, which is now an amplify product. and Mathagon again, very similar to branding camp, digital, digital tools. they have, they have algebra tiles. I don’t believe that they’re going to have the cubes. but the third one would be say Desmos, math, which would have, and what you’re going to find there is, is if, if you can find some say custom made.
classroom activities that are specifically for factoring or for factoring of higher polynomials. You’ll have to do some digging though to find some of those. But you know, the user base there will have created some activities along the way that would maybe kind of give you some nuggets, but you’ll have to kind of do some searching, some digging to find some of those. I know it’s been harder lately after Desmos transition to Amplify to find some of the, you know, the
the user created activities because you used to be able to, or you still can create your own activities, but then they used to be able to be searchable. So it’s harder to find them now, but you should be able to find some activities that are say higher level polynomial division or polynomial factoring activities that kind of may not have the actual virtual medibul of tool there, but give you some activities that kind of like help you understand it as well. So those are three to kind of, would say check out. if you have say access to computers with students to be able to kind of manipulate with.
Maryann Greenholt: Yeah, that’d be great. We use Desmos now. yeah, that’ll certainly be a go-to. And then definitely the other two, certainly to have the students be able to be able to be themselves. About the…
Jon Orr: Yeah, check it out. Got it. What did Kyle say to you? You said you asked him that and what was his response? No, the tools, the tools to use, the websites.
Maryann Greenholt: Oh gosh, I’ll be honest, he shows me a lot of websites. Some of them I, well Desmos I use a lot now. And then some of the others, I believe he probably has showed me Mathagon. And then he also showed me, now this is not, it’s not a manipulative website. I hope I remember the name, Grass Bowl Math? Grass…
Jon Orr: Grass boat, yeah, it sounds familiar.
Maryann Greenholt: Graspable. But essentially, when you’re solving an equation, honestly is what a few times we’re doing the work on the computer is more work than just doing it by hand because you have to show like you’re dragging and dropping essentially and moving things around. But you cannot skip a step. Like if you want to divide or do anything with fractions, you’re doing every individual step. And then it falls through on the step that you ask it to do. which is real entertaining if you make a mistake, right? Because it’s gonna do it, it’s gonna do whatever you ask it to do and then you see the results of your actions is what you do.
Jon Orr: Right. Got it. Got it. Marianne, what would you say is your big takeaway from today’s chat?
Maryann Greenholt: think the big takeaway is really honing in on my students’ natural gravitating towards the area model, expanding on that. And also the idea that you showed your students the concrete representations from their previous knowledge up to what they’re covering currently in that 75 minutes, I find that really encouraging because I think every teacher’s in a situation where there is never enough time.
You always feel pressured. My students aren’t necessarily headed towards a state standardized test that they have to pass, but they are head to the SAT. I want them to have all that knowledge. So hearing that you’re able to do that in 75 minutes is huge. Yeah.
Jon Orr: It’ll save you time. To be honest, it’ll save you time in the long run to kind of rewind and then fast forward.
Maryann Greenholt: Yes, I think so. see that I’ve switched up how I do my openers the past couple years and kind of same idea. Yes, something that takes a few extra minutes in the day often will save you that time later.
Jon Orr: Sure. Perfect. Another place, specifically I talked about that progression, the lesson that I did with my students to rewind back to division, back to multiplication, and then fast forward into almost like a progression of division from third through fourth grade all the way up to the 12th grade with divisional polynomials. There is a video on YouTube.
If you go to our YouTube channel, there’s a playlist about how to teach algebra. And there are seven or eight videos there about the progression of factoring and how do you represent that this way and that way and factoring with fractions, know, factoring this way, you know. So I would check that out. You can see that progression video lesson that I do with my students when I do that rewinding. And that’s the order I do it. And that’s the examples I even use with those students. So.
We have one there for multiplying into the distributed property up to the higher levels and also one for division up to the factoring for polynomials. So check those out. Mary Ann, I want to thank you for joining me. And I know Kyle missed this. Your Kyle and my Kyle here too. They all missed this and they’ll be itching to get back on here soon. But hopefully we can check it with you.
next year and see how this factoring lesson went a year from now. there was any sort of differences along the way, you okay with that? Awesome, awesome. Thanks so much and good luck.
Maryann Greenholt: Yes, absolutely, I would love that. Thank you so much. a good day.
Jon Orr: Take care.
Thanks For Listening
- Book a Math Mentoring Moment
- Apply to be a Featured Interview Guest
- Leave a note in the comment section below.
- Share this show on Twitter, or Facebook.
To help out the show:
- Leave an honest review on iTunes. Your ratings and reviews really help and we read each one.
- Subscribe on iTunes, Google Play, and Spotify.
DOWNLOAD THE 3 ACT MATH TASK TIP SHEET SO THEY RUN WITHOUT A HITCH!
Download the 2-page printable 3 Act Math Tip Sheet to ensure that you have the best start to your journey using 3 Act math Tasks to spark curiosity and fuel sense making in your math classroom!
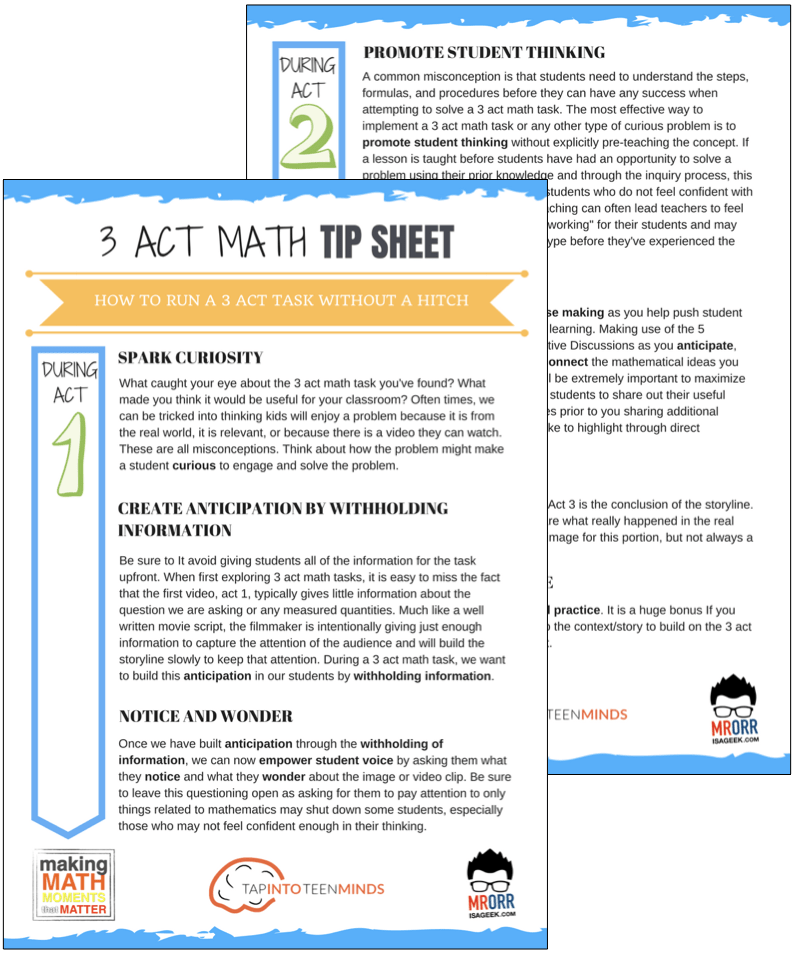
LESSONS TO MAKE MATH MOMENTS
Each lesson consists of:
Each Make Math Moments Problem Based Lesson consists of a Teacher Guide to lead you step-by-step through the planning process to ensure your lesson runs without a hitch!
Each Teacher Guide consists of:
- Intentionality of the lesson;
- A step-by-step walk through of each phase of the lesson;
- Visuals, animations, and videos unpacking big ideas, strategies, and models we intend to emerge during the lesson;
- Sample student approaches to assist in anticipating what your students might do;
- Resources and downloads including Keynote, Powerpoint, Media Files, and Teacher Guide printable PDF; and,
- Much more!
Each Make Math Moments Problem Based Lesson begins with a story, visual, video, or other method to Spark Curiosity through context.
Students will often Notice and Wonder before making an estimate to draw them in and invest in the problem.
After student voice has been heard and acknowledged, we will set students off on a Productive Struggle via a prompt related to the Spark context.
These prompts are given each lesson with the following conditions:
- No calculators are to be used; and,
- Students are to focus on how they can convince their math community that their solution is valid.
Students are left to engage in a productive struggle as the facilitator circulates to observe and engage in conversation as a means of assessing formatively.
The facilitator is instructed through the Teacher Guide on what specific strategies and models could be used to make connections and consolidate the learning from the lesson.
Often times, animations and walk through videos are provided in the Teacher Guide to assist with planning and delivering the consolidation.
A review image, video, or animation is provided as a conclusion to the task from the lesson.
While this might feel like a natural ending to the context students have been exploring, it is just the beginning as we look to leverage this context via extensions and additional lessons to dig deeper.
At the end of each lesson, consolidation prompts and/or extensions are crafted for students to purposefully practice and demonstrate their current understanding.
Facilitators are encouraged to collect these consolidation prompts as a means to engage in the assessment process and inform next moves for instruction.
In multi-day units of study, Math Talks are crafted to help build on the thinking from the previous day and build towards the next step in the developmental progression of the concept(s) we are exploring.
Each Math Talk is constructed as a string of related problems that build with intentionality to emerge specific big ideas, strategies, and mathematical models.
Make Math Moments Problem Based Lessons and Day 1 Teacher Guides are openly available for you to leverage and use with your students without becoming a Make Math Moments Academy Member.
Use our OPEN ACCESS multi-day problem based units!
Make Math Moments Problem Based Lessons and Day 1 Teacher Guides are openly available for you to leverage and use with your students without becoming a Make Math Moments Academy Member.
Partitive Division Resulting in a Fraction
Equivalence and Algebraic Substitution
Represent Categorical Data & Explore Mean
Downloadable resources including blackline masters, handouts, printable Tips Sheets, slide shows, and media files do require a Make Math Moments Academy Membership.
ONLINE WORKSHOP REGISTRATION

Pedagogically aligned for teachers of K through Grade 12 with content specific examples from Grades 3 through Grade 10.
In our self-paced, 12-week Online Workshop, you'll learn how to craft new and transform your current lessons to Spark Curiosity, Fuel Sense Making, and Ignite Your Teacher Moves to promote resilient problem solvers.










0 Comments