Episode #21: The Thinking Classroom: An interview with Peter Liljedahl
LISTEN NOW…
In this Math Moment Interview, we talk with Dr. Peter Liljedahl, Professor of mathematics education at Simon Fraser University who has been researching ways to get students to become resilient problem solvers through ideas such as using vertical non-permanent surfaces, visible random groupings, selecting tasks with evolving complexity, and much more…He calls his work The Thinking Classroom.
You’ll Learn
- The elements needed to build a thinking classroom.
- How to build a problem-solving culture in your classroom.
- Why we need to think critically about the choices we make about our environments and lessons.
- Why vertical non-permanent surfaces will change your students engagement in math class.
- How to make effective groups in math class.
Resources
Peter’s Website: http://www.peterliljedahl.com/
Building Thinking Classrooms on Edutopia https://www.edutopia.org/article/building-thinking-classroom-math
The Unit Circle that Peter references:
The Thinking Classroom:
FULL TRANSCRIPT
Download a PDF version | Listen, read, export in our reader
CLICK HERE TO VIEW TRANSCRIPT
Peter Liljedahl: My goal and thinking classrooms has always been not to build and find engaging tasks, but to build, engage students that can then be pointed and then you point those engaged students [crosstalk 00:00:15].
Jon Orr: You’re listening to an interview with an influencer who has made a big impact on how we lead our lessons, and more importantly, how we structure our math classrooms. That’s right. Today. we’ll be spending some time with the man building thinking classrooms all over the world, Dr. Peter Liljedahl.
Kyle Pearce: In this math moment interview, we begin with Peter’s story that led him down the road to teaching secondary mathematics before shifting his focus to work with pre-service math teachers at Simon Fraser University in British Columbia, and engaging in research that is getting students standing and thinking in their math classes. This is episode number 21, The Thinking Classroom. An interview with Dr. Peter Liljedahl. Get ready to stand up. Join your visible random grouping and head over to the vertical non-permanent surface. It’s time to do some thinking. Start the intro music.
Kyle Pearce: Welcome to the Making Math Moments That Matter podcast. I’m Kyle Pierce.
Jon Orr: And I’m Jon or we are two math teachers who together …
Kyle Pearce: With you the community of educators worldwide who want to build and deliver math lessons that spark engagement …
Jon Orr: Fuel learning …
Kyle Pearce: … and ignite teacher action. Well, I know I’m ready to go. How about you Jon?
Jon Orr: For sure. We want to welcome Dr. Peter Liljedahl, professor of mathematics education at Simon Fraser University, who has been researching ways to get students to become resilient problem solvers through ideas such as using vertical non-permanent services, visible random groupings, selecting tasks with evolving complexity and much more. Well, it’s now the time to put that phone in your pocket and listened to Peter give us some great insights.
Jon Orr: Hey there, Peter. How are you doing on this stormy day while here in Ontario? Anyway, how are you doing today?
Peter Liljedahl: I’m doing great. I just got back from South Africa yesterday, so today has been more of a home day, taking care of business around the house and catching up on email.
Jon Orr: South Africa. As we were just talking about before the recording started, but how hot was it there? They’re in their opposite season right now.
Peter Liljedahl: Yeah, 35 degrees.
Jon Orr: Jeez.
Peter Liljedahl: Yeah. A few days before I went I was in Saskatoon where it was minus 31 so I think that’s a record for me for temperature swings across a short span of time.
Kyle Pearce: Well, that sounds like a pretty interesting math lesson around integers. You could have some fun there for sure. Well, why don’t we take a couple of minutes here. Do you mind introducing yourself? I know many in the math community are aware of who you are, but what’s your role in math education and what sort of makes you tick when it comes to a math education and really trying to push thinking further in the math education space?
Peter Liljedahl: Well, I’m a professor at Simon Fraser University. I’m in the faculty of education and my unofficial title is professor of mathematics education. I would say that I’ve specialized in teaching and learning, meaning that most of my research and most of my own personal interests and curiosities lie within the ideas of teaching as informed by trying to motivate better learning in students, and I’m a former high school math teachers, so my roots are in the classroom and I think that has greatly informed my interests.
Kyle Pearce: Oh, I can only imagine.
Jon Orr: That sparks my interest right now, that journey from high school math teacher to professor or professor back to high school. Can you maybe fill us in on your say math journey even thinking back to when you were young, what did that path look like for you?
Peter Liljedahl: Okay, so people may have noticed that my last name is not a typical Canadian last name. I was born in Sweden and we immigrated to Canada when I was eight years old. When we did that, the only thing that I could really take with me was mathematics. I was pretty good at math in Sweden, but when I move to Canada and integrate three, that was really the only place I could gain any footing. So I put a lot of energy there. So, math became something, and this idea of math as a universal language, I guess is true in this regard. Math was always something that I was good at, I was interested in, I excelled at, I sometimes accelerated at. Went through high school, did very well in high school and off to university.
Peter Liljedahl: It’s interesting, I just gave a talk to a group of students in high school the week before I went to South Africa and I was saying that when I graduated high school, my plan was simple. My plan was simple. I was going to go to UBC, University of British Columbia, I was going to get a degree in mathematics and I was going to become a mathematician, whatever that meant. I had no clue what that meant.
Jon Orr: I still don’t.
Peter Liljedahl: I think this is one of the things that grade 12 students are often faced with, when math is what they’re good at. What are you going to do with that? Partway through my math degree, and I took a long time to get my undergraduate degree. I was dabbling in sport at the time as well, but at some point I realized that, okay so math is … I think I realized I wasn’t going to become a mathematician. I was getting a better idea of what that was, but I realized that math was my toolkit, but I had yet a topic to apply it to.
Peter Liljedahl: So, I started shifting into courses in computing science. I picked up a minor in computing science thinking that that would be the direction I would go in because that was a nice place to apply mathematics. I realized that I liked programming a little bit too much, like obsessively too much. I was thinking that that was not a healthy lifestyle choice.
Kyle Pearce: Were you actually coding or just playing the games? Because I’ll take one a little more than the other, right?
Peter Liljedahl: I was being a little bit of a perfectionist with it. Even when I had the code working exactly the way I wanted, I wanted it to be more compact and more efficient than … back then, memory was expensive and so on. So, it was about trying to make efficiencies, which appealed to my, I guess the aesthetics of mathematics. There had been a number of circumstances by which I had had some encounters with teaching mathematics during this time. One of which was I’d been walking through the concourse at SFU. I had switched to SFU, by the way. So I finished my undergraduate degree at Simon Fraser University, where I’m now a professor, but I was walking through the concourse and they had this, one of the bulletin boards is like, come, be a TA in mathematics and calculus and it had the little strips of paper that you could tear off.
Peter Liljedahl: So I pulled that off. I made a call, I got an appointment. There was to be a TA at the university in the math department. I remember I showed up for the meeting and the person interviewing me was a woman by the name of [Tosula 00:07:00] Bergen, who is now the consular general for Cyprus in Canada, but she’s a Cypriot and she was a mathematician and her husband was a mathematician in the math department. I remember I showed up for the meeting. She says, “Tell me a few things about yourself.” And I did. And she says, “We don’t normally hire undergraduates. This ad was for graduate students.” And I said, “Oh well, okay, well thank you for your time.” And she goes, “No, no, no. Tell me a little bit more about yourself.” One of the things I told her about was the fact that I was spending significant amount of time at that part of my life in training camps in various places in the world.
Peter Liljedahl: And there was a lot of high school students in these training camps and I kind of always became the unofficial camp tutor, helping students with math and physics and things like that. This seemed to appeal to her. So she hired me and I became a TA. I was finishing up my undergraduate degree and one of the people I’d gotten to know during that time, a guy by the name of Grant, said, “Hey, you should apply for the teacher education program.” And I thought, yeah, that’s a nice fallback position. It’s only a one year program. I can do that. It’s a nice backstop in case my career as a mathematics computer programmer didn’t quite come to fruition or whatever it was I was thinking at the time. So I entered the program, I got in, basically on the fact that I had these experiences as a TA and so on and fell in love with teaching, absolutely fell in love with it.
Peter Liljedahl: My first practicum that I had to go out for, I showed up, and my sponsor teacher, I literally walked in the door and he looked at me and said, “Oh hey, Peter, I think you can take this lesson.” It was like, I just fell in love with teaching. I thought, this is it. I’m going to be a math teacher for the rest of my life. I was teaching, in my practicum, I was all high school math courses, eight through 12, a lot of grade 12 calculus. They actually created a calculus course for me to teach with no supervision. It was kind of the Wild West. Anyway, and then I ended up getting a position in that same school.
Peter Liljedahl: So I was a high school math teacher. While I had been finishing off my math degrees, there was a number of mathematicians in the faculty who kept asking me to do a masters degree in math, and I’m like, “Are you kidding me? Who would ever want to get a masters degree? No thank you. If you give me things to solve and problems to solve, fine, but this idea of self initiated research questions, that is just craziness. There’s no way I would do a masters. About three or four years into my teaching, this brochure ended up in my mailbox at school for a masters program at SFU in math education. That was a joint program between the faculty of education and the math department. Like in many places in Canada, this was a concurrent degree, you continue to teach while you are doing your masters. All the courses were in the evening. It was all face-to-face contact. I applied and I got in and it was great. It was wonderful professional development, being able to see the same people, every Tuesday night, you were always together with the same people and it was great.
Kyle Pearce: Oh, interesting.
Peter Liljedahl: I’ve coordinated that masters program now for 14 years. Then one day I wanted to apply for a scholarship. So I emailed my supervisor and said, “Would you write me a reference letter?” And she says, “Well, why don’t you come in for a meeting?” So I came in for a meeting and she said, “So what are you doing these days?” At this point, I had also taken some time off from teaching to be a stay at home dad because we had two kids and my wife and I decided that that was important for one of us to do. So it was me, and I said, “Well this is what I’m doing.” She says, “Okay, well why don’t we do this? I will give you a reference letter for the scholarship application, but why don’t you transfer to the PhD program and come and work for me as a TA?”
Peter Liljedahl: I have a habit of saying yes, even when things are scary and …
Jon Orr: Twist my arm.
Peter Liljedahl: Off we went to the races. So I never actually finished my masters, but now I was in a PhD program and in my first year there came this opportunity to teach a course for pre-service elementary teachers, a methods course, and I applied and I got it. And it was like my first day of teaching again. I just absolutely fell in love with teaching teachers and stay away from the classroom. I was doing this graduate work with the intention of going back into the math classroom, but here I was working with adults working on the complexity of teaching and teaching practice and it was just this whole other ballgame. I fell in love with that. And then a whole bunch of things just fell into place. I did more and more teaching and eventually I finished my PhD and then there was a position available and I applied. That’s been my life for the last 15 years.
Kyle Pearce: That’s quite an interesting journey that you’ve just shared with us here. I know Jon’s probably there nodding as well. We’re actually in separate locations for those who think we’re in the same location right now. Your story sounds similar to Jon’s where he was kind of going that computer science route. I also, I actually started with a major in computer science and then I went to a double major and then eventually went down to a minor in the computer science and just focused on the math. So, interesting how those stories align. Now, I’m wondering, so it’s really interesting, you’ve taken some time to stay at home and help raise your two children, which I think is such an awesome thing and I’m sure an experience that you’ll always cherish having that opportunity.
Kyle Pearce: I’m wondering, before you decided to do that and you were in the classroom and then all of a sudden you come out, I’m assuming a handful of years later and now you’re in the pre-service, I’m wondering, do you have any thoughts on like, what did teaching look like, sound like to you? Maybe you might even want to go back to, what did math class look like, sound like to you? We always ask for our guests to share their memorable math moments. This might’ve been when you were younger, it could have been maybe in Sweden or maybe it was when you came over in Canada, but then also thinking about, when you were as a teacher in the classroom, were some of these ideas that you’ve been doing research around in these past handful of years, was that what your class looked like, sounded like or was this an evolution over time? I know lots of questions is loaded in there, but you’ve got me definitely very curious.
Peter Liljedahl: My memories of math in Sweden were … we would literally sit. I only did grade one in Sweden, but there was days where we worked in these notebooks that were graph paper, and we would open a page and the first page, every cell on the graph paper was filled with the number one. And we just spent like an hour writing the number one over and over and over again. Then the next day we would turn the page and we would do number two. Yeah.
Kyle Pearce: How were you [crosstalk 00:13:49]?
Jon Orr: You’re like [crosstalk 00:13:49]. Yeah.
Peter Liljedahl: Then there was a whole bunch of addition things. I do remember as a child figuring out what multiplication was and how it worked on my own. That has a lot to do with the language around multiplication in Swedish. That makes itself obvious what it’s meant to do. When I came to Canada it was …
Kyle Pearce: Do you mind elaborating on that? I’m actually curious, is it like a group sort of language or?
Peter Liljedahl: The language says, if you go three times four, it basically says three repeated four times. That’s the language of multiplication.
Jon Orr: I’m going to put you on the spot here. Can you speak Swedish?
Peter Liljedahl: Yeah.
Jon Orr: Yeah, I would love to hear it.
Peter Liljedahl: I can say in Swedish. I am fluent. [foreign language 00:14:34]. The language really pushed me in that direction, but it was a significant thing because I’d figured it out on my own. The rest of math elementary was very much what we would consider an ultra traditional classroom. There was a of direct instruction worksheets, lot of time drills, pass the paper to the person sitting behind you. The person at the back brings their paper to the front. A lot of public shaming, and that cuts both ways because people not performing well are being shamed, but people who are excelling are also being shamed in a world where it’s just not cool to be good at math.
Kyle Pearce: Right. So like maybe the other students pushing back on students doing well and just that negativity.
Peter Liljedahl: Right. I remember a couple of events where we were playing, this was grade five, we were playing this game where the teacher made everyone line up at the front of the room and then she would come down the line and ask a multiplication question. And if you’ve got it right, you could go and sit down and then if you got it wrong, you have to stay standing. We call it around the world.
Jon Orr: Yeah, around the world. It’s almost like opposite around the world.
Kyle Pearce: We still hear about it sometimes.
Peter Liljedahl: Yeah. have a lot of judgment about that, but nonetheless, I remember this one time the teacher asked me a question, I answered it, I answered it correctly. She said wrong and kept moving, and just the teasing that came with that, when the person who always gets it right all of a sudden got it wrong, and it was almost worse than the person who gets it wrong all the time. Right?
Kyle Pearce: I always remember as well in those types of scenarios, not necessarily the exact around the world, but just having to participate. Even though I was one of those kids that was lucky enough to be able to see some patterns and I could figure out the answer, I didn’t really understand in all cases, but I remember feeling very anxious just because it was like a performance. It was like, am I well enough rehearse to be able to open my mouth? Math class wasn’t really a social endeavor. It wasn’t a collaborative endeavor back then either. So very similar memory for me as well.
Peter Liljedahl: I think this is true of a lot of kids who Excel at mathematics. I saw the patterns in between. I saw the patterns despite the teaching that I was being exposed to and I started to find the efficiencies and so on and so forth. Then off the high school, which was grade eight for us, and I ended up having a situation where I had the same high school math teacher for grade eight, nine and 10. She didn’t really know what to do with me, so she just gave me the next year’s textbook. I sat at the desk and tried to figure out the patterns on my own. The last thing I was going to do is actually read the textbook. Just trying to spot the patterns and so on and so forth. She was a traditional lecturer. Stood at the overhead projector and lectured, and for the most part, I didn’t participate in that because I was trying to noodle my way through a grade 10 textbook and so on.
Jon Orr: , I think there’s a lot of these same stories from many people going through math. Are these stories that are kind of fueled you to do the research and the work that you’re doing now or is that a different kind of origin story?
Peter Liljedahl: No, but I think that’s a good question. What fuels me to do the work now is the realization that I’m one of the few who can do that. I was one of the 20% of kids who were going to survive math and excel at math despite what happens to them.
Kyle Pearce: It’s like you either are a math person or not ,and it’s like in that system that is the reality, but maybe it doesn’t have to actually be that way.
Peter Liljedahl: Right. I don’t believe it has to be that way, but it was that realization that … and I think that realization came when I was teaching, when I started teaching high school, that it was me saying it more clearly isn’t going to get this done.
Kyle Pearce: Now, how long did it take you to figure that out? Because I feel like, especially secondary teachers, and I know elementary, there’s a variety of different background stories, some elementary teachers got in because they love teaching math, others it’s like, “No, I got in because I just love working with kids.” And maybe math wasn’t my thing. But for secondary teachers, did you find that challenging to work with a group of students and students who are very … they come into our classroom in secondary with a very … their minds are made up on whether they like math, whether I’m a “math person” or not. When folks like yourself, and it sounds very similar to my experience and it sounds like Jon as well, we walk in and we sort of … it’s like we don’t know what it’s like to be on the other side where maybe it isn’t.
Kyle Pearce: Some of those patterns aren’t obvious or maybe some people haven’t been able to, let’s memorize the steps and procedures or whatever. What was that like for you walking into that secondary math classroom in order to be able to I guess empathize for the different variety of students at their different levels in the classroom?
Peter Liljedahl: I was privileged to work at a school. We had this ethos at the school as a math staff that everyone is going to go all the way in math. Back then, we only had two streams. We had the pre-calculus stream and then what we call the essential stream, which was carving people off into this cul-de-sac. We had this sort of ethos that no, everyone’s going to do pre-calc 12, we’re all going to get there. We had 200 kids. A typical grade 12 year, we would have seven blocks of pre-calc 12 and two blocks of calculus. There was maybe 10 kids in grade 12 who weren’t taking pre-calculus 12, and there was this real sort of community within the school that yeah, everyone can do it.
Peter Liljedahl: It was just this assumption that we’re all going to do this. There wasn’t anything like streaming where we were calling the weak people from the herd. We were getting the full rainbow and it’s not that the school was full of gifted students, it was a typical demographic, but now our teaching was really challenged by the fact that, okay, we got to work with this kid. Most of our math department was actually PE teachers who would teach one or two walks in math, and then there was a couple of-
Kyle Pearce: That’s an extra challenge for sure.
Peter Liljedahl: Well, yes and no. We had some people who were very good math teachers and some people who actually instilled a lot of self confidence in kids, which I think made our job easier when they would get up to grade 12 and so on. As a beginning teacher, I was stand and deliver. I had great board work and I had some good humor and my lecturing style was entertaining, I would say. There was certainly a group activity that would happen from time to time, but I always taught from a conceptual perspective, I never bought into the mnemonics or the memorize this. It was always conceptual. For example, one of the things I sent you an email was this unit circle superimposed on graph paper. This was something I started using when I was teaching trig in grade 12 was, we stopped using calculators for trig and we started using this piece of paper, and this piece of paper, scale, the way it is, and I would have stacks of this on my desk and the kids would do all their calculations using this.
Peter Liljedahl: If I asked them to figure out what the sign of 80 degrees was, knowing that sign is positive in certain quadrants and so on, they would, and a sign is the Y coordinate, they would be able to pull the Y coordinate off of this at 80 degrees. Conversely, if I asked them to solve cosine beta equals 0.6, they could use this graph with a superimposed circle on it to actually estimate what the angles were to within pretty accurate, within half a degree. I never had kids asking me, was this inverse sin or should it be sin?
Kyle Pearce: Right. Yeah, it was like they could see it. It was obvious when they see it conceptually.
Peter Liljedahl: Yeah, right. And tangent was a slope and it was completely conceptual and they would work on these papers and when it was so marked up that they couldn’t, all they needed was a ruler and a pencil. When it was all marked up to the point where they couldn’t work anymore, they’d throw it in the recycling and grab another sheet. It’s very conceptual this way. Not all my peers were doing this. They were teaching cast and and standard position angle. So I always had a very conceptual approach. I think getting back to your earlier question, the breakthrough moment for me was I was teaching this non AP calculus course. I really liked that course. It was an important course for me to teach because I didn’t think that the AP kids were the ones who actually needed a jump on calculus. It was the next level of kids who needed to have an inoculation into calculus, oh we could say.
Peter Liljedahl: I remember we were about halfway through the year and it was an early morning course, like it was a off calendar course or it was before school started and they needed to differentiate an exponential function. We had done implicit differentiation in trig and we had done inverse operations. This was technically doable. I remember I came in and I put up the question on the board, and I said, “Figure out how to do this, talk amongst yourselves.” They just sat there and stared at me and they wouldn’t move. It was like dead air, right? Like a dead air in a classroom just drags on forever.
Jon Orr: They’re just waiting for you to show them how to do it.
Peter Liljedahl: I’m realizing in this moment, holy cow, I’ve just been spoonfeeding these kids. I’m sure they can do it, they just don’t know that they can do it. So I stared at them in 30 seconds of dead air, and I finally just said, “I have to go do some photocopying.” And I left the room.
Kyle Pearce: That’s a good move.
Peter Liljedahl: I seen a portable. So I actually stood out in the parking lot and watched through the window and nobody moved and nobody talked. I stood out there for 15 minutes and I walk back in and I said, “Does anyone have anything to say?” And they all just stared at me and I just said, “I’ve got to go check the photocopying.” And I left again. I stood out in the parking lot for another 10 minutes. I came back in and I said, “Anything? They just stared at me. And I said, “Class dismissed.” Their jaws just dropped, and off they went. Then, the next morning when they came in, or it was two days later, they came in for class. All the boards were clear. The same question was written up on the front of the board, and I said, “Figure out how to do this, talk to each other. I got to go do some photocopy.”
Jon Orr: And they know the cat’s out of the bag there, that you don’t really have to do photocopying. They picked up on that pretty good.
Kyle Pearce: Yeah. This is not going to solve itself and I’m not going to be the one to do it either.
Peter Liljedahl: Yeah, and I stood in the parking lot for 35 minutes before anyone turned to each other and started talking. Now, this was long before I was doing any vertical surfaces or anything, so that sort of burst the bubble for me and I realized that, am I really doing these kids a service? Especially if they’re going to go off to university. The next test they wrote was a take home test. Again, their jaw dropped. I said, “Your unit test is going to be a take home test. You have to come here on Friday and sign saying that you will not cheat and then you take it and it’s due Monday morning.” It was 23 questions where the 23rd question was, how long did you spend on this test? The average was 20 hours. They came in on Monday morning and they were like, they were worked up. Then one of them said, “I see what you mean.” Because what I had done was put questions on here that they knew how to do, I just hadn’t shown them how to do it.
Kyle Pearce: Right. Planning with intentionality, and in my mind, something that I’m taking away from this is that, even though you were teaching conceptually, which I was not always doing a great job of, especially early in my career because I literally did not understand how some of the math actually work and develop, so in certain areas I was unable to do that. So, I was like teaching very procedurally in a lot of ways, but even in your situation where you were approaching things conceptually, which is amazing, which is awesome and really important, yet it was still again, you doing the work, “the work” and showing them the step by step and then leaving them in this position where they go, “I actually don’t know how to solve any unfamiliar problems.”
Kyle Pearce: I think this is a good segue, Jon has a question for you, some questions that he wanted to ask. So I think this is a great time for us to segue there, Jon. What are you thinking?
Jon Orr: Yeah, Peter, I’ve seen you live a number of times. Every time I listen to you, you always have these great messages and great suggestions for class and for changing the teaching in my room. I’ve put a lot of your suggestions into place. One of the last times I saw you, you had 14 ideas or 14 recommendations directly from your research, which hearing the research too, it almost backs us up to say like this is going to work. We’ve got people working on this to give us some evidence to see, to make sure that we are working in the right direction. What I love about the 14 recommendations that you have, some are very lesson specific like questioning and notes and types of problems.
Jon Orr: The other thing that I really love is that you also include recommendations for classroom setup and structure and grouping, which not a lot of people I think are doing, but I wonder if you could elaborate a little bit about what are the 14s. You could even start with, if there’s like a number one or even maybe the one you think is the most important.
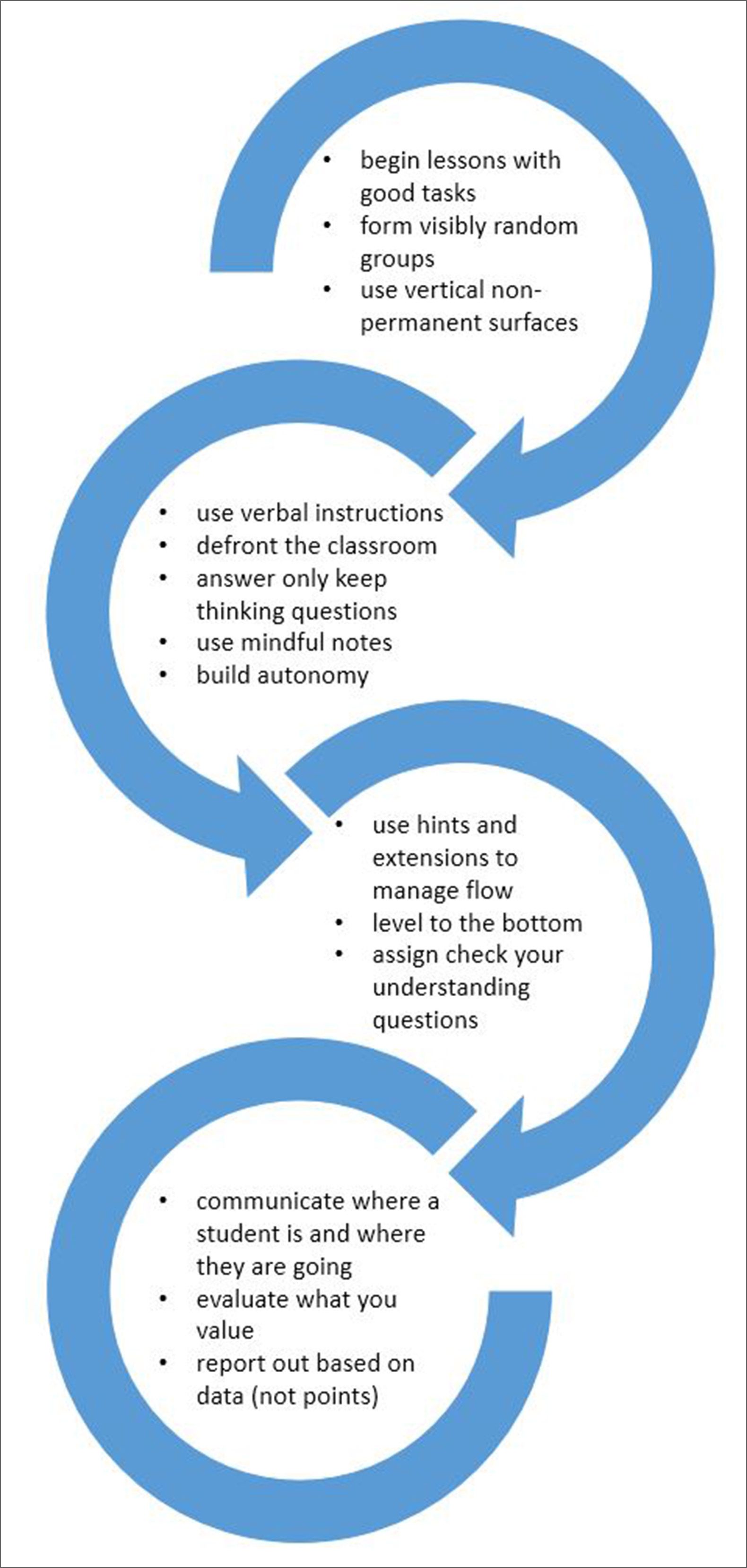
Peter Liljedahl: Okay. Before I do that, I’ll just say this. One of the things that motivated me to do that research was the realization that the institutionally normative structures of school were probably holding our kids back. The other thing I realized was all these years we’ve been doing professional development where we’re trying to change the teacher so the teacher can change the experience for the kids. The problem I realized was that the kids are the biggest stakeholders in this. Early efforts I was doing in professional development to try to change these norms was always through the teacher. All of the results were indicating, yeah, well, if the teacher is already doing problem solving, then this works. And if they’re not, then it doesn’t work. The kids had a lot more to say about what was going to work in the classroom and what the teacher was doing.
Peter Liljedahl: Part of this research was informed by trying to change the norms, and the other part, through the realization that we really got to create a new norm for the kids early on. This is where the vertical surfaces and the random groups and the rich tasks came in. That first wheel has those three things and they come very powerfully together. What they do is it creates a radically different normal for the kids so that the kids can be different, and that creates momentum. So yeah, the teacher has to do things different. What it does is it changes the kids, and it changes the kids and their experience in the room so quickly and so radically that now the teacher can start to do the work of changing their practice. Does that make sense?
Kyle Pearce: No, absolutely it does. It’s interesting to me because even just highlighting the vertical non-permanent surfaces, visible random grouping and then the idea of problem solving. I know some of these pieces are in these 14 recommendations that you have. I’m wondering, can you help, for someone who’s listening, going like, what is a vertical non-permanent surface? Really, if we think about what each word means, I think people would be able to figure it out, but it just sounds scary. What does that mean to you? Maybe, I don’t know, is there a specific reason why you use that language over maybe something else?
Peter Liljedahl: First of all, I should say that the first time I ever experienced that myself was as a teacher when my department had started dabbling with this. Then I did it and then I left it and then I didn’t come back to it until I was doing this research. It’s called a vertical non-permanent surface. That’s not what it was called to begin with. What it was called to begin with was a whiteboard, and not just any whiteboard. The research showed clearly that when we have the kids working in groups at whiteboards that are mounted on the wall, not little individual whiteboards or even bigger whiteboards at the table, we saw way more engagement across a whole bunch of different metrics, from eagerness to start to participation to perseverance.
Peter Liljedahl: The metrics were through the roof whenever we had the kids working in groups at vertical whiteboards. But teachers are incredibly innovative. When they started to find that this was really effective, but they were limited in resources, they started to improvise and we’ve learned that it worked just as well if we work on windows or if we duct taped up a shower curtain or stapled a vinyl picnic table cover onto our bulletin board, or if we stood our tables up on end or if we wrote on the side of a file cabinet.
Kyle Pearce: Now, is there a difference between a blackboard? Was there anything there? I’ve always made the assumption in my mind, maybe it’s just an assumption or maybe I’ve heard something a couple of years ago when I’ve seen you speak a few times. Is there anything about blackboard with chalk? Is there a pro con to that or would that just fit into this other grouping that you’ve highlighted here?
Peter Liljedahl: It fits in perfect. The only difference is that when we have the kids working on whiteboard or whatever surface, we only give them one marker and likewise you only get one piece of chalk. Well, they can break the chalk, so we have to make a whole bunch of noise around that so that they stay with one writing implemented. It forces a collaboration and the communication better.
Kyle Pearce: Yeah, so you’d have to have those norms very … Now, I don’t want to say structured, it sounds wrong, but just making sure that the community is strong enough where students don’t feel the need to sort of like try to get around that idea. Right?
Peter Liljedahl: Right. So like every time you break the chalk, the least loser game or something like that.
Kyle Pearce: A couple of years ago we didn’t have to do anything in the least we’re losing, but now it’s not so bad.
Peter Liljedahl: [crosstalk 00:32:13] back then. This notion of vertical non-permanent surfaces as a word or as a phrase, replace the notion of whiteboards because in order to honor the ingenuity of the teachers I was working with.
Jon Orr: I know you said that just because it’s vertical and non-permanent, what are your ideas on why that data is the way it is?
Peter Liljedahl: I love those why questions. One of the things that was amazing about this research was, in every instance, I had the results before I had the explanation, and this was of them. Vertical non-permanent surfaces came out number one in every metric. I had no idea why. Now came the fun part, right? Trying to unpack this and make sense of it. It turns out there’s a whole bunch of reasons why it’s better. One ergonomically, it turns out that having your head in an up position is better for you than having it tilted down. That’s a very subtle thing. It turns out that blood flow that’s promoted by having to stand is good for you. Also, very subtle.
Peter Liljedahl: It turns out that 50% of communication is nonverbal, right? So it’s done through gestures, and it turns out it’s easier to gesture when we’re standing than when we’re sitting. Also, very subtle. Some other subtle things. When we’re standing, every student in the group has the same orientation to the work and the ability to look at other people’s work. That’s not so subtle. That’s a really powerful stimulus for the students who are working in this setting.
Kyle Pearce: That’s interesting. When I’m on the phone even, I’m like a pacer. If I’m brainstorming, I tend to want to stand. Some of the pieces that you’ve just articulated there, just this idea of ergonomically, also the blood flow, I always felt it was the adrenaline. That’s your blood kind of doing its thing, right? Sending things where it needs to go. That makes a ton of sense to me for sure.
Peter Liljedahl: But all of those things were trumped by one other piece of research that emerged later on in the process. And it took a long time to get at this because there are kids who had a difficult time articulating, but it turns out it’s not that standing is so good, it’s that sitting is so bad. Not like sitting is the new smoking bad, but it turns out when the kids are sitting, they feel anonymous, and when they feel anonymous, they’re much more likely to disengage. That’s both a conscious and a subconscious act. Oh, a teacher can’t see me so I’m going to work on my social studies homework or that sort of subconscious pulling out the phone and looking at it, or just subconsciously disengaging.
Peter Liljedahl: Like I said, it took a while to get at this, but when they are sitting they feel anonymous. The further they are from the teacher, the more anonymous they feel. The more things that are between the teacher and that student, like desks and other students, the more anonymous they feel. All of a sudden we have them standing, spread out around the room, they don’t feel anonymous anymore.
Jon Orr: It’s almost like they have to have their A game out.
Peter Liljedahl: Yeah, but what’s interesting is they don’t feel like they’re being put on display or that it’s … it’s not a conscious feeling. It’s just that subconscious feeling of being able to disengage because you’re anonymous isn’t there anymore.
Kyle Pearce: Well, just even that culture of the room, there’s like that culture of collaboration when people are not sitting in desks. Even if you take those desks and put them in pairs, I used to do that when I tried to make my classroom more collaborative, but things were still very quiet and here it’s like you have movement and you have, almost that freedom, a little bit of that autonomy to walk around if you need to. If you want to go to another group to try to have a discussion over there, to me, I can see that idea and student voice and all of those pieces just fitting in so nicely here. I like how you’ve articulated that.
Peter Liljedahl: There’s a researcher in Israel who refers to these environments as choice rich environments.
Jon Orr: I want to go back just for a moment. When you were talking about the students being at the board and being able to say, “Look around the other boards.” When I bring vertical non-permanent surface ideas up to fellow teachers, some of them are saying, “Well, do you want them to look at everyone else’s work? Why aren’t they copying that work?” Even kids bring it up. They sometimes even will say like, “Am I supposed to look around at other people’s work?” What would you say to those teachers? How do you convince them to say like, “That’s actually beneficial for the kids?”
Peter Liljedahl: This was a concern of ours too. But what’s so interesting about it is, yeah, they look around, but they don’t steal finished work. What they steal are ideas so that they can get through the work and it’s fascinating to watch the way they’ll take an idea and then try to make it their own and use it to finish off. It’s really, really rare. I can maybe think of it twice where I’ve actually seen a group stand and just copy symbol for symbol from what another group has done. It’s just not what they do. It might be what they do early on when they think that the goal is to get done. When kids believe that the goal of the lesson is to get done a set of questions, then that’s how they behave. But in thinking classrooms, they very quickly pick up on that, the goal is to understand what you’re doing and to think your way through this and to use the resources in the room to get yourself to understanding this.
Kyle Pearce: It sounds to me, as well, that that’s where the role of the teacher also comes in, in terms of building that culture and making sure that your actions and your words align, right? Where if I’m saying I’m really interested in the process, but at the end I’m not valuing that through my actions, whether it be through assessment or whatever it might be, those mixed messages, they don’t jive together. So building that culture and really walking the walk when we say who cares about the idea. Then, I think it also goes right back to Jon’s initial question where it’s like, who cares if they copy it all? If they do, our problems much bigger than that. If I’m worried about them copying it, then I’m indicating that maybe I’m maybe leaning too hard on that answer piece versus that thinking process and convincing piece. Right? Getting students to be able to convince one another.
Jon Orr: It’s almost like a fine line to say like I’m doing vertical non-permanent surfaces at the wall and then when you have kids who work at the board and when you’re saying like what Kyle said, like what are the actions the teacher is making clear to the students? Because it’s saying like, once that problem is done, you can go back and sit down. All they’re going to do is want to be done, like you just said. Now, the goals, just from that one phrase, now the goal is to get done. So, that’s where it’s going to be like, “I’m just going to write that answer down and when he comes over he’s going to check off that I did it.” Instead of having that conversation with the group to talk about the thinking. There’s that fine line to say, I’m doing vertical non-permanent surfaces, but what are the actions that you are actually making clear to your students?
Peter Liljedahl: Right. The thinking classroom framework is 14 ways to build a thinking classroom. There’s about a hundred ways to screw it up. One really simple example of how thinking classrooms are so quickly messed up is, if I put up 10 questions on the board and I say, “Go to your vertical surfaces and do these 10 questions.” That sends a very strong message that the goal here is to get done those 10, and now whatever collaboration you may have fostered within the room and whatever you have built around meaning-making, it goes out the window. Because now the goal is to get done and a strong member of the group is going to grab the marker and off they go. So, it’s these subtle, what I call micro moves inside of each of these tools that are important as well around like having one marker instead of having three, having groups of three instead of groups of four, and so on and so forth. These are subtle things that we learned from the research that make it better.
Kyle Pearce: Right. Something that I hear out of that as well is, going back and saying, “Here’s 10 questions, go do them.” Jon and I, as you know, we talk a lot about curiosity. Really, there are so many different ways to build curiosity into your classroom. Something I always really respect about your work is that the tasks that you select, and I don’t want to go as far as to say that … it’s really tough to define a rich task because it’s really what you do with it, but the tasks that you provide up on your website and in your workshops that I’ve had the pleasure of attending, what I notice is that sometimes it’s not how the task is presented, sometimes people get tricked and think that what makes students curious is about how the question is presented, let’s say using a video or something along those lines.
Kyle Pearce: But what I noticed about your tasks is that many times you tell them like a story. You say it and then, it doesn’t necessarily seem curious at first, but as soon as you try one, like you just think about it just for a moment, all of a sudden, it’s like the challenge aspect of it. Like, you start to go, “Huh, there’s something going on here.” Again, it’s like now you’re captivated and you’re drawn in. How do you plan what sort of tasks you might do? If a teacher’s sitting at home listening to this going like, “Wow, I’ve never heard of vertical non-permanent, or maybe I have and I haven’t really understood how,” and they want to go try this, what are some things that you’re thinking about in order to select a task that might at least give me a good jumpstart on trying this in my own classroom?
Peter Liljedahl: Well, there’s two types of tasks that live in the thinking classroom. The one is what I call a rich task. Those are vital at the beginning part. Those are the ones we do in the workshops because coming in and doing a really exciting long division problem with a group of teachers isn’t really going to convey the message. For rich tasks, I look for a number of things, but we can use common lingo, a low floor, high ceiling, and things like this. What I really want is what I call evolving complexity. The further you get into the problem, the more complexities reveal themselves. Those evolving complexities are only accessed by the students who are getting through there as opposed to hitting them with complexity right out of the gate. These rich tasks, and I have a collection of them, and it turns out we need them early on when we’re building the culture and we also refer to them as non-curricular tasks because the goal is not to get through curriculum.
Peter Liljedahl: There are some resources out there that allow you to teach an entire curriculum through rich tasks. I really appreciate those, but that gets harder and harder to do the higher the grade goes. What those tasks do and when we’re introducing thinking classroom to students, as we start to get them into the habit of anticipating the next complexity and stealing the next question from another group around them and enjoying being in that space where we’re learning more and more and more, and the task is getting harder and harder and harder and we’re up for the challenge and this is fun. And really enjoying doing the thinking and the learning and the meaning-making. That’s the culture we’re trying to build. At the same time, that it’s a safe space, it’s collaborative, there’s lots of visuals around the room and other groups working.
Peter Liljedahl: There isn’t anyone focused on me. It’s a safe space to make mistakes because I can erase it because it’s a non-permanent surface. So it becomes a safe environment to start to forge ahead into this space. Then we slide into what I call the more curricular based tasks, which really are just tasks that we normally do with our classroom. Coming in and asking our students to factor a trinomial without me having taught them how to do it. Then, when they figure that one out, they get the next one, which is harder and the next one, which is harder yet and the next one, which is harder than that yet, and so on and so forth. Everything is the same about this experience as with a rich task, except what I’m doing now is I’m sort of hitting the curriculum head on, but it still has all those pieces.
Peter Liljedahl: It has an evolving complexity. as the coefficients change and the signs and the coefficients change. It has the opportunity to make meaning at every stage. It has a low floor if you set it up right. We can walk into this and we can all be successful at this level, but it is going to get harder and harder. My goal in thinking classrooms has always been not to build and find engaging tasks but to build engaged students that can then [crosstalk 00:44:20].
Kyle Pearce: That’s a show notes [inaudible 00:44:20] right there.
Peter Liljedahl: Then you point those engaged students at any content and they will think and engage and make meaning and engage in the evolving complexity. That’s what the game is here. That’s what the goal is.
Jon Orr: I think you’ve addressed a lot of questions that Kyle and I wanted to chat with you about here today because when we talk about teaching this way through task and engaging our students the way you’ve articulated it, and especially bringing out some of the tasks that you share on your website, teachers will say, “Yeah, that’s all great, but when am I supposed to do that?” Or, “I have to cover curriculum, I have to teach the curriculum expectations.” I want to summarize what you said like, for those teachers who have those kinds of questions, you’re saying like, work with the non curriculum tasks first, which can help build that culture, build that community in your classroom, and then slowly move into the curriculum or the curricular tasks that help engage them in that learning process.
Jon Orr: Then it’s not such a shock when, all of a sudden, they’re learning new stuff, but they’ve already been experienced to this new way of engaging their own learning. Would that be your recommendation to teachers who are like, :I don’t have that kind of time to teach this way.” I hear that a lot, especially in high school for sure.
Peter Liljedahl: I hear it a lot too and you’ve got to go slow to go fast. So taking that time early on to build the competencies, to build up the culture, to build the norms of the thinking classroom and then pointing them out at the thinking classroom pays off in spades. The longest it takes to do a unit on factoring quadratics is two days. It usually takes one day. Completing the square is usually a one day unit. Logarithms, we’ve gone through and … well, that one takes two days usually, sometimes three. We’re tearing through content once we get the students thinking. When students are not thinking, everything we teach is difficult.
Kyle Pearce: Right. Yeah, it’s because they don’t understand anything. There’s no learning is actually happening and you’re just spinning tires.
Peter Liljedahl: We got to cut the content into bite sized pieces and pre-do it for them.
Kyle Pearce: It’s interesting because I’m sitting here and there’s lots of head nodding. This is the one time that I wished that there was video on podcast because I’m sitting here and you can’t see my acknowledgement and my agreeance going on. But a few things, even going back to this non-curricular first idea to build that culture, it reminds me a lot of what Jon and I tend to suggest for teachers who haven’t used a notice and wonder in their classroom. We’re big on with curiosity. We like to push this idea of noticing and wondering and really getting kids to again think, but in a very nonthreatening way. Early on, like day one of the course, we say the same thing, which is, let’s just build the culture. We’ve got to do, and this is an investment.
Kyle Pearce: But then the other piece that I’m hearing from you as well is this idea of these non-curricular tasks might set off a red flag for a teacher, but at the end of the day, in most curriculums, whether it’s common core or here in Ontario where Jon and I are from, we have the process expectations, which when you look at those, those are the curriculum, and same with these mathematical practices for common core, and I’m sure in many other curriculums around, it’s not all content based, and yet, a lot of us sometimes just get hung up on that. Like you’re saying, by building that culture we get that huge payoff later where now we get to focus on teaching like where it matters instead of teaching all the surface stuff at where the kids are like peeling that stuff away really fast as they gain more confidence and engage in this culture in the classroom.
Peter Liljedahl: I had a masters student named Maria Kirkoff. She did her master’s thesis on, where the context was a thinking classroom, integrate 10 curriculum in British Columbia, and in BC, grade 10 is still a common curriculum. So we have almost all the kids together in a grade 10 class, so 18 days. For four weeks straight, all she did was rich tasks. None of this, let’s point on my core content, just rich tasks. There was a couple of holidays in there, so it ended up being 18 school days. So she did 18 rich tasks in 18 days and she tracked a student to see how much math they bumped into during those 18 days. By math, I mean both curricular math and what we call the competencies, which is like your processes.
Peter Liljedahl: In 18 days, she bumped into every grade 10 learning outcome except for two, a whole bunch from grade 11 and grade 12, a whole bunch from grade nine, eight, seven down to six, and had pretty much all of the competencies. So it was like if we could just do rich tasks, and I really firmly believe in that, I would love to be able to do just rich tasks. But my goal is to make every task rich. What determines whether a task is rich has a lot more to do with the disposition of the student than it does in the environment in which it’s done than it does the actual task. That’s what I’ve been working on.
Kyle Pearce: That’s awesome. I love how you use the term bumped into, because I find ourselves saying very similar things when we’re promoting this idea of trying to unitize or unsilo or desilo all of the curriculum and mix it up a little bit in order to promote more thinking and more problem solving, those resilient problem solvers. So, it’s great to hear that echoed in that description there.
Jon Orr: Peter, we know you are a busy man and we don’t want to take up too much of your time, but we have maybe just two more questions here. One, that we’re probably going to be trying to ask all of our guests near the end of the episodes, which is, just to give you a little background, in my class, I start each semester and end each semester with asking my students to complete a phrase, which is, “Math is like …” and then I just leave the dot, dot, dot, and their job is to kind of complete that sentence. What is it like and then explain why they say that. What is helpful for me, it gets everything out into the open in the first day of class, like where they’re coming from, some of the ideas that they bring with them, what are their thoughts on math.
Jon Orr: We have a good discussion about that to start setting our mindset. Then we end this semester, like we just ended our semester, our time of this recording, and so I always bring it back to see if anybody has changed after being in my class for a semester. We want to pose that to you. What is math like to you? If I said, “Math is like …” and then dot, dot, dot, what would you say?
Peter Liljedahl: Okay, before I answer that question, I have to tell you something that I do in my teaching. When I teach the undergraduates, the pre-service teachers, I always ask them four questions. I ask it to them on the first day, I ask it to them on the last day and I ask it to them on a day in the middle. The four questions are, what is mathematics? What does it mean to teach mathematics? What does it mean to learn mathematics? And did Peter teach today? Those are the four questions I get asked. I’ve actually written research papers on the results of that research and how their views and their beliefs change over time. If you want to ask me what mathematics is, I’m going to say mathematics is a verb and I can come at that from lots of different perspectives, but mathematics is also a noun.
Peter Liljedahl: I think many of the problems that we’re faced with in math education today lives in the tension between math as a noun in math as a verb. Is math the stuff that we have to learn or is it the doing? Curricular across Canada are more and more moving into the math as a verb, and yet, our external assessments is a lot about math as noun. That’s the tension we live in. For me, the content of a curriculum is just the context. The processes or the competencies are the content.
Kyle Pearce: That to me is very powerful. I love those four questions as well. Just thinking about that, and I’m picturing especially question number four, if someone comes into your class, pre-service teacher, and you don’t say nearly as much as what I’m used to a teacher saying, I might have very different perspective on whether you taught anything that day or not, and then by the end I’m certain that that would change quite dramatically. Peter, one more here and I just want to let you know we have a huge Google doc here of questions, and how silly of us to think that we were going to be able to dive into all 14 recommendations.
Jon Orr: I think we got through two.
Kyle Pearce: Yeah, we got through two, so I’m hoping maybe sometime in the future we’ll be able to invite you back on and dive into some of these others more deeply, but before we let you go, what are you working on right now? What’s keeping you curious in the teacher education space right now? Is there anything? Maybe it’s content focus, maybe it’s a verb or maybe it’s a noun, what’s on your mind currently?
Peter Liljedahl: Well, right now I’m writing up the book, Building Thinking Classrooms. So that’s keeping me busy and curious. I’m doing some research on tensions that teachers experience. One of my doctoral students is doing her thesis on that. I’m also spending some time with some international collaborators looking at some creativity in mathematics, which was a basis of my PhD thesis, breaking down some of the barriers around creativity. That’s sort of the space that I’m living in right now, but what’s keeping me curious in the thinking classroom framework is I am gearing up to spend a lot more time thinking about how this framework applies in other subject areas, and I’m still trying to understand why some things are the way they are in the thinking classroom framework.
Peter Liljedahl: I have a pretty good handle on the results of each of the pieces and why that is what it is, but this sequence of four toolkits of the 14 practices are embedded in is still fascinating me because that was an empirically emergent result, and trying to understand why some things are where they are in the sequence, and there are some new data that’s showing that maybe some of these are a little bit more flexible.
Kyle Pearce: I’m very excited to keep our ears to the ground and when your book comes out, I’m sure it’s going to be a very, very hot item out in the PD market for sure. Peter, thank you so much for joining us. That’s so great to hear. I know, where you are right now, things are a little bit nicer, not necessarily warm but warmer than where Jon and I are right now. So thank you so much for joining us. We can’t wait to share this episode with the rest of the math community, and hopefully, we’ll see you at a conference sometime soon.
Peter Liljedahl: Thank you for your time.
Jon Orr: Wow. Thanks so much, Peter, for joining us on The Making Math Moments That Matter Podcast. You dropped a bunch of math PD knowledge bombs on us during that interview.
Kyle Pearce: The biggest takeaway for me was how Peter suggested that teachers may want to consider starting with problems that are non-curricular in nature in order to build that culture of thinking in the classroom prior to building in the curricular focus tasks. It just goes to show how important building that culture in our classroom is, and it is an investment that’s going to reap huge rewards in the long run. Something for us all to keep front of mind. How about you Jon? What resonated with you?
Jon Orr: Yeah, there was a ton of things, but my biggest takeaway was how he said that there are 14 recommendations for the work that he’s doing with the thinking classroom and 100 ways to wreck it. It’s so important that we critically think about the things we say and do in our classrooms with students. I think gone are the days where I can just pull up an example or a problem and solve it, winging it without thinking about what questions I want to ask the students and what language and actions I need to show them. It’s, I think, so important that we critically think about these things going forward. I’m looking forward to having him back on the show to talk more about that and other parts of that thinking classroom.
Kyle Pearce: Awesome stuff. So how about you at home? What’s your big takeaway from this episode? Remember, you’ve got to share it with a friend. Maybe it’s a colleague or send us a message on social media at Make Math Moments on Twitter, Instagram, or Facebook.
Jon Orr: In order to ensure you don’t miss out on the new episodes as they come out each week, be sure to subscribe on iTunes or your favorite podcast platform.
Kyle Pearce: Also, if you’re liking what you’re hearing, please share the podcast with a colleague and help us reach an even wider audience by leaving us a review on iTunes and tweeting us @MakeMathMoments on Twitter. Show notes and links to resources from this episode can be found at makemathmoments.com/episode21. Again, makemathmoments.com/episode21. Well, until next time, I’m Kyle Pierce …
Jon Orr: And I’m Jon Orr.
Kyle Pearce: High fives for us …
Jon Orr: And high fives for you.

Thanks For Listening
- Apply for a Math Mentoring Moment
- Leave a note in the comment section below.
- Share this show on Twitter, or Facebook.
To help out the show:
- Leave an honest review on iTunes. Your ratings and reviews really help and we read each one.
- Subscribe on iTunes, Google Play, and Spotify.
Transcript Of The Peter Liljedahl Interview
Peter Liljedahl: So my goal in thinking classrooms has always been not to build and find engaging tasks, but to build and engage students that can then be pointed. And then you point those engaged students at any content, and they will think and engage, and make meaning [crosstalk 00:00:15].
Jon Orr: You’re listening to an interview with an influencer who has made a big impact on how we lead our lessons, and more importantly, how we structure our math classrooms. That’s right, today we’ll be spending some time with the man building thinking classrooms all over the world, Dr. Peter Liljedahl.
Kyle Pearce: In this Math Moment interview, we begin with Peter’s story that led him down the road to teaching secondary mathematics before shifting his focus to work with pre-service math teachers at Simon Fraser University in British Columbia, and engaging in research that is getting students standing and thinking in their math classes.
Jon Orr: This is episode number 21, The Thinking Classroom, an interview with Dr. Peter Liljedahl. Get ready to stand up, join your visible random grouping, and head over to the vertical non-permanent surface. It’s time to do some thinking. Start the intro music.
Kyle Pearce: Welcome to the Making Math Moments That Matter podcast. I’m Kyle Pearce.
Jon Orr: And I’m Jon Orr. We are two math teachers who together-
Kyle Pearce: With you, the community of educators worldwide who want to build and deliver math lessons that spark engagement-
Jon Orr: Fuel learning-
Kyle Pearce: And ignite teacher action. Well, I know I’m ready to go. How about you, Jon?
Jon Orr: For sure. We want to welcome Dr. Peter Liljedahl, professor of mathematics education at Simon Fraser University, who has been researching ways to get students to become resilient problem solvers through ideas such as using vertical non-permanent surfaces, visible random groupings, selecting tasks with evolving complexity, and much more. Well, it’s now the time to put that phone in your pocket, and listen to Peter give us some great insights.
Jon Orr: Hey there, Peter. How are you doing on this stormy day? Well, here in Ontario, anyway. How are you doing today?
Peter Liljedahl: I’m doing great. I just got back from South Africa yesterday, so today’s been more of a home day, taking care of business around the house, and catching up on email.
Kyle Pearce: South Africa. As we were just talking about before the recording started, but how hot was it there? They’re in their opposite season right now.
Peter Liljedahl: Yeah, 35 degrees.
Kyle Pearce: Jeez.
Jon Orr: Woo!
Peter Liljedahl: Yeah. A few days before I went, I was in Saskatoon where it was minus 31, so I think that’s a record for me for temperature swings across a short span of time.
Kyle Pearce: Well, that sounds like a pretty interesting math lesson around integers. You could have some fun there of sure.
Jon Orr: Why don’t we take a couple minutes here. Do you mind introducing yourself? I know many in the math community are aware of who you are, but what’s your role in math education? And what makes you tick when it comes to a math education and really trying to push thinking further in the math education space?
Peter Liljedahl: Well, I’m a professor at Simon Fraser University. I’m in the faculty of education. My unofficial title is Professor of Mathematics Education. I would say that I specialize in teaching and learning, meaning that most of my research and most of my own personal interest and curiosities lie within the ideas of teaching as informed by trying to motivate better learning in students. I’m a former high school math teacher, so my roots are in the classroom, and I think that has greatly informed my interests.
Jon Orr: Yeah.
Kyle Pearce: Well, I can only imagine.
Jon Orr: That sparks my interest right now, that kind of journey from high school math teacher to professor, or professor back to high school. Can you maybe fill us in on your say, math journey, even thinking back to when you were young? What did that path look like for you?
Peter Liljedahl: Okay, people may have noticed that my last name is not a typical Canadian last name. I was born in Sweden, and we immigrated to Canada when I was eight years old. When we did that, the only thing that I could really take with me was mathematics. I was pretty good at math in Sweden, but when I moved to Canada and entered grade 3, that was really the only place I could gain any footing, so I put a lot of energy there. And so, math became something. This idea of math as a universal language I guess is true in this regard. So yeah, math was always something that I was good at, I was interested in, I excelled at, I sometimes accelerated at. Went through high school, did very well in high school, and off to university.
Peter Liljedahl: It’s interesting, I just gave a talk to a group of students in high school the week before I went to South Africa. I was saying that when I graduated high school, my plan was simple. My plan was simple. I was going to go to UBC, University of British Columbia. I was going to get a degree in mathematics, and I was going to become a mathematician, whatever that meant. I had no clue what that meant.
Jon Orr: Yeah, I still don’t.
Peter Liljedahl: But I think this is one of the things that grade 12 students are often faced with when math is what they’re good at. What are you going to do with that? Part way through my math degree … and I took a long time to get my undergraduate degree. I was dabbling in sport at the time as well. But at some point, I realized that okay math I … I think I realized I wasn’t going to become a mathematician. I was getting a better idea of what that was. But I realized that math was my toolkit, but I had a topic to apply it to. So I started shifting into courses in computing science. I picked up a minor in computing science thinking that that would be the direction I would go in because that was a nice place to apply mathematics. I kind of realized that I liked programming a little bit too much, like obsessively too much. I was thinking that that was maybe not a healthy lifestyle choice.
Kyle Pearce: Were you actually coding, or just playing the games? Because I’ll take one a little more than the other.
Peter Liljedahl: I was coding. I was being a little bit of a perfectionist with it. Even when I had the code working exactly the way I wanted, I wanted it to be more compact and more efficient. Back then, memory was expensive and so on. It was about trying to make efficiencies which appealed to I guess the aesthetics of mathematics. There have been a number of circumstances by which I had some encounters with teaching mathematics during this time. One of which was, I’d be walking through the concourse at SFU. I had switched to SFU, by the way. I finished my undergraduate degree at Simon Fraser University, where I’m now a professor.
Peter Liljedahl: But I was walking through the concourse, and they had one of the bulletin boards is like, come be a TA in mathematics and calculus. It had the little strips of paper that you could teat off, so I pulled that off. I made a call, got an appointment. It was to be a TA at the university in the math department. I remember I showed up for the meeting, and the person interviewing me was a woman by the name of [Tusula Bergen 00:07:00], who is now the councilor general for Cypress in Canada, but she’s [inaudible 00:07:06]. She was a mathematician, and her husband was a mathematician in the math department. I remember I showed up for the meeting. She says, “Tell me a few things about yourself,” and I did. And she says, “You know, we don’t normally hire undergraduates. This ad was for graduate students.” And I said, “oh wow, okay, well thank you for your time.” And she goes, “No, no, no, tell me a little bit more about yourself.”
Peter Liljedahl: One of the things I told her about was the fact that I was spending significant amount of time at that part of my life in training camps in various places in the world, and there was a lot of high school students in these training camps. I kind of always became the unofficial camp tutor, helping students with math and physics and things like that. This seemed to appeal to her, so she hired me, and I became a TA. I was finishing up my undergraduate degree, and one of the people I had gotten to know during that time, a guy by the name of Grant said, “Hey, you should apply for the teacher education program.” I thought, yeah that’s a nice fallback position. It’s only a one year program, I can do that. It’s a nice backstop in case my career as a mathematics computer programmer didn’t quite come to fruition, or whatever it was I was thinking at the time.
Peter Liljedahl: I entered the program. I got in basically on the fact that I had these experiences as a TA, and so on, and fell in love with teaching. Absolutely fell in love with it. My first practicum that I had to go ut for, I showed up and my sponsor teacher … i literally walked in the door, and he looked at me and said, “Oh hey, Peter, I think you can take this lesson.” It was like, I just fell in love with teaching. I thought this is it, I’m going to be a math teacher for the rest of my life. I was teaching in my practicum, I was all high school math courses, 8 through 12. A lot of grade 12 calculus. They actually created a calculus course for me to teach with no supervision. It was kind of the wild west. Anyway, and then I ended up getting a position in that same school, so I was a high school math teacher.
Peter Liljedahl: While I had been finishing up my math degrees, there was a number of mathematicians in the faculty who kept asking me to do a master’s degree in math, and I’m like, “Are you kidding me? Who would ever want to get a master’s degree? No thank you.” If you give me things to solve and problems to solve, fine. But this idea of self-initiated research questions, that is just craziness. There’s no way I would do a master’s. About three or four years into my teaching, this brochure ended up in my mailbox at school for a master’s program at SFU in math education. It was a joint program between the faculty of education and the math department. Like in many places in Canada, this was a concurrent degree. You continue to teach while you are doing your master’s. All the courses were in the evening. It was all face-to-face contact, so I applied and I got in, and it was great. It was wonderful professional development being able to see the same people. Every Tuesday night, you were always together with the same people, and it was great.
Kyle Pearce: Oh, interesting.
Peter Liljedahl: I’ve coordinated that master’s program now for 14 years. And then one day I wanted to apply for a scholarship, so I emailed my supervisor and said, “Would you write me a reference letter?” And she says, “Well why don’t you come in for a meeting?” I came in for a meeting and she said, “So what are you doing these days?” At this point, I had also taken some time off from teaching to be a stay at home dad because we have two kids, and my wife and I decided that that was important for one of us to do. So it was me. I said, “Well this is what I’m doing.” She says, “Okay, well why don’t we do this? I will give you a reference letter for the scholarship application, but why don’t you transfer to the PhD program, and come and work for me as a TA?” I have a habit of saying yes even when things are scary. Yeah.
Kyle Pearce: Twist my arm.
Peter Liljedahl: So off we went to the races. I never actually finished my master’s. By now I was in a PhD program, and in my first year, there came this opportunity to teach a course for pre-service elementary teachers, a methods course. I applied and I got it, and it was like my first day of teaching again. I just absolutely fell in love with teaching teachers. Stay away from the classroom … I was doing this graduate work with the intention of going back into the math classroom, but here I was working with adults, working on the complexity of teaching and teaching practice. It was just this whole other ballgame, and I fell in love with that. And then a whole bunch of things just fell into place. I did more and more teaching, and eventually I finished my PhD, and then there was a position available, and I applied. That’s been my life for the last 15 years.
Kyle Pearce: That’s quite an interesting journey that you’ve just shared with us here. I know Jon’s probably there nodding as well. We’re actually in separate locations, for those who think we’re in the same location right now. Your story sounds similar to Jon’s, where he was kind of going that computer science route. I actually started with a major in computer science, and then I went to a double major, and then eventually went down to a minor in the computer science, and just focuses on the math. Kind of interesting how those stories align. Now, I’m wondering, it’s really interesting you’ve taken some time to stay at home and help raise your two children, which I think is such an awesome thing and I’m sure an experience that you’ll always cherish, having that opportunity.
Kyle Pearce: I’m wondering, before you decided to do that, and you were in the classroom, and then all of a sudden you come out, I’m assuming a hand full of years later, and now you’re in the pre-service, I’m wondering do you have any thoughts on what did teaching look like, sound like to you? Maybe you might even want to go back to what did math class look like, sound like to you? We always ask for our guests to share their memorable math moments, so this might have been when you were younger, it could have been maybe in Sweden, or maybe it was when you came over in Canada. But then also, thinking about when you were a teacher in the classroom, were some of these ideas that you’ve been doing research around in these past handful of years, was that what your class looked like, sounded like? Or was this sort of an evolution over time? I know, lots of questions loaded in there, but you’ve got me definitely very curious.
Peter Liljedahl: My memories of math in Sweden were, we would literally sit … I only did grade 1 in Sweden, but there was days where we worked in these notebooks that were graph paper, and we would open a page, and the first page, every cell on the graph paper was filled with the number one. We just spent an hour writing the number one over, and over, and over again. And then the next day, we would turn the page, and we would do number two. Yeah, well, yeah-
Jon Orr: How are you at reading the number one, now, though?
Kyle Pearce: Were they-
Peter Liljedahl: [crosstalk 00:13:49]. Yeah.
Jon Orr: You’re dashing lines you had to trace?
Peter Liljedahl: And then there was a whole bunch of addition things. I do remember as a child, figuring out what multiplication was and how it worked, on my own. That has a lot to do with the language around multiplication in Swedish, that makes itself obvious what it’s meant to do. When I came to Canada, it was-
Jon Orr: To you mind elaborating on that? I’m actually kind of curious. Is it a group sort of language?
Peter Liljedahl: Well, the language kind of says if you go three times four, it basically says three, repeated four times. That’s the language of multiplication.
Jon Orr: I’m going to put you on the spot here. Can you speak Swedish?
Peter Liljedahl: Yeah.
Jon Orr: Yeah, I would love to hear it.
Peter Liljedahl: I can say it, yeah I am fluent. [Swedish 00:14:33]. The language really sort of pushed me in that direction, but it was kind of a significant thing because I had figured it out on my own. I think the rest of math elementary was very much what we would consider ultra traditional classroom. There was a lot of direct instruction worksheets, a lot of timed drills, pass a paper to the person sitting behind you, the person at the back brings your paper to the front. A lot of public shaming. That cuts both ways because people not performing well or being shamed, or people who are excelling are also being shamed in a world where it’s just not cool to be good at math, right?
Kyle Pearce: Right. Maybe the other students kind of pushing back on students doing well, and just that negativity.
Peter Liljedahl: Right. If you happen to make a single … I remember a couple of events where we were playing. This was grade 5. We were playing this game where the teacher made everyone line up at the front of the room, and then she would come down the line and ask a multiplication question. If you got it right, you could go and sit down. And then if you got it wrong, you had to stay standing. We call it, around the world.
Jon Orr: Yeah, around the world. It’s almost the opposite-
Kyle Pearce: Around the world, yeah.
Jon Orr: … around the world.
Kyle Pearce: You still hear about it sometimes, you know?
Peter Liljedahl: Oh, yeah. I have a lot of judgment about that. But nonetheless, I remember this one time the teacher asked me a question, I answered it, I answered it correctly. She said, “Wrong,” and kept moving. Just the teasing that came with that when the person who always gets it right all of a sudden got it wrong. It was almost worse than the person who gets it wrong all the time.
Kyle Pearce: I always remember as well in those types of scenarios, not necessarily the exact around the world, but just having to participate even though I was one of those kids that was lucky enough to be able to see some patterns in it, I could figure out the answer, I didn’t really understand in all cases but I remember feeling very anxious just because it was like a performance. It was like, am I well enough rehearsed to be able to open my mouth? Math class wasn’t really a social endeavor. It wasn’t a collaborative endeavor back then either, so very similar memory for me as well.
Peter Liljedahl: I think this is true of a lot of kids who excel at mathematics. I saw the patterns in between. I saw the patterns despite the teaching that I was being exposed to. I started to find the efficiencies, and so on and so forth. And then off to high school, which was grade 8 for us. I ended up having a situation where I had the same high school math teacher for grade 8, 9 and 10. She didn’t really know what to do with me, so she just gave me the next year’s textbook. I sat at the desk and tried to figure out the patterns on my own. The last thing I was going to do was actually read the textbook. Just trying to spot the patterns, and so on and so forth. She was a traditional lecturer, stood at the overhead projector and lectured. For the most part, I didn’t participate in that because I was trying to noodle my way through a grade 10 textbook, and so on.
Kyle Pearce: These stories, I think there’s a lot of these same stories for many people going through math. Are these stories that have fueled you to do the research and the work that you’re doing now? Or is that a different kind of-
Peter Liljedahl: I think that-
Kyle Pearce: … origin story?
Peter Liljedahl: No, no, no but I think that’s a good question. What’s fueled me to do the work right now is the realization that I am one of the few who can do that. I was one of the 20% of kids who are going to survive math and excel at math despite what happens to them. And not-
Kyle Pearce: So it’s like you either are a math person or not, and it’s like in that system, that is the reality, but maybe it doesn’t have to actually be that way.
Peter Liljedahl: Right. I don’t believe it has to be that way, but it was that realization that … and I think that realization came when I was teaching, when I started teaching high school. It was like me saying it more clearly isn’t going to get this done.
Kyle Pearce: Now, how long did it take you to figure that out? Because I feel like especially secondary teachers, and I know elementary there’s a variety of different background stories. Some elementary teachers got in because they love teaching math. Others it’s like, no I got in because I just love working with kids, and maybe math wasn’t my thing. But for secondary teachers, did you find that challenging to work with a group of students? Students who are very … they come into our classroom in secondary with a very sort of, their minds are made up on whether they like math, whether I’m “a math person,” or not. When folks like yourself … and it sounds very similar to my experience, and it sounds like Jon as well. We walk in and it’s like we don’t know what it’s like to be on the other side where maybe some of those patterns aren’t obvious, or maybe some people haven’t been able to, let’s memorize the steps and procedures, or whatever.
Kyle Pearce: What was that like for you walking into that secondary math classroom in order to be able to, I guess, empathize for the different variety of students at their different levels in the classroom?
Peter Liljedahl: I was kind of privileged to work at a school. We had this ethos at the school as a math staff that everyone is going to go all the way in math. Back then, we only had two streams. We had the pre calculus stream, and then what we called the essential stream, which was carving people off into this cultisac. We had this ethos that no, everyone’s going to do precal 12. We’re all going to get there. We had 200 kids, and in a typical grade 12 year we would have seven blocks of pre-calc 12, and two blocks of calculus. There was maybe 10 kids in grade 12 who weren’t taking pre calculus 12. There was this real community with the school that, yeah, everyone can do it. It was just this assumption that we’re all going to do this. There wasn’t anything like streaming where we were calling the weak people from the herd. We were getting the full rainbow. It’s not that the school was full of gifted students. It was a typical demographic, but now our teaching was really challenged by the fact that okay, we got to work with these kids.
Peter Liljedahl: Most of our math department was actually PE teachers who would teach one or two blocks in math. And then there was a couple of-
Kyle Pearce: That’s an extra challenge for sure.
Peter Liljedahl: Well, yes and no. We had some people who were very good math teachers, and some people who actually instilled a lot of self-confidence in kids, which I think made our job easier when they would get up to grade 12, and so on. As a beginning teacher, I was stand and deliver. I had great board work, and I had some good humor, and my lecturing style was entertaining, I would say. There was certainly group activity that would happen from time to time, but I always taught from a conceptual perspective. I never bought into the gnomonics, or the memorize this. It was always conceptual. For example, one of the things I sent you in email was this unit circle superimposed on graph paper. This was something I started using when I was teaching trig in grade 12, was we stopped using calculators for trig, and we started using this piece of paper. This piece of paper, scaled the way it is.
Peter Liljedahl: I would have stacks of this on my desk. The kids would do all their calculations using this. If I asked them to figure out what the sign of 80 degrees was, knowing that sign is positive in certain quadrants and so on, and the sign is the Y coordinate, they would be able to pull the Y coordinate off of this at 80 degrees. Conversely, if I asked them to solve cosine beta equals zero point six, they could use this graph with a superimposed circle on it to actually estimate what the angles were, to within pretty accurate, to within half a degree. I never had kids asking me, “Was this an inverse sign? Or should it be sign”?
Kyle Pearce: Right, right. Yeah, it was like they could see it. It was obvious, when they see it conceptually, right?
Peter Liljedahl: Yeah. Right. Tangent was the slope, and it was completely conceptual, and they would work on these papers. When it was so marked up that they couldn’t … All they needed was a ruler and a pencil, and when it was all marked up to the point where they couldn’t work it anymore, they’d through it in the recycling and grab another sheet. Very conceptual this way. Not all my peers were doing this. They were teaching caste and standard position angle. I always had a very conceptual approach. I think getting back to your earlier question, the breakthrough moment for me was I was teaching this non AP calculus course. I really like that course. It was an important course for me to teach because I didn’t think that the AP kids were the ones who actually needed a jump on calculus. It was the next level of kids who needed to have an inoculation into calculus, you could say. I remember we were about halfway through the year, and it was an early morning course. It was an off calendar course, so it was before school started.
Peter Liljedahl: They needed to differentiate an exponential function. We had done implicit differentiation in trig, and we done inverse operations, so this was technically doable. I remember I came in, and I put up the question on the board, and I said, “Figure out how to do this. Talk amongst yourselves,” and they just sat there and stared at me. They wouldn’t move. It was like dead air. Dead air in a classroom just drags on forever.
Kyle Pearce: They’re just waiting for you to show them how to do it?
Peter Liljedahl: Yeah. I’m realizing in this moment, holy cow, I’ve just been spoon feeding kids. They don’t know. I’m sure they can do it, they just don’t know that they can do it. I stared at them, and 30 seconds of dead air, and I finally just said, “I have to go do some photocopying,” and I left the room.
Kyle Pearce: Yeah, that’s a good move.
Peter Liljedahl: I was teaching in a portable, so I actually stood out in the parking lot and watched through the window, and nobody moved, and nobody talke.d I stood out there for 15 minutes, and I walked back in, and I said, “Does anyone have anything to say?” They all just stared at me. I just said, “I got to go check the photocopying,” and I left again. I stood out in the parking lot for another 10 minutes. I came back in and I said, “Anything?” They just stared at me, and I said, “Class dismissed.” Their jaws just dropped, and off they went. And then the next morning when they came in, or it was two days later they came in for class, all the boards were clear. The same question was written up on the front of the board. I said, “Figure out how to do this. Talk to each other. I got to go do some photocopying.”
Jon Orr: And now the cats out of the bag there that you don’t really have to do photocopying. They picked up on that pretty good.
Kyle Pearce: Yeah, this is not going to solve itself, and I’m not going to be the one to do it either.
Peter Liljedahl: Yeah. I stood in the parking lot for 35 minutes before anyone turned to each other and started talking. Now this was long before I was doing any vertical surfaces or anything, so that sort of burst a bubble for me and I realized that, am I really doing these kids a service? Especially if they’re going to go off to university. And so the next test they wrote was a take home test. And again, they’re jaw dropped. I said, “Your unit test is going to be a take home test. You have to come here on Friday and sign saying that you will not cheat, and then you take it, and it’s due Monday morning.” It was 23 questions where the 23rd question was, “How long did you spend on this test?”
Peter Liljedahl: The average was 20 hours. They came in on Monday morning and they were worked up. And then one of them said, “I see what you mean.” Because what I had done was put questions on here that they knew how to do, I just hadn’t shown them how to do it.
Kyle Pearce: Right, so planning with intentionality. In my mind, something that I’m taking away from this is that even though you were teaching conceptually, which I was not always doing a great job of especially earlier in my career because I literally did not understand how some of the math actually worked and developed. So in certain areas, I was unable to do that, so I was teaching very procedurally in a lot of ways. But even in your situation where you were approaching things conceptually, which is amazing, which is awesome and really important, yet it was still again, you doing “the work” and showing them the step-by-step, and then leaving them in this position where they go, “I actually don’t know how to solve any unfamiliar problems.”
Kyle Pearce: I think this is a good segue. Jon has a question for you, it’s some questions that he wanted to ask, so I think this is a great time for us to segue there. Jon, what are you thinking?
Jon Orr: Yeah. Peter, I’ve seen you live a number of times. Every time I listen to you, you always have these great messages and great suggestions for class, and for changing the teaching in my room. I’ve put a lot of your suggestions into place. One of the last times I saw you, you had 14 ideas or 14 recommendations directly from your research. Which, hearing the research too, it almost backs us up to say, this is going to work, we’ve got people working on this to give us some evidence to make sure that we are working in the right direction. What I love about the 14 recommendations that you have, some are very lesson specific, questioning and notes, and types of problems. But the other thing that I really love is that you also include recommendations for classroom setup, and structure, and grouping, which not a lot of people I think are doing.
Jon Orr: But I wonder if you could elaborate a little bit about what are the 14. You could even start with if there’s a number one, or even maybe the one you think is the most important.
Peter Liljedahl: Okay, before I do that I’ll just say this, one of the things that motivated me to do that research was the realization that the institutionally normative structures of school were probably holding our kids back. The other thing I realized was all these years we’ve been doing professional development where we’re trying to change the teacher so the teacher can change the experience for the kids, the problem I realized was that the kids are the biggest stakeholders in this. Early efforts I was doing in professional development to try to change these norms was always through the teacher. All of the results were indicating, yeah well if the teacher’s already doing problem solving, then this works. And if they’re not, then it doesn’t work. The kids had a lot more to say about what was going to work in the classroom than what the teacher was doing.
Peter Liljedahl: Part of this research was informed by trying to change the norms, and the other part through the realization that we really got to create a new norm for the kids early on. This is where the vertical surfaces and the random groups, and the rich tasks came in. That first wheel has those three things. They come very powerfully together. What they do is it creates a radically different normal for the kids so that the kids can be different. That kind of creates momentum. So yeah, the teacher has to do things different. What it does is it changes the kids, and it changes the kids and their experience in the room so quickly and so radically that now the teacher can start to do the work of changing their practice. Does that make sense?
Kyle Pearce: No, absolutely it does. It’s interesting to me because even just highlighting the vertical non permanent surfaces, visible random grouping, and then the idea of problem solving. I know some of these pieces are in these 14 recommendations that you have. I’m wondering, for someone who’s listening going, “What is a vertical non permanent surface?” Really, if we think about what each word means, I think people would be able to figure it out, but it just sounds kind of scary. What does that mean to you? Maybe, I don’t know, is there a specific reason why you use that language over maybe something else?
Peter Liljedahl: First of all, I should say that the first time I ever experienced that myself was as a teacher when my department had started dabbling with this. And then I did it, and then I left it, and then I didn’t come back to it until I was doing this research. It’s called a vertical non permanent surface. That’s not what it was called to begin with. What it was called to being with was a whiteboard, and not just any whiteboard. The research showed clearly that when we had the kids working in groups at whiteboards that are mounted on the wall, not little individuals or even bigger whiteboards at the table, we saw way more engagement across a whole bunch of different metrics from eagerness to start, to participation, to perseverance. The metrics were through the roof whenever we had the kids working in groups at vertical whiteboards.
Peter Liljedahl: But teachers are incredibly innovative. When they started to find that this was really effective, but they were limited in resources, they started to improvise, and we learned that it worked just as well if we worked on windows or if we duct taped up a shower curtain, or stapled a vinyl picnic table cover onto our bulletin board, or if we stood our tables up on end, or if we wrote on the side of a file cabinet.
Kyle Pearce: Now, is there a difference between a blackboard? Was there anything there? I’ve always made the assumption in my mind … maybe it’s just an assumption, or maybe I heard something when I have seen you speak a few times. Is there anything about a blackboard with chalk, is there a pro/con to that? Or would that just fit into this other grouping that you’ve highlighted here?
Peter Liljedahl: If it’s imperfect, the only difference is that when we have the kids working on whiteboard or whatever surface, we only give them one marker. Likewise, they only get one piece of chalk. Well, they can break the chalk, so we have to make a whole bunch of noise around that so that they stay with one writing implement. It forces a collaboration of communication better.
Kyle Pearce: Yeah, so you’d have to have those norms. I don’t want to say structured, it sounds wrong. But just making sure that the community is strong enough where students don’t feel the need to try to get around that idea, right?
Peter Liljedahl: Right. Every time you break the chalk, the Leafs lose a game, or something like that.
Kyle Pearce: A couple years ago, we didn’t have to do anything, and the Leafs were losing. But now, it’s not so bad.
Peter Liljedahl: There was a lot of chalk being broken back then. So, this notion of vertical non permanent surfaces as a word or as a phrase replaces the notion of whiteboards because in order to honor the ingenuity of the teachers I was working with.
Kyle Pearce: I know you said that just because it’s vertical and non permanent, what are your ideas on why that data is the way it is?
Peter Liljedahl: I love those why questions. One of the things that was amazing about this research was, in every instance I had the results before I had the explanation. This was one of them. Vertical non permanent surfaces came out number one in every metric. I had no idea why. Now came the fun part, trying to unpack this and make sense of it. It turns out there’s a whole bunch of reasons why it’s better. One, ergonomically. It turns out that having your head in a up position is better for you than having it tilted down. That’s a very subtle thing. It turns out that blood flow that’s promoted by having to stand is good for you. Also, very subtle. It turns out that 50% communication is non verbal. It’s done through gestures. It turns out it’s easier to gesture when we’re standing than when we’re sitting. Also, very subtle.
Peter Liljedahl: Some other subtle things. When we’re standing, every student in the group has the same orientation to the work, and the ability to look at other people’s work. That’s not so subtle. That’s a really powerful stimulus for the students who are working in this setting.
Kyle Pearce: That’s interesting. When I’m on the phone even, I’m a pacer. If I’m brainstorming, I tend to want to stand. Some of the pieces that you’ve just articulated there, just this idea of ergonomically, also the blood flow, I always felt it was the adrenaline. But that’s your blood doing it’s thing, sending things where it needs to go. That makes a ton of sense to me for sure.
Peter Liljedahl: But all of those things were trumped by one other piece of research that emerged later on in the process. It took a long time to get at this because the kids had a difficult time articulating. But it turns out it’s not that standing is so good, it’s that sitting is so bad. Not like sitting is the new smoking bad, but it turns out when the kids are sitting, they feel anonymous. When they feel anonymous, they are much mote likely to disengage. That’s both a conscious and a subconscious act. So, oh the teacher can’t see me so I’m going to work on my social studies homework, or that subconscious pulling out the phone and looking at it, or just subconsciously disengaging.
Peter Liljedahl: Like I said, it took a while to get at this, but when they are sitting, they feel anonymous. The further they are from the teacher, the more anonymous they feel. The more things that are between the teacher and that student like desks and other students, the more anonymous they feel. All of a sudden we have them standing spread out around the room, they don’t feel anonymous anymore.
Kyle Pearce: That’s almost like they have to have their A game out.
Peter Liljedahl: Yeah. But what’s interesting is they don’t feel like they’re being put on display or that it’s not a conscious feeling, it’s just that subconscious feeling of being able to disengage because your anonymous isn’t there anymore.
Kyle Pearce: Well, just even that culture of the room. There’s that culture of collaboration when people are not sitting in desks. Even if you take those desks and put them in pairs. I sued to do that when I tried to make my classroom more collaborative, but things were still very quiet. Here, it’s like you have movement, and you have almost that freedom, a little bit of that autonomy to walk around if you need to, if you want to go to another group to try to have a discussion over there. To me, I can see that idea and student voice, and all of those pieces just fitting in so nicely here. I like how you’ve articulated that.
Peter Liljedahl: There’s a researcher in Israel who refers to these environments as choice rich environments.
Kyle Pearce: I want to go back just for a moment. You were talking about the students being at the board and being able to say, “Look around the other boards.” When I bring vertical non permanent surface ideas up to fellow teachers, some of them are saying, “Well, do you want them to look at everyone else’s work? Why aren’t they copying that work?” Even kids bring it up. They sometimes even will say, “Am I supposed to look around at other people’s work?” What would you say to those teachers? How do you convince them to say, “That’s actually beneficial for the kids?”
Peter Liljedahl: This was a concern of ours too, but what’s so interesting about it is, yeah, they look around but they don’t steal finished work. What they steal are ideas so that they can get through the work. It’s fascinating to watch the way they’ll take an idea and then try to make it their own, and then use it to finish off. It’s really, really rare. I can maybe think of twice where I’ve actually seen a group stand and just copy symbol for symbol from what another group has done. It’s just not what they do. It might be what they do early on when they think that the goal is to get done. When kids believe that the goal of the lesson is to get done a set of questions, that’s how they behave.
Peter Liljedahl: But in thinking classrooms, they very quickly pick up on that the goal is to understand what you’re doing, and to think your way through this, and to use the resources in the room to get yourself to understanding this.
Kyle Pearce: It sounds to me as well that, that’s where the tole of the teacher also comes in, in terms of building that culture and making sure that your actions and your words align, where if I’m saying, “I’m really interested in the process,” but at the end I’m not valuing it through my actions. Whether it be through assessment or whatever it might be, those mixed messages, they don’t jive together. Building that culture and really walking the walk when we say, “Who cares about the idea?” And then I think it also goes right back to Jon’s initial question where it’s like, who cares if they copy it all? If they do, our problem’s much bigger than that. If I’m worried about them copying it, then I’m sort of indicating that maybe I’m leaning too hard on that answer piece versus that thinking process and convincing piece, getting students to be able to convince one another.
Jon Orr: It’s almost like a fine line to say, “I’m doing vertical non permanent surfaces at the wall,” and then when you have kids who work at the board. When you’re saying like what Kyle said, “What are the actions the teacher is making clear to the students?” Because in saying, “Once that problem’s done, you can go back and sit down,” all they’re going to do is want to be done, like you just said. Just from that one phrase, now the goal is to get done. And so, that’s where it’s going to be like, I’m just going to write that answer down, and when he comes over, he’s going to check off that I did it instead of having that conversation with the group, just talk about the thinking. There’s that fine line to say, “I’m doing vertical non permanent surfaces, but what are the actions that you are actually making clear to your students?”
Peter Liljedahl: Right. The thinking classroom framework is 14 ways to build a thinking classroom. There’s about 100 ways to screw it up. One really simple example of how thinking classrooms are so quickly messed up is if I put up 10 questions on the board and I say, “Go to your vertical surfaces and do these 10 questions,” that sends a very strong message that the goal here is to get done those 10. And now whatever collaboration you may have fostered within the room, whatever you have built around meaning making, it goes out the window. Because now the goal is to get done, and the strong member of the group is going to grab the mark, and off they go. It’s the subtle, what I call micro moves inside of each of these tools that are important as well around having one marker instead of having three, having groups of three instead of groups of four. And so on, and so forth. These are subtle things that we learn from the research that make it better.
Kyle Pearce: Right, right. Something that I hear out of that as well is, going back and saying, “Here’s 10 questions, go do them.” Jon and I, and as you know we talk a lot about curiosity and really there are so many different ways to build curiosity into your classroom. Something I always really respect about your work is that the tasks that you select. I don’t want to go as far as to say that every … it’s really tough to define a rich task because it’s really what you do with it, but the tasks that you provide up on your website and in your workshops that I’ve had the pleasure of attending, what I notice is that sometimes it’s not how the task is presented. Sometimes people get tricked and think that what makes students curious is about how the question is presented, let’s say using a video or something along those lines. But what I noticed about your tasks is that many times you tell them a story. You say it, and then it doesn’t necessarily seem curious at first. But as soon as you try one, you just think about it just for a moment, all of a sudden it’s like the challenge aspect of it.
Kyle Pearce: You start to go, huh, there’s something going on here. And again, it’s like now you’re captivated and you’re drawn in. How do you plan what sort of tasks you might do? If a teacher is sitting at home listening to this going, “Wow, I’ve never heard of vertical non permanent, or maybe I have and I haven’t really understood how,” and they want to go try this, what are some things that you’re thinking about in order to select a task that might at least give me a good jumpstart on trying this in my own classroom?
Peter Liljedahl: Well, there’s two types of tasks that live in the thinking classroom. The one is what I call a rich task. Those are vital at the beginning part, and those are the ones we do in the workshops because coming in and doing a really exciting long division problem with a group of teachers isn’t really going to convey the message. For rich tasks, I look for a number of things, but we can use common lingo, low floor, high ceiling and things like this. What I really want is what I call evolving complexity. The further you get into the problem, the more complexities reveal themselves. Those evolving complexities are only accessed by the students who are getting through there as opposed to hitting them with complexity right out of the gate. These rich tasks … and I have a collection of them. It turns out we need them early on when we’re building the culture. We also refer to them as non curricular tasks because the goal is not to get through curriculum. There are some resources out there that allow you to teach an entire curriculum through rich tasks, and I really appreciate those, but it gets harder and harder to do the higher the grade goes.
Peter Liljedahl: What those tasks do, and when we’re introducing thinking classrooms to students is we start to get them into the habit of anticipating the next complexity, and stealing the next question from another group around them, and enjoying being in that space where we’re learning more, and more, and more, and the task is getting harder, and harder, and harder, and we’re up for the challenge, and this is fun. And I’m really enjoying doing the thinking, and the learning, and the meaning making. That’s the culture we’re trying to build. And at the same time, that it’s a safe space, it’s collaborative, there’s lots of visuals around the room and other groups working. There isn’t anyone focused on me. It’s a safe space to make mistakes because I can erase it because it’s a non permanent surface. It becomes a safe environment to start to forge ahead into this space.
Peter Liljedahl: And then we slide into what I call the more curricular based tasks, which really are just tasks that we normally do with our classroom. Coming in and asking our students to factor a trinomial without me having taught them how to do it. And then when they figure that one out, they get the next one, which is harder, and then the next one, which is harder yet, and the next one, which is harder yet. And so on and so forth. Everything is the same about this experience as with a rich task except what I’m doing now is I’m hitting the curriculum head on, but it still has all those pieces. It has evolving complexity as the coefficients change, and the signs on the coefficients change. It has the opportunity to make meaning at every stage. It has a low floor if you set it up right, and we can walk into this, and we can all be successful at this level. But it is going to get harder and harder.
Peter Liljedahl: My goal in thinking classrooms has always been not to build and find engaging tasks, but to build and engage students that can then be pointed-
Kyle Pearce: That’s a show notes quote right there.
Peter Liljedahl: And then you point those engaged students at any content, and they will think and engage, and make meaning, and engage in the evolving complexity. That’s what the game is here. That’s what the goal is.
Jon Orr: I think you addressed a lot of questions that Kyle and I wanted to chat with you about here today because when we talk about teaching this way through task and engaging our students the way you’ve articulated it, and especially bringing out some of the tasks that you share in your website, teachers will say, “Yeah, that’s all great, but when am I supposed to do that?” Or, “I have to cover curriculum. I have to teach the curriculum expectations.” I just want to summarize what you said for those teachers who have those kind of questions. You’re saying work with the non curriculum tasks first, which can help build that culture, build that community in your classroom. And then slowly move into the curriculum or the curricular tasks that help engage them in that learning process, and then it’s not such a shock when all of a sudden they’re learning new stuff, but they’ve already been experienced to this new way of engaging their own learning.
Jon Orr: Would that be your recommendation to teachers who are like, “I don’t have that kind of time to teach that way?” I hear that a lot, especially in high school for sure.
Peter Liljedahl: I hear it a lot too. You got to go slow to go fast. Taking that time early on to build the competencies, to build up the culture, to build the norms of the thinking classroom, and then pointing them out of the thinking classroom pays off in spades. The longest it takes to do a unit on factoring quadratics is two days. It usually takes one day. Completely the square is usually a one day unit. Log rhythms, we’ve gone through in as … well, that one takes two days usually, sometimes three. We’re tearing through content once we get the students thinking. When students are not thinking, everything we teach is difficult.
Kyle Pearce: Right, yeah, because they don’t understand anything. Because no learning is actually happening, and you’re just spinning tires.
Peter Liljedahl: We got to cut the content into bite size pieces, and pre chew it for them. Right?
Kyle Pearce: Right, right. It’s interesting because I’m sitting here, and there’s lots of head nodding. This is the one time that I wish that there was video on podcast because I’m sitting here, and you can’t see my acknowledgment and my agreeance going on. But a few things, even going back to this non curricular first idea to build that culture, it reminds me a lot of what Jon and I tend to suggest for teachers who haven’t used a Notice and Wonder in their classroom. We’re big on with curiosity, we like to push this idea of noticing and wondering, and really getting kids to again, think but in a very non threatening way. Early on, day one of the course, we sort of say the same thing which is, “Let’s just build the culture. We’ve got to do … and this is an investment. ” But then the other piece that I’m hearing from you as well is this idea of these non curriculum tasks might set off a red flag for a teacher. But at the end of the day in most curriculums, whether it’s a common core, or here in Ontario where Jon and I are from, we have the process expectations, which when you look at those, those are the curriculum.
Kyle Pearce: Same with these mathematical practices for common core, and I’m sure in may other curriculums around. It’s not all content based, and yet a lot of us sometimes just get hung up on that. And like you’re saying, by building that culture, we get that huge payoff later where now we get to focus on teaching where it matters, instead of teaching all the surface stuff where the kids are kind of peeling that stuff away really fast as they gain more confidence and engage in the culture in the classroom.
Peter Liljedahl: I had a master’s student named Maria [Kurkof 00:48:01]. She did her master’s thesis on the way the context was a thinking classroom. In a grade 10 curriculum in British Columbia, and in BC grade 10 is still common curriculum, so we have almost all the kids together in a grade 10 class. So 18 days, for four weeks straight, all she did was rich tasks. None of this, let’s point them at core content. Just rich tasks, she picked … And there was a couple of holidays in there, so it ended up being 18 school days. She did 18 rich tasks in 18 days, and she tracked a student to see how much math they bumped into during those 18 days. By math, I mean both curricular math and what we call the competencies, which is your processes. In 18 days, she bumped into every grade 10 learning outcome except for two. A whole bunch from grade 11 and grade 12, a whole bunch from grade 9, 8, 7, down to 6, and hit pretty much all of the competencies.
Peter Liljedahl: It was like, if we could just do rich tasks … and I really firmly believe in that, I would love to be able to do just rich tasks. But my goal is to make every task rich. What determines whether a task is rich has a lot more to do with the disposition of the student and the environment in which it’s done than it does the actual task. That’s what I’ve been working on.
Kyle Pearce: That’s awesome. I love how you use the term bumped into, because I find ourselves saying very similar things when we’re promoting this idea of trying to un-unitize or un-silo, or de-silo all of the curriculum and mix it up a little bit in order to promote more thinking and more problem solving those resilient problem solvers. It’s great to hear that echoed in that description there.
Jon Orr: Peter, we know you are a busy man, and we don’t want to take up too much of your time, but we have maybe just two more questions here. One that we’re probably going to be trying to ask all of our guests near the end of our episodes which is … just to give you a little background, in my class, I start each semester and end each semester with asking my students to complete a phrase which is, math is like … and then I just leave the dot, dot, dot. Their job is to complete that sentence. So what is it like, and then explain why they say that. What is helpful for me, it gets everything out into the open on the first day of class like where they’re coming from, some of the ideas that they bring with them, what are their thoughts on math. We have a good discussion about that to start setting our mindset. And then we end the semester … we just ended our semester the time of this recording, so I always bring it back to see if anybody has changed after being in my class for a semester.
Jon Orr: We want to pose that to you. So if I said math is like, and then dot, dot, dot, what would you say?
Peter Liljedahl: Okay, before I answer that question I have to tell you something that I do in my teaching. When I teach the undergraduates, the pre-service teachers, I always ask them four questions. I ask it to them on the first day, I ask it to them on the last day, and I ask it to them on a day in the middle. And the four questions are, what is mathematics? What does it mean to teach mathematics? What does it mean to learn mathematics? And did Peter teach today? Those are the four questions I get asked. I’ve actually written research papers on the results of that research, and how their views and their beliefs change over time. If you want to ask me what mathematics is. I’m going to say mathematics is a verb. I can come at that from lots of different perspectives, but mathematics is also a noun.
Peter Liljedahl: I think many of the problems that we’re faced with in math education today lives in the tension between math as a noun and math as a verb. Is math the stuff that we have to learn? Or is it the doing? Curriculum across candor are more and more moving into the math as a verb, and yet our external assessments is a lot about math as a noun. That’s the tension we live in. For me, the content of a curriculum is just the context. The processes or the competencies are the content.
Kyle Pearce: That to me is very powerful. I love those four questions as well. Just thinking about that, and I’m picturing especially question number four, if someone comes into your class, pre-service teacher, and you don’t say nearly as much as what I’m used to a teacher saying, I might have very different perspective on whether you taught anything that day or not. And then by the end, I’m certain that that would change quite dramatically. Peter, one more here. I just want to let you know we have a huge Google Doc here of questions. How silly of us to think that we were going to be able to dive into all 14 of the-
Jon Orr: I think we got through two.
Kyle Pearce: … of those recommendations. Yeah, we got through two. I’m hoping maybe sometime in the future we’ll be able to invite you back on, and dive into some of these others more deeply. But before we let you go, what are you working on right now? What’s keeping you curious in the teacher education space right now? Is there anything? Maybe it’s content focused? Maybe it’s a verb, or maybe it’s a noun? What’s on your mind currently?
Peter Liljedahl: Well right now, I’m writing up the book, Building Thinking Classrooms, so that’s keeping me busy and curious. I’m doing some research on tensions that teachers experience. One of my doctoral students is doing her thesis on that. I’m also spending some time with some international collaborators, looking at some creativity in mathematics, which was the basis of my PhD thesis. Sort of breaking down some of the barriers around creativity. That’s sort of the space that I’m living in right now, but what’s keeping me curious in the thinking classroom framework is I am gearing up to spend a lot more time thinking about how this framework applies in other subject areas. I’m still trying to understand why some things are the way they are in the thinking classroom framework.
Peter Liljedahl: I have a pretty good handle on the results of each of the pieces and why that is what it is. But the sequence of four toolkits of the 14 practices are embedding in is still fascinating me because that was an empirically emergent result, and trying to understand why some things are where they are in this sequence. There’s some new data that’s showing that maybe some of these are a little bit more flexible.
Kyle Pearce: I’m very excited to keep our ears to the ground. When your book comes out, I’m sure it’s going to be a very, very hot item out in the PD market for sure. Peter, thank you so much for joining us. It’s so great to hear. I know where you are right now, things are a little bit nicer. Not necessarily warm, but warmer than where Jon and I are right now. Thank you so much for joining us. We can’t wait to share this episode with the rest of the math community, and hopefully we’ll see you at a conference sometime soon.
Peter Liljedahl: Thank you for your time.
Jon Orr: Wow, thanks so much, Peter, for joining us on the Making Math Moments That Matter podcast. You dropped a bunch of math PD knowledge bombs on us during that interview.
Kyle Pearce: The biggest takeaway for me was how Peter suggested that teachers may want to consider starting with problems that are non curricular in nature in order to build that culture of thinking in the classroom, prior to building in the curricular focused tasks. It just goes to show how important building that culture in our classroom is, and it is an investment that’s going to reap huge rewards in the long run. Something for us all to keep front of mind. How about you, Jon? What resinated with you?
Jon Orr: Yeah, there was a ton of things, but my biggest take away was how he said that there are 14 recommendations for the work that he’s doing with the thinking classroom, and 100 ways to wreck it. It’s so important that we critically think about the things we say and do in our classrooms with students. I think gone are the days where I can just pull up an example or a problem and solve it, winging it without thinking about what questions I want to ask the students, and what language and actions I need to show them. It’s, I think, so important that we critically think about these things going forward. I’m looking forward to having him back on the show to talk more about that and other parts of that thinking classroom.
Kyle Pearce: Awesome stuff. How about you at home? What’s your big takeaway from this episode? Remember, you’ve got to share it with a friend. Maybe it’s a colleague. Or send us a message on social media at Make Math Moments on twitter, Instagram or Facebook.
Jon Orr: In order to ensure you don’t miss out on the new episodes as they come out each week, be sure to subscribe on iTunes or your favourite podcast platform.
Kyle Pearce: Also, if you’re liking what you’re hearing, please share the podcast with a colleague, and help us reach an even wider audience by leaving us a review on iTunes, and tweeting us @makemathmoments on twitter. Show notes and links to resources from this episode can be found at MakeMathMoments.com/episode21. Again, MakeMathMoments.com/episode21.
Kyle Pearce: Well, until next time, I’m Kyle Pearce.
Jon Orr: And I’m Jon Orr.
Kyle Pearce: Hi five’s for us.
Jon Orr: And high five’s for you.
6 Comments
Trackbacks/Pingbacks
- Grouping Students | Math With Ms. Tong - […] in British Columbia – on over 400 classrooms! If you don’t feel like reading a paper, listen to this…
- Make Math Moments 3-Part Framework: Spark Curiosity, Fuel Sense-Making, Ignite Teacher Moves - […] Liljedahl – our guest from episode 21 of the podcast – is one of many researchers who is exploring…
- Episode #53 - Open Middle Math: An Interview with Robert Kaplinsky - Make Math Moments - […] Episode 21: Peter Liljedahl […]
- Episode #50: How To Get High IMPACT PD FROM YOUR COUCH: The Make Math Moments Virtual Summit - Make Math Moments - […] Episode 21 – The Thinking Classroom […]
- Episode #39: Everyone Can Learn Math: An Interview with Alice Aspinall - Make Math Moments - […] Episode #21: The Thinking Classroom: An Interview with Peter Liljedahl […]
- Episode #52 The Purpose of Assessment: A Math Mentoring Moment - Make Math Moments - […] Episode 21 with Peter Liljedahl and Thinking Classrooms […]
- Episode #98: The Thinking Classroom Part 2: An interview with Peter Liljedahl - Make Math Moments - […] Episode 21: The Thinking Classroom: An Interview with Peter Lijedahl. […]
- Are your students mimicking or thinking? - MATH RECOVERY BLOG - […] https://makemathmoments.com/episode21/ […]

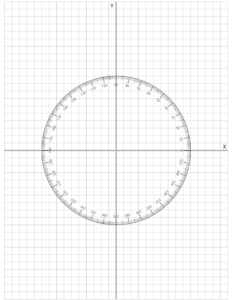

Great interview! I am familiar with Peter Liljedahl’s work and have implemented visible random groups and vertical non-permanent surfaces but every time I listen to him, I learn more! I like his quote about building engaged students so they can be successful with any math they face. I appreciate his suggestion about beginning with non-curriculum rich tasks to create a culture of learning and risk-taking and then move into curriculum tasks. I also like the 14 ways to help build thinking classrooms.
Thanks for popping by, Cathy! Isn’t it crazy how no matter how deeply we might know something, there is always more there. I felt the same way on the other end of the conversation despite having had heard Peter speak on a number of occasions as well as having conversations with him multiple times throughout the years. This is an episode I’ve relistened to a few times already.
Some questions for Peter, or the two of you. 1) My students will all be carrying a district issued Ipad next year. What place does a device like that have in the thinking classroom? 2) Is there a maximum number of students that can be engaged in the thinking classroom? Like, I will have 30 or more in my PreCalc classes. Is that too many? Or can that be manged by making the groups bigger than 3 students? 3) Peter recommends a visibly random group of 3 to work together for the day. What if you don’t reach a conclusion to your task/problem by the end of the class? Continue the next time with new groups or the same group? Thanks, Cary
Hi Cary,
1. My students have iPads too and we use them regularly to take pictures of our work, use Desmos, and use other math related apps.
2. I’ve had upwards of 30 students. Groups of 2 or 3 are ideal. You may have some students spill out into the hallway.
3. As for conclusions. Some lessons may stretch over days, but I try to ensure that the learning goal is brought forward before the end of class.
Please contact me on Whatsapp: 79697516322
Hello!
I am so eager to build a thinking classroom this year. I have utilized rich tasks in the past and where I am struggling is how to do this every day. I am in a state that utilizes high-stakes testing and I am wondering how to intervene with students who are not meeting the mastery of learning objectives. Do you use small groups? Do you differentiate the task? I plan on using mastery days like Mr. Orr, but how could I do that while still utilizing this framework